距离扩展目标检测中的强散射点自适应估计方法

孙迎丰，曾维贵，史 冲，王新政

（1.海军航空工程学院a.研究生管理大队；b.科研部，山东烟台264001；2.91206部队，山东青岛266108）

早期雷达分辨率较低，目标回波都集中在1～2个距离分辨单元内，目标被视为点目标。随着雷达分辨率的提高，目标回波分布到多个不同的距离分辨单元内，形成距离扩展目标。即使中低分辨率的雷达，对于舰船等大中型目标，雷达工作波长远小于目标尺寸，目标回波在距离维上同样表现出较强的扩展性。由于高分辨技术的广泛应用，距离扩展目标检测成为当前雷达信号处理领域中的研究热点。

有关距离扩展目标检测的理论研究有很多[1-9]，这些研究大多针对不同杂波背景下的检测器设计和检测性能分析。以上研究表明，对分布在多个距离单元上的目标回波进行有效的信息积累，可以提高距离扩展目标的检测性能。常用积累检测方法有能量积累检测和二进制积累检测。理论分析表明，能量积累检测可克服二进制积累检测的量化损失，其检测性能要优于后者；但是二进制积累检测的实现相对简单，实际应用更为广泛。

距离扩展目标检测中的积累主要是指脉冲内的非相干积累，即在空间上对多个距离单元的积累。常规的能量积累检测假设目标散射点占据整个目标窗口。然而，实际情况表明，即使是物理尺寸占据多个距离单元的目标，也可能只有很少几个单元有强散射点存在。目标强散射点稀疏分布的特性会造成检测性能下降，即存在陷落损失[10]。为克服陷落损失问题，现有研究多采用先提取目标强散射点，只对目标的强散射点进行积累的检测思路。本文正是以此为出发点，利用最大类间方差法对目标强散射点进行自适应估计，并以高斯背景下的距离扩展目标能量积累检测方法为例，通过仿真验证其改善检测性能的有效性。

1 目标强散射点估计方法

目标强散射点的分布情况是未知的，而且不同的目标存在很大差异，即使是对同一个目标，当目标相对于雷达的姿态发生变化时，目标回波中强散射点在各距离单元中的分布情况也有很大变化。因此，目标散射点的准确估计对提高距离扩展目标的检测性能具有实际意义。

由于雷达探测的距离范围远大于目标长度，因而在进行目标检测时，通常采用距离滑窗检测的方法进行分段处理。假定距离滑窗长度为N，回波采样信号x(n),n=1,2,…,N；目标回波窗口w=[K0,K0+L-1]，K0、L分别为目标窗口起始位置和窗口宽度。假设目标窗口之外的回波为噪声，定义平均信噪比为：

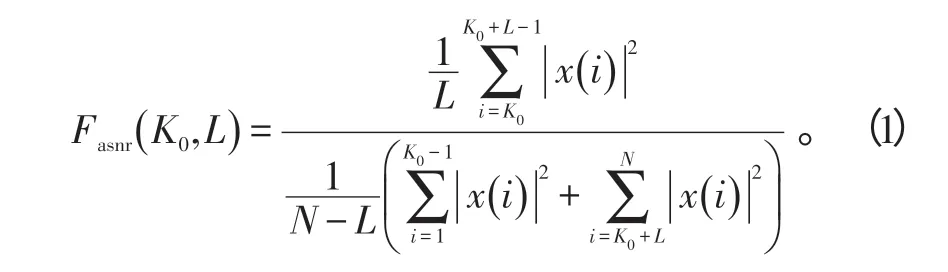
由于K0和L 未知，现有研究一般利用最大信噪比准则[11]估计目标窗口，并在此基础上获取目标强散射点，即

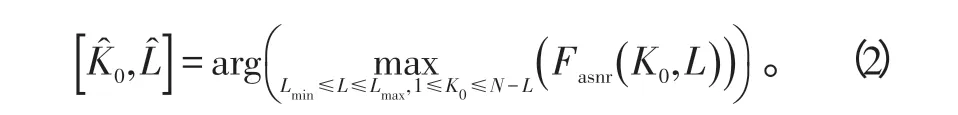
式（2）中：arg(·)为取变元操作；Lmin和Lmax分别为目标可能的最小长度和最大长度。

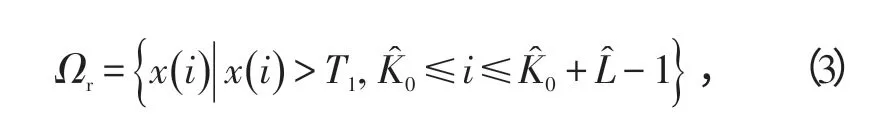
Ωr表示目标强散射点的集合，后续处理即对Ωr内的回波进行积累构造检测统计量。

文献[12]以滑窗内的平均功率与经验系数的乘积作为确定强散射点的门限。文献[8]根据经验系数设定第一虚警概率，进而确定强散射点的门限。显然，经验系数具有很强的随意性，检测性能随经验系数的变化较大。而且目标窗口的估计是二维的搜索优化过程，一般难以满足目标检测的实时性要求。文献[6]在将散射点幅度降序排列后，序贯积累散射点能量并与门限比较，其实质是穷举所有可能的散射点个数进行积累检测。其搜索过程与积累检测过程耦合紧密，当滑窗内不存在目标时，计算量反而更大。其他强散射点估计方法[2，10]，均存在计算复杂或检测性能不稳定的问题，实际应用受到限制。

本文采用最大类间方差法[13-14]对目标强散射点进行估计。该方法是利用目标和背景的特性差异，依据类间距离极大准则来确定区分目标和背景的门限。因其计算简单、自适应强，在图像处理领域应用广泛。本文在估计强散射点的处理过程中对该方法略有适应性改进，但处理的基本思想一致。

首先，对距离滑窗内的回波信号进行归一化处理得到x′(n)，n=1,2,…,N；然后，以T1为门限将回波采样分为2类，即背景杂波C0和目标回波C1：

2类的均值分别为：

式中，N0、N1分别为2类的样本数目。

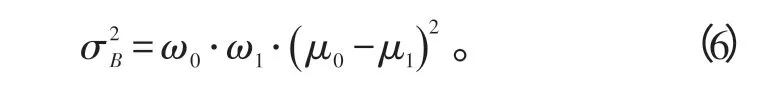
式（6）中：ω0+ω1=1；

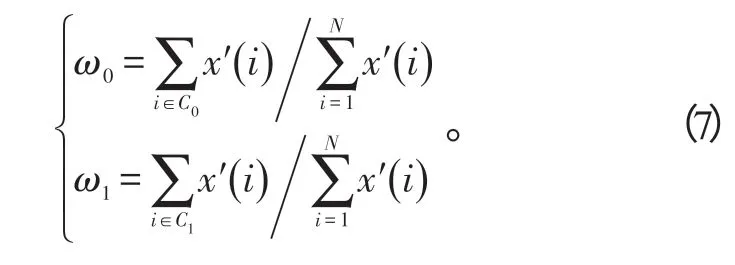
为便于解算，让T1在x′(n)内依次取值，使得类间方差σ2B最大的T1即为最佳门限：

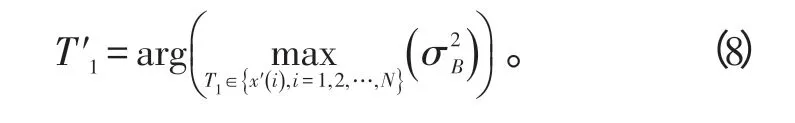
尽管该方法也需要搜索参数空间以获取最佳门限，但是该方法只进行一维搜索，而且通过设计搜索优化方法可满足快速求解的需要。在得到门限T′1后，比较容易确定强散射点，再根据目标尺寸的先验信息进行简单搜索即可获得目标回波窗口，并最终确定目标强散射点的集合。

2 距离扩展目标能量积累检测

假设目标有K个强散射点，目标回波占据L个距离单元，1≤K≤L，相应的检测模型为：

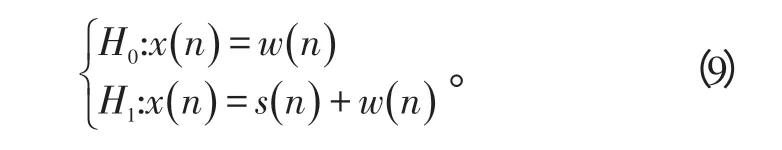
根据Neyman-Pearson准则，距离扩展目标能量积累检测方法的检测统计量为

H0假设下，Λ 服从自由度为2L的χ2分布，其概率密度函数为

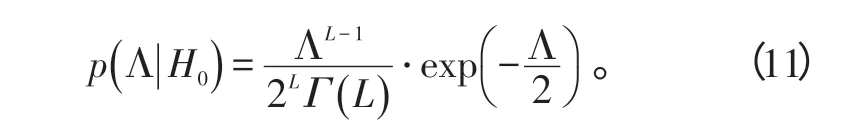
H1假设下，Λ 服从非中心参数为λ、自由度为2L的非中心χ2分布，其概率密度函数为

虚警概率和检测概率分别为：

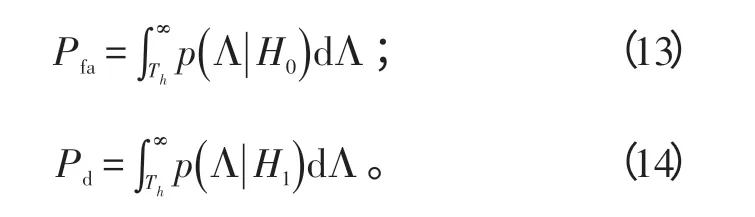
式（13）、（14）中，Th为检测门限。

易知，对于给定的虚警概率Pfa，目标窗口宽度L越大，门限Th越高；检测概率Pd取决于信噪比和目标窗口宽度L。当散射点K 一定时，即给定信噪比条件下，L 越大，Pd越小。因此，只有把K个散射中心所在的距离分辨单元的信号能量积累起来，才能获得最优的检测性能。所以，最优积累的检测统计量为

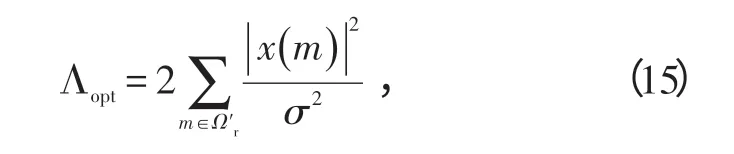
式（15）中，Ω′r表示目标的K个散射中心的集合。

一般而言，Ω′r是无法完全获取的，只能对其进行估计。也就是说，最优积累检测是无法实现的，只能作为检测器性能分析和评估时的参照基准。

3 检测性能仿真分析

由于强散射点估计方法中涉及运算较为复杂，难以给出虚警概率或检测概率的解析式，一般采用Monte-Carlo仿真方法进行性能分析。为充分考察强散射点自适应估计方法的有效性，本文将其与全窗积累检测法（检测统计量由式（10）描述，方法1）、最优积累检测法（检测统计量由式（15）描述，方法2）、文献[8]提出的积累检测法（方法3）进行仿真性能比较，本文的自适应积累检测法为方法4。

仿真中假定噪声的方差已知，不失一般性取σ2=1，通过改变总的目标回波功率来调节信噪比的变化，信噪比定义为目标回波总能量与噪声功率之比。假设距离滑窗宽度N=60，目标强散射数目K=5，各散射点的强度为[1/25，3/25，5/25，7/25，9/25]，强度数值表示各个散射点占目标总能量的比重。目标窗口宽度L ＞K，仿真实验中各散射点随机分布在目标窗口内，用于模拟不同的散射点稀疏分布情况。

仿真结果如图1所示。从图1中可以看出，在目标稀疏分布的情况下，全窗积累法较最优积累法存在性能损失，而且在K 一定时，L 越大，陷落损失越大，即检测性能下降越严重。而方法3及本文所提方法4通过强散射点估计和积累可有效地改善陷落损失，提高检测性能。

另外，图1表明方法4的检测性能略优于方法3，但是改进效果并不明显。对此，本文进一步对其进行分析。方法3是通过第一虚警概率Pfa1计算门限并提取强散射点，其中Pfa1=，a为经验系数，图1中a=1.5。

图2所示为Pfa=10-4，L=15时，不同a值情况下的检测曲线。

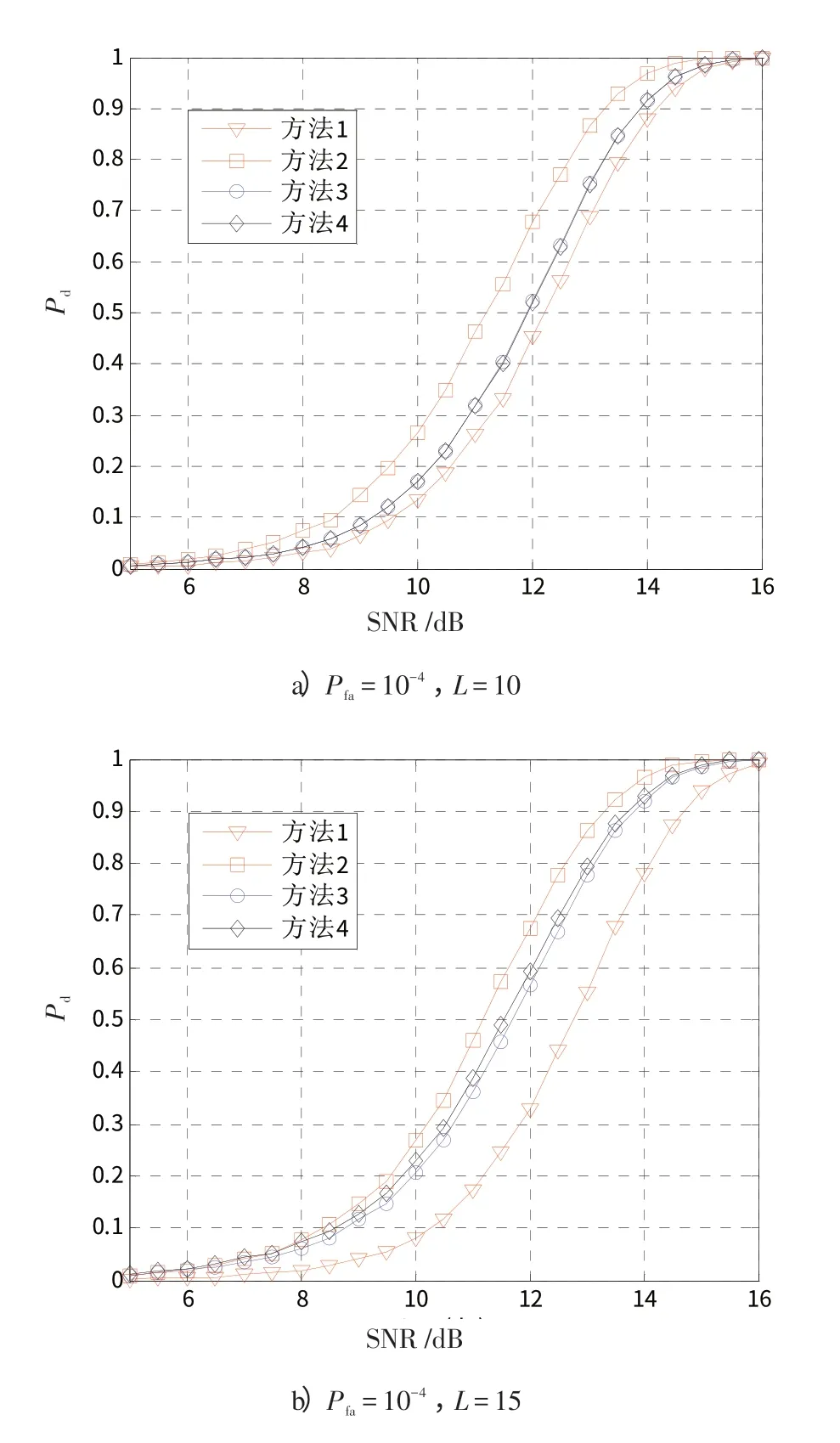
图1 不同积累方法的检测性能曲线Fig.1 Detection performance for different methods

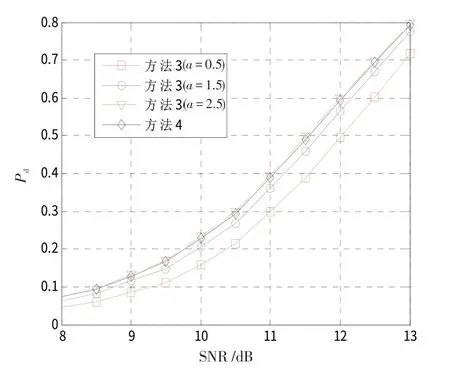
图2 方法3与方法4的性能比较Fig.2 Detection performance of method 3 vs method 4

由图2可以看出，a的取值会影响检测性能。经分析可知，对于给定的L、a值越大，Pfa1越高，对应的提取强散射点的门限越低，参与积累的散射点越多。然而，积累的散射点并不是越多越好，引入噪声反而会降低检测性能。而且考虑到不同的检测背景，a的取值将更为复杂。由此可见，相较于方法3，方法4对强散射点进行自适应估计，能避免因经验系数带来的影响，具有更好的鲁棒性。

4 结束语

本文提出了基于最大类间方差的目标强散射点估计方法。相较于其他估计方法，该方法具有计算简单、自适应性强的特点，并通过仿真验证了该方法提高距离扩展目标检测性能的有效性，为实现简单实用的距离扩展目标检测器设计提供了一种新思路。

[1]简涛，何友，苏峰，等.高距离分辨率雷达目标检测研究现状与进展[J].宇航学报，2010，31（12）：2623-2628.

JIAN TAO，HE YOU，SU FENG，et al.Overview of high range resolution radar target detection[J].Journal of Astronautics，2010，31（12）：2623-2628.（in Chinese）

[2]陈新亮，王丽，柳树林，等.高分辨雷达扩展目标检测算法研究[J].中国科学：信息科学，2012，42（8）：1007-1018.

CHEN XINLIANG，WANG LI，LIU SHULIN，et al.Research on extended target detection for high resolution radar[J].Science China：Information Science，2012，42（8）：1007-1018.（in Chinese）

[3]孟祥伟，曲东才，何友.高斯背景下距离扩展目标的恒虚警率检测[J].系统工程与电子技术，2005，27（6）：1012-1015.

MENG XIANGWEI，QU DONGCAI，HE YOU.CFAR detection for range extended target in Gaussian background[J].Systems Engineering and Electronics，2005，27（6）：1012-1015.（in Chinese）

[4]顾新锋，简涛，何友，等.非高斯杂波背景中的两个距离扩展目标检测器[J].宇航学报，2012，33（5）：648-654.

GU XINFENG，JIAN TAO，HE YOU，et al.Two detectors of range-spread target in non-gaussian clutter[J].Journal of Astronautics，2012，33（5）：648-654.（in Chinese）

[5]CONTE ERNESTO，DE MAIO ANTONIO，RICCI GIUSEPPE.GLRT-based adaption detection algorithms for range-spread targets[J].IEEE Transactions on Signal Processing，2001，49（7）：1336-1348.

[6]戴奉周，刘宏伟，吴顺君.一种基于顺序统计量的距离扩展目标检测器[J].电子与信息学报，2009，31（10）：2488-2492.

DAI FENGZHOU，LIU HONGWEI，WU SHUNJUN.Order- statistic- based detector for range spread target[J].Journal of Electronics &Information Technology，2009，31（10）：2488-2492.（in Chinese）

[7]顾新锋，简涛，何友，等.一种基于散射中心密度的距离扩展目标检测方法[J].信号处理，2009，12（25）：1941-1945.

GU XINFENG，JIAN TAO，HE YOU，et al.A detection method based on scattering density for a range-spread target[J].Signal Processing，2009，12（25）：1941-1945.（in Chinese）

[8]顾新峰，简涛，苏峰，等.一种基于强散射中心的距离扩展目标检测方法[J].数据采集与处理，2009，24（5）：576-580.

GU XINFENG，JIAN TAO，SU FENG，et al.Spatially distributed target detector based on scatterer[J].Journal of Data Acquisition&Processing，2009，24（5）：576-580.（in Chinese）

[9]张晓利，黄勇，关键，等.基于距离单元选择的距离扩展目标检测器[J].系统工程与电子技术，2012（1）：69-74.

ZHANG XIAOLI，HUANG YONG，GUAN JIAN，et al.Range-spread target detectors based on range-cell-selecting[J].Systems Engineering and Electronics，2012（1）：69-74.（in Chinese）

[10]陈远征，赵宏钟，付强.扩展目标检测的陷落损失问题与改进方法[J].雷达科学与技术，2010（3）：258-263.

CHEN YUANZHENG，ZHAO HONGZHONG，FU QIANG.Problem of collapsing loss and improved method for detection of range spread targets[J].Radar Science and Technology，2010（3）：258-263.（in Chinese）

[11]孙文峰，何松华，郭桂蓉，等.自适应距离单元积累检测法及其应用[J].电子学报，1999，27（2）：111-112.

SUN WENFENG，HE SONGHUA，GUO GUIRONG，et al.Adaptive range-cell integrated detection method with application[J].Acta Electronica Sinica，1999，27（2）：111-112.（in Chinese）

[12]胡文明，关键，何友.基于视频积累的距离扩展目标检测[J].火控雷达技术，2006，35（4）：16-18.

HU WENMING，GUAN JIAN，HE YOU.Range extension target detection based on video frequency accumulation[J].Fire Control Radar Technology，2006，35（4）：16-18.（in Chinese）

[13]NOBUYUKI OTSU.A threshold selection method from gray-level histograms[J].IEEE Transactions on Systems Man and Cybernetics，1979，9（1）：62-66.

[14]EIDAH ASSIDAN，ALI EL ZAART.Fast optimal multimodal thresholding based on between-class variance using a mixture of gamma distributions[C]//IEEE International Conference on Systems，Man and Cybernetics.2009：2599-2602.