基于倒谱的运动模糊图像参数估计方法

（海军航空工程学院基础部，山东烟台264001）

图像在形成、传输和存储的过程中，由于受多种因素的影响，图像的质量会有所下降，这一过程称为图像的退化或降质。如果想提取图像中的有用信息，就需要对退化图像进行复原。图像复原是研究怎样从退化的图像中复原出原始的清晰图像，也就是要根据已有的退化图像和估计的退化因子反演推导出原始的图像。退化因子即是需要估计退化过程的点扩展函数（Point Spread Function，PSF）。对于运动模糊退化，需要估计出运动模糊PSF 中的2个参数——模糊尺度和模糊方向。

运动模糊参数估计主要有2类方法：一类是基于空域的参数估计方法[1-5]；一类是基于频域的参数估计方法[6-9]。基于空域的参数识别方法利用退化图像中的点、线和边缘等信息，当模糊尺度较大时，识别的误差也很大[4]。而基于频域的参数识别的方法受噪声影响严重[8，10]。

本文分析了运动模糊PSF的倒谱特性，得到基于倒谱的参数估计方法。并通过数值实验验证该方法的有效性。

1 运动模糊退化的数学模型

图像退化的一般模型可表示为[11]

式（1）中：g(x,y)、f(x,y)和h(x,y)分别为退化图像、原始图像和退化系统的PSF；n(x,y)表示噪声。不同的退化系统对应着不同的h(x,y)。

用摄像机获取景物图像时，由于相机曝光时景物和摄像机之间有相对运动而形成图像模糊现象称为运动模糊。运动模糊的PSF可以表示为：

式中，θ为模糊方向与x轴夹角。

如式（2）所示，运动模糊PSF依赖于2个参数——模糊尺度L 和模糊方向θ，因而对运动模糊PSF的估计就是对这2个参数进行估计。其傅里叶变换结果H(u,v)为

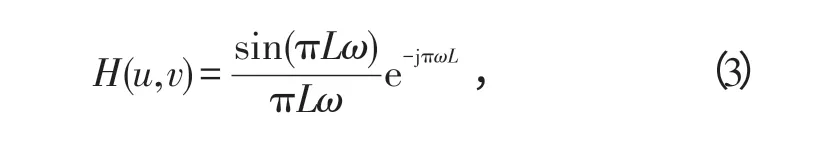
式中，ω=u cos θ+v sin θ。

2 倒谱定义及性质

给定二维函数h(x,y)，其倒谱的计算公式为[6]

式中，ℱ表示傅里叶变换。

倒谱可以看做从h(x,y)到C(p,q)的变换，如果用C{·}来表示倒谱变换，则

由于二维傅里叶变换ℱ是可分的[11]（即对二维函数f(x,y)做ℱ变换，可先对x（或y）做ℱ变换，再对y（或x）做ℱ变换）以及式（5）中绝对值的存在，算子C{·}为非线性可分算子。由ℱ变换的性质很容易推导出倒谱变换的性质：

1）旋转。如果C{h(r,θ)}=C(ρ,φ)，则

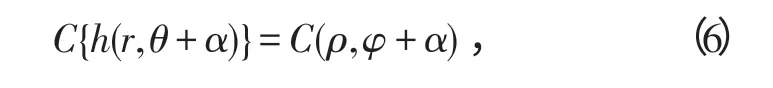
即函数旋转，倒谱也随之旋转，且旋转的角度值相同。

2）平移。因为

所以

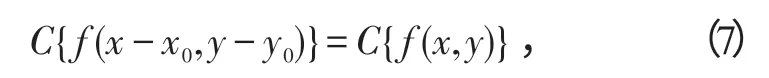
即原函数经平移后的倒谱与原函数的倒谱相同。

3）可分函数的倒谱。倒谱算子C{·}的一个重要性质为它的分离特性（对可分函数），下面进行分析。假设h(x,y)为可分函数，即

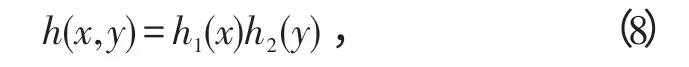
则h(x,y)二维ℱ变换可转化为对h1(x)和h2(y)的一维ℱ变换。记：

则

从而，

函数1(t)表示对所有的自变量t，函数值都为1。最后，做ℱ-1变换得

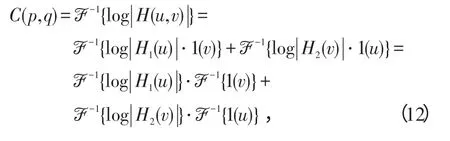
即

倒谱算子C{·}的分离特性来自于ℱ-1{1(t)}。由ℱ变换可知ℱ-1{1(u)}=δ(p)，ℱ-1{1(v)}=δ(q)，因而等式可改写为

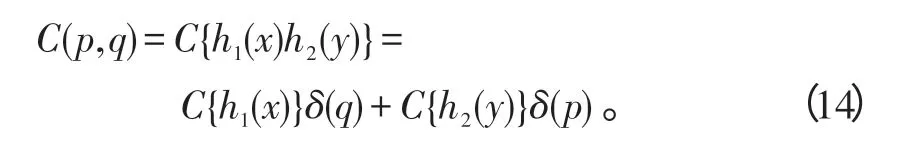
这说明可分函数的倒谱只出现在倒谱域的坐标轴（p=0，q=0）上，与x相关部分出现在p轴上，与y相关部分出现在q轴上。

综合以上3条性质可得：分析可分函数的倒谱时，只须通过函数在倒谱域坐标轴上的倒谱值和坐标轴的旋转角度即可。

3 基于倒谱特性的参数估计

由式（2），运动模糊PSF为常值函数，显然为变量可分离函数。可以通过倒谱域的坐标轴上图像可分析出运动运动模糊PSF中的参数信息。

在忽略噪声的情况下，根据式（1），有

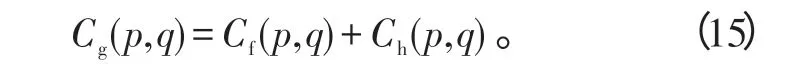
这样，模糊图像在时域为原图像和模糊核的卷积，变换到倒谱域之后为原图像的倒谱与PSF的倒谱之和。空间域的卷积在倒谱域变成了加法，可以比较容易地分离出模糊信息。为使H(u,v)=0时式（4）有意义，实际应用中图像的倒谱通常用下式计算[12]：

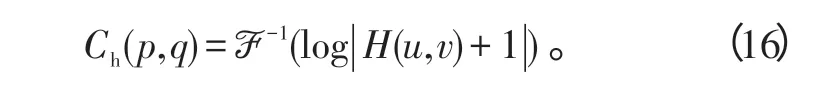
图1以lena图像为例，给出了原始图像的倒谱，运动模糊方向45°，模糊尺度为20个像素时的PSF的倒谱，以及运动模糊图像的倒谱。从图1b）中可以看出，原始图像的倒谱比较复杂，除中心亮点外，其能量分布均匀；图1c）中，PSF的倒谱在延模糊方向（45°）上出现周期性亮点；第一个亮点到中心的距离为20，意味着模糊尺度为20 像素，到中心的距离为40 像素处的第二个亮点为第一个谐波，谐波的产生是由于数值计算采用离散ℱ变换（DFT）造成的；图1d）中，模糊图像的倒谱为原图像倒谱与PSF的倒谱之和，由于原始图像的倒谱值集中在中心点附近（低频区域），故模糊图像的倒谱特征与PSF的倒谱特征相似，在沿模糊方向（45°）上出现周期性亮点。所以，可利用模糊图像的倒谱特征估计模糊参数。

图1 PSF与模糊图像的倒谱Fig.1 Cepstrem of PSF and blurred image

Radon变换[11]用来计算二维图像矩阵在某个方向上的投影，定义如下：

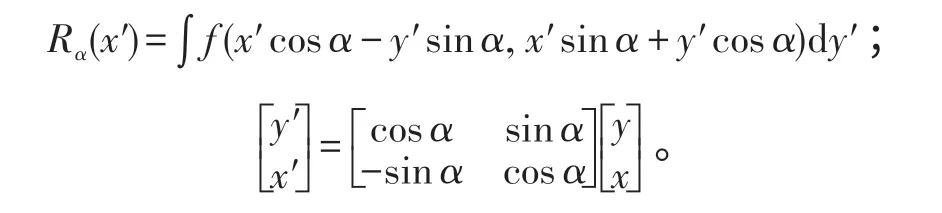
该投影即是在某一方向的线积分，反映了图像在不同方向上的投影性质。Radon变换一个重要的性质就是检测图像中的直线的方向，可以用Radon变换精确地检测出亮条纹的方向。若Radon变换中沿某个方向上的积分很大，则表明在与该方向垂直的方向上存在直线。图2给出了Radon变换检测直线方向的结果。当直线与水平方向成45°时，Radon变换的最大值出现在135°方向，与直线方向垂直。

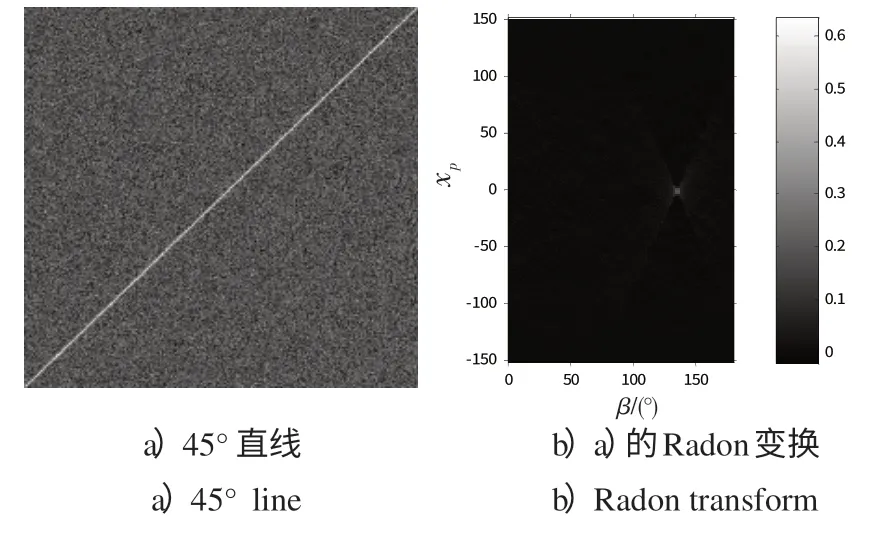
图2 Radon变换结果Fig.2 Results of Radon transform

综上，基于倒谱特性的参数估计方法如下：

1）运动模糊图像的倒谱在其模糊方向上有不断衰减的周期性亮点出现，其中离中心最近的亮点到中心的距离等于运动模糊尺度L[6]。

2）对于模糊方向θ的估计，可利用Radon变换。记α为找到变换结果最大值出现的方向，则运动模糊的方向θ=α-90°。

至此，PSF 中的运动模糊尺度L 和模糊方向θ 已全部估计出来。

4 数值实验

下面通过数值实验检验该方法的准确性和抗噪声干扰能力。

图3为基于倒谱的模糊方向检测结果，图3a）为原始lena图像，对图3a）施加方向为45°、尺度为20像素的运动模糊得到图3b）。运动模糊图像的倒谱如图3c）所示，对图3c）进行二值化处理得图3d）。图3e）是对图3d）进行Radon变换的结果，图3f）为图3e）的极大值曲线，从图3f）中可以看出Radon变换的最大值出现在135°方向，所以运动模糊方向为135°-90°=45°。

图3 基于倒谱的模糊方向检测Fig.3 Detection of blur direction

接下来估计模糊尺度。对于这种任意模糊方向的模糊，一般先将运动模糊方向旋转至水平方向，然后在水平方向估计模糊尺度，这样方便进行模糊尺度的估计。

图4为基于倒谱的模糊尺度检测的结果。将倒谱（图3c））顺时针旋45°，使其变成在水平方向上的运动模糊得到图4a）。由于倒谱具有中心对称性，可以只考虑右半部分，由中心到第一个亮点的距离为运动模糊距离L。提取出图4a）中的亮条纹如图4b），第一个亮点（坐标为204）到中心点（坐标为183）的距离为L=204-183=21个像素，与真实值的误差为1个像素。

图4 基于倒谱的模糊尺度检测Fig.4 Detection of blur scale

当加入均值为0、方差为25的高斯噪声时，模糊尺度固定为20个像素，模糊方向变化范围在0°～180°，对于模糊方向的检测结果如表1所示。相同的噪声条件下，运动模糊方向固定为45°，模糊尺度变化范围为5～20个像素，对于模糊尺度的检测结果如表2所示。从表1、2中可以看出，模糊尺度的检测误差在1°内，模糊尺度的检测误差在2个像素内，精度很高，证明该方法具有较强的鲁棒性。

表1 模糊方向检测结果（L=20）Tab.1 Detection results of blur direction（L=20）

表2 模糊尺度检测结果（θ=45°）Tab.2 Detection results of blur scale（θ=45°）

5 结论

本文提出了基于倒谱的运动模糊参数估计方法。首先，分析了运动模糊点扩展函数的倒谱性质，得出运动模糊图像的倒谱会在模糊方向上出现峰值，实验结果验证了理论分析的准确性。接下来，提出基于倒谱的参数估计方法，利用Radon变换检测出亮条纹的方向即是运动模糊的方向，第1个亮条纹与中心的距离即是模糊的长度。最后，通过数值实验验证了该方法的准确性和鲁棒性。

在估计模糊尺度时，本文采用的方法是测量中心到右侧第一个亮条纹的距离为模糊尺度。事实上，各个亮条纹之间的距离是相等的，都等于模糊尺度。下一步可以采取测量多个亮条纹之间的距离取平均的方法来进一步提高模糊尺度的估计精度。

[1]ARASHLOO SR，AHMADYFARD A.Fine estimation of blur parmeters for image restoration[C]//15th International Conference on Digital Signal Processing.2007：427-430.

[2]CHALMOND B.PSF estimation for image deblurring[J].Graphical Models and Image Processing，1991，53（4）：364-372.

[3]YITZHAKY Y，KOPEIKA NS.Identification of blur parameters from motion-blurred images[J].Graphical Models and Image Processing，1997，59（5）：310-320.

[4]WU S，LIN W，XIE S，et al.Blind blur assessment for vision-based applications[J].Journal of Visual Communication and Image Representation，2009，20（4）：231-41.

[5]KIM SK，PARK SR，PAIK JK.Simultaneous out-of-focus blur estimation and restoration for digital auto-focusing system[J].IEEE Transactions on Consumer Electronics，1998，44（3）：1071-5.

[6]ROM R.On the cepstrum of two-dimensional functions[J].IEEE Transactions on Information Theory，1975，21（2）：214-7.

[7]CANNON M.Blind deconvolution of spatially invariant image blurs with phase[J].IEEE Transactions on Acoustics，Speech and Signal Processing，1976，24（1）：58-63.

[8]KUNDUR D，HATZINAKOS D.Blind image deconvolution[J].Signal Processing Magazine，1996，13（3）：43-64.

[9]KANG X，PENG Q，THOMAS G，et al.Blind image restoration using the cepstrum method[C]//Canadian Conference on Electrical and Computer Engineering.2006：1952-1955.

[10]FABIAN R，MALAH D.Robust identification of motion and out-of-focus blur parameters from blurred and noisy images[J].Graphical Models and Image Processing，1991，53（5）：403-12.

[11]RAFAEL C GONZALEZ，RICHARD E WOODS.数字图像处理[M].3版.北京：电子工业出版社，2007：232-235.

RAFAEL C GONZALEZ，RICHARD E WOODS.Digital image processing[M].3rd ed.Publishing House of Electronics Industry，2007：232-235.（in Chinese）

[12]WU S，LU Z，ONG EP，et al.Blind image blur identification in cepstrum domain[C]//Proceedings of 16th International Conference on Computer Communications and Networks.2007：1166-1171.