基于动态广义费用的轨道交通客流划分模型研究

伍拾煤 裴玉龙 程国柱

（哈尔滨工业大学交通科学与工程学院，150090，哈尔滨∥第一作者，高级工程师）

基于动态广义费用的轨道交通客流划分模型研究

伍拾煤 裴玉龙 程国柱

（哈尔滨工业大学交通科学与工程学院，150090，哈尔滨∥第一作者，高级工程师）

根据轨道交通出行受运营时间影响较大的特点，基于旅客理想出行时间与实际出行时间之差所产生的动态广义费用，构建了不同收入水平旅客总广义费用最少与轨道交通运营部门票价收入最高的双目标优化模型。应用该模型分析了东莞—广州的客流，其结果符合东莞—广州的轨道交通发展趋势，证明了所构建模型的可行性及合理性。

轨道交通；客流；动态广义费用；双目标优化模型

First-author’s addressSchool of Transportation Science and Engineering，Harbin Institute of Technology，150090，Harbin China

近几年是我国轨道交通快速发展的时期，在短时间内建设了规模较大的高速铁路和城际轨道交通系统。但是，在各种轨道交通模式如何协调发展方面，缺少一种可行、可靠的分析方法。本文提出了一种基于动态广义费用的城际轨道交通客流内部划分模型。该模型是在城际轨道交通体系总分担率已经确定的情况下，在轨道交通系统内部再次进行划分。

1 多模式下的轨道交通系统“供需”博弈

为对多模式下的轨道交通系统的“供-需”博弈进行分析，本文引入广义费用概念。即：出行者根据自身需求，在选择交通方式时，将综合考虑各种轨道交通方式的票价、行程时间和舒适性等因素，作出最合适、最经济的选择。“供-需”博弈分析如下：

首先，按照“理性经济人”假设，出行者会对客运产品进行排序，选择自身效益最高即广义费用最低的方式出行［1］。轨道交通运营部门根据旅客的基于广义费用的出行选择行为，进行资源、运输策略和运输方案的调整，所有可行的运输方案的集合就构成了轨道交通运营部门在运输市场中的博弈策略集。而这种策略的实施又会影响旅客的出行选择。由此可见，轨道交通运营部门与乘客之间的博弈可被看作是斯坦克尔伯格博弈［2］。

2 多模式下轨道交通的出行广义费用

2.1 出行方式效用模型

轨道交通为旅客提供服务的水平主要由服务的经济性、快速性、舒适性、安全性等要素决定。旅客需要结合自身的经济条件，对这些要素进行权衡，进而选择不同的轨道交通模式。出行者一般以出行费用最低或者出行效用最大作为出行决策的基础。本文采用经济学中的效用原理，建立了计算不同轨道交通模式广义费用的模型。出行者在各项费用信息的获取方面存在不对称性，会出现高估或低判某类因素的现象，因此，需要根据旅客出行意愿的调查结果，对广义费用的计算结果进行修正、分析［3］。

由于各种轨道交通模式的安全水平相近，因此，本文的效用因素主要考虑经济性、快速性和便利性等3个服务特性，其效用函数计算公式为：

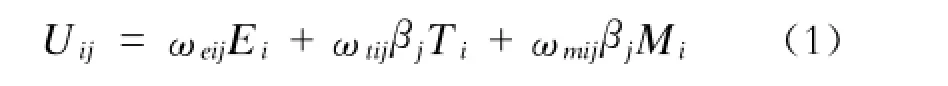
式中：

Uij——第i种轨道交通模式、第j类收入人群的广义费用，元；

Ei——第i种轨道交通模式的票价，元；

Ti——第i种轨道交通模式的旅行时间，h；

Mi——第i种轨道交通模式的便利性换算时间标度值，h；

βj——第j类收入人群时间转换费用系数，可用时间价值表示，元/h；

ωeij，ωtij，ωmij——分别为第i种轨道交通模式、第j种收入人群对Ei、Ti、Mi的修正权重。

各要素的取值或计算方式如下：

（1）经济性：把Ei作为经济性的衡量指标。各种轨道交通模式的Ei取标准票价，不考虑打折等因素。一般同等距离情况下，票价与列车的运行速度成正比关系，较高票价对应较高的运行速度。

（2）快速性：列车运行速度是体现各种轨道交通模式服务质量的基本特征之一。对于旅客来说，快速性是通过Ti来衡量的。

（3）便利性：便利性是通过时间来衡量的，主要包括旅客在市区内交通、购买车票、候车进站等环节所需的时间。计算公式如式（2）。

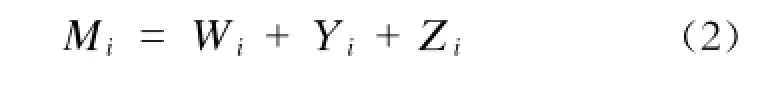
式中：

Mi——便利性的时间标度值，h；

Wi——第i种轨道交通模式成功购票平均所需时间，h；

Yi——第i种轨道交通模式平均候车排队进站所需的时间，h；

Zi——乘坐市区内交通到达第i种轨道交通模式的客运站所需平均时间，h。

2.2 异质出行者时间价值

旅客的时间价值可以客观地反映旅客旅行中所耗费时间的机会成本，或旅客对旅行时间节省的支付意愿，它实质上反映了人类社会经济活动中的时间效率。旅客的时间价值可以涵盖许多影响旅客决策的因素，成为影响旅客决策的主要指标。

计算各种轨道交通模式效用的核心问题是时间价值的计算，一般采用两种计算方法：一种是直接计算法，常用的有生产法、工资法（收入法）以及收入费用法等；另一种是间接计算法，通过对出行者出行行为进行统计或调查的数据来推算时间价值。本文采用的是直接计算法。由于可以得到用户的具体信息，故采用工资法。时间价值TV可按其收入水平和其认为的创造价值时间计算［1］：

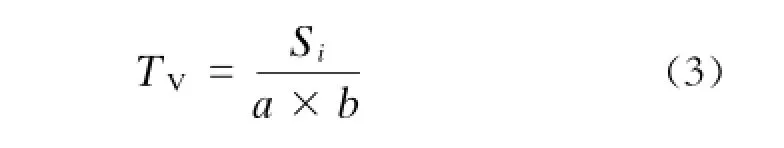
式中：

Si——通过市场调查得到的旅客月收入，元；

a——月工作天数，按22 d计算；

b——每日工作时间，按8 h计算。

2.3 基于熵权法的出行选择影响因素权重指标确定

熵权理论是一种客观赋权方法。在确定不同收入人群对出行选择影响因素的权重时，通过对熵的计算确定权重，即根据各项因素指标值的差异程度确定各因素的权重。熵值较小，说明该指标提供的有效信息量较大，其权重也应较大；熵值较大，说明该指标提供的信息量较小，其权重也应较小。当各被评价对象在某项指标上的值完全相同时，熵值达到最大。这意味着该指标未向决策提供任何有用的信息，可以考虑从评价指标体系中去除［4-5］。

熵权法确定权重的过程如下：

（1）原始数据矩阵标准化。m个评价指标，n个评价对象得到的原始数据矩阵为：

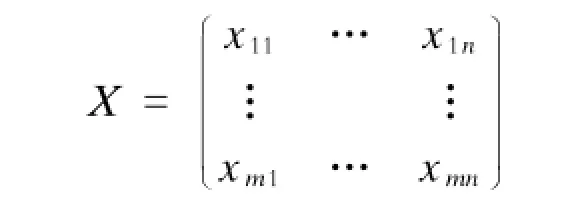
对该矩阵进行标准化得：

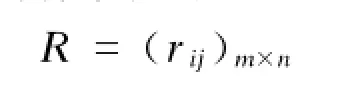
式中rij为第j个评价对象在第i个评价指标上的标准值，rij∈［0，1］。其中对大者为优的收益性指标而言，有：

（2）定义熵。在有m个指标、n个被评价对象的问题中，第i（i=1，2，…，m）个指标的熵定义为：

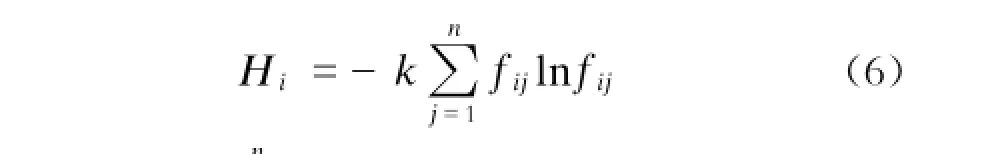
fij=rij/∑ rij，k=1/ln n，当fij=0时，

j=1令fijln fij=0。

（3）定义熵权。定义了第i（i=1，2，…，m）个指标的熵之后，可以得到第i个指标的熵权定义，即：

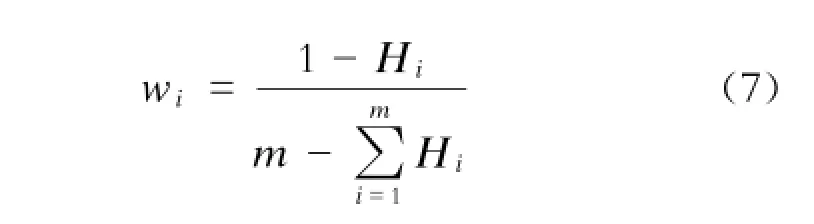
3 基于动态广义费用的目标优化模型

3.1 模型建立思路

20世纪70年代以来，在客运运输方式选择上，非集计模型一直是研究热点，且大部分研究偏重于城市内部交通［6］。区域交通系统是经济、技术、社会和政治等因素交叉在一起的复杂系统，由于对外出行旅客出行行为研究所需的数据复杂性和获取难度相比城市内部出行行为数据难度高，复杂、高深的数学工具很难解决其实际问题［7-8］。因此，一些运筹学专家提出，应采用“软系统”思考方法，如将过分理想化的“最优解”换成“满意解”，模型建立上应考虑决策者的正确判断以解决实际问题。本文的模型建立也遵循这一思想。

轨道交通票价由有关政府部门制定，不可随意调整。相比之下，运营时间有较大的灵活性。因此，运营部门可通过调整各时间段的运力，将其作为决策变量，在实现盈利最高的目的的同时，尽量降低旅客的广义出行费用。相比其他交通方式，轨道交通受运营时间的影响较大，当旅客的理想出行时间段与实际出行时间段发生冲突时，旅客会权衡自己的广义费用，当实际出行广义费用高于某个值时，旅客会选择其他交通方式或放弃出行。根据斯坦克尔伯格博弈思想，轨道交通运营部门在了解旅客的这些行为的前提下，首先判断旅客能够接受的广义费用值，然后据此合理安排各时间段的运力，保证客流量的同时使利益最大化。

3.2 考虑旅客动态时间费用的模型构建

根据以上思路，建立数学模型如下：

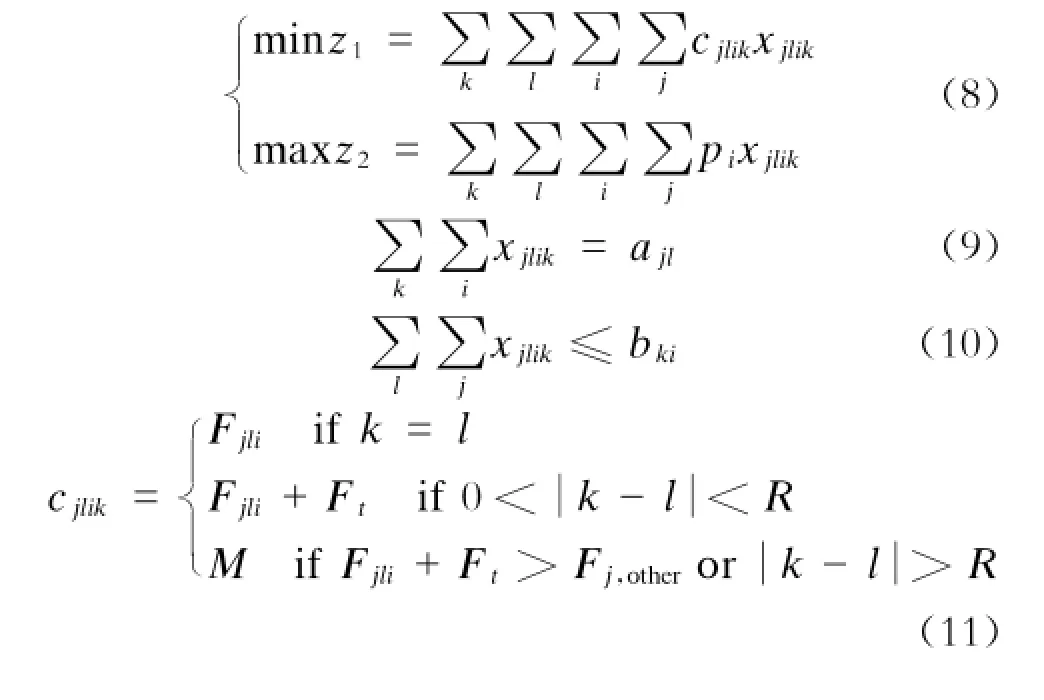
式（8）~（12）中：

xjlik——j类收入水平以l时间段为理想出行时间的旅客乘坐第i种轨道交通模式在第k时间段出行的出行量，人次；

pi——第i种轨道交通模式的价格，元/人次；

cjlik——j类收入水平以l时间段为理想出行时间的旅客乘坐第i种轨道交通模式在第k时间段出行的出行广义费用，元/人次；

ajl——j类收入水平以l时间段为理想出行时间的乘客数量，人次；

bki——k时间段第i种轨道交通模式的客运能力，为轨道交通部门决策变量，人次；

Fjli——j类收入水平以l时间段为理想出行时间的旅客乘坐第i种轨道交通模式在第l时间段出行的出行广义费用，元/人次；

Ft——j类收入水平以l时间段为理想出行时间的旅客在第k时间段出行时增加的广义费用，元/人次；

Fj，other——j类收入水平乘坐轨道交通出行方式之外的其他交通方式的广义费用，元/人次；

R——旅客所能接受的实际出行时间段与理想出行时间段之差；

M——极大数。

式（8）为轨道交通运营者的目标，min z1表示使旅客出行广义费用最小，max z2表示使轨道交通运营的盈利最大。式（9）为出行者约束，表示j类以l时间段为理想出行时间段的旅客在各时间段出行量要等于该类出行者总和。式（10）为轨道交通运营能力约束，表示某一时间段出行的旅客数量不能高于该时间段轨道交通的运输能力。式（11）为动态广义费用，当旅客理想出行时间与实际出行时间相符时，其广义费用为最低；若出行时间早于或者晚于理想出行时间，广义费用就要增加；当广义费用大于其他交通方式或实际出行时间与理想出行时间之差超过一定值时，其广义费用为无限大，即旅客放弃轨道交通出行。

3.3 算法设计

由于模型目标函数和约束条件都可简化为线性函数，因此本文采用逐步法求解。逐步法是迭代法的一种，在求解过程中，每进行一步，都对其结果进行满意度评价，若符合要求，则停止迭代；否则再根据满意度要求进行修改和再计算，直到达到满意度要求为止。求解计算分为以下3个步骤：

第一步：分别求min z1和max z2的解x1、x2。本模型可转化为运输问题，可采用表上作业法中的伏格尔法进行求解，具体方法见文献［9］。求出x1和x2后，作表Z=（zij），其中zij表示将方案xj代入目标值zi得到的值，可见，当i=j时，zij得到最大值Mj，见表1。

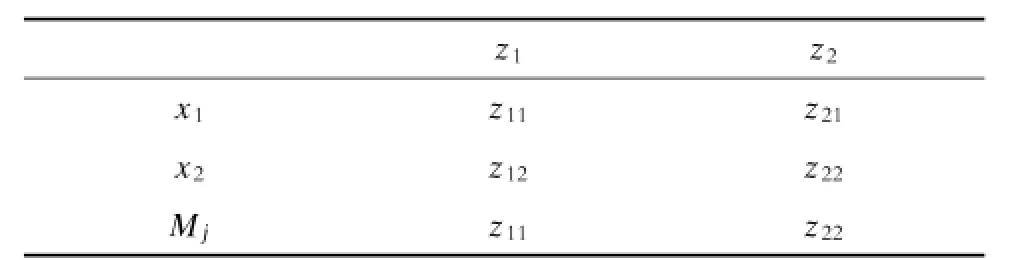
表1 单目标最优解的目标函数值

第二步：求权重系数。设mj=min zij，为了找出目标值的相对偏差以及消除不同目标值的量纲不同的问题，进行如下处理：

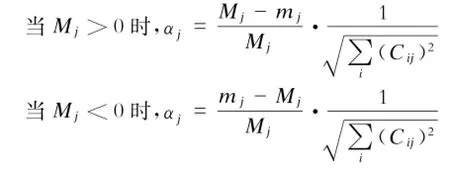
上式中，Cij为目标函数Zj的变量系数，经归一化后，得权重系数：

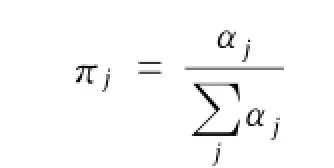
第三步：构造以下线性规划问题，并求解。

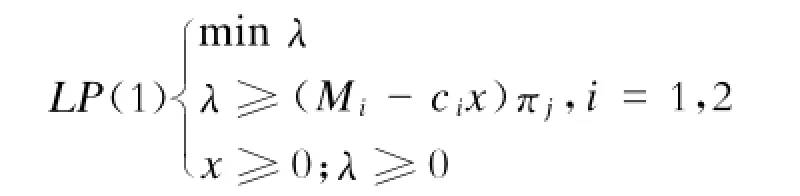
假定求得的解为x—1，相应的两个目标值为C1x—1和C2x—1。若x1为决策者的理想解，其相应的两个目标值为C1x1和C2x2，这时，决策者将x—1的目标值进行比较后认为满意就可以停止计算；若认为相差太远，则考虑适当修正，如考虑对j个目标宽容一下再进行求解。如此重复，直到达到满意值为止。

4 案例分析

本文以与东莞市相接的各种轨道交通模式的客流划分为案例，对模型的应用进行研究。根据相关规划，至2020年，能够为东莞市提供服务的轨道交通线路有：1条高速铁路（广深港客运专线）、2条城际轨道交通（穗莞深城际轨道交通和莞惠城际轨道交通）、2条普通铁路（广深铁路和京九铁路）。根据有关预测，到2020年，轨道交通系统承担的东莞—广州的城际客流将占总客流的35%。

4.1 各种轨道交通模式的广义费用函数

（1）确定理想出行时间下各种轨道交通模式的广义费用权重系数。分别在东莞市的南城区、莞城区、万江区、东城区调查了500、200、200和300名去往广州方向的旅客。将被调查旅客的月收入水平分为4类：3 000元以下、3 001~5 000元、5 001~ 7 000元、7 001元以上。对于每一类，统计出行费用、出行时间和便利性，然后算出其平均值。再按照算法，计算得出权重系数（见表2）。

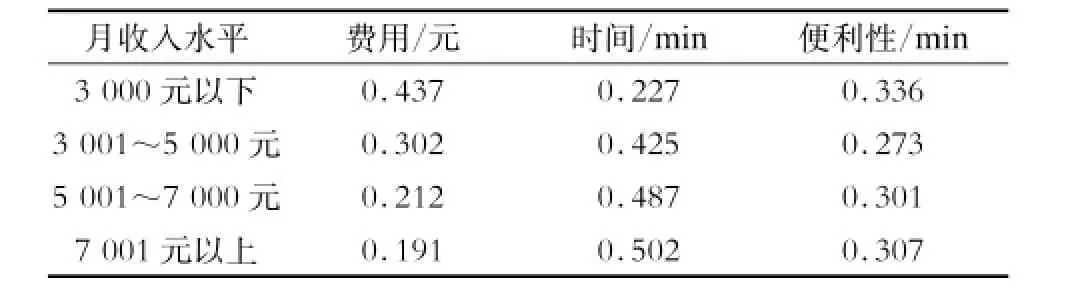
表2 不同月收入水平旅客的指标权重系数

（2）确定理想出行时间下不同轨道交通模式的动态广义费用值。东莞到广州的旅客选择不同轨道模式的费用、时间、便利性数值如表3所示。

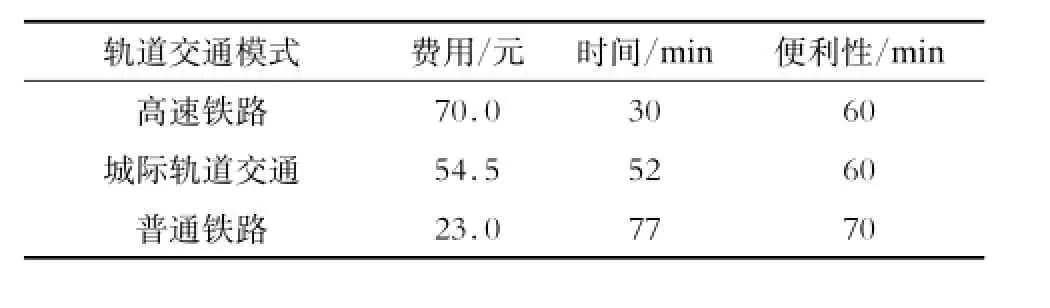
表3 不同轨道交通模式的指标值

把不同月收入水平旅客的指标权重系数，不同轨道交通模式的费用、时间、便利性的值，以及不同收入等级旅客的时间价值代入式（1），得到不同收入等级旅客理想出行时间的广义费用值（见表4）。

（3）确定动态时间广义费用。根据现状客流分布，将一天分为1~9不同的时间段。

出行时间差对应的广义费用为理想出行时间段与实际出行时间段对应的广义费用之差的绝对值。不同月收入水平旅客单位出行时间差对应的广义费用从低到高分别为5元、10元、15元和20元。若出行时间差大于等于3个时间段或者大于其他交通方式的广义费用，则广义费用为无限大，表示为M。由于不同收入阶段使用公路出行广义费用要考虑进城以后城市内的交通状况，因此，为了简化计算，本案例只假设公路出行广义费用大于出行时间差在3个时间段以上的实际轨道交通出行广义费用。

表4 不同收入等级旅客的理想出行时间广义费用值元/人次

4.2 模型求解

结合2009年Stated Preference的调查数据，确定不同收入水平旅客在不同时间段的出行情况如表5。据此，可算出旅客在各实际出行时间段的广义费用。将相关数据代入再划分模型，即可得出不同轨道交通模式所承担的客流量及其分担率和票价收入（见表6）。轨道交通运营部门总票价收入为2 410万元，总广义费用约为1 569万元。从划分结果来看，随着中高收入人群比例的增加，城际轨道交通所占客流分担比例最高，为70.8%，符合未来珠三角地区轨道交通发展趋势。

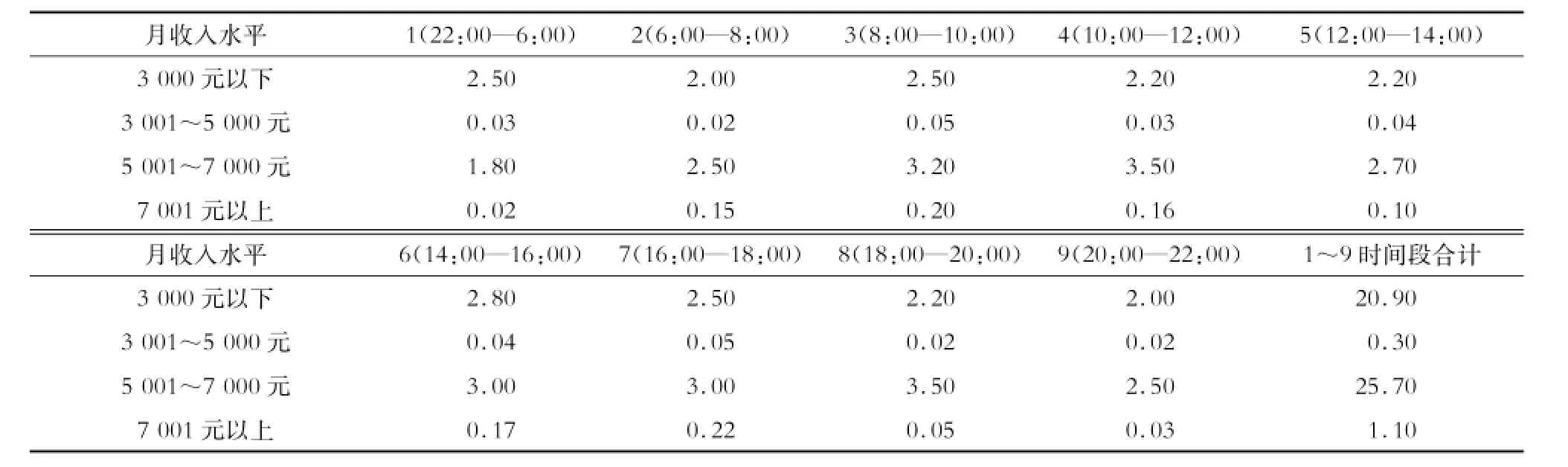
表5 不同收入水平旅客在不同时间段的出行情况万人次

表6 不同轨道交通模式所承担的客流量及其分担率和票价收入

5 结语

在我国经济发达地区多模式轨道交通发展迅速的新形势下，如何正确划分其客流是决策者面临的难题。本文考虑轨道交通运营时间相比运营票价有较大的灵活性，以及轨道交通出行者受时间约束较大的特点而提出的基于动态广义费用的优化模型，贴近实际情况，可为轨道交通运营部门的合理决策作出参考。

［1］ 高杨斌.区域综合交通体系战略规划研究［D］.南京：东南大学，2005：54.

［2］ 郭春江.高速铁路与民航客运量分担博弈模型研究［D］.北京：北京交通大学，2011：7.

［3］ 张力.基于广义费用的客运专线客运需求预测方法研究［D］.北京：北京交通大学，2010：27.

［4］ 邹志红，孙靖南，任广平，等.模糊评价因子的熵权法赋权及其在水质评价中的应用［J］.环境科学学报，2005，25（4）：552.

［5］ 吴峰，施其洲.基于熵值理论的产业结构与交通运输结构关系研究［J］.交通运输工程与信息，2006（1）：71.

［6］ Peterson E R.A highway corridor planning modal：QROAD［J］.Transportation Research Part A，2002，36（2）：107.

［7］ Pitaksringkarn J.The use of micro-simulation modeling in the comprehensive transportation planning process：San Diego’s experience［J］.Journal of the Eastern Asia Society for Transportaion Studies，2003，5：2123.

［8］ Christopher Kennedy.The four pillars of sustainable urban transportation［J］.Transport Review，2005，25（4）：393.

［9］ 钱颂迪，胡云权.运筹学［M］.北京：清华大学出版社，1990.

［10］ 董志国.上海轨道交通出行方式链模型研究［J］.城市轨道交通研究，2012（7）：15.

On Split Model of Railway Transit Passenger Flow Based on Dynamic Generalized Cost

Wu Shimei，Pei Yulong，Cheng Guozhu

According to the big impact of the operation time on railway transit，and based on the dynamic generalized cost caused by the difference between ideal travel time and actural travel time，a double objective optimization model is established，which helps to realize the least generalized cost of different income levels and the highest benefit of railway operation departments.The passenger flow on Dongguan-Guangzhou railway is used as an example to verify the model，and the results are consistent with the railway transit development trend，the feasibility and rationality of the model is proved.

rail transit；passenger flow；dynamic generalized cost；double objective optimization model

2013-10-09）

F 530.5