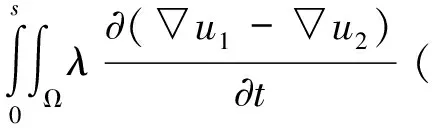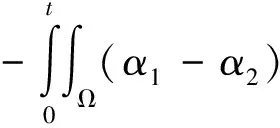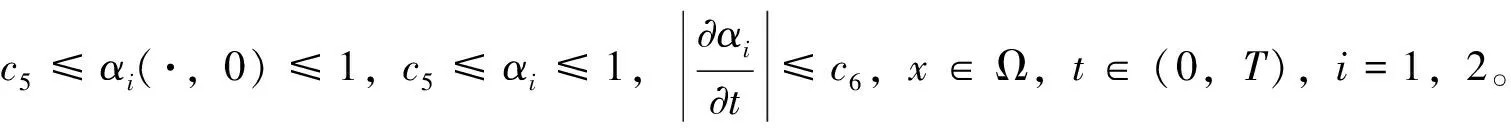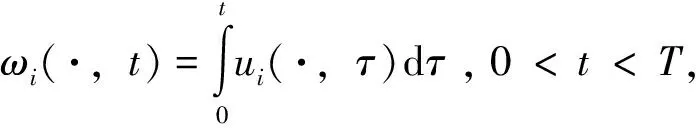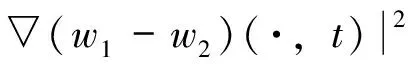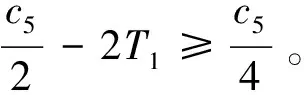一类粘性扩散方程弱解的存在唯一性*
曲程远,魏晓丹
(1.大连民族学院理学院,辽宁 大连 116600;2.大连民族学院计算机科学与工程学院,辽宁 大连 116600)
本文旨在讨论如下粘性扩散方程初边值问题的弱解的存在唯一性,
▽u)=0,
x∈Ω,0 (1) u(x,0)=u0(x),x∈Ω (2) (3) 近年来,众多数学工作者开展了对伪抛物型方程的理论研究。如KAKINA等[7],CAO等[8]建立了具内部源的伪抛物型方程的指标理论;TERRACINA等[9]利用伪抛物正则化,对具cubic-like形式响应函数的正倒向非线性扩散方程弱熵解的存在唯一性做了一系列的讨论。 对形如方程(1)的非线性伪抛物方程的研究始于上世纪70年代,DAVIS于1972年就研究了伪抛物型方程的初边值问题整体解的存在性。 GLADKOV[10]研究了伪抛物型方程的Cauchy问题解的唯一性。 然而对问题(1)-(3)解的存在唯一性,还未见完整讨论。在本文中,我们利用不动点方法给出弱解的存在性,进一步证明了弱解的唯一性。 本文安排如下:第一部分证明问题(1)-(3)弱解的存在性,第二部分给出唯一性。 令空间W={w∈L∞(0,T;H1(Ω));wt∈L∞(0,T;H1(Ω))},W是一个Banach空间,具有范数‖w‖W=‖w‖L∞(0,T;H1(Ω))+‖wt‖L∞(0,T;H1(Ω))。本文中我们考虑的弱解定义如下 定义1 称u为问题(1)-(3)的弱解,如果u∈W, 满足积分等式 ▽φ+ g(|▽Gσ*u|)▽u·▽φ)dx=0, ∀φ∈H1(Ω),t∈(0,T) 并且 为利用Schauder不动点定理来证明弱解的存在性,我们首先讨论如下的线性化问题 ▽u)=0, x∈Ω,t∈(0,T) (4) 其中c(x,t)是一个给定的具有正下界的函数,且∂c/∂t有界。由经典理论[11]可知,问题 (2)-(4)弱解的存在唯一性可以利用Galerkin方法得到。 命题1 对任意的u0∈H1(Ω),线性化问题(2)-(4)具有唯一弱解u∈W。 定理1 若u0∈H1(Ω),问题(1)-(3)存在弱解。 证明这里我们采用Schauder不动点理论来证明。令w∈W,使得 ‖w‖L∞(0,T;L2(Ω))+‖wt‖L∞(0,T;L2(Ω))≤c1‖u0‖H1(Ω) 其中c1为待定正常数。因为w,∂w/∂t满足上式,则有▽Gσ*w和▽Gσ*wt属于L∞(0,T;C∞(Ω)),且存在依赖于Gσ和Ω的常数c2,使得 ‖▽Gσ*w‖L∞(0,T;L∞(Ω))≤c1c2‖u0‖H′(Ω), ‖▽Gσ*wt‖L∞(0,T;L∞(Ω))≤c1c2‖u0‖H′(Ω) 因此有 (5) 考虑如下问题 ▽φ+ g(|▽Gσ*w|)▽u·▽φ)dx=0, ∀φ∈H1(Ω),t∈(0,T) (6) 由式(5)和命题1,问题(6)具有唯一解uw∈W。 令φ=uω,代入问题(6)并从 0到t上积分有 于是可得 (7) ▽uw|2dx. 由式(7)有 (8) ‖▽uw‖L∞(0,T;L2(Ω))≤c3, (9) 我们引入如下定义的子空间W0 W0={w∈W;w在弱意义下满足(2)和(3), c1‖u0‖H1(Ω),‖▽w‖L∞((0,T);L2(Ω))≤c3, 为了利用Schauder不动点定理,我们需要证明P:w→uw从W0到W0弱连续。令wj为W0中一列弱收敛于w的序列,uj=uwj。往证P(wj)=uj弱收敛于P(w)=uw。根据式(7)-(9)和Sobolev空间中的经典结论,我们可以从uj得到一个收敛于u的子列,使得 wj→w在L2(0,T;L2(Ω))中且几乎处处于Ω×(0,T)上; g(|▽Gσ*wj|)→g(|▽Gσ*w|) 在L2(0,T;L2(Ω))中且几乎处处于Ω×(0,T)上; uj→u在L∞(0,T;L2(Ω))中弱收敛; uj→u在L2(0,T;L2(Ω))中和且几乎处处于Ω×(0,T)上; uj(x,0)→u0(x) 在L2(Ω)中; 通过以上收敛我们得到u=P(w)。由于问题(6)的解是唯一的,序列uj=P(wj)在W0中弱收敛于u=P(w),即P弱连续。根据Schauder不动点定理,存在w∈W0使得w=P(w)=uw,即uw为问题(1)-(3)的解。 定理2 问题(1)-(3)的弱解是唯一的。 证明令u1,u2为(1)-(3)两个弱解。则对于几乎每一个(0,T)中的t和i=1,2,我们有 div(α1▽(u1-u2))=div((α1-α2)▽u2), x∈Ω,0 (10) u1(x,0)-u2(x,0)=0,x∈Ω (11) (12) 其中αi(x,t)=g(|▽Gσ*ui|)。 令0 α1▽(u1-u2)▽(v1-v2))dxdt+ (13) (14) 由于g(s)和Gσ是光滑的,我们有‖α1-α2‖L∞(Ω)≤c7‖u1-u2‖L2(Ω),其中c7是取决于g(s)和Gσ的常数。对式(14)使用Young不等式,得到 (15) 2cs‖▽(w1-w2)(·,s)‖L2(Ω) 则由Gronwall不等式的积分形式可知在(0,T1]上u1-u2≡0。最后,在区间(T1,2T1],(2T1,3T1]等上进行同样的步骤,最终在(0,T)上得到u1≡u2。 参考文献: [1]VAN DUJIN C J, FAN Y, PELETIER L A, et al. Travelling wave solutions for degenerate pseudo-parabolic equation modelling two-phase flow in porous media [J]. Nonlinear Anal Real World Appl, 2013, 14(3): 1361-1383. [2]CUESTA C M. Linear stability analysis of travelling waves for a pseudo-parabolic Burgers’ equation [J]. Dynamics of PDE, 2010, 7(1): 77-105. [4]PERNA P, MALIK J. Scale-space and edge detection using anisotropic diffusion [J]. IEEE Trans on Pattern Anal Machine Intell, 1990,12(7): 629-639. [6]ELLIOTT C M, GAWRON B, MAIER-PAAPE S, et al. Discrete dynamics for convex and non-convex smoothing functionals in PDE based image restoration [J]. Commun Pure Appl Anal, 2006, 5(1): 181-200. [8]CAO Y, YIN J X, WANG C P. Cauchy problems of semilinear pseudo-parabolic equations [J]. J. Differential Equations, 2009, 246: 4568-4590. [9]TERRACINA A. Qualitative behavior of the two-phase entropy solution of a forward-backward parabolic problem [J]. SIAM J Math Anal, 2011, 43: 228-252. [10]GLADKOV A L. Uniqueness solvability of the Cauchy problem for certain quasilinear pseudoparabolic equations [J]. Mathematical Notes, 1996, 60(3): 264-268. [11]EVANS L C. Partial differential equations [M]. 2nd ed, Rhode Island: American Mathematical Socitety, 2010.

1 弱解的存在性


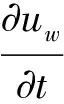

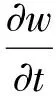

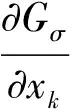
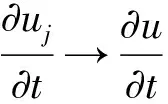


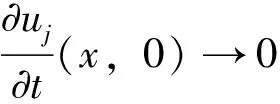
2 弱解的唯一性