双输入样条神经网络权值与结构确定算法*
杨文光,钟云香,李强丽,张 军
(1.华北科技学院基础部,河北 三河 065201;2. 华北科技学院科技管理处,河北 三河 065201)
目前,前馈型神经网络是应用最为广泛,研究最为成熟的一种人工神经网络模型,该类型神经网络包括感知器、BP神经网络、径向基函数(RBF)神经网络等。由于这种神经网络具有较好的收敛速度、构造相对简单,且能够较好的逼近未知目标函数,而在模式识别、系统辨识、信号处理和控制等学科领域有大量的应用[1-3]。随着处理问题复杂程度的加大和非线性因素的增多,解决多输入单输出系统的高精度建模问题日渐成为研究的热点,文[4-6]对传统BP神经网络进行了改进,推导得到了权值直接确定算法,该算法极大简化了网络的设计和运行时间。文[7]充分考虑训练数据的重要程度的不同,将模糊数学中隶属函数与激励函数进行了有机结合,在权值直接确定法基础上,解决了双输入单输出系统的简单化结构确定问题。此外,文[8-11]从理论上对前馈型神经网络进行了探讨,丰富了网络的构造方法。
本文依据函数逼近理论,将乘积型样条函数引入到双输入样条神经网络的构建中,在网络建立过程中,紧密结合输入变量的网络结构,实现由单输入到双输入结构的过渡,得到三层前馈型神经网络,解决大数量训练数据下的权值矩阵的直接确定问题。该网络充分考虑到了输入数据的空间结构,可以设计算法升级到多输入系统的建模中去,最后结合仿真实验,进一步说明算法的有效性。
1 双输入样条神经网络结构
文[12]利用样条函数巧妙构造了隐层神经元激励函数,设计出了权值直接确定的样条神经网络,解决了单输入单输出系统的建模与预测问题,但该模型却没有解决多输入多输出系统的建模与预测问题。在笔者前期研究工作基础上[7],下面设计一种双输入单输出的样条前向神经网络,该模型含有输入层、隐层、输出层三层,见图1。
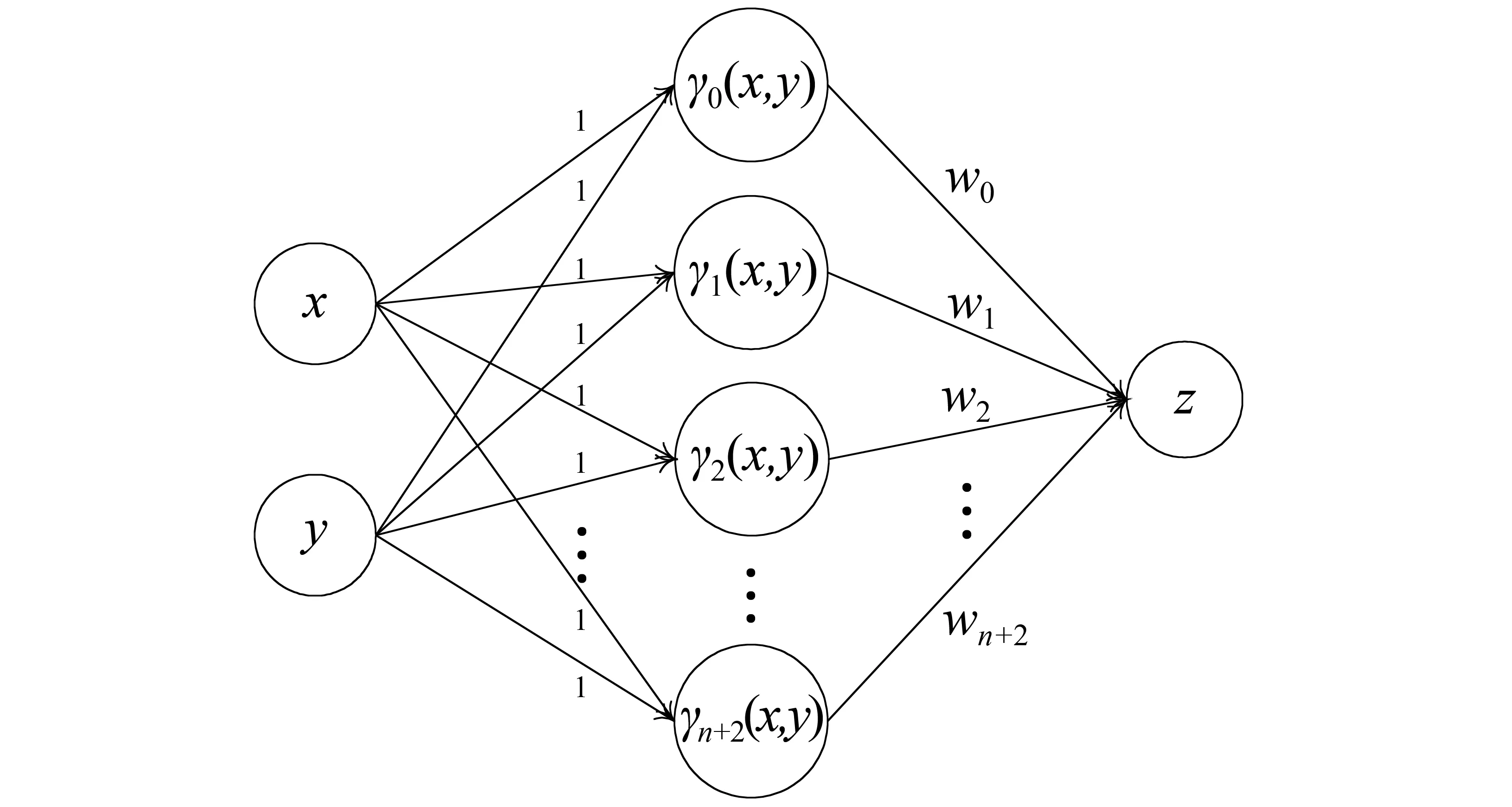
图1 双输入三层前馈神经网络
类似于RBF神经网络,设定输入层神经元到隐层神经元连接权值全部为1,隐层神经元到输出层神经元连接权值向量为w= (w0,w1,…,wn+2)T∈Rn+3,输出层为隐层输出的线性加权求和,则与图1吻合的三层样条前向神经网络模型为
(1)
其中γi(x,y)为隐层第i个神经元的激励函数输出,不同于传统BP神经网络隐层神经元选择为Sigomoid函数,设γ=(γ0(x,y),γ1(x,y),…,γn+2(x,y))∈R1×(n+3),在式(1)中γi(x,y)选择为样条函数的适当组合,i=0,1,…,n+2。
定义1[13]设α(x)是定义在区间[a,b]上的函数,在[a,b]上有一个划分△x:
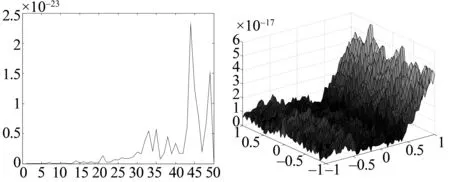
a=x0 α(x)满足如下条件: (i)α(x)在每个子区间△xi=[xi-1,xi](i=1,2,…,n)上都是不超过3次的多项式,至少在一个子区间上为3次的多项式; (ii)α(x)是2次连续,即α(x)∈C2[a,b],则称α(x)是关于划分△x的一个3次样条函数。 同样假定在下面讨论的β(y)是定义在区间[c,d]上关于划分△y上的一个3次样条函数,其中△y: c=y0 注1 下面选择的[c,d]分划数与[a,b]分划数不同,当然亦可以相同,二者的分划是任意的,可以是等距划分也可以是非等距划分。 i=1,2,…,n-1 i=1,2,…,n-1 (2) 这种改写使得原点成为间断点,但却带来了线性无关,作为一组函数系用于构造激励函数却带来便利。 i=1,2,…,n-1 (3) 设区间[a,b]划分数为n+1,[c,d]分划数为n+3且数据无缺失的情况下,输入平面[a,b]×[c,d]上面就存在(n+1)×(n+3)个输入数据点,三维空间也就存在(n+1)×(n+3)个点,具体取值见表1。 表1 双输入单输出系统采样数据 对输入数据进行网格化后,可以先固定x,对y依次设计三次样条神经网络,或者先固定y,对x依次设计三次样条神经网络,然后再将网络推广到二元即得二元双三次样条神经网络,具体操作如下: 比如先固定x,若x=xi,y∈[c,d],可以自由取值,对一些符号进行简记,令γxi=(γ0(xi,y),γ1(xi,y),…,γn+2(xi,y))∈R1×(n+3),wyj= (w0j,w1j,…,wn+2,j)T∈Rn+3,当y=yj或者(x,y)∈δ(xi,yj)时,式⑴不难改写为 (4) 其中δ(xi,yj)表示以点(xi,yj)为中心的半径为δ的邻域,而δ又是到点(x,y)的最小距离,i=0,1,…,n,j=0,1,…,n+2。本文设计的双三次样条神经网络就是在式(4)基础上,完成所有网格化后采样数据的输入,下面将依据权值直接确定法和函数逼近理论,使得网络输出较好的逼近真实系统输出,满足如下条件 ∀ε>0,使得‖zij-f(xi,yj)‖<ε 表1所给出的网格化的采样数据确定了系统内部的函数关系,如何有效利用采样数据还原系统真实信息成为研究多输入复杂系统的热门问题。鉴于前向神经网络确立原则,需要使用训练数据对网络进行训练,使其达到预期的逼近精度。考虑到系统的建立需要大量的训练数据,现将已经网格化的表1所列数据作为训练数据,在表1的网格外侧随机抽取若干真实数据作为验证数据。下面建立依据双输入样条神经网络的权值直接确定算法,并设计满足误差要求的网络结构确定算法。 为了更好地说明双输入样条神经网络的权值直接确定算法,下面给出相关的定义和理论依据。 定义2[16]设实矩阵X∈Rn×m,如果U∈Rm×n,满足XUX=X,UXU=U,(XU)T=XU,(UX)T=UX,则称U为X的Moore-Penrose广义逆矩阵或伪逆,记作X+。 定义4[11,17]设G⊂C(Ω)是一个代数,φ(P)∈C(Ω),若∀ε>0,且∀P1,P2∈Ω,均可以找到一个逼近函数f(x,y)∈Ω,使得 |φ(Pi)-f(Pi)|<ε,i=1,2 那么称目标函数φ可用G中元素一致逼近,其中|·|表示标量的绝对值。 引理2[11,17]设x,y∈R,φ(x,y)是定义在Ω⊂R2上的连续目标函数,则φ(x,y)在Ω⊂R2上可用关于x,y的多项式f(x,y)∈Ω进行逼近。 文[12]在前向神经网络基础上变换隐层神经元激励函数,利用伪逆得到了相应网络结构的最优权值,对于单输入单输出未知系统,存在文[12]设计的单输入单输出样条神经网络可以实现未知系统的最小二乘逼近,同样对于双输入单输出未知系统,亦可以设计出式(4)对应下的网格化下的双输入单输出样条神经网络,随着某个变量如x的变化下最终实现二元双输入样条神经网络的逼近,由误差反向传播学习算法亦可得如下权值直接确定定理。 定理3 按照式(4)建立的双输入样条神经网络在输入训练数据集为A= ((x0,y0,z00),(x0,y1,z01),…,(xn,yn+2,zn,n+2))时,设wopt∈R(n+3)×(n+1)是隐层与输出层神经元之间的最优连接权值矩阵,输入受激励矩阵X∈R(n+1)×(n+3),目标输出矩阵Z∈R(n+1)×(n+3),则双输入样条神经网络的最优权值矩阵为 wopt=(XTX)-1XTZ=X+Z (5) 其中 ∈R(n+1)×(n+3) 证明定义训练数据总误差为 (6) 首先总误差对权值矩阵求偏导,不难计算得到 XT(Xw(k)-Z) 利用误差反向传播学习BP算法,计算最优权值矩阵wopt,权值矩阵的迭代公式为 w(k+1)=w(k)-ηXT(Xw(k)-Z) (7) 对式(7)两边求极限得最优权值矩阵wopt=(XTX)-1XTZ=X+Z,学习率η取为1。 双输入样条神经网络的实现较之单输入样条神经网络要复杂,需要对改写后的截断幂函数和权值直接确定最优权值矩阵有清楚的认识。为了满足建模精度要求,设置总误差要求为ε,假设在下面的实验中对变量x,y所在的取值区间[a,b]与[c,d]进行等距划分,[a,b]划分数为n,[c,d] 划分数为n+2,设隐层神经元个数为n+3,训练数据总数为(n+1)×(n+3),这里的n可以按照ε的设置进行增加或减少,以满足误差要求,具体实现步骤如下。 步骤1 根据区间[a,b]与[c,d]的划分数,对输入变量进行网格化划分,生成输出矩阵Z,提取训练数据得到真实模型; 步骤2 计算输入受激励矩阵X,调用MATLAB中的pinv(X)得到伪逆X+,按照公式⑸计算与步骤1对应划分下的最优权值矩阵wopt; 步骤3 由公式⑹计算总误差e,若e≤ε,则记录下划分数n,否则令n+1→n,跳至步骤1; 步骤4 若在获得尽可能多的训练数据情况下保证建模精度,则继续增大n,执行步骤1、2,直到最大的循环次数c,记录每次的总误差e,在保证建模精度的情况下,即满足ε要求下寻找最大的划分数nmax; 步骤5 确定隐层神经元个数,亦即确定网络结构,若验证数据落在区域[a,b]×[c,d]内,可以直接对验证数据所在邻域的顶点输出求均值来确定输出,预测误差较小;若验证数据落在区域[a,b]×[c,d]外,则需采用公式⑷进行网络近似预测,误差相对大些。 下面选择文[4]中出现的二元函数作为真实模型,给出逼近模型,并比较一些统计参数,如算法运行时间、总误差、隐层神经元个数等。本文实验的硬件电脑为方正台式机配置是Pentium(R) Dual-Core CPU E5200 @ 2.5GHZ,内存为2.00G,32位操作系统。输入变量x∈[-1,1],y∈[-1,1],给定初始区间划分数n=5,总误差初始要求ε=10-23,设定的循环次数为c=50次,利用MATLAB7.5.0(R2007b)对目标函数1、2进行了建模。对于目标函数2,由于在取值区间内,可出现分母为0的情况,故给其分母加上一个非常小的数,以避免出现无法建模的问题。 目标函数1:z=ysin(x+y)exp(-y2)+1 图4 目标函数2与逼近模型 图5 逼近模型总误差趋势与平均误差 较之文[4],本文提出的双输入样条神经网络在较短时间内取得了更好的仿真效果,建模的总误差都在10-24以上的数量级,逼近精度进一步提高,网络输出数据与训练数据基本完全重合,运行时间仅仅约0.2s~0.3s左右,具体参数指标见表2。表2给出了目标函数1、2网络的训练时间,满足精度要求的区间划分数nmax及其对应的总误差e,另外随机给出了目标函数1、2在区域[-1,1]×[-1,1]内一组验证数据(-0.984,0.975)的验证数据相对误差。 表2 网络性能 对于多输入单输出系统,采样数据往往是以空间形式存在的,基于此本文提出了三层双输入单输出的样条神经网络建模方法。该网络不同于现有多输入网络忽视数据空间结构的现状,实现了输入变量的网格化划分,网络结构可以随训练数据和网格划分数的变化而进行调整,网络权值随数据空间位置的改变而变化,生成的权值矩阵做到了一步直接确定。最后的仿真实验表明,双输入样条神经网络具有较高的建模精度,这为后续研究多输入神经网络解决复杂数据系统的实时性高精度建模与预测问题提供了可借鉴的思路。 参考文献: [1]周辉仁,郑丕谔. 四层BP神经网络的一种结构设计方法及应用[J]. 系统仿真学报, 2008, 21(9): 2325-2333. [2]周春光,张冰,梁艳春,等. 模糊神经网络及其在时间序列分析中的应用[J]. 软件学报, 1999,10(12):1304-1309. [3]沈谦,王涛,张德龙. 基于模糊前向神经网络的PVC识别方法[J]. 计算机工程与科学, 2000, 22(6): 60-62. [4]张雨浓,劳稳超,余晓填,等. 两输入幂激励前向神经网络权值与结构确定[J]. 计算机工程与应用, 2012, 48(15): 102-106. [5]张雨浓,曲璐,陈俊维,等. 多输入Sigmoid激励函数神经网络权值与结构确定法[J]. 计算机应用研究, 2012, 29(11):4113-4151. [6]肖秀春,张雨浓,姜孝华. MISO多元广义多项式神经网络及其权值直接求解[J]. 中山大学学报:自然科学版, 2009,48(4):42-56. [7]杨文光,闫守峰,文小艳. 双输入型模糊前向神经网络的构建[J]. 湖南师范大学:自然科学学报, 2013, 36(3): 33-38. [8]王建军,徐宗本. 多元多项式函数的三层前向神经网络逼近方法[J]. 计算机学报, 2009, 32(12): 2482-2488. [9]曹飞龙,张永全,潘星. 构造前向神经网络逼近多项式函数[J]. 模式识别与人工智能, 2007, 20(3): 331-335. [10]曹飞龙,徐宗本. 多变元周期函数的神经网络逼近:逼近阶估计[J]. 计算机学报, 2001, 24(9): 903-908. [11]ZHANG Y N, WANG J. Recurrent neural networks for nonlinear output regulation [J]. Automatica, 2001, 37(8): 1161-1173. [12]张雨浓,杨逸文,肖秀春,等. 样条神经网络的权值直接确定法[J]. 系统工程与电子技术, 2009, 31(11): 2685-2688. [13]吴勃英,王德明. 数值分析原理[M]. 北京:科学出版社, 2007. [14]朱长青. 双三次样条插值函数乘积型计算原理及其应用[J]. 测绘工程, 1998, 7(2):17-21. [15]朱长青. 数值计算方法及其应用[M]. 北京:科学出版社, 2006. [16]史荣昌,魏丰. 矩阵分析[M]. 北京:北京理工大学出版社, 2010. [17]梁学章,李强. 多元逼近理论[M]. 北京:国防工业出版社, 2005.




2 双输入样条神经网络权值与结构确定算法
2.1 权值直接确定
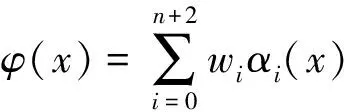
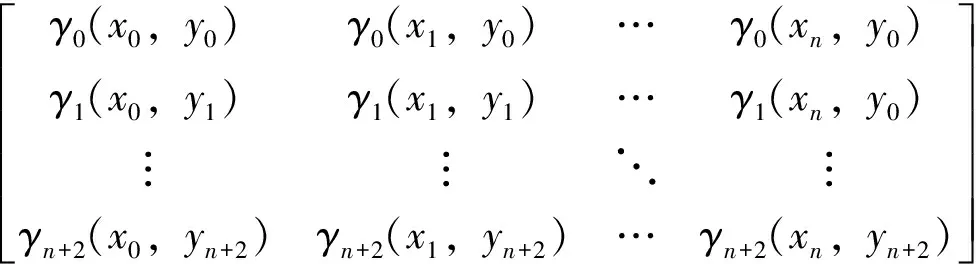
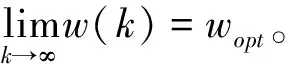
2.2 权值直接确定算法和网络结构实现
3 仿真实验
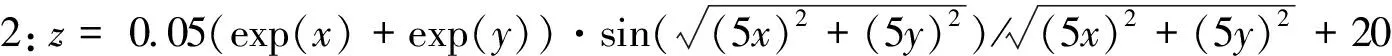


4 结束语

