具阻尼项的高阶中立型泛函微分方程的振荡性*
杨甲山
(梧州学院数理系, 广西 梧州 543002)
考虑如下一类高阶非线性变时滞阻尼泛函微分方程
Q(t)f(φ(x(δ(t))))=0,t≥t0
(1)
其中n≥2为偶数,t0≥0为常数,z(t)=x(t)+P(t)x(τ(t)),A(t),P(t),Q(t)∈C([t0,+∞),R),φ(u)=|u|γ-1u,γ>0为常数;f(u)∈C(R,R)且uf(u)>0(u≠0)。本文总假设下列条件成立:
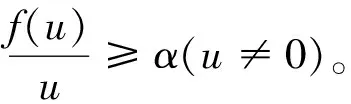
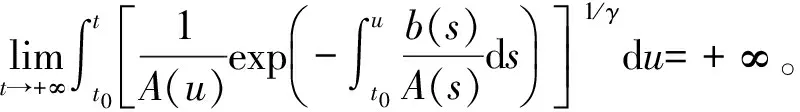
关于方程(1)的特殊情形及其振荡性结果见文[1-4]。若方程(1)中P(t)≡0,f(u)=u,则可简化为
[A(t)φ(x(n-1)(t))]′+b(t)φ(x(n-1)(t))+
Q(t)φ(x(δ(t)))=0
(2)
而方程(2)的振荡性在文[5]也作了仔细研究,并给出了3个非常有价值的振荡准则。本文的目的是研究方程(1)振荡性,并给出当文[5]中定理3的条件(C9)(文[6-16]也有类似的条件)不成立时的一些新的振荡准则。
1 几个引理
引理1[6]设u在[t0,+∞)上是正的n次可微函数,u(n)(t)最终定号,则存在t*≥t0和整数l(0≤l≤n),当u(n)(t)≥0时,n+l为偶数;当u(n)(t)≤0时,n+l为奇数,使得
当l>0时,有u(k)(t)>0,t≥t*,k=0,1,…,l-1;
且当l≤n-1时,有(-1)l+ku(k)(t)>0,t≥t*,k=l,l+1,…,n-1
引理2[7]设u满足引理1的条件,且u(n-1)(t)u(n)(t)≤0(t≥t*),则对任何θ∈(0,1),存在常数M>0, 使得对一切充分大的t有u′(θt)≥Mtn-2u(n-1)(t)。
引理3[8]设a,b为非负实数,则λabλ-1-aλ≤(λ-1)bλ,λ>1,等号成立当且仅当a=b。
引理4 设x(t)是方程(1)的最终正解,则z(t)>0,z′(t)>0,z(n-1)(t)>0,z(n)(t)≤0。
证明完全类似于文[5]中的引理4,在此从略。
2 主要结果和证明
为了叙述方便,考虑集合D={(t,s)|t≥s≥t0},D0={(t,s)|t>s≥t0}。称函数H∈Y,如果函数H(t,s)∈C(D,R),当t≥t0时H(t,t)=0; 当(t,s)∈D0时H(t,s)>0且H(t,s)对第二个变量有连续非正的偏导数。
引入记号
Φ(s)=αQ(s)[1-P(δ(s))]γ,
(3)
定理1 若存在函数H∈Y及ζ(t)∈C1([t0,+∞),(0,+∞)),使得
(4)
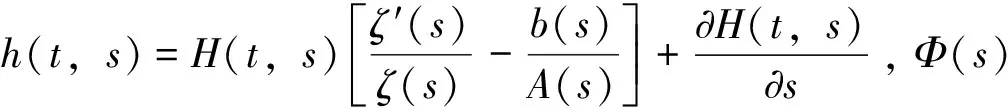
证明设方程(1)存在非振荡解x(t)。不失一般性,设x(t)>0,x(τ(t))>0,x(δ(t))>0,t≥T≥t0。由方程(1)并注意到条件(H3),得
[A(t)φ(z(n-1)(t))]′+b(t)φ(z(n-1)(t))≤
-αQ(t)φ(x(δ(t)))<0
(5)
由引理2,对0<θ<1,存在常数M>0,有
z′(θδ(t))≥Mδn-2(t)z(n-1)(δ(t))≥
Mδn-2(t)z(n-1)(t)
(6)
由x(t)≤z(t)及引理4知,z(t)≤x(t)+P(t)z(τ(t))≤x(t)+P(t)z(t),即
x(t)≥[1-P(t)]z(t)≥0
(7)
定义函数
(8)
则V(t)>0(t≥T),注意到式(5)-(7),可以得到
注意到式(3)的第一个式子,于是由上式,当t≥T时,有
上式两边同乘H(t,s),并从T到t(t≥T)积分,可得




(9)
现取
代入引理3中的不等式,得
|h(t,s)|V(s)-
(10)
将式(10)代入式(9),有

(11)
即
H(t,t0)V(T)
(12)
于是



注1 通过选择恰当的不同的函数H(t,s)和ζ(s)就能导出许多关于方程(1)及其特殊情形的不同类型的其它具体振荡准则。如,若方程(1)中n=2,P(t)≡0,f(u)=u,δ(t)=t,并在定理1中取ζ(s)=1,于是由定理1,我们可得如下结果。
推论1 若存在函数H∈Y, 使得
[H(t,s)Q(s)-

[A(t)|x′(t)|γ-1x′(t)]′+b(t)|x′(t)|γ-1·
x′(t)+Q(t)|x(t)|γ-1x(t)=0
是振荡的。
这是Li等[9]将Philos型振荡准则推广到了二阶半线性阻尼微分方程所得到的结果。本文将其推广到了具有阻尼项的高阶非线性中立型变时滞微分方程(1)。又如取H(t,s)=(t-s)k,由定理1,可得如下结果。
推论2 如果存在常数k>γ及函数ζ(t)∈C1([t0,+∞),(0,+∞)),使得
其中常数θ∈(0,1)和M>0如引理2,函数Φ(s),Ψ(s)定义如式(3)。则方程(1)是振荡的。
若方程(1)中n=2,P(t)≡0,b(t)≡0,f(u)=u,δ(t)=t,并在推论2中取ζ(t)=1,则有
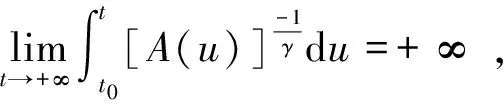
则方程[A(t)φ(x′(t))]′+Q(t)φ(x(t))=0(t≥t0)是振荡的。
推论3就是文[8]中的定理4.7.5,也是Li等[2]推广了Kamenev的结果所得到的结论。
若方程(1)中P(t)≡0,f(u)=u,则定理1即为文[5]中的定理3。其它相关结果可参见文献[10-14]及其参考文献。若式(4)不成立,我们有下面的判别准则。
定理2 若存在函数H∈Y及ζ(t)∈C1([t0,+∞),(0,+∞)),ξ1(t),ξ2(t)∈L2([t0,+∞),R)使得对任意的s≥T,有
(13)
(14)
并且ξ1和ξ2满足
+∞
(15)
其中T≥t0为某常数,常数θ∈(0,1)和M>0如引理2,[ξ1(τ)-ξ2(τ)]+=max{[ξ1(τ)-ξ2(τ)],0},函数Φ(s),ψ(s)及h(t,s)定义如定理1,则方程(1)是振荡的。
证明设方程(1)存在非振荡解x(t)。不失一般性,设x(t)>0,x(τ(t))>0,x(δ(t))>0,t≥T≥t0。 定义函数V(t)如式(8),则由定理1的证明可得式(9)和式(11)。由式(11),当t≥s≥T≥t0时,有

(16)
由式(16),进一步可得
注意到式(13)、式(14),由上式即得
ξ1(s)-ξ2(s)≤V(s),s≥T≥t0
(17)
另一方面,由式(9),有
|h(t,τ)|V(τ)}dτ≤
上式蕴含着
|h(t,τ)|V(τ)}dτ≤V(T)-ξ1(T)≤C0
(18)
式中C0为某常数,并能断言
(19)
于是由式(18),知
(20)
所以,对充分大的正整数n,
于是,对充分大的正整数n及ε∈(0,1),有
1-ε>0
(21)

由上式并注意到式(21),得
由式(14)知,上式右边是有界的,这与式(20)矛盾!所以式(19)是成立的。
由式(19),并注意到式(17),我们有
这与式(15)矛盾! 定理证毕。
适当选取函数H(t,s)和ζ(t),就可以从定理2得到方程(1)的一系列具体振荡准则。例如,取H(t,s)=(t-s)k,ζ(t)≡1,就有
推论4 如果存在函数ξ1(t),ξ2(t)∈L2([t0,+∞),R)及常数k>γ使得
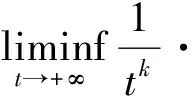
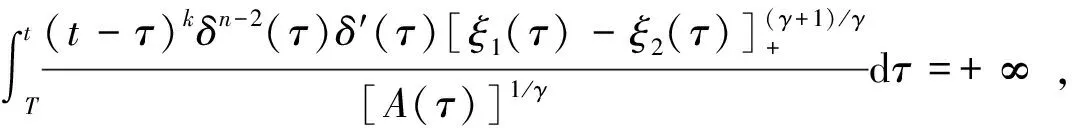
注2 若方程(1)中P(t)≡0,f(u)=u,则本文定理2及推论4得到了文[5]中定理3的条件(C9)不成立时方程(2)的振荡准则。
3 例子
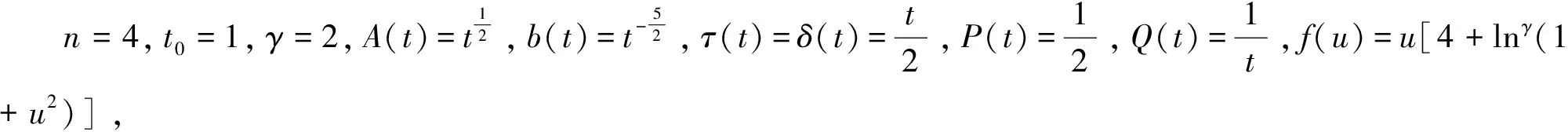
显然条件(H1)-(H5)是满足的。现取ζ(t)=1,H(t,s)=(t-s)3,则此时定理1即为推论2,故有
因此推论2的条件全部满足,于是由推论2知此时方程是振荡的。
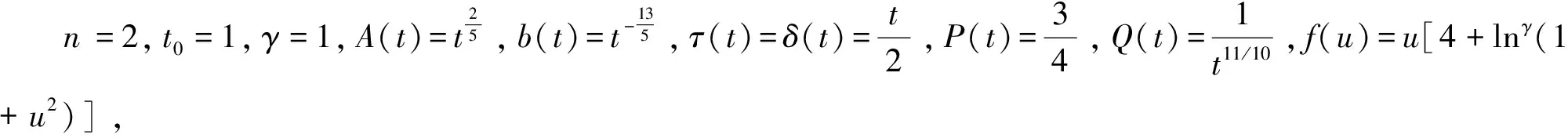
即此时式(4)是不成立的,也就是说文[5]中定理3的条件(C9)不满足,因此,文[5]中定理1-定理3和本文定理1及其推论均不能用。现改用本文定理2(此时定理2即为推论4),则
所以
→+∞(t→+∞)
显然,定理2(推论4)的条件是满足的。于是,由定理2(推论4)知,此时方程是振荡的。但文[5-14]中的定理均不能判定例1和例2中方程的振荡性。
参考文献:
[1]KAMENEV I V. An integral criterion for oscillation of linear differential equations of second order [J]. Math Zametki, 1978, 23: 249-251.
[2]LI H J, YEH C C. An integral criterion for oscillation of nonlinear differential equations [J]. Math Japonica, 1995, 41: 185-188.
[3]PHILOS CH G. Oscillation theorems for linear differential equations of second order [J]. Arch Math, 1989, 53: 482-492.
[4]WANG Q R. Oscillation and asymptotics for second-order half-linear differential equations [J]. Appl Math Comput, 2001, 122: 253-266.
[5]张全信,俞元洪. 偶阶半线性阻尼泛函微分方程的振动性[J]. 应用数学学报, 2010, 33(4): 601-610.
[6]AGARWAL R P, GRACE S R, REGAN D O. Oscillation theory for difference and functional differential equations [M]. New York: Kluwer Academic Publishers, 2000.
[7]GYOR I, LADAS G. Oscillation theory for delay differential equations with applications [M]. Clarendon: Oxford, 1991.
[8]AGARWAL R P, BOHNER M, LI W T. Nonoscillation and oscillation: Theory for functional differential equations [M]. New York: Marcel Dekker, 2004.
[9]LI W T, ZHONG C K, FAN X L. Oscillation criteria for second-order half-linear ordinary differential equations with damping [J]. Rocky Mountain J Math, 2003, 33(1): 1-26.
[10]YANG X J.Oscillation criteria for nonlinear differential equations with damping [J]. Appl Math Comput, 2003, 136: 549-557.
[11]WANG Q R .Oscillation criteria for even order nonlinear damped differential equations [J]. Acta Math Hungar, 2002, 95: 169-178.
[12]WU H W, WANG Q R, XU Y T. Oscillation criteria for certain even order nonlinear functional differential equations [J]. Dynamic Systems and Applications, 2004, 13: 129-144.
[13]杨甲山,方彬. 一类二阶中立型微分方程的振动和非振动准则[J]. 四川师范大学学报:自然科学版,2012,35(6):776-780.
[14]罗李平,俞元洪. 三阶半线性中立型微分方程的振动结果[J]. 系统科学与数学, 2012, 32(5): 571-579.
[15]杨甲山. 具正负系数和阻尼项的高阶微分方程的振动定理[J]. 中山大学学报:自然科学版, 2012, 51(1): 30-34.
[16]林全文,庄容坤. 二阶非线性椭圆型微分方程新的振动准则[J]. 中山大学学报:自然科学版, 2013, 52(2): 57-61.

