基于Copula函数和SPEI的广东北江流域干旱频率分析*

刘占明，陈子燊，黄 强，刘曾美

(1.中山大学水资源与环境系，广东 广州510275；2.华南理工大学水利水电系，广东 广州510640)

干旱是世界上最常见的自然灾害，被认为是全球最严重的自然灾害之一[1]。在我国，干旱被列为气象灾害之首[2]。虽然广东位于华南沿海，降水较多，但在季风、地质条件等多种因素的综合影响下，也饱受干旱困扰。根据统计[3]，广东省约24％的耕地经常遭遇干旱，严重的年份耕地受旱面积超过100万hm2(约占耕地总面积的50％)。

北江起源于南岭山系，是珠江水系第二大支流，流域面积约4.7万 km2，其中广东境内约4.3万km2。由于干旱事件具有多种属性，如Mishra和Singh[4]采用历时、烈度、严重程度等描述干旱，并且这些特征属性间具有一定关联，适宜进行多变量分析。从过去的研究来看，涉及该区域干旱的研究已有较多文献[5-7]，但这些研究多是基于某一评估指标(主要是标准化降水指数SPI)研究干旱某一变量的时空变化特征，较少涉及多变量的概率分析。有研究[8]指出SPI没有考虑温度变化造成的水分支出，对干旱的评估结果还需进一步检验。北江流域属中亚热带向南亚热带过渡区域，温度变化造成的水分支出对于干旱的影响是不容忽视的。近年来，已有学者提出气温对于干旱的重要性并对蒸散发进行了研究与估算[9]。Vicente-Serrano等[10]提出了标准化降水蒸散指数SPEI(the standardized precipitation evapotranspiration index，简称SPEI)。SPEI综合了帕默尔指数(PDSI)对蒸散的响应及SPI多时间尺度的优点，基于概率计算，具有空间可比性的优点，目前已成为研究干旱新的理想指标[11-12]。刘占明等[13]应用7种干旱指标对广东北江流域进行评估，并结合历史干旱资料对比分析，发现SPEI指标的评估结果最能反映该区域的实际情况。众所周知，在气象水文学领域，极端事件的各属性之间普遍存在着相关性，而近10年来在气象水文学领域引入的Copula函数可以描述这种相关性，并且为多变量联合概率分布的研究提供了理论基础和技术手段[14]。

本文选取广东北江流域分布较均匀、数据序列较长且没有发生站点变更的18个国家基本气象站(图1)近50a日均温、日降水数据，数据序列大多起始于1957-1962年，均终止于2007年，数据资料来自国家气象局气象信息中心，均经过了严格的质量控制及三性检查，具有良好的完整性。根据计算出的SPEI值，通过游程理论[15]确定干旱变量，基于概率函数对区域干旱单变量概率分布和两变量联合分布及其带来的干旱风险进行研究，以期为分析区域水量平衡及防灾减害的风险管理提供科学依据。

图1 广东北江流域范围及站点位置

1 研究方法

1.1 标准化蒸散指数(SPEI)

基于水量平衡原理提出的SPEI，首先利用Thornthwaite[16]方法计算潜在月蒸散量，进而以潜在蒸散量与降水量差值的概率分布来表征一个区域净降水量偏离正常的程度。计算方法如下：

1)计算地表月潜在蒸散量

EP=16K(10T/I)a

(1)

式中，Ep为潜在蒸散发量(mm)；T为月平均气温(℃)；I为年热指数，等于一年中各月指数i=(T/5)1.514的累加值；a为经验指数，由与I的函数关系导出：a=6.75×10-7I3-7.71×10-5I2+1.79×10-2I+0.49；修正系数K=(N/12)(M/30)，其中，M为每月的天数，N为最大日照时数，N=(24/π)ω，ω为日落时太阳时角，由纬度φ和太阳倾角δ决定：ω=arcos(-tanφtanδ)，δ=0.409 3sin(2πJ/365-1.405)，J为日序数。

2)计算逐月降水与蒸散的差值

Di=Pi-EP(i)

(2)

式中，Di为第i个月的净降水量，mm。不同时间尺度的Di为：

(3)

式中k为月时间尺度。

3)计算Di的累积概率

采用3参数对数逻辑斯特分布(Log-Logistic)拟合序列Di，其分布函数为：

F(x)= 1/(1 + (α/(x-γ))β)

(4)

式中α、β和γ分别为尺度、形状和位置参数，由概率权重矩法估计：

α=(w0-2w1)β/[Г(1+1/β)Г(1-1/β)]，

β=(2w1-w0)/(6w1-6w0w2)，γ=w0-Г(1+1/β)Г(1-1/β)，wk为k阶样本概率权重矩，k=0，1，2…。

4)累积概率标准正态化

净降水量服从的Log-Logistic分布为偏态分布，将偏态分布累积概率值转换为标准正态分布：

z=W-(c0+c1W+c2W2)/

(1+d1W+d2W2+d3W3)

(5)

式中，z为标准正态化后的SPEI值；c0=2.515517；c1=0.802853；c2=0.010328；d1=1.432788；d2=0.189269；d3=0.001308；当净降水量累积概率F≤0.5时，W= (-2ln(1-F))1/2，当F>0.5时，W= (-2ln(F))1/2，相应的z值取相反数。

表1 SPEI干旱等级划分

由于SPEI 通过概率密度函数求解累积概率，再将累积概率标准正态化而得，消除了降水和气温的时空分布差异，在不同区域和时段均能有效地反映旱涝状况。与SPI一样，SPEI是基于概率计算得到的，因此SPI的干旱等级划分标准SPEI同样适用，根据中华人民共和国《气象干旱等级》[16]国家标准来划分干旱等级，如表1所示。

SPEI可根据不同尺度进行计算，一般有1、3、6、12个月时间尺度。由于北江流域一年中降水主要集中在汛期(4-9月)，汛期又是温度较高的夏半年，蒸发旺盛，非汛期(10月-次年3月)降水较少，蒸发较弱，时间尺度大致为6个月，因此为较好的识别干旱情况，本文选用6个月时间尺度的SPEI。

1.2 干旱识别与干旱变量的定义

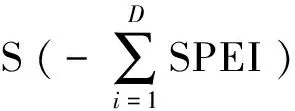
图2 游程理论识别干旱变量示意图

1.3 干旱变量边缘分布

一般来说，对于干旱历时而言，如果作为离散型分布，可用几何分布拟合[18]，如果作为连续型分布，常用指数分布进行拟合[17]，结合当前国内外的研究情况，本文采用指数分布对干旱历时进行拟合。在干旱烈度和烈度峰值的拟合上，本文选用气象水文学领域常用的指数分布(两参数，即2P，下同)、标准耿贝尔分布(2P)、伽玛分布(皮尔逊 Ⅲ型，3P)、广义极值分布(3P)、广义逻辑斯特分布(3P)、对数逻辑斯特分布(3P)、对数正态分布(3P)、广义帕累托分布(3P)、韦克比分布(5P)、维布尔分布(3P)、锐利分布(2P)共11种分布函数对18站进行拟合。统一采用线性矩法估计参数[19]，通过Kolmogorov-Smirnov(K-S)法进行优度检验[20]，并确定出最佳的分布函数，进而运用Copula函数构建联合分布。

1.4 Copula函数定义

1.5 Copula函数的选择与参数估计

本文根据Genest和Rivest[21]提出的理论估计值-经验估计值关系图法来评价和选择Copula。采用Kendall秩相关系数τ[14]度量连接函数的相关性，并利用相关系数τ计算出二维Archimedean Copula函数的参数值。

Shiau和Shen[22]推导出了干旱变量联合重现期上(T0)和同现重现期(Ta)的计算公式：

T0(x,y) =E(L)/P[X>xorY>y] =

E(L)/[1-C(FX(x),FY(y))]

(6)

Ta(x,y) =E(L)/P[X>x,Y>y]

=E(L)/[1-FX(x)-FY(y)+C(FX(x),FY(y))]

(7)

式中，E(L)为干旱间隔期望值(即非干旱历时与干旱历时期望值之和)。变量X和Y的重现期(即边缘重现期)计算公式为：

T(x) =E(L)/[1-FX(x)]；

T(y) =E(L)/[1-FY(y)]

(8)

以上计算过程均采用Matlab软件编程实现，部分代码由http://code.google.com/p/copula/网站免费获得。

2 结果与分析

2.1 边缘分布函数结果分析

2.1.1 概率分布函数选择 研究结果表明(表2所示)，干旱烈度的拟合中两参数的锐利分布、指数分布、标准耿贝尔分布拟合较差，分别有83.3％、55.6％、16.7％的站没有通过检验(0.05置信水平，下同)，其它分布除对数正态分布(3P)有1个站(仁化)没有通过检验外，其余都通过了检验，根据K-S D统计值越小拟合越优原则，可以看出维布尔分布(3P)、韦克比分布(5P)、伽玛分布(3P)、对数正态分布(3P)和广义帕累托分布(3P)在大部分站点拟合较好，其中维布尔分布(3P)在大多数站点拟合最优。烈度峰值的拟合中(由于篇幅所限，不再以表格形式列出)，18站在所有分布函数中都能通过0.05临界值检验，其中维布尔分布(3P)和韦克比分布(5P)在大部分站点拟合较好，而广义帕累托分布(3P)在大多数站点拟合最优。

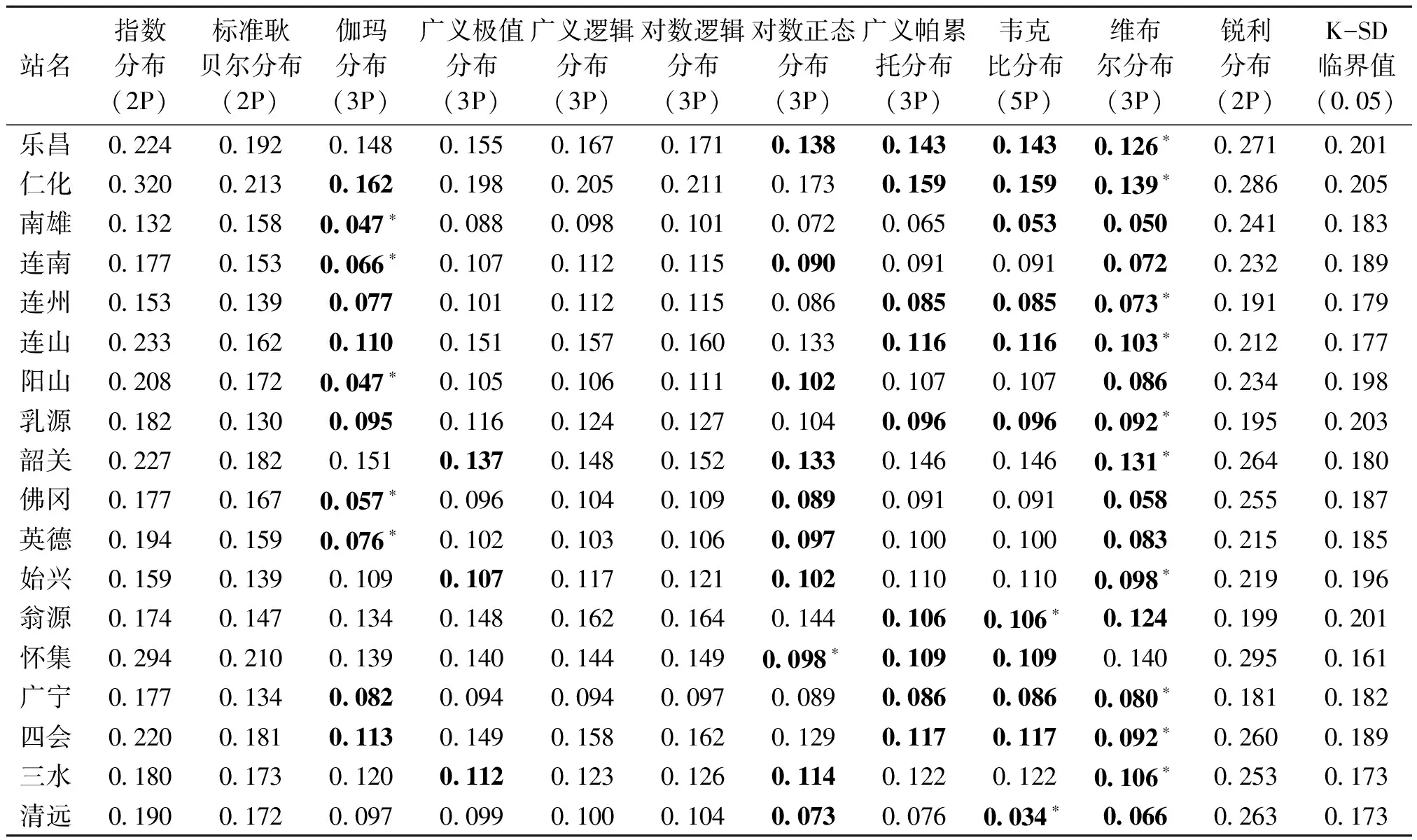
表2 干旱烈度11种概率分布的K-S D统计量1)

1)加粗的为拟合较好的前3种分布函数，标*的为拟合最好的概率分布(也是本文采用的概率分布)。

2.1.2 干旱变量10a重现期设计值空间分布 表3为根据上述拟合最好的概率分布函数推断出的干旱烈度(S)、烈度峰值(P)及干旱历时(D，指数分布)5、10、20、50、100 a一遇设计值(只列出了韶关站数据)；这里主要分析干旱历时、烈度和烈度峰值10年一遇设计值的空间分布情况(图3所示，采用样条函数法[23]插值，该方法的优点是能够准确的通过样点拟合出连续光滑的表面)。

表3 韶关站各重现期对应的干旱变量设计值及联合分布的重现期

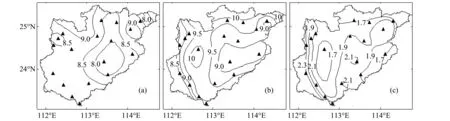
图3 干旱历时(a)、烈度(b)及烈度峰值(c)10年一遇设计值空间分布

流域干旱历时10 a重现期设计值(图3a)最大值为始兴9.3月，最小值为英德7.7月，其余各站均介于8-9月之间，流域18站平均为8.5月；总体来看流域内部区域差异并不明显，但平均8.5月的干旱历时说明流域面临干旱历时较长的风险较大。

干旱烈度10 a重现期设计值(图3b)最大值(10.13)位于阳山，其余各站均介于8.5～10.0之间，平均值为9.19；总体来看，流域中部偏西及北部边缘(阳山、乐昌、仁化等地区)为高值区域，东部的英德、翁源地区为低值区域。

烈度峰值10 a重现期设计值(图3c)最小值为1.62(阳山站)，连山、英德、始兴、怀集、广宁、三水、清远7站(占流域18站38.89％)设计值在2.0以上，18站平均值为1.96；从中可以看出流域18站10年一遇设计值均达到重旱以上级别，平均值接近特旱级别，38.89％的站达到特旱(等级划分标准见文献[13，16])级别；空间分布趋势表现为西南部边缘及东部为高值区域，中部偏西及北部边缘为低值区域。

2.2 二维联合Copula函数结果分析

2.2.1 Copula函数的选择与参数估计结果分析 计算发现18站干旱历时、干旱烈度、烈度峰值两两之间的Kendall秩相关系数τ分别介于0.789～0.903、0.519～0.706、0.673～0.848之间，说明干旱变量之间具有较高的相关性。由于AMH Copula函数不适用于高的正或负相关性，只有Kendall系数-0.1817<τ<1/3时才适用，而本研究中的随机变量Kendall系数均超过1/3，故不适用于AMH Copula函数。

由Genest-Rivest检验法[21]计算的Kc(t)-Ke(t)关系图(图4只列出了韶关站Kc(t)-Ke(t)关系图)发现，18站干旱历时-烈度、历时-烈度峰值均表现为GH Copula函数图上的点最接近45°对角线，即GH Copula拟合最优；18站烈度-烈度峰值Kc(t)-Ke(t)关系图中，GH Copula、Clayton Copula函数图上的点均分布在45°对角线附近，其中8站表现为GH Copula函数图上的点最接近45°对角线，10站表现为Clayton Copula函数图上的点最接近45°对角线。在干旱风险分析中，人们更关心的是随机变量的尾部相关性，也就是当一个随机变量取较大的值或者较小的值时，它对另一个随机变量的取值是否有影响。根据干旱的理论知识可知，干旱历时的长短是干旱烈度及烈度峰值的重要原因，由于干旱具有连续性的累积效应，一般来说干旱历时越长，烈度越大，旱情越严重，对应的烈度峰值也会越大；结合干旱的风险评估，人们更关注干旱历时、烈度、烈度峰值之间的上尾相关性，因此在烈度-烈度峰值GH Copula与Clayton Copula的对比中本文选取具有上尾相关性的GH Copula作为联接函数。然后采用相关性指标法估计联接函数的参数θ，即运用Kendall秩相关系数τ与GH Copula参数θ之间的关系(τ=1-1/θ)计算。

图4 韶关站Genest-Rivest方法检验结果

2.2.2 Copula两变量重现期和风险分析 表3列出了韶关站5、10、20、50、100年重现期对应的干旱变量二维联合分布(D-S、D-P、S-P)的联合重现期(T0)和同现重现期(Ta)，本文主要分析流域50和100 a的情况(图5，采用样条函数插值法[23])。

从图5可以看出，流域D-S50、100 aT0(图5a1、a2)及Ta(图5 b1、b2)、D-P50、100 aT0(图5c1、c2)、S-P50、100 aT0(图5e1、e2)具有比较相似的空间分布趋势，均主要表现为西部(连南、连山、怀集、广宁一带)、南部(三水、清远地区)及北部的始兴地区为相对低值区域，中北部的阳山、乐昌、仁化及东部的翁源地区为相对高值区域。D-P50、100 aTa(图5d1、d2)、S-P50、100 aTa(图5f1、f2)具有比较相似的空间分布趋势，虽然低值区域仍然为西部、南部及北部的始兴地区，但其高值区域范围明显扩大，北部(乐昌、南雄地区)、东部(翁源、佛冈地区)及中部的乳源、韶关、英德地区均为高值区域。可以看出，流域西部(连南、连山、怀集、广宁一带)、南部(三水、清远地区)及北部的始兴地区出现其中之一(即干旱历时长或烈度大或烈度峰值大)或其中两者同时出现的概率均较大，从而具有较大的干旱风险；相对而言，流域中北部(阳山、韶关、乐昌等地)及东部的翁源等地干旱风险较小。

从流域18站平均值来看，D-S50、100 aT0平均值分别为42.3、84.5 a，Ta平均值分别为52.1和104.0 a；D-P50、100 aT0平均值分别为35.3和70.4 a，Ta平均值分别为69.2和138.9 a；S-P50、100年T0平均值分别为39.0、78.4 a，Ta平均值分别为57.7、115.9 a。从最大值最小值来看，D-S、D-P及S-P50、100 aT0最小值均位于怀集，最大值均位于阳山；D-S、D-P及S-P50、100 aTa最小值均位于怀集，最大值均位于翁源。从中可以看出，整个流域出现干旱历时长或烈度峰值大的概率较大，出现干旱烈度大或烈度峰值大的概率也较大，其中怀集出现以上各种干旱情况的概率最大。

图5 广东北江流域干旱变量联合分布重现期空间分布

3 结 论

本文基于SPEI指标对广东北江流域18站近50 a干旱单变量概率分布和两变量Copula联合分布进行研究，主要得到以下结论：

1) 干旱烈度的拟合中两参数的锐利分布、指数分布拟合较差，韦克比分布(5P)、伽玛分布(皮尔逊Ⅲ，3P)、对数正态分布(3P)和广义帕累托分布(3P)在大部分站点拟合较好，维布尔分布(3P)在大部分站点拟合最优；烈度峰值的拟合中，维布尔分布(3P)和韦克比分布(5P)在大部分站点拟合较好，广义帕累托分布(3P)在大部分站点拟合最优。

2) 干旱历时十年一遇设计值区域差异不明显，平均值为8.5月，说明整个流域面临干旱历时较长的风险较大。流域18站烈度峰值十年一遇设计值均达到重旱以上级别，平均值接近特旱级别，近40％的站达到特旱级别；由于烈度峰值是干旱程度的极端表现，以上结论说明流域在极端干旱上形势严峻。

3) 从流域50、100年重现期对应的干旱变量二维联合分布的联合重现期和同现重现期来看，流域西部(连南、连山、怀集、广宁一带)、南部(三水、清远地区)及北部的始兴地区出现其中之一(即干旱历时长或烈度大或烈度峰值大)或其中两者同时出现的概率均较大，从而具有较大的干旱风险；相对而言，流域中北部(阳山、韶关、乐昌等地)及东部的翁源等地干旱风险较小。

参考文献：

[1]WIHITE DA.Drought as a Natural Hazard:Concepts and Definitions[M]//WIHITE D A,Ed.Drought:A Global Assessment.Routledge,2000:3-18.

[2]国家科学技术委员会．中国科学技术蓝皮书第5号《气候》[M]．北京：科学文献出版社，1990.

[3]中国气象灾害大典·广东卷[M].北京:气象出版社,2006:6,204-206.

[4]MISHRA ASHOK K,SINGH VIJAY P.A review of drought concepts[J].Journal of Hydrology,2010,391:202-216.

[5]黄晚华，杨晓光，李茂松,等．基于标准化降水指数的中国南方季节性干旱近58a演变特征[J]．农业工程学报，2010，26(7):50-59.

[6]陈子燊，黄 强，刘曾美．1962-2007年广东干湿时空变化特征分析[J]．水科学进展，2013，24(4):469-476.

[7]江 涛，杨 奇，张 强,等．广东省干旱灾害空间分布特征[J]．湖泊科学，2012，24(1):156-160.

[8]McKEE TB，DOESKEN NJ，KLEIST J．The relationship of drought frequency and duration to time scales[C]//The 8th Conference on Applied Climatology，Anaheim，CA，1993:179-184.

[9]HU Q,WILLSON G D.Effect of temperature anomalies on the Palmer drought severity index in the central United States[J].International Journal of Climatology,2000,20,1899-1911.

[10]VICENTE-SERRANO SM,BEGUERíA S,LóPEZ-MORENO JI.A multiscalar drought index sensitive to global warming:The standardized precipitation evapotranspiration index[J].Journal of Climate,2010,23(7):1696-1718.

[11]CAI W，COWAN T．Evidence of impacts from rising temperature on inflows to the Murray-darling basin[J]．Geophysical Research Letters，2008，35:L07701．[doi:10．1029/2008GL033390].

[12]LORENZO-LACRUZ J，VICENTE-SERRANO SM，LPEZ-MORENO J I，et al．The impact of droughts and water management on various hydrological systems in the headwaters of Tagus River (central Spain) [J]．Journal of Hydrology，2010，386:13-26.

[13]刘占明，陈子燊，黄 强，等．7 种干旱评估指标在广东北江流域应用中的对比分析[J]．资源科学，2013，35(5):1007-1015.

[14]NELSEN RB.An Introduction to Copulas [M].New York:Springer,2006.

[15]EMIR Z,ATILA S.A method of streamflow drought analysis [J].Water Resources Research,1987,23(1) :156-168.

[16]气象干旱等级 [S].GB/T20481-2006.

[17]SHIAU JT.Fitting drought duration and severity with two-dimensional Copulas[J].Water Resources Management,2006,20:795-815.

[18]MATHIER L,PERREAULT L,BOBE B.The use of geometric and gamma-related distributions for frequency analysis of water deficit[J].Stochastic Hydrology and Hydraulics,1992,6(4):239-254.

[19]HOSKING JRM.L-Moments:Analysis and estimation of distributions using linear combinations of order statistics[J].Journal of the Royal Statistical Society,1990,52(1):105-124.

[20]FRANK J,MASSE J.The Kolmogorov-Smirnov test for goodness of fit[J].Journal of the American Statistical Association,1951,46(253):68-78.

[21]GENEST C，RIVEST L．Statistical inference procedures for bivariate Archimedean copulas[J]．Journal of American Statistical Association，1993，88:1034-1043.

[22]SHIAU JT,SHEN HW.Recurrence analysis of hydrologic droughts of differing severity[J].Journal of Water Resources Planning and Management,2001,127(1):30-40.

[23]FRANRE R.Smooth interpolation of scattered path by local thin plate [J].Comp Maths with Appls Great Britain,1982,8(4):237-281.