及时支护隧洞变形规律研究及稳定性评价
刘乃飞,李 宁,2,郭晓刚
(1. 西安理工大学岩土工程研究所,陕西西安 710048; 2. 中国科学院寒区旱区环境与工程研究所冻土工程国家重点实验室,甘肃兰州 730000; 3. 奥地利维也纳农业大学,维也纳维也纳 999013)
随着我国经济建设的蓬勃发展,水电、金属矿山、交通运输等各行业均取得了举世瞩目的成绩[1],并逐渐将工程建设场所转向水文工程地质比较恶劣的地区,特别是在软岩及土质地区修建了一大批隧洞工程。据不完全统计,仅近10年新增的输水隧洞中,软岩隧洞就占新增隧洞总长的24.0%[2]。根据国际岩石力学学会的定义,软岩是指单轴抗压强度在0.5~25 MPa之间的一类岩石[3],具有强度低、遇水易软化和稳定性差等特点。在软岩中开凿地下洞室,最主要的问题就是解决施工过程中的安全问题,保证施工过程中的围岩稳定,减少塌方,避免人员伤亡和财产损失。然而实际上在软岩或土质地层修建地下洞室的过程中均发生过不同程度塌方事故,这逐渐引起了科研人员的关注,软岩隧洞的变形特征和稳定性问题开始得到研究。付敬等[4]采用三维黏弹塑性数值方法研究了围岩的流变特性与时效变形。刘小伟等[5]研究了浅埋红层软岩隧洞的变形和应力变化特征。李叶等[6]通过原位测试、室内试验和监测手段研究了软质围岩变形特征和机理。曹东杰[7]对穿越软岩等复杂地质条件下隧洞支护体系的受力特性及其稳定性进行了评估。张鹏等[1]结合工程经验建立了隧洞顶拱变形与塑性区、松动区半径大小的关系式。杜守继[8]和焦苍等[9]采用有限差分软件分别研究了软岩隧洞受力变形特征和软弱围岩在开挖过程中的大变形机理。黄林伟等[10]从软岩隧洞开挖和支护两个方面探讨了软岩隧洞变形机理。戴宏亮等[11]分析推导了软岩隧洞锚固区流变问题的理论模型和解法。李鸿博[12]、张青龙[13]等对软岩隧洞变形的空间效应和时间效应进行了研究,并分析了软岩隧洞的变形机理。上述研究成果为我国隧道工程建设的顺利开展做出了巨大贡献,但这些研究工作多服务于具体的工程项目,且没有给出及时支护情况下软岩隧洞的应力和变形规律,因此开展具有普遍意义的需及时支护隧洞的变形规律及稳定性方面的研究尤为重要。
本文通过设定详尽的数值试验方案分别研究在不同洞径、不同埋深、不同强度参数和不同弹性参数等条件下需及时支护的软岩或土质隧洞围岩拱顶变形和顶拱喷层应力的相互关系,进而探讨以支护结构安全性为参考标准的及时支护隧洞围岩稳定性评价新理念,并将其成功应用于新疆库尉输水工程,以期为在软弱地层中开挖的隧洞工程的设计和施工提供理论指导。
1 数值模型及研究方案
1.1 数值分析模型

图1 数值分析模型Fig.1 A numerical calculation model
本文采用的数值分析模型如图1所示,模型中采用三角形六节点等参数实体单元模拟围岩,将其视为理想弹塑性体。锚杆用Bolt单元模拟,喷层单元用Beam单元模拟。屈服准则为Mohr-coulomb准则,数值模型边界条件为:底部固定端约束,两侧法向约束。
1.2 数值试验方案
实际工程中,围岩类别、断面尺寸、埋深及支护措施等均对围岩变形产生较大影响,致使喷层受力也存在显著差异。本文根据工程实际,选取力学性质较弱,施工过程中需及时支护的围岩类别,分析各参数对围岩变形与喷层应力对应关系的影响。具体研究方案如表1所示。

表1 数值试验方案参数Tab.1 Parameters of numerical experiment scheme
注: 支护方案根据喷锚规范选定。
2 及时支护隧洞变形规律研究
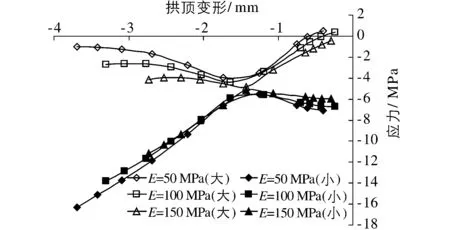
图2 变形模量影响曲线Fig.2 Influence curves of deformation modulus
软岩及土质隧洞由于具有强度低及变形大的显著特点,致使开挖隧洞时需及时施做支护结构,限制围岩变形、确保工程安全。然而对于已施做支护结构的隧洞的变形,目前尚未明确允许变形标准(传统方法等均是基于毛洞提出的)。因此,本节采用拟定的试验方案研究及时支护隧洞拱顶围岩在施做支护后发生的变形和喷层拱顶应力值的对应关系。
2.1 变形模量影响
图2为变形模量对拱顶围岩变形和喷层应力对应关系影响曲线,从图中可见各变形模量情况下喷层大、小主应力均随围岩变形呈近抛物线型变化,大主应力对模量变化较小主应力更敏感。变形较小时,大主应力(绝对值)随变形的增加而增大,当变形达到一定值后,则出现相反的情况,且变化速率也逐渐减缓。而小主应力则呈现出与大主应力近似相反的规律。相同围岩变形条件下,喷层大主应力随模量的增大而增大,小主应力则随模量的增大而减小。不同变形模量条件下,各曲线的极值点近似出现在同一位置,对应的变形量约为1.4 mm。
2.2 泊松比影响

图3 泊松比影响曲线Fig.3 Influence curves of Poisson′s ratio
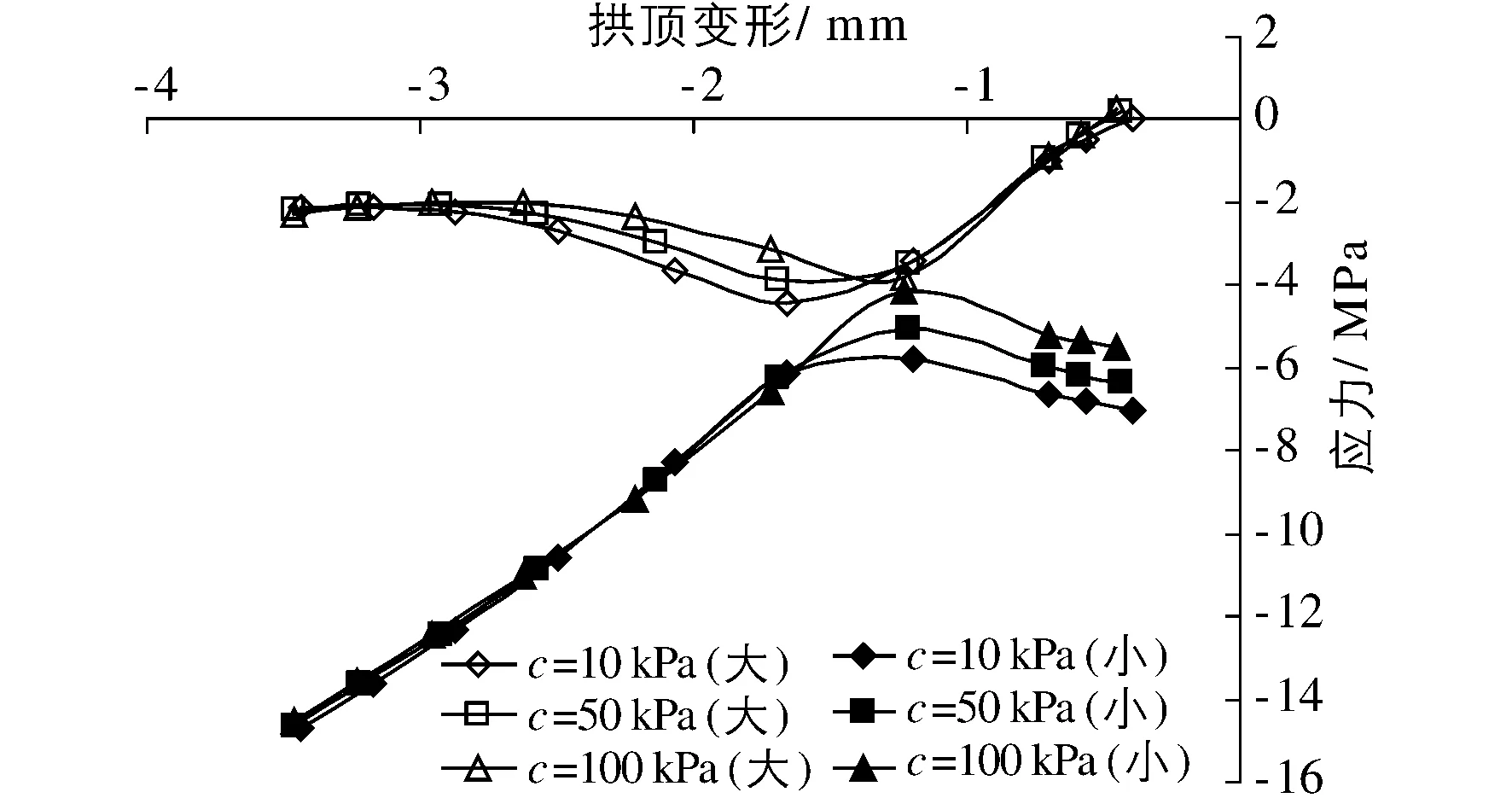
图4 黏聚力影响曲线Fig.4 Influence curves of cohesion
泊松比对喷层拱顶大、小主应力的影响和变形模量类似,关系曲线均为抛物线型且对大主应力的影响更为明显。变形相同时,大主应力随泊松比的增大而增大。但图3表明,不同泊松比情况下,曲线极值对应的变形量有较大区别,即泊松比越大,拱顶处的变形值也越大。对于最小主应力,泊松比的影响十分有限,且呈现出与大主应力相反的变化规律。泊松比和侧压力系数密切相关,在城门洞形情况下,倘若喷层的刚度相对围岩较大,边墙变形将会使拱顶处喷层受挤压而有向上隆起的趋势。这种类似预应力的效果使得这时的喷层能承受较大的拱顶围岩压力而不出现拉应力,即拱顶喷层的环向应力需在较大竖向压力作用下才能实现由压应力到拉应力的转化。
2.3 黏聚力影响

图5 内摩擦角影响曲线Fig.5 Influence curves of internal friction angle
由图4可知,黏聚力对大主应力的影响在小变形时并不明显,各曲线几乎重合,应力随变形的增加而增大。变形值增大到约1.5 mm后出现拐点;此时各曲线出现明显差别,变形相同时,黏聚力越大则喷层内的大主应力越小,且随着黏聚力的增大极值点逐渐远离原点。黏聚力对最小主应力的影响效果出现和最大主应力相反的情况,在变形较小时各曲线之间的差值明显,且黏聚力越大时相同变形的最小主应力越小,而在较大变形时各曲线几乎重合。
2.4 内摩擦角影响
图5表明内摩擦角对关系曲线的影响较前几个因素有明显不同,不同内摩擦角条件下曲线极值点存在较大分散性,内摩擦角越大,极值点对应变形量越小。内摩擦角对大主应力的影响明显大于小主应力,且变形较小时大主应力随内摩擦角的增大而增大,小主应力随内摩擦角的增大而减小。
2.5 洞径和埋深的影响
图6表明洞径对各主应力均有显著影响,大主应力随变形呈先增大后减小,而小主应力则表现为先减小后增大的趋势。从图中可见曲线顶点随半径的增大逐渐远离原点,即隧洞半径越大极值点对应的变形量也越大,变化曲线也越宽浅,且相同洞径条件下,大、小主应力曲线的顶点十分接近。
由图7可知,不同埋深条件下大、小主应力的变形均近似呈抛物线型,且变形较小时小主应力随埋深的增大而增大,变形较大时大主应力随变形的增大而增大。埋深增大的影响效果和内摩擦角减小的影响效果相类似,随埋深的增大,大小主应力曲线顶点对应的变形值也相应增大。

图6 洞径影响曲线 图7 埋深影响曲线 Fig.6 Influence curves of tunnel diameter Fig.7 Influence curves of embedded depth of tunnel
2.6 侧压力系数影响

图8 侧压力系数影响曲线Fig.8 Influence curves of lateral pressure coefficient
由图8可知侧压力系数的影响应按侧压力系数大于和小于1两种情况来分析。侧压力系数小于1时,大、小主应力变化曲线均存在极值点,较大的侧压力系数对应较大的边墙变形,倘若喷层的刚度远大于围岩的刚度,边墙的变形将会使拱顶处喷层受挤压而有向上隆起的趋势。所以,侧压力系数较大时,最大主应力的曲线顶点对应的变形值较大。当侧压力系数大于1时,由于边墙对喷层的挤压作用很强,大、小主应力变化曲线均不存在极值点,随变形的增加应力不断增大,若最小主应力达到喷层的抗压强度时,变形还继续发展,喷层就会开裂破坏。
3 及时支护隧洞稳定性评价方法
3.1 稳定性评价新方法
影响喷层应力的因素非常多,因此,本节根据上一节研究结论并结合工程实际,选取原计算方案中的部分方案,对通过支护结构安全性来判断隧洞围岩稳定性的新方法进行详细分析。选取的分析方案见表2。

表2 数值试验方案参数Tab.2 Parameters of numerical experiment scheme
通常情况下,拱顶围岩变形均为竖直向下变形,拱部喷层较容易发生拉裂破坏,但当侧压力系数较大时,拱顶喷层也存在受压破坏的可能。因此,本文将综合考虑喷层施做后拱顶的围岩变形与喷层主应力之间对应关系,推算出喷层既不产生拉破坏也不产生压破坏的围岩变形范围。将各方案结果整合,可得围岩变形与喷层应力关系曲线(见图9)。
需要说明的是,图9中的最大主应力和最小主应力只是以变形发展初期的应力大小来定义的,后期由于应力调整,应力主轴对调,大、小主应力名称发生了互换。
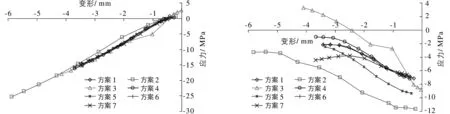
(a) 大主应力 (b) 小主应力图9 各方案围岩变形与喷层应力对应关系曲线Fig.9 Relationship curves between deformation and principal stress of each alternative
由于各计算方案中围岩参数及支护参数均为确定的值,变形发展的结果也是确定的,各方案喷层均未达到其设计强度。由图9可见,各曲线基本呈线性发展,可进行线性拟合,最小主应力在曲线末端逐渐趋于平缓,拟合的曲线对应设计抗拉强度的变形值偏小,工程应用中偏于安全。拟合的曲线公式及对应喷层设计强度的变形值见表3。
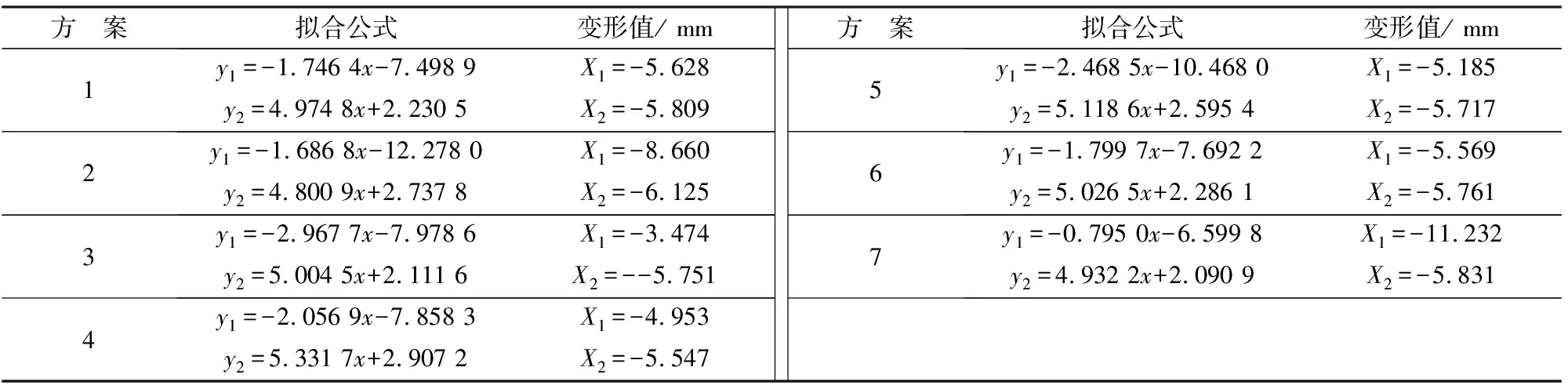
表3 拟合公式及喷层设计抗拉(压)强度对应的变形值Tab.3 The fitting formulas and maximal deformation
注:y1为抗拉强度,y2为抗压强度;应力以拉为正,压为负;变形以向洞内变形为负。
确定支护结构安全需同时满足喷层内的最大压应力小于其设计抗压强度和最大拉应力小于其设计抗拉强度,即取以上分析结果的较小值作为判断标准。根据以上分析最终确定各方案允许变形量见表4。

表4 基于喷层强度确定的拱顶围岩允许变形Tab.4 Surrounding rock maximal deformation based on the design strength of shotcrete
3.2 评价方法验证
对库尉输水工程进行为期2年的安全监测。该工程位于巴音郭楞蒙古自治州开都河至孔雀河流域境内,主要任务是为库尔勒市经济技术开发区供水,全长13.7 km。从桩号1+130.0 m至4+200.0 m洞段设计开挖断面为城门洞型,主要围岩类型为低液限粉(黏)土、粉土夹砂砾层以及粉细砂夹砾石,围岩类别差,需及时支护。本文选取该工程1+200.2 m和2+238.0 m的两个断面作为算例来验证该评价方法的可靠性。
(1)1+200.2 m断面 该断面埋深20 m,于2010年10月31日施做支护,支护措施为立钢格栅拱架,20cm厚喷层,并施做系统锚杆。断面参数为侧压力系数λ=0.70,变形模量E=0.08 GPa,泊松比μ=0.32,内聚力C=0.02 MPa,摩擦角Φ=32°。监测从2010年10月30日开始。
整理该断面测量数据可得掌子面推进过程中拱顶沉降量为2.51 mm,从而推求得到喷层施做后围岩总变形为3.07 mm。根据本文研究结果推算拱顶允许变形为5.6 mm,则可以确定该断面支护结构安全。由位移释放过程曲线推求得到围岩最终总变形为13.35 mm,而由芬纳公式求得的允许变形值为40.46 mm,即围岩处于稳定状态,后续的测量及观察证明了该结论。

图10 初期支护局部裂缝Fig.10 Local failure of the primary support
(2)2+238.0 m断面 该断面埋深53 m,于2010年11月13日施做支护,支护措施为立钢拱架,15 cm厚喷层,并施做系统锚杆。断面参数为侧压力系数λ=1.0,变形模量E=0.04 GPa,泊松比μ=0.35,内聚力C=0.02 MPa,摩擦角Φ=37.5°。监测从2010年11月13日开始。
整理该断面测量数据可得掌子面推进过程中拱顶沉降量为4.98 mm, 推求可得喷层施做后围岩总变形为5.48 mm。根据本文研究结果推算拱顶允许变形为4.65 mm,表明该断面围岩已处于不稳定状态,现场观察发现该断面喷层多处出现了裂缝(见图10)。
4 结 语
本文根据软岩及土质隧洞开挖施工过程中易出现大变形和塌方等工程问题及现有围岩稳定性评价方法存在的不足,选取需及时支护的隧洞作为计算方案进行数值试验,研究了该类隧洞拱顶围岩变形和喷层应力的相互关系,探讨了该类隧洞围岩稳定性评价的新方法,主要取得以下几点认识:
(1)随着变形的发展,喷层拱顶处最初的大主应力逐渐减小,小主应力逐渐增大,变形发展到一定值时两者名称发生互换。
(2)各因素对拱顶围岩变形和喷层应力有显著影响。变形模量和泊松比对喷层主应力的影响规律基本相同,大主应力随该两因素的增大而增大;而黏聚力和内摩擦角对其影响却表现出相反的情况。
(3)针对需及时支护隧洞提出采用数值模拟手段推求确保支护结构安全的拱顶最大变形,并将其作为评价相应洞段围岩稳定性的新方法,采用库尉输水隧洞实测数据验证了该方法的适用性。
(4)本文旨推出基于支护结构安全性来评判需及时支护隧洞围岩稳定性的新理念,对于普遍适用的允许变形量则需要更为全面的计算方案。
参 考 文 献:
[1]张鹏, 李宁, 何敏. 软岩圆形隧洞衬砌支护时机现场变形监测判据研究[J]. 西安理工大学学报, 2007, 23(2): 140-143. (ZHANG Peng, LI Ning, HE Min. Theoretical estimation of the supporting time in soft rocks tunnels under high initial stress[J]. Journal of Xi′an University of Technology, 2007, 23(2): 140-143. (in Chinese))
[2]赵长海, 周小兵, 贺建国, 等. 极软岩隧洞的设计与施工[J]. 岩石力学与工程学报, 2006, 25(增1): 3034-3039. (ZHAO Chang-hai, ZHOU Xiao-bing, HE Jian-guo, et al. Design and construction of tunnel in extremely soft rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(Suppl1): 3034-3039. (in Chinese))
[3]曹玉亮. 软岩隧道围岩稳定性分析与支护研究[D]. 西安: 西安理工大学, 2007. (CAO Yu-liang. Analysis of surrounding rock stability of soft rock tunnel and study on its supports[D]. Xi′an: Xi′an University of Technology, 2007. (in Chinese))
[4]付敬, 董志宏, 丁秀丽, 等. 高地应力下深埋隧洞软岩段围岩时效特征研究[J]. 岩土力学, 2011, 32(增2): 444- 448. (FU Jing, DONG Zhi-hong, DING Xiu-li, et al. A study of aging characteristics of soft surrounding rock in deep tunnel with high ground stress[J]. Rock and Soil Mechanics, 2011, 32(Suppl2): 444- 448. (in Chinese))
[5]刘小伟, 谌文武, 刘高, 等. 引洮工程红层软岩隧洞TBM施工预留变形量分析[J]. 地下空间与工程学报, 2010, 6(6): 1207-1214. (LIU Xiao-wei, CHEN Wen-wu, LIU Gao, et al. Analysis of reserved deformation during the construction of rock-bed soft rock tunnel by TBM in Yintao project[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(6): 1207-1214. (in Chinese))
[6]李叶, 李嘉旭, 宇天奇, 等. 洞松水电站引水隧洞软质围岩变形分析及工程对策[J]. 地质灾害与环境保护, 2012, 23(2): 65-70. (LI Ye, LI Jia-xu, YU Tian-qi, et al. Deformation and engineering measures for soft surrounding rock in the diversion tunnel of Dongsong hydropower station[J]. Journal of Geological Hazards and Environment Preservation, 2012, 23(2): 65-70. (in Chinese))
[7]曹东杰. 软岩隧洞支护体系及施工安全技术研究[D]. 成都: 西南交通大学, 2013. (CAO Dong-jie. Study on support system and safe construction method for soft rock tunnel[D]. Chengdu: Southwest Jiaotong University, 2013. (in Chinese))
[8]杜守继, 职洪涛, 翁慧俐, 等. 高速公路软岩隧道复合支护机理的FLAC解析[J]. 中国公路学报, 2003, 16(2): 70-73. (DU Shou-ji, ZHI Hong-tao, WENG Hui-li, et al. FLAC analysis of composite support mechanism in weak rock tunnel of freeway[J]. China Journal of Highway and Transport, 2003, 16(2): 70-73. (in Chinese))
[9]焦苍, 祝江林, 范鹏, 等. 浅埋软岩隧道开挖围岩变形非线性模拟分析[J]. 地下空间与工程学报, 2005, 1(5): 703-706. (JIAO Cang, ZHU Jiang-lin, FAN Peng, et al. Analysis of the non-linear numerical imitation of surrounding rock deformation during shallow overburden tunnel excavation within soft rock[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(5): 703-706. (in Chinese))
[10]黄林伟, 刘新荣, 杨桦, 等. 软岩隧道不同支护方法的数值分析和效应探讨[J]. 地下空间与工程学报, 2011, 7(1): 77-82. (HUANG Lin-wei, LIU Xin-rong, YANG Hua, et al. Discussion on effects and numerical analysis of different supports to soft rock tunnel[J]. Chinese Journal of Underground Space and Engineering, 2011, 7(1): 77-82. (in Chinese))
[11]DAI H L, WANG X, XIE G X, et al. Theoretical model and solution for the rheological problem of anchor-grouting a soft rock tunnel[J]. International Journal of Pressure Vessels and Piping, 2004, 81(9): 739-748.
[12]李鸿博, 戴永浩, 宋继宏, 等. 峡口高地应力软岩隧道施工监测及支护对策研究[J]. 岩土力学, 2011, 32(增2): 496-501. (LI Hong-bo, DAI Yong-hao, SONG Ji-hong, et al. Construction monitoring for Xiakou soft rock tunnel under high geostress and its supporting measures[J]. Rock and Soil Mechanics, 2011, 32(Suppl2): 496-501. (in Chinese))
[13]张青龙, 李宁, 曲星, 等. 富水软岩隧洞变形特征及变形机制分析[J]. 岩石力学与工程学报, 2011, 30(11): 2196-2202. (ZHANG Qing-long, LI Ning, QU Xing, et al. Analysis of deformation characteristics and mechanism of water-rich soft rock tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(11): 2196-2202. (in Chinese))
[14]桂荣, 刘永. 高应力软岩隧道施工的时空效应分析[J]. 南华大学学报: 自然科学版, 2011, 25(1): 28-32. (GUI Rong, LIU Yong. Analysis of the excavation and support of high stress soft surrounding rock tunnel considering time-space effect[J]. Journal of University of South China(Science and Technology), 2011, 25(1): 28-32. (in Chinese))

