钢筋锈蚀率的概率模型及时变可靠度分析
冯云芬,贡金鑫,杨国平,李荣庆
(1. 大连理工大学土木工程学院,辽宁大连 116024;2. 中交水运规划设计院有限公司,北京 100007)
氯离子环境下钢筋锈蚀是海工混凝土结构性能退化的主要原因。钢筋锈蚀的发展规律一直是混凝土结构耐久性研究的热点[1]。由于诸多因素的影响,混凝土氯离子渗透、钢筋锈蚀呈现高度的随机性。因此,采用随机方法研究氯离子环境下钢筋混凝土构件的性能变化和可靠度是非常必要的。目前,国内外学者已在钢筋混凝土性能劣化和可靠度分析方法方面做了很多的工作[2-8],但这些研究仍不充分,特别是钢筋不同锈蚀阶段的概率特性,需要更深入地研究。
由于随机性的存在,从设计使用年限中某一时刻t来观察,氯离子环境下的钢筋混凝土构件可能处于3种不同状态:钢筋未锈蚀、钢筋已锈蚀但保护层未开裂和保护层已经开裂,时刻t不同,构件处于3种状态的概率就不同。基于这一认识,本文分3种情况建立了钢筋锈蚀率的概率模型,并通过随机分析模拟了t时刻这3种状态出现的概率。基于收集的锈蚀钢筋混凝土梁的试验数据[2-5],建立了剩余承载力与钢筋锈蚀率之间的关系。最后以满足规范中对我国南方海洋环境混凝土结构最低耐久性要求的钢筋混凝土梁为例,进行了时变可靠度分析。
1 构件劣化过程
如图1所示,钢筋锈蚀引起的结构性能退化分为3个阶段。第1阶段为结构建成至钢筋开始锈蚀;第2阶段为钢筋开始锈蚀到混凝土保护层开始出现沿钢筋的纵向裂缝;第3阶段为保护层纵向开裂至结构破坏到不可接受的程度(我国规范JTJ302-2006[8]将钢筋截面损失达10%作为结构功能发生明显退化的标志)。

图1 混凝土构件承载力随时间的变化Fig.1 Load carrying capacity versus service time
1.1 钢筋初锈概率模型
氯离子扩散是一个非常复杂的物理、化学过程,可用Fick第二定律表示:
(1)
式中:C为t时刻深度x处的氯离子浓度(占混凝土质量的百分比);D(t)为时变氯离子扩散系数(m2/s),与时间、温度、湿度和应力水平密切相关,此处表示为:
(2)
式中:D0为某一参考期t0(通常取28 d时的扩散系数(m2/s),D0=10(-12.06+2.4W/C),W/C为水灰比;m为扩散衰减系数,m=0.2+0.4(FA/50+SG/70),其中FA,SG分别为混合物中粉煤灰和矿渣的比例[6];kD,T,kD,H和kD,σ分别为温度、相对湿度和应力水平对氯离子扩散系数的影响因子。
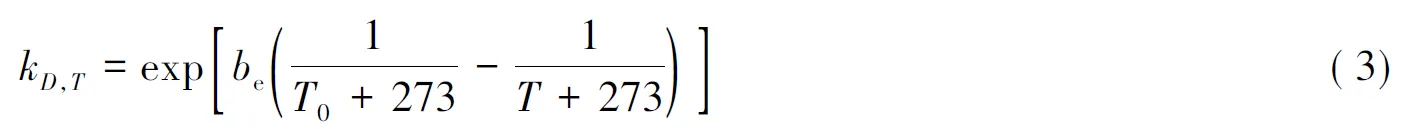
式中:T0为基准温度,一般取20℃;T为混凝土所处环境的温度(℃),取结构所在地平均气温;be为回归系数,基于大量试验,不同混凝土类型对应的be的统计参数[7]如下:普通混凝土的均值和标准差分别为4 500和940;掺加10%粉煤灰混凝土的相应值为2 680和790;掺加30%~50%粉煤灰混凝土的相应值为-4 650和1 725。从统计结果可见服从对数正态分布。
A.V.Saetta等[9]将湿度影响系数kD,H表示为:

式中:Hc为混凝土内部的临界相对湿度,取75%;H为混凝土内部的相对湿度,不同暴露条件下H的取值有所不同,大气区、浪溅区和水位变动区一般可分别取75%,90%和95%[10]。
研究[2,11]表明,系数kD,σ为钢筋应力的3次函数,通过对试验数据的分析,表示为[2]:
(5)
式中:σq为正常使用极限状态准永久组合下的钢筋应力;fyk为钢筋屈服强度标准值;σq/fyk为应力水平。
当氯离子浓度C达到临界氯离子浓度Ct时,钢筋开始锈蚀。由式(1)~(5)得钢筋初锈的时间为:
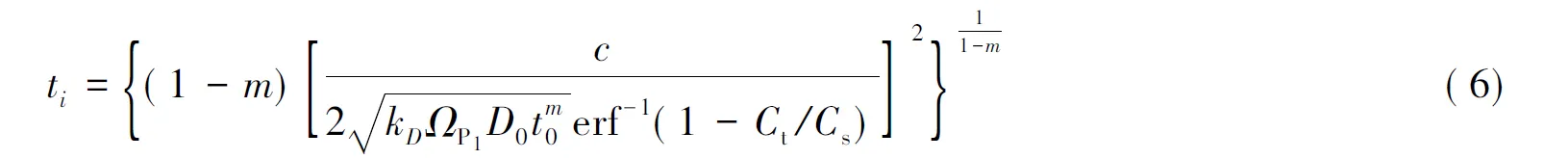
式中:c为混凝土保护层厚度;erf-1(·)为误差函数的反函数;ΩP1为D0的计算模式不定性系数,服从对数正态分布,平均值和变异系数分别为1.168和0.356[6];Cs为表面氯离子浓度,Ct为临界氯离子浓度。
1.2 保护层开裂阶段的概率模型
当钢筋锈蚀深度达到临界锈蚀深度时,混凝土保护层沿钢筋方向发生纵向开裂。若钢筋锈蚀速度为常数,则钢筋开始锈蚀至保护层开裂所经历的时间tc=δcr/λ1,其中δcr为保护层开裂时钢筋的临界锈蚀深度(mm);λ1为保护层开裂前钢筋的锈蚀速度(mm/a)。规范JTJ 302-2006[8]将临界锈蚀深度计算公式表示为:
(7)
式中:d为钢筋直径;fcu为混凝土抗压强度。式(7)的计算值与实测值的比值以Ω2表示,其平均值和变异系数为1.014和0.183[12],服从对数正态分布。
钢筋锈蚀速度一般以腐蚀电流密度表示,本文将保护层开裂前的腐蚀速度表示为:
(8)
式中:腐蚀电流密度的应力影响系数ki,σ=1+1.5(σq/fyk)3≥0.5[2];icorr为钢筋锈蚀电流密度(μm/cm2),可表示为[13]:
(9)
式中:tp为钢筋初锈开始时间;icorr(1)为钢筋初锈时的腐蚀电流密度,icorr(1)=37.8(1-W/C)1.64/c,icorr(1)的模型不定性Ω3的平均值和变异系数分别为1.0和0.2,服从正态分布[14]。
钢筋开始锈蚀后tp时刻钢筋的锈蚀深度为:
(10)
当δav(tp)=δcr时,混凝土保护层沿钢筋方向发生纵向开裂。引入不定性系数ΩP2和ΩP3,从而将钢筋初锈到混凝土保护层开裂时间tc的概率模型表示为:
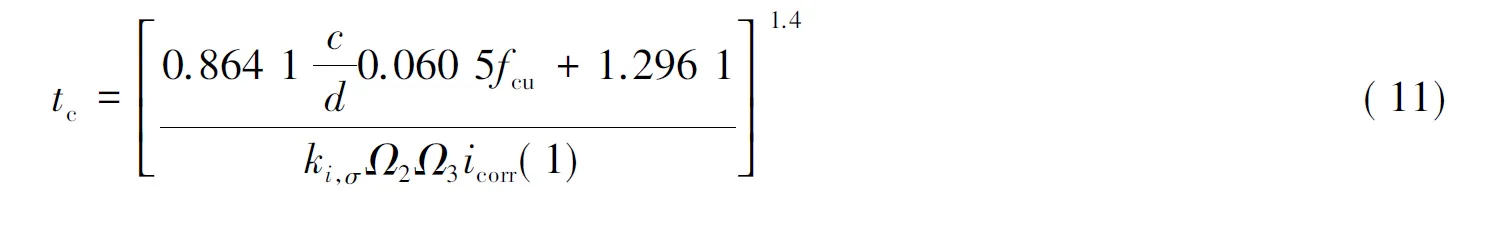
2 钢筋锈蚀率
目前,常用的钢筋锈蚀模型有均匀锈蚀模型和点蚀模型。氯离子引起的钢筋锈蚀一般是点蚀。从承载力的角度考虑,构件的剩余承载力取决于钢筋的最小截面。因此,计算受腐蚀钢筋混凝土构件的剩余承载力,应采用点蚀模型。由于钢筋锈蚀是一个受宏观电流和微观电流耦合控制的过程,实际中无法对其进行区分,因此前面开裂时间计算采用的钢筋锈蚀深度是以宏观电流为基础的。这是因为当钢筋锈蚀率较大时,从宏观上看,仍具有均匀锈蚀的特征。目前,一般由试验结果确定点蚀系数R(最大点蚀深度δmax与均匀锈蚀深度δav的比值),按均匀锈蚀建立锈蚀模型,再确定最大点蚀深度δmax。分析表明[14],最大点蚀深度δmax通常为按均匀锈蚀模型确定的平均锈蚀深度δav的3~9倍。需要说明的是,此处的均匀锈蚀不是传统意义上沿钢筋圆周的均匀锈蚀,而是按一定长度的钢筋锈蚀段确定钢筋的平均锈蚀率。钢筋锈蚀部分实际为月牙形、半圆形或其他形状。本文采用图2所示的点蚀模型。

图2 点蚀模型Fig.2 Corrosion model

图3 t时刻锈蚀率示意Fig.3 Steel bar corrosion rate at time t
t时刻最大点蚀深度δmax(t)与均匀锈蚀深度δav之间存在如下关系[14]:
(12)
式中:R为点蚀系数,认为R服从平均值为5.65、变异系数为0.22的极值Ⅰ型分布[14]。
2.1 钢筋锈蚀深度
钢筋初锈时间ti和混凝土保护层开裂时间ti+tc分别是钢筋开始锈蚀和锈蚀速度加快的转折点,因此,结构性能劣化对钢筋初锈时间ti和混凝土保护层开裂时间ti+tc非常敏感。由于钢筋锈蚀过程存在大量的不确定因素,ti和ti+tc应为随机变量。因此在t时刻进行观察时,可能会存在图3所示的3种情况。因此,本文将ti和ti+tc作为随机变量,分3种情况建立锈蚀率模型,即:t时刻未发生锈蚀(ti>t),t时刻钢筋已锈蚀但混凝土保护层未开裂(ti≤t且ti+tc>t),t时刻混凝土保护层已发生开裂(ti+tc≤t)。
根据图3及前面的公式,t时刻钢筋平均锈蚀深度为:
(13)
由式(12)和(13),t时刻钢筋最大点蚀深度为:
(14)
2.2 钢筋锈蚀率
假设钢筋混凝土构件的钢筋直径相等,则t时刻钢筋的锈蚀率η(t)为:
(15)
式中:A0为钢筋未锈蚀时的截面面积;Apit(t)为点蚀引起的钢筋面积损失,可表示为[14]:
(16)
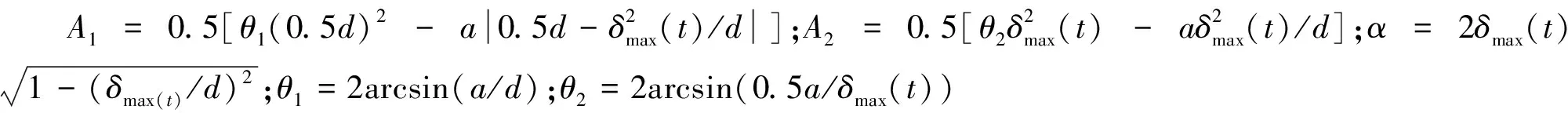
3 钢筋锈蚀率的概率分析
以我国南方海洋环境中满足最低耐久性要求的钢筋混凝土梁为例,对钢筋锈蚀率η(t)进行分析。分析中假设龄期降低系数m=0.6;当前温度T=25 ℃;荷载水平σq/fyk=0.5。
3.1 相关变量统计参数
氯离子侵蚀过程中存在大量的不确定因素,锈蚀率模型中的参数应作为随机变量处理,其标准值和最低耐久性要求如表1所示,统计参数(均值系数k与变异系数δ)和概率分布类型如表2所示。

表1 变量的标准值和最低耐久性要求Tab.1 Characteristic values and minimum durability requirements of variables

表2 各变量的统计参数和概率分布类型Tab.2 Statistical parameters and distribution of variables
3.2 钢筋锈蚀率的概率分布与统计参数
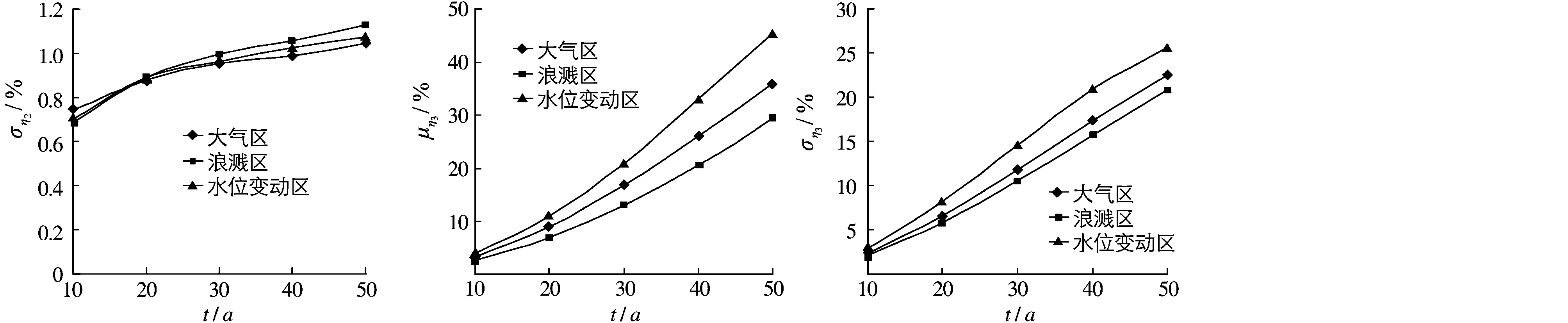
按图4所示流程,采用Monte-Carlo方法模拟确定钢筋锈蚀率η(t)。我国规范规定港口工程结构的设计使用寿命为50年。将[0,50]分为50个时间点,即t=1,2,…,50,对每个时点进行n=100 000次数值模拟,按图5计算锈蚀率的统计参数,其中p1为t时刻钢筋未发生锈蚀的概率(图6(a)),p2,μη2和ση2分别为t时钢筋已锈蚀但保护层未开裂的概率及此种情况下锈蚀率的平均值和标准差(图6(b)(d)(e)),p3,μη3和ση3分别为t时保护层已开裂的概率与此种情况下锈蚀率的平均值和标准差(图6(c)(f)(g))。p1,p2和p3满足p1+p2+p3=1。

图4 钢筋锈蚀率η(t)的计算流程 图5 p1,p2,p3,μη2,ση2,μη3和ση3的计算方法 Fig.4 Calculation flowchart of η(t) Fig.5 Calculation of p1,p2,p3,μη2,ση2,μη3 and ση3
为考虑混凝土抗压强度与水灰比之间的相关性,本文将混凝土抗压强度和水灰比分别表示为:
(17)
式中:μW/C,σW/C和μfcu,σfcu分别为水灰比和混凝土抗压强度的平均值和标准差;Y1,Y2分别为服从标准正态分布的随机变量;ρc为W/C和fcu之间的相关系数,此处取为-0.8。
Monte-Carlo模拟得到的p1,p2,p3,μη2,ση2,μη3和ση3与时间的关系如图6所示。由图6(a)~(c)可看出,钢筋未锈蚀的概率p1和钢筋已锈蚀但保护层未开裂的概率p2随观察时刻t的增加而减小,混凝土保护层发生开裂的概率p3随观察时刻t的增加而增大。锈蚀率的平均值和标准差μη2,μη3和ση2,ση3随观察时刻t的增加而增大。
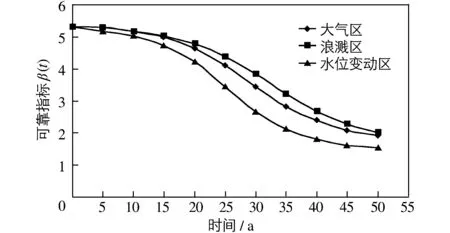
以50年为例,此时锈蚀率的直方图和拟合的概率密度曲线如图7所示。从图中可看出,锈蚀率服从双峰分布。概率密度曲线的2个峰分别表示ti≤t (18) (a) p1随时间变化 (b) p2随时间变化 (c) p3随时间变化 (d) μη2随时间变化 (e) ση2随时间变化 (f) μη3随时间变化 (g) ση3随时间变化图6 锈蚀率统计参数与时间的关系Fig.6 Statistical parameters of corrosion rate versus time 从而,钢筋锈蚀率η(t)的概率分布函数为: (19) 式中:Fη2(x)和Fη3(x)分别为与fη2(x)和fη3(x)对应的概率分布函数。分析表明,Fη2(x)和Fη3(x)均可用正态分布描述,如图7所示。 (a) 大气区 (b) 浪溅区 (c) 水位变动区图7 50年时锈蚀率的概率分布Fig.7 Histograms of corrosion rate of 50 years 钢筋混凝土结构构件的时变抗力通常表示为: 图8 抗力衰减函数与钢筋锈蚀之间的关系Fig.8 Relationship between g(t) and η(t) (20) 式中:R(t)为构件t时刻的抗力;R0为构件钢筋未锈蚀时的抗力;g(t)为抗力衰减函数。 对文献[2-5]的试验数据进行分析,抗力衰减函数g(t)表示为: (21) 式(21)计算结果与试验结果的比较见图8。试验值与式(21)计算值比值Ω4的平均值和标准差分别为1.008和0.045,服从对数正态分布。 可靠度分析中仅考虑永久荷载与码头堆货荷载相组合的情况,则时变功能函数为: (22) 式中:SG,SQ分别为永久荷载效应和可变荷载效应。结构可靠指标的大小与荷载效应的具体取值无关,仅与荷载效应比值ρ=SQk/SGk有关,此处假设ρ=2.5。受弯构件抗力R0的统计参数k=1.321,δ=0.112,呈对数正态分布;永久荷载SG的统计参数k=1.02,δ=0.04,呈正态分布;堆货荷载SQ(年最大值)的统计参数k=0.45,δ=0.244,呈极值Ⅰ型分布[19]。 结构可靠度分析一般可采用一次二阶矩方法,但该方法仅适用于概率密度曲线为单峰的情况。本文中,由于钢筋锈蚀率η(t)的概率密度曲线为双峰,不能直接采用一次二阶矩方法求解可靠指标,为此将式(22)表示为: (23) 式中:x为η(t)的实现值。首先令η(t)=x,按式(23)计算可靠指标β(tη(t)=x)。其次,采用一次二阶矩与数值积分相结合的方法按下式计算构件的失效概率: (24) 式中:fη(x)为锈蚀率的概率密度函数(式(18))。 图9 不同暴露条件的时变可靠指标 β(t)Fig.9 Time-variant reliability index β(t) for different exposure conditions 由可靠指标与失效概率之间的关系β(t)=-Φ-1[pf(t)]即可求得构件不同时刻的可靠指标,3种暴露条件下可靠指标随时间的变化如图9所示。由图9可看出,钢筋锈蚀使钢筋混凝土构件的可靠度降低,第50年时甚至降到2.0以下。3种暴露条件下,水位变动区可靠指标的降低最为明显,其次是大气区,浪溅区降低速度最缓慢。需要注意的是,一般认为浪溅区钢筋的锈蚀比大气区和水位变动区严重,从而浪溅区构件的可靠度下降得更快,但本文结果并非如此。这是因为构件钢筋的锈蚀除与环境有关外,还与采取的耐久性措施有关。本文结果是按规范最低耐久性要求计算得到的,说明规范对浪溅区采取的耐久性措施要比大气区和水位变动区高很多。 针对海洋环境混凝土结构钢筋锈蚀过程的特性,分3种情况对钢筋锈蚀率进行了分析;基于试验数据建立了剩余承载力计算模型;通过Monte Carlo模拟对钢筋混凝土梁的时变可靠度进行分析。分析得出如下结论: (1)海洋环境中的钢筋混凝土构件,t时刻的钢筋锈蚀率与钢筋初锈时间和混凝土保护层开始开裂时间有关。钢筋锈蚀率服从正态-正态双峰分布。 (2)钢筋未发生锈蚀的概率和钢筋已经锈蚀但保护层未开裂的概率随暴露时间t的增加而减小,同时混凝土保护层已经开裂的概率随时间t的增加而增大。 (3)钢筋混凝土构件的可靠指标随时间明显降低。 参 考 文 献: [1]MEHTA P K. Durability of concrete-fifty years of progress[C]∥Proc of the 2nd International Conference on Concrete Durability, 1991, 126: 1-32. [2]杨国平, 贡金鑫, 吴锋, 等. 港工典型钢筋混凝土结构性能退化模型及其评估、预测方法的初步探讨[R]. 北京: 中交水运规划设计院有限公司, 2013. (YANG Guo-ping, GONG Jin-xin, WU Feng, et al. Discussion on performance degradation model and evaluation methods of reinforced concrete structures for port engineerings[R]. Beijing: CCCC Water Transportation Planning and Design Institute Co., LTD, 2013. (in Chinese)) [3]袁迎曙, 贾福平, 蔡跃. 锈蚀钢筋的力学性能退化研究[J]. 工业建筑, 2000, 30(1): 43-46. (YUAN Ying-shu, JIA Fu-ping, CAI Yue. Deterioration of mechanical behavior of corroded steel bar[J]. Industrial Construction, 2000, 30(1): 43-46. (in Chinese)) [4]宋嘉文, 詹元, 金慧珍, 等. 锈蚀钢筋力学性能研究[J]. 低温建筑技术, 2011(6): 8-10. (SONG Jia-wen, ZHAN Yuan, JIN Hui-zhen, et al. Research on mechanical properties of corroded steel bar[J]. Low Temperature Architecture Technology, 2011(6): 43-46. (in Chinese)) [5]沈德建, 吴胜兴. 大气环境锈蚀钢筋混凝土梁力学性能试验研究及分析[J]. 土木工程学报, 2009, 42(8): 75-82. (SHEN De-jian, WU Sheng-xing. Experimental study and analysis on the mechanical performance of corroded reinforcement concrete beams in atmospheric environment[J]. China Civil Engineering Journal, 2009, 42(8): 75-82. (in Chinese)) [6]THOMAS M D A, BENTZ E C. Life-365: Computer program for predicting the service life and life-cycle costs of reinforced concrete exposed to chlorides[R]. American Concrete Institute, Committee 365, Service Life Prediction, Detroit, Michigan, 2001. [7]史波. 氯离子环境下基于概率和性能的混凝土结构耐久性研究[D]. 大连: 大连理工大学, 2009. (SHI Bo. Probability and performance based on durability study for reinforced concrete structures in chloride environment [D]. Dalian: Dalian University of Technology, 2009. (in Chinese)) [8]JTJ 302-2006, 港口水工建筑物检测与评估技术规范[S]. (JTJ 302-2006. Technical specification for detection and assessment of harbour and marine structures[S]. (in Chinese)) [9]SAETTA A V, SCOTTA R V, VITALIANI R V. Analysis of chloride diffusion into partially saturated concrete[J]. ACI Materials Journal, 1993, 90(5): 441-451. [10]张建仁, 王华, 彭建新, 等. 多因素腐蚀环境下混凝土结构的初锈时间模型及其可靠度分析[J]. 长沙理工大学学报: 自然科学版, 2012, 9(1): 34-40. (ZHANG Jian-ren, WANG Hua, PENG Jian-xin, et al. Initiation time model and its reliability analysis for concrete structures under multi-corrosive factors[J]. Journal of Changsha University of Science and Technology (Natural Science), 2012, 9(1): 34-40. (in Chinese)) [11]FRANCOIS R, ARLIGUIE G. Effect of microcracking and cracking on the development of corrosion in reinforced concrete members[J]. Magazine of Concrete Research, 1999, 51(2): 143-150. [12]牛荻涛. 混凝土结构耐久性与寿命预测[M]. 北京: 科学出版社, 2003. (NIU Di-tao. Durability and life forecast of reinforced concrete structure[M]. Beijing: Science Press, 2003. (in Chinese)) [13]LIU T, WEYERS R W. Modeling the dynamic corrosion process in chloride contaminated concrete structures[J]. Cement and Concrete Research, 1998, 28(3): 365-379. [14]VU K A T, STEWART M G. Structural reliability of concrete bridges including improved chloride-induced corrosion models[J]. Structural Safety, 2000, 22(4): 313-333. [15]JTJ 275-2000, 海港工程混凝土结构防腐蚀技术规范[S]. (JTJ 275-2000, Corrosion prevention technical specifications for concrete structures of marine harbour engineering[S]. (in Chinese)) [16]CECS 220: 2007, 混凝土结构耐久性评定标准[S]. (CECS 220: 2007, Standard for durability assessment of concrete structures[S]. (in Chinese)) [17]史志华, 胡德炘, 陈基发, 等. 钢筋混凝土结构构件正常使用极限状态可靠度的研究[J]. 建筑科学, 2000, 16(6): 4-11. (SHI Zhi-hua, HU De-xin, CHEN Ji-fa, et al. Research on reliability of serviceability limit states for structural members of reinforced concrete[J]. Building Science, 2000, 16(6): 4-11. (in Chinese)) [18]贡金鑫, 魏巍巍. 工程结构可靠性设计原理[M]. 北京: 机械工业出版社, 2007. (GONG Jin-xin, WEI Wei-wei. Design principle of engineering structure reliability[M]. Beijing: China Machine Press, 2007. (in Chinese)) [19]GB 50158-2010, 港口工程结构可靠性设计统一标准[S]. (GB 50158-2010, Unified standard for reliability design of port engineering structures[S]. (in Chinese))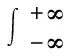


4 抗力衰减模型

5 钢筋混凝土构件的时变可靠度
5.1 功能函数与统计参数
5.2 可靠度分析
6 结 语

