基于球状井非稳定井流理论的管涌流场分布研究

张 健，翟剑峰，王仙美，陈景雅，梁 越

(1. 江苏省交通规划设计院股份有限公司，江苏南京 210005； 2. 江苏省水运工程技术研究中心，江苏南京 211100； 3. 河海大学道路与铁道工程研究所，江苏南京 210098； 4. 重庆交通大学国家内河航道整治工程技术研究中心，水利水运工程教育部重点实验室，重庆 400074)

双层堤基是最常见的堤基形式，尤其在堤防工程以及河堤工程中[1]，这种堤基形式一般由弱透水的上覆层以及强透水的下伏层组成(见图1)。上覆层为自然堆积或人工碾压而成的黏土层，而下伏层为强透水砂层。由于这种特殊的结构形式，使得双层堤基内很容易发生管涌。在双层堤基发生管涌发生前，由于上覆层的渗透性比下伏层小得多，上覆层底面承受很大的水压力，如果压力破坏了上覆层的静力平衡，则水压力会顶穿上覆层形成管涌口。下伏层细颗粒在水流作用下被带出土体，形成集中渗漏通道并引发渗透破坏。室内试验[2-7]、数值模拟[8-10]以及理论分析[11-12]等都是双层堤基管涌发生发展研究的常用方法，而理论分析是研究管涌机理与发展规律的基础。

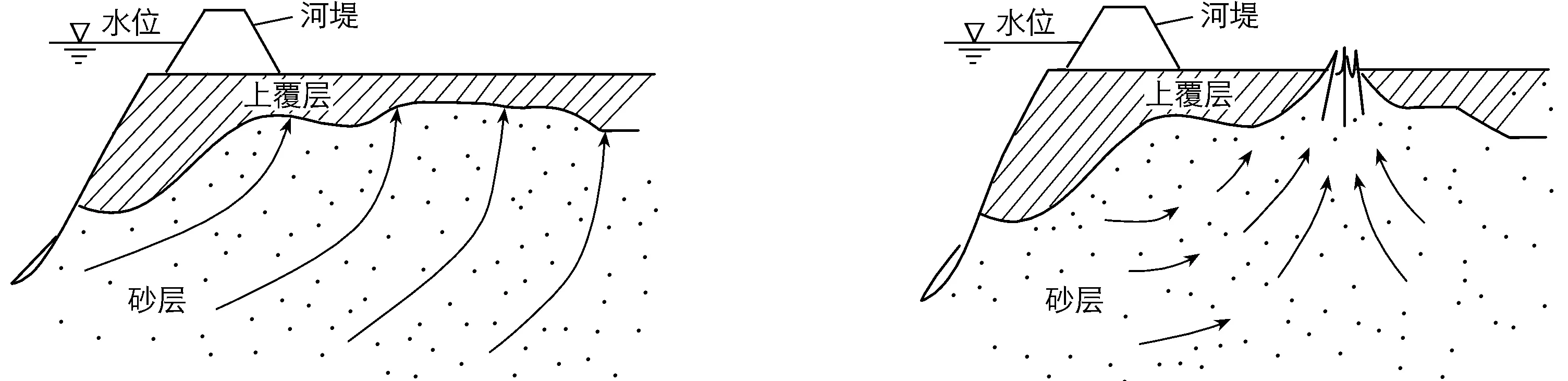
图1 双层堤基管涌前后的流场变化Fig.1 Flow field changes of double-stratum dike foundation before and after piping

管涌的发生发展是渗流场重分布的动态过程，为了分析管涌过程中流场的分布规律，结合管涌的特点，研究人员将井流理论以及镜像井方法引入到管涌问题的分析中。如陈建生等[11]将管涌口等效为虚拟完整井或非完整井，利用虚拟镜像虚拟注水井的方法确定出管涌发生时地层渗流场的分布情况。井流理论与镜像井方法使得管涌时流场的确定有了理论的方法，为管涌时渗流场的确定提供了便利，然而，相关研究还存在两方面的问题。首先，管涌口的形成与管涌的发展是非稳定渗流问题。在管涌口形成前，由于上覆层的弱透水性，上下游的水头差主要由上覆层承担；上覆层破坏形成管涌口后，水头差突然转由下伏砂层承担，其中的高水头来不及消散，管涌口附近势必产生较大的水力梯度，这就会在管涌口形成时产生水砂突然涌出的现象，这一现象在试验中也得到了证实[4]。而现有研究在引入井流理论时，只考虑了稳定井流情况而没有考虑管涌口形成过程中流场变化的动态过程，因此不能很好地描述管涌口形成时流场分布情况。其次，在引入井流理论时，为了简化分析与计算过程，一般将管涌口概化为完整井或非完整井，即管涌口形成时的管涌范围基本贯穿下伏砂层；然而，研究[2，7]表明，双层堤基管涌的破坏范围局限在上覆层与下伏砂层的接触面上，而在深度方向上的发展并不明显。因此，将管涌口概化成完整井或非完整井虽然可以将三维渗流问题转化为二维问题，但与实际情况的差异较大，在工程应用中势必产生较大的误差。

为了更加真实地反应管涌发生发展的工程实际，克服现有研究存在的问题，本文将双层堤基中的管涌口概化为半球状井，并考虑流场分布的动态变化过程，利用非稳态渗流方程对管涌口形成过程中流场的重分布进行推导，分析上覆层破坏、管涌口形成后下伏砂层内的流场分布随时间的变化情况，并根据得到的流场分布对管涌口形成后管涌范围的发展规律进行研究与分析。

1 流场分布的推导

利用非稳态的地下水渗流连续性方程对渗流分布进行推导，各向同性均质地层非稳定渗流的连续性方程[13]为：

(1)

式中：H为水头；μs为贮水率；k为渗透系数。

本文将管涌口概化为半球状，首先推导球状井条件下的非稳态渗流，在球坐标系下对模型进行推导。以管涌口的中心为坐标原点，将式(1)转化为球坐标形式，考虑均质地层情况，并鉴于对称性，上式转化为：

(2)

在双层堤基中，由于上覆层的弱透水性，在上覆层破坏形成管涌口前，绝大部分的水头差都损失在上覆层中，而强透水的下伏层中损失的水头差相对较小，因此，当管涌口形成后，下伏层中的水头要重新分布，这种重分布需要一个过程，因此在管涌口形成的瞬间，下伏层中的水头依然与上游水头相同，即为本文模型的初始条件。假定上游水头在无限远处，且水头高度为H0，结合控制方程与定解条件，球状井在无限空间内非稳态渗流模型如下式：

(3)

式中：rw为管涌口的半径；H1为管涌口处的出水水头；H0为无限远处的外边界定水头。

利用坐标转换以及分离变量法可以得到模型的解为：

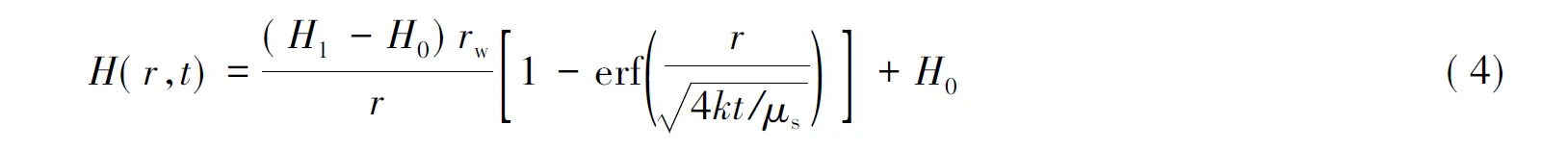
式(4)即为无限空间球坐标系下定水头边界初边值问题的解析解，其中erf为误差函数，表达式为：

(5)

从式(4)中看出，流场中任一点水头的大小仅与其距管涌口的距离有关。对于半无限空间的土体而言，由于对称性，在求解范围内的水头表达式依然是式(4)，则半无限空间内任一点在任一时刻的水位降深为：

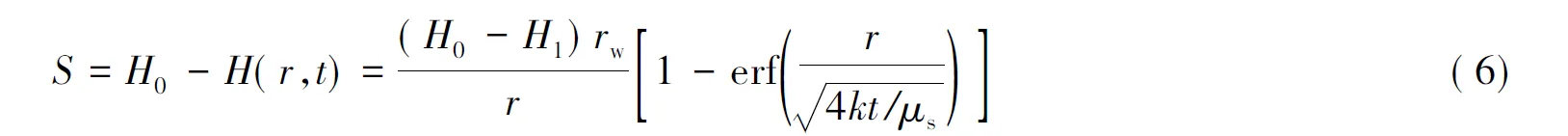
通过式(5)和(6)可以看出，任一时刻半无限空间内水头或降深仅与距离管涌口的距离有关。根据式(4)以及误差的性质可得在半无限空间内半球状井的涌水量为：

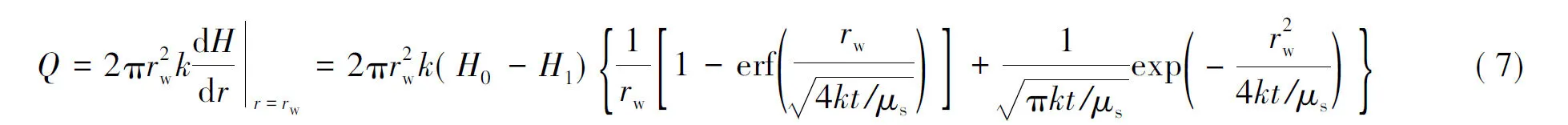
通过上式可以看出，当t→0时，Q→0，即管涌口形成时，水还没有来得及流出；而t→∞，即稳定状态时，流量为：

(8)

2 管涌发生时流场分布的分析

式(4)与(5)所示水头分布与降深为半无限空间内的分布值，在实际的双层堤基中，针对其定水头边界的性质，利用镜像井流理论与叠加原理对双层堤基内的流场分布进行研究。图2为双层堤基管涌口形成后平面流场分布，左侧的河流为线状定水头补给边界，而底部为线状隔水边界。根据镜像井流理论，对于定水头边界，镜像虚拟井与被镜像井的流量相反，但其他性质相同；而隔水边界，镜像虚拟井与被镜像井的流量和其他性质都相同。因此，图2所描述的双层堤基管涌口形成后的渗流问题，可以用图3所示的镜像井模型进行简化。这样，双层堤基中的一个涌水井问题，就转换为1个真实井与3个虚拟井同时工作的干扰井渗流问题。4个井中，2个为抽水井，2个为注水井。抽水井与注水井在任一时刻的水位降深绝对值相等，方向相反。

图2 管涌口附近流场分布 图3 利用镜像法得到的镜像井 Fig.2 Flow field distribution near piping mouth Fig.3 Mirror image wells by using image method

在图3中，4个井分别被命名为井1～井4，并将坐标原点设于图中的O点，x轴与隔水边界相平行，y轴与水头边界平行，而z轴垂直于平面。设管涌口距离上游定水头直线边界的距离为L，下伏砂层的厚度为T。那么在此坐标系下，1个真实井和3个镜像井，即井1～井4中心的坐标分别为(L，T，0)，(-L，T，0)，(L，-T，0)和(-L，-T，0)。根据线性微分方程的性质，图3所示的井流问题可以利用叠加原理进行求解。根据叠加原理，坐标系中任一点的降深即为4个井单独作用时水头降深的叠加(抽水为正、注水为负)，如下式所示：

(9)

式中：S1～S4分别为4个井单独作用时的水位降深，如：

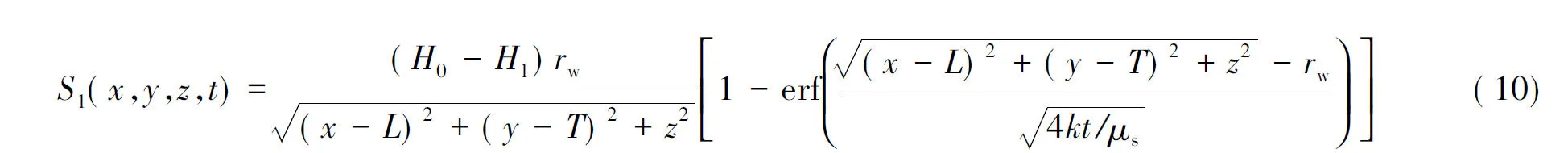
S2，S3和S4具有类似的形式。

根据式(9)，地层中任一点的水头高度为：

(11)

地层中的水力梯度在x方向上的分量为：

(12)

(13)

3 算例分析

如果令初始水头H0=15 m，管涌口形成后的水头H1=5 m，管涌口中心距定水头边界的垂直距离L=100 m，管涌口半径rw=0.4 m，下伏砂层的厚度T=10 m，渗透系数取10-4m/s，砂性土的贮水率可取10-4/m，将这些参数代入式(11)中，即得到渗流场内的水头分布。利用图3所示的坐标系，不同时刻管涌口中心至上游边界垂线以及管涌口中心至底面边界垂线5 m内的水头分布如图4。在初始时刻，地层内的水头值保持恒定，而一旦管涌口形成，水头开始重新分布，且在不同时刻，距离管涌口不同距离处的水头分布具有明显的区别。当管涌口刚刚形成时，管涌口周围土体最先开始出现水头下降，而远离管涌口位置的水头基本还保持原始水头；随着时间的推移，水头下降范围以管涌口为中心向周围传播扩大，且随着时间的增长水头变化的速度逐渐减慢，并向稳定状态发展。

(a) 管涌口至上游边界 (b) 管涌口至底面边界图4 不同时刻管涌口至上游边界和底面边界垂线上的水头分布Fig.4 Water head distribution from piping mouth to the upstream boundary and bottom boundary at different times

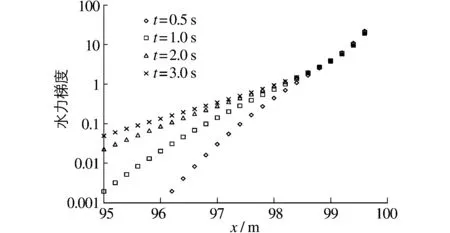
图5 管涌口附近水力梯度随时间的变化Fig.5 Hydraulic gradient change near piping mouth with time

从图4可见管涌口附近的水头变化幅度最大，因此管涌口附近的水力梯度同样有较大值。将各参数代入式(13)中，得到管涌口至定水头边界垂线5 m内的水力梯度分布如图5。在地层的不同位置处，越接近管涌口水力梯度越大，在距离管涌口0.2 m位置处水力梯度达到20以上。在不同时刻，由于水头分布的变化，水力梯度也呈现不同的分布。管涌口形成时，在接近管涌口边缘的位置有非常大的水力梯度，理论上，由于管涌口内边缘上具有水头差但渗径长度为0，这时在管涌口边缘的水力梯度为无限大。随着时间的推移，管涌口边缘处的水力梯度有减小的趋势，而较远离管涌口的水力梯度开始增加。当水头稳定后，水力梯度的分布依然是越靠近管涌口，水力梯度值越大。

4 讨 论

如上所述，管涌的发生是一个由稳态渗流向非稳态渗流转变的动态过程。在管涌口形成以前，上下游的水头差主要由弱透水的上覆层承担，管涌口一旦形成，原本由上覆层承担的水头差转由下伏砂层承担，这种转变使得管涌口周围的水力梯度非常高，因而从下伏砂层突涌出来。毛昶熙等[12]通过试验发现，在管涌口形成时，“流砂喷出孔口，形成高出地面的环状砂丘”；丁留谦等[14]在试验中也发现管涌口形成后“浑水、砂随之涌出孔口，孔内产生砂沸，砂粒随水流带出孔口形成砂环，随着时间的延长，孔口砂沸渐缓，带出孔口的砂粒也渐渐减少”。图6为算例中管涌口形成以后距管涌口中心0.5 m处的水力梯度随时间变化曲线。可见，管涌发生后，管涌口周围水力梯度由接近0迅速增加到20以上，而后逐渐降低并趋于稳定。在管涌形成时，管涌口位置的水力梯度最高，高水力梯度是造成渗透破坏的重要原因；但同时也可看出，在管涌发生时，管涌口周围水头动态变化造成的比稳定状态时更高的水力梯度对管涌的发生与发展同样产生了巨大作用。

上述算例条件下，将管涌口分别等效为球状井以及完整井时稳定井流的水头分布以及水力梯度分布对比见图7。可见，2种条件下水头分布以及水力梯度的分布都有明显区别。对于球状井，其水头分布在由上游水头边界至下游管涌口呈先缓变再急变的趋势。在管涌口水头下降剧烈，而远离管涌口处的水头下降很小；虽然完整井条件下的水头分布也呈现先缓后急的趋势，但在远离管涌口位置处的水位降深要明显大于球状井，且水力梯度沿程的变化幅度较球状井要小。水头分布的差别造成了2种情况下水力梯度分布的差别，水头单位距离内水头变化幅度越大则水力梯度越大，反之水力梯度则越小。从图7中可以看出，在管涌口附近区域两种情况下的水力梯度值都非常高，而球状条件下的水力梯度要高于完整井；而随着与管涌口距离的增加，球状井与完整井条件下的水力梯度值都在下降，但完整井下降的速度要比球状井小，从而在约3倍管涌半径位置处，球状井条件下的水力梯度低于完整井，且越远离管涌口，两者间的差值越大。

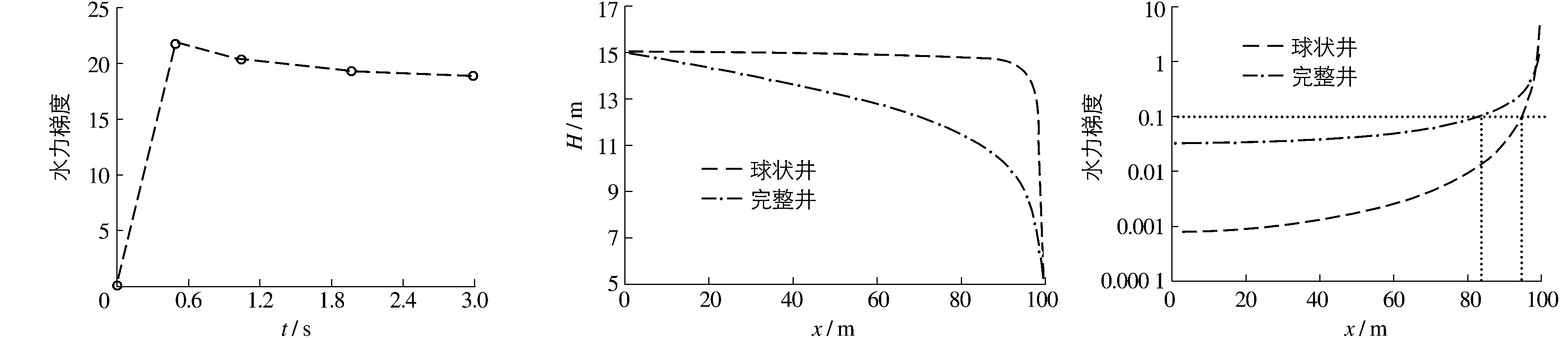
(a) 水头分布 (b) 水力梯度分布图6 管涌口附近0.5 m处水力梯度随时间变化 图7 稳定状态下不同涌水井下水头分布和水力梯度对比Fig.6 Hydraulic gradient change at 0.5 m away from piping mouth with time Fig.7 Water head and hydraulic gradient distribution under different piping wells

管涌口形成以后，在水力梯度作用下，管涌不断向上游发展。水力梯度是管涌发生发展的驱动力，管涌的范围由水力梯度决定，因此，在实际工程中，准确地获取地层中水力梯度的分布是进行管涌预防与抢救的关键。而由图7可以看出，虽然完整井条件下得到的水力梯度在管涌口附近的水力梯度值要比本文的小，但在约3倍于管涌口的距离以外的地方，水力梯度明显大于球状井的计算结果。如取土体管涌的临界水力梯度Jc=0.1，在球状井条件下，管涌口至距其约4 m以内的土层会发生管涌；而在完整井条件下进行判断时，范围扩大到约15 m，两者相差约11 m，因此，管涌口等效为完整井条件下的结果在利用水力梯度对管涌的范围进行判别时，由于高水力梯度的范围明显偏大，使得判别的管涌范围也会偏大。不仅如此，在上文分析中已经说明，管涌口形成以及管涌发展是一个动态过程。管涌口形成后在管涌口附近就产生了非常大的水力梯度，且管涌口形成到渗流场达到稳定尚需要一个时间过程，因此在渗流场未达到稳定以前管涌就已经在不断地发展，因此，利用稳定条件下的完整井流对管涌范围进行判别势必产生较大的误差。

5 结 语

根据双层堤基管涌的特点，将管涌口概化为半球状井，并针对管涌口形成后地层中渗流场重分布问题，利用非稳定井流理论以及叠加原理推导了管涌口形成后地层渗流场的分布模型，并得到了模型的解析解，结合算例，分析了管涌口形成后非稳定井流条件下渗流场的分布规律，得出以下主要结论：

(1)管涌口形成后，管涌口附近土体承担高水头差，因此管涌口附近土体最先出现水头下降，随时间的增长，水头下降区域逐渐向远离管涌口的区域发展。管涌口形成时由于周围土体内高水头未来得及消散，因此管涌口附近土体内将会产生非常高的水力梯度，这是造成管涌口形成后短时间土体突涌而出的原因。

(2)与完整井条件下的渗流场分布相比，球状井条件下土体内水头要高于完整井。在远离管涌口位置，完整井条件下水头变化幅度大于球状井。水头分布的不同导致两种条件下水力梯度的分布也有明显区别，在管涌口附近球状井条件下的水力梯度要高于完整井，但随着与管涌口距离的增加，球状井条件下水力梯度的下降速度要更快，使得完整井条件下的水力梯度更高，因此，在利用两种条件下的水力梯度判别管涌范围时，利用完整井结果判别得到的管涌范围要比球状井的大。

在得到了管涌口形成初始渗流场后，结合管涌发展的特点，可以对管涌的进一步发展进行相关分析。但需要指出的是，管涌的发生发展是一个复杂过程，本文仅针对管涌口形成后渗流场的分布规律提出了一种更符合实际的求解方法。在管涌问题研究中，管涌口形成的机理、管涌的判别条件以及管涌过程中流固耦合规律等都是管涌研究面临的重大问题，这些问题不是独立存在，而是相互联系，因此亟待进行系统地研究。

参 考 文 献：

[1]刘杰. 土的渗透稳定与渗流控制[M]. 北京： 水利电力出版社， 1992： 204. (LIU Jie. The seepage stability and control of the soil[M]. Beijing： China WaterPower Press， 1992： 204. (in Chinese))

[2]梁越， 陈建生， 陈亮， 等. 双层堤基管涌发生发展的试验模拟与分析[J]. 岩土工程学报， 2011， 33(4)： 624-629. (LIANG Yue， CHEN Jian-shen， CHEN Liang， et al. Laboratory tests and analysis on piping in two-stratum dike foundation[J]. Chinese Journal of Geotechnical Engineering， 2011， 33(4)： 624-629. (in Chinese))

[3]毛昶熙， 段祥宝， 蔡金傍， 等. 洪峰过程非稳定渗流管涌试验研究与理论分析[J]. 水利学报， 2005(9)： 1105-1114. (MAO Chang-xi， DUAN Xiang-bao， CAI Jin-bang， et al. Piping experimental study and theoretical analysis of unsteady seepage flow during flood peak[J]. Journal of Hydraulic Engineering， 2005(9)： 1105-1114. (in Chinese))

[4]毛昶熙， 段祥宝， 蔡金傍， 等. 堤基渗流无害管涌试验研究[J]. 水利学报， 2004， 35(11)： 46-53. (MAO Chang-xi， DUAN Xiang-bao， CAI Jin-bang， et al. Experimental study on harmless seepage piping in levee foundation[J]. Journal of Hydraulic Engineering， 2004， 35(11)： 46-53. (in Chinese))

[5]毛昶熙， 段祥宝， 蔡金傍， 等. 悬挂式防渗墙控制管涌发展的试验研究[J]. 水利学报， 2005， 36(1)： 42-50. (MAO Chang-xi， DUAN Xiang-bao， CAI Jin-bang， et al. Experimental study on piping development control by means of suspended cut-off wall[J]. Journal of Hydraulic Engineering， 2005， 36(1)： 42-50. (in Chinese))

[6]倪小东， 王媛， 王飞. 管涌的砂槽试验研究及颗粒流模拟[J]. 四川大学学报： 工程科学版， 2009(6)： 51-57. (NI Xiao-dong， WANG Yuan， WANG Fei. A study of piping by sand-bank model and simulation by PFC 3D[J]. Journal of Sichuan University(Engineering Science Edition)， 2009(6)： 51-57. (in Chinese))

[7]姚秋玲， 丁留谦， 孙东亚， 等. 单层和双层堤基管涌砂槽模型试验研究[J]. 水利水电技术， 2007， 38(2)： 13-18. (YAO Qiu-ling， DING Liu-qian， SUN Dong-ya， et al. Experimental studies on piping in single and two-stratum dike foundations[J]. Water Resources and Hydropower Engineering， 2007， 38(2)： 13-18. (in Chinese))

[8]梁越， 陈亮， 陈建生. 考虑流固耦合作用的管涌发展数学模型研究[J]. 岩土工程学报， 2011， 33(8)： 1265-1270. (LIANG Yue， CHEN Liang， CHEN Jian-shen. Mathematical model for piping development considering fluid-solid interaction[J]. Chinese Journal of Geotechnical Engineering， 2011， 33(8)： 1265-1270. (in Chinese))

[9]周健， 周凯敏， 姚志雄， 等. 砂土管涌-滤层防治的离散元数值模拟[J]. 水利学报， 2010， 41(1)： 17-24. (ZHOU Jian， ZHOU Kai-min， YAO Zhi-xiong， et al. Numerical simulation of piping-filter prevention in sandy soil by discrete element method[J]. Journal of Hydraulic Engineering， 2010， 41(1)： 17-24. (in Chinese))

[10]周晓杰， 介玉新， 李广信. 基于渗流和管流耦合的管涌数值模拟[J]. 岩土力学， 2009(10)： 3154-3158. (ZHOU Xiao-jie， JIE Yu-xin， LI Guang-xin. Numerical simulation of piping based on coupling seepage and pipe flow[J]. Rock and Soil Mechanics， 2009(10)： 3154-3158. (in Chinese))

[11]陈建生， 李兴文， 赵维炳. 堤防管涌产生集中渗漏通道机理与探测方法研究[J]. 水利学报， 2000， 31(9)： 48-54. (CHEN Jian-sheng， LI Xing-wen， ZHAO Wei-bing. Numerical simulation of piping-filter prevention in sandy soil by discrete element method[J]. Journal of Hydraulic Engineering， 2000， 31(9)： 48-54. (in Chinese))

[12]毛昶熙， 段祥宝， 蔡金傍， 等. 堤基渗流管涌发展的理论分析[J]. 水利学报， 2004， 35(12)： 46-50. (MAO Chang-xi， DUAN Xiang-bao， CAI Jin-bang， et al. Theoretical analysis of piping development of levee foundation[J]. Journal of Hydraulic Engineering， 2004， 35(12)： 46-50. (in Chinese))

[13]薛禹群， 吴吉春. 地下水动力学[M]. 北京： 地质出版社， 2010. (XUE Yu-qun， WU Ji-chun. Groundwater dynamics[M]. Beijing： Geological Publishing House， 2010. (in Chinese))

[14]丁留谦， 姚秋玲， 孙东亚， 等. 三层堤基管涌砂槽模型试验研究[J]. 水利水电技术， 2007， 38(2)： 19-22. (DING Liu-qian， YAO Qiu-ling， SUN Dong-ya， et al. Experimental studies on piping development in three-stratum dike foundations[J]. Water Resources and Hydropower Engineering， 2007， 38(2)： 19-22. (in Chinese))