轮图与舵轮图的超边优美标号
,
(1.石家庄邮电职业技术学院 基础部,河北 石家庄 050021;2.石家庄铁道大学 数理系,河北 石家庄 050043)
0 引言
1967年Rosa引入了β-值作为研究完全图分解为同构子图的工具,这就是现在称之为优美标号的雏形。图标号问题主要来源于实际问题,如今其研究成果广泛应用于交换网络理论、X-射线结晶学、射电天文学、雷达和循环设计等领域。
1985年,S. P. Lo[1]首次提出边优美图的概念, 并给出边优美图的必要条件。 关于图的边优美性,Lee[2]提出了一个猜想:所有奇数阶的树都是边优美的。有关图的边优美性更多可参考文献[3-4]。
1994年, Mitchem和Simoson[5]给出了超边优美图的定义。文献[3]中Lee等人证明了K(1,n)当且仅当n是偶数时是超边优美的,双星图DS(m,n)当且仅当m,n都是奇数时是超边优美的,同时他们还猜想:所有奇数阶的树都是超边优美的。文献[6]给出了一些三正则图是超边优美的。目前,超边优美标号的研究还处于起步阶段,研究成果非常有限。
在标号图的讨论中,轮图和舵轮图研究较多。 1978年,C. Hoede和H. Kuiper[7]证明了所有的轮图Wn都是边优美图。1993年,文献[8]给出了轮图Wn优美标号的性质。1989年,文献[9]证明了舵轮图的优美性。本文讨论了轮图Wn与舵轮图Hn超边优美性,证明了这两类图是超边优美的。
1 预备知识
定义1超边优美图
令
称(p,q)-图G是超边优美图,如果存在一个双射f:E→Q,使得它的导出映射
也是一个双射,则f称为图G的超边优美标号,集合P和Q相应称为图G的顶点值集和边标号集。
定义2轮图Wn
由n回路Cn的每一个顶点都与同一个不在Cn上的顶点O相连所得到的图,记作Wn。
它有(n+1)个顶点:O;A1,A2,…,An, 同时包含2n条边,其中:
Ai与Ai+1(1≤i≤n)相邻(记An+1=A1),O与Ai(1≤i≤n)相邻。
在该图中,称顶点O为中心,OAi(1≤i≤n)为轮辐。
定义3舵轮图Hn
由n回路Cn的每一个顶点都与同一个不在Cn上的顶点O相连,然后在Cn的每点再增加一条悬边而得到的图,记作Hn。易见,在轮图Cn之边缘的每个点上, 添加一条悬挂边即为舵轮图。
它有(2n+1)个顶点:O;A1,A2,…,An;B1,B2,…,Bn,同时包含3n条边,其中:
Ai与Ai+1,Bi(1≤i≤n)相邻(记An+1=A1),O与Ai(1≤i≤n)相邻。
在该图中,称顶点O为中心,OAi,AiBi(1≤i≤n)为轮辐。
令a,m是整数,m>0,方便起见,采用记号:
[a,a+m]={a,a+1,a+2,…,a+m-1,a+m};
[a,a+2m]2={a,a+2,a+4,…,a+2m-2,a+2m}。
2 轮图Wn的超边优美标号的构造
轮图Wn,包含(n+1)个顶点和2n条边。 易见, 顶点数的奇偶性由n的奇偶性确定,边数为偶数,故定义中的
Q={-n,-(n-1),…,-1,1,…,n-1,n}。
因为n的奇偶性不同,本文分两种情况讨论:
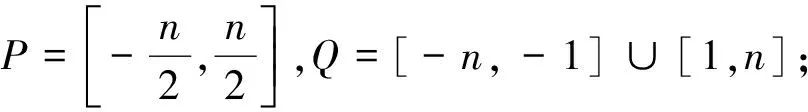

我们的任务是定义一个双射f:E(Wn)→Q,使得它的导出映射
也是一个双射。
定理1当n是正整数时,图Wn是超边优美图。
证明:令
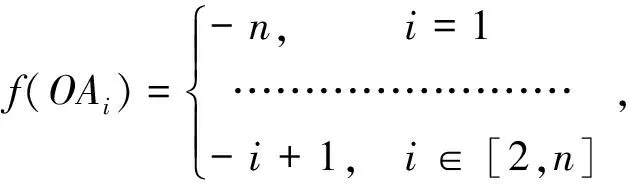

i∈[1,n],f(OAi)的f-值恰充满集合[-n,-1];f(AiAi+1)的f-值恰充满集合[1,n]。所有边的f-值恰充满集合Q=[-n,-1]∪[1,n],故f:E(Wn)→Q是一个双射。下面只需证明导出的各点的f+-值是V(Wn)→P的一个双射即可。
情况1当n≡1(mod 2)时
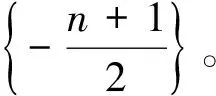

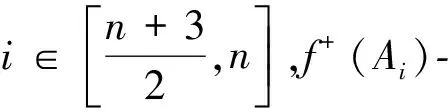
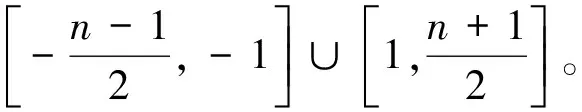
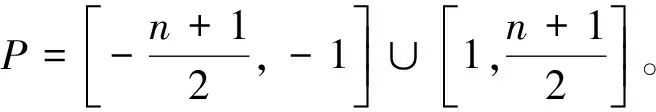
故当n≡0(mod 2)时,f+:V(Wn)→P是一个双射。
情况2当n≡0(mod 2)时
f+(O)=0,
对于点O,其f+-值充满集合{0}。
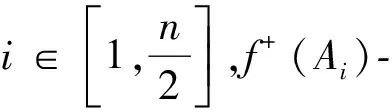
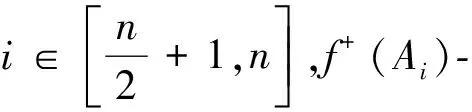



3 舵轮图Hn的超边优美标号的构造
舵轮图Hn,包含(2n+1)个顶点和3n条边。 易见,顶点数目为奇数,边数的奇偶性由n的奇偶性确定。故定义中的
P={-n,-(n-1),…,-1,0,1,…,n-1,n},
因为n的奇偶性不同,本文分两种情况讨论:

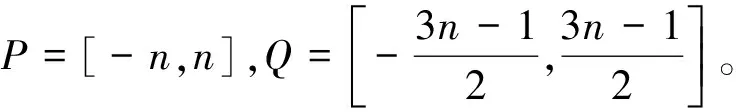
我们的任务是定义一个双射f:E(Hn)→Q,使得它的导出映射
也是一个双射。
定理2当n是正偶数时,图Hn是超边优美图。
证明:令
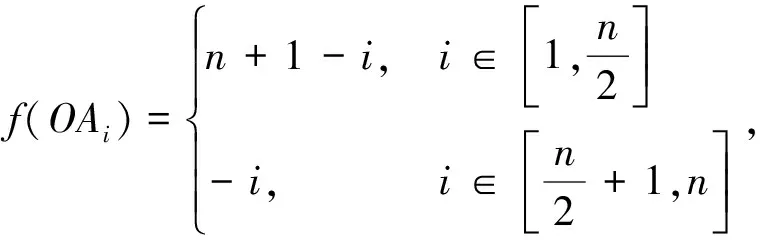
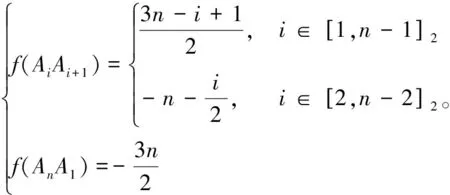









进而,可知导出的各点的f+-值如下:
f+(O)=0,
对于点O,其f+-值充满集合{0}。
i=1,f+(Ai)-值恰充满集合{-n};

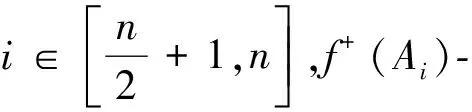
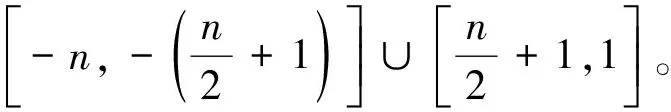

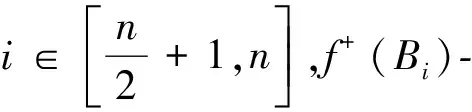

综上,所有点的f+-值恰充满集合P=[-n,n]故f+:V(Hn)→P是一个双射。
故当n是正偶数时,f确是图Hn的一个超边优美双射,故图Hn是超边优美图。
定理3当n是正奇数时,图Hn是超边优美图。
证明:令





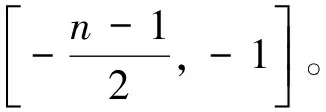

进而,可知导出的各点的f+-值如下:
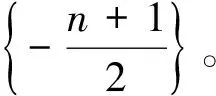


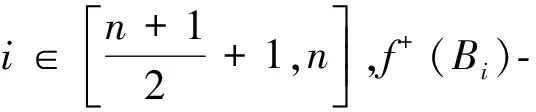
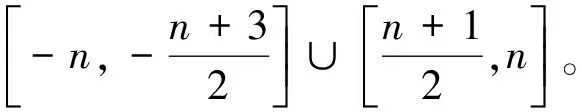
综上,所有点的f+-值恰充满集合P=[-n,n],故f+:V(Hn)→P是一个双射。
故当n是正奇数时,f确是图Hn的一个超边优美双射,故图Hn是超边优美图。
定理4当n是正整数时, 图Hn是超边优美图。
证明:由定理2和定理3知, 该命题成立。
参 考 文 献
[1]Lo S P.On edge-graceful labelings of graphs[J].Congressus Numerantium,1985,50:231-241.
[2]Lee S M.A conjecture on edge-graceful trees[J].Scientia,1989,3:45-47.
[3]Gallian J A.A dynamic survey of graph labeling[J].The Electronic Journal of Combinatorics, 2009,DS6(9): 219.
[5]Mitchem J,Simoson A.On Edge-graceful and Super-Edge-Graceful Graphs[J].Ars Combinatoria,1994,37:97-111.
[6]Shiu W C.Super-edge-graceful labelings of some cubic graphs[J].Acta Mathematica Sinica, 2006,6: 1621-1628.
[7]Hoede C,Kuiper H.All wheels are graceful[J].Utilitas Math,1987,14: 311-316.
[8]黄国泰.关于轮图优美标号的性质[J].数学研究与评论,1993,13(1):40-42.
[9]凌捷.舵图的优美性[J].高校应用数学学报,1989,4(4): 590-592.

