基于SVM的莱州湾叶绿素浓度遥感反演

王春磊，晁 晖，孙 迪

(1.河北联合大学信息工程学院，河北唐山063009;2.北京市第三十五中学，北京100031)

0 引言

叶绿素浓度是海洋中重要的水质参数，其不仅与海洋生态系统初级生产力的研究密切相关，而且对于海洋－大气系统中碳循环、环境监测、赤潮灾害监测等的研究以及渔业管理都具有重要意义。海洋遥感可以实现大面积、实时、同步、连续及密集的海洋探测，弥补了传统方法对个别点、离散区域、不同时间、不同地点观测的不足。因此我们可以通过遥感获取海洋的叶绿素浓度信息，为海洋水体富营养化监测和评价提供新方法。

本文利用莱州湾海域32组2007年6月至9月现场ASD实测的遥感反射率以及对应点的叶绿素浓度，研究其反射光谱特征建立遥感反演叶绿素浓度模型，为估算本海域的叶绿素浓度提供参考。

1 采样数据

其中:RN(λi)是归一化的水体反射率，R(λi)是原始的水体反射率，n是400～880 nm波段之间的波段数。

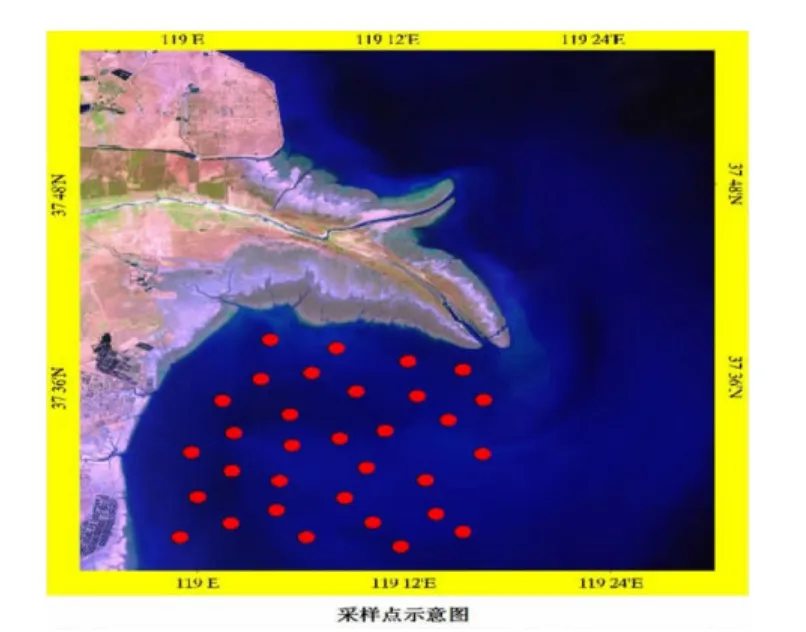
图1 采样点示意图

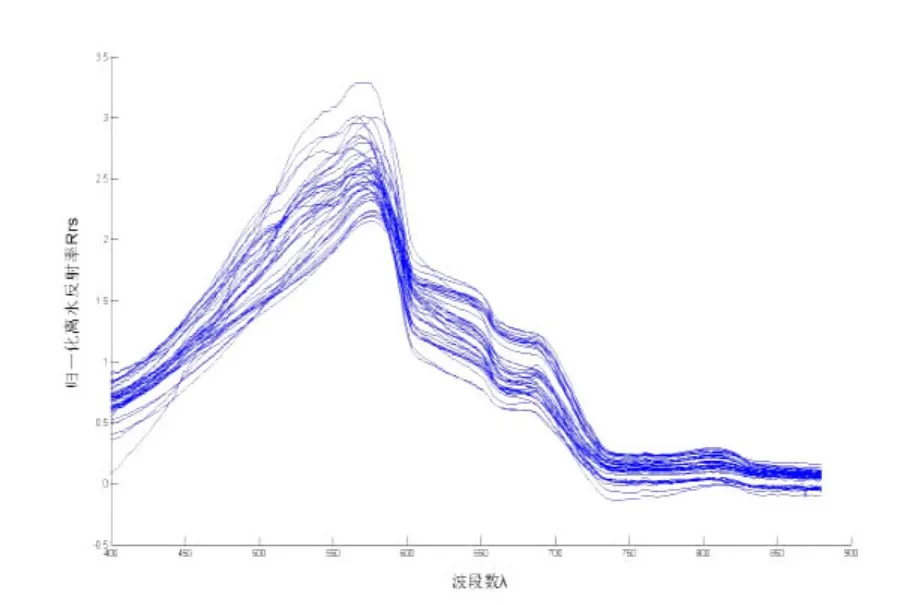
图2 归一化后的实测光谱特征曲线

根据图2可知，原始的水体反射率经过归一化处理之后，曲线变得相对集中，有效地抑制和消除了由于环境因素不同而对光谱曲线造成的整体性抬高或降低;同时，也使光谱曲线的波峰和波谷变得更加明显和突出。波谷出现在660 nm左右，波峰出现在560 nm左右，其中在690 nm附近形成荧光峰。

2 反演模式

2.1 叶绿素荧光算法

浮游植物在400 nm～800 nm太阳光的激发下，在685 nm附近产生荧光效应［1-2］，它是浮游植物光合作用和生理状态最有效的探针之一。叶绿素荧光效应为解决二类水体叶绿素反演提供了很好的研究方向。根据水色组分的光谱特性研究结果，荧光携带了大量叶绿素信息而很少有其他水色信息的干扰，用荧光算法反演叶绿素有较高的反演精度。荧光位于红光波段，受大气气溶胶的影响要比蓝光和绿光波段小很多，大气对荧光的影响较小。因此，通过水体反射率或遥感反射率光谱中提取太阳光激发的叶绿素荧光信号估算表层叶绿素浓度是目前水色遥感研究的热点和新的发展方向［3-4］。

叶绿素荧光峰的位置随着叶绿素浓度的增加向长波方向移动，Gitelson［5］对“红移”现象的研究表明，当叶绿素浓度小于3 mg/m3时，荧光峰的位置大致在683 nm处;当叶绿素浓度增加到10 mg/m3时，荧光峰慢慢移动到685 nm处;而当叶绿素浓度大于100 mg/m3时，荧光峰的位置在688 nm左右;达到300 mg/m3时，荧光峰到达705 nm甚至更远。本次采集的数据叶绿素浓度范围0.68 mg/m3～9.5 mg/m3，荧光峰波段大致在680 nm～700 nm之间，与Giteslon的研究基本一致。目前的荧光法主要有归一化荧光高度法和基线荧光高度法。

归一化荧光高度法的基本原理是通过685nm附近的荧光峰值的辐射率R685除以560 nm附近的反射峰Rmax或675 nm附近吸收谷的辐射率，得到归一化荧光高度(Normalized Fluorescence Height，NFH)，然后建立NFH与叶绿素浓度的关系模型。

基线荧光高度法是使用荧光峰左右两侧通道(λ1、λ3)的离水辐亮度的连线为基线，计算荧光通道(λ2)的离水辐亮度在基线之上的高度，称为基线荧光高度(Fluorescence Line Height，FLH)，公式如下(3)，叶绿素浓度的反演公式为(4):

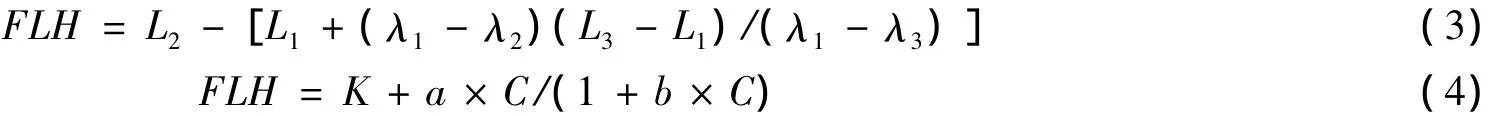
式中:λ2为中心波长;λ1、λ3为选定的基线波长;L1、L2、L3为相应波段对应的辐亮度值。C为海面叶绿素浓度(单位:mg/m3);FLH为荧光基线高度值(单位:mW/(cm2·sr·nm));a，b，k为系数。

左侧的基线波段选择λ1为665 nm，基线右侧λ3的选取为709 nm，这个波段两侧吸收和反射相对稳定，避开了730 nm水汽吸收波段和760 nm氧吸收波段以及更长波段时悬浮泥沙的影响;λ2的选取为逐个点遥感反射率在665～709 nm区间的极值。

tere kümün öɡdör(ööɡedör)tere tuqai ü (那个人昨天就把那件事说了)

结合实测的光谱曲线，采集所有点在560 nm附近的反射峰，以685 nm作为荧光峰进行归一化荧光法研究，建立NFH(560)同叶绿素浓度的相关关系，运用Curveexpert曲线自动优化搜索，结合标准差最优，发现NFH与叶绿素浓度的线性关系最为符合(图3)。通过选定的基线波段和荧光波段，利用基线荧光高度算法计算得到了32个基于实测的遥感反射率射率光谱的荧光峰高度FLH，与对应的叶绿素浓度进行拟合，结果如图4:

图3 NFH线性模型及预测

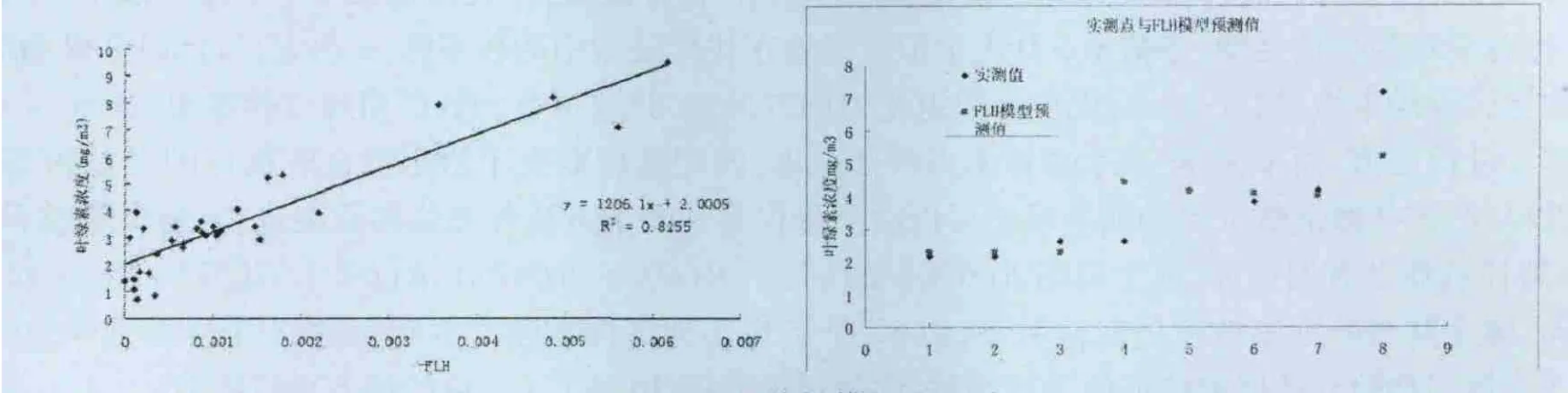
图4 FLH线性模型及预测

2.2 基于特征光谱的SVM算法

支持向量机(SVM)是Vapnik等人提出的新型机器学习方法［6-7］，它建立在统计学习理论的VC维理论和结构风险最小原理基础上，根据有限样本信息在模型的复杂性和学习能力之间寻求最佳折衷，以期获得最好的推广能力［8-9］。由于SVM具有良好的推广特性，目前已成功地应用于函数逼近、信息融合等领域［10］。本文主要采用支持向量机在函数拟合中的应用:

拟合给定数据点集，使函数(6)最小

惩罚函数采用ε—不灵敏损失函数:

函数拟合可以表示为一个最优问题:

其中ε表示逼近精度ξi≧0和≧0为松弛因子，式中的第二项是对超出逼近精度样本的惩罚，常数控制对错分样本惩罚的程度。采用对偶理论，将其转化为二次规划问题:

求解该二次规划问题，可得:

引入高斯核函数

其中σ是尺度函数，它的取值决定拟合函数的支持度和平滑性，σ的选择随散乱数据点分布自适应改变，散乱点集X的分布可以用参数Q(X)描述:

其中Ω是包围散乱点集X的区域。选择σ使Q(X)/σ=常数，这样就能保证每个节点函数局部拟合质量，从而提高全局拟合的性能。参数γ＞0表示拟合误差在代价函数中的权系数。γ越大，拟合误差权重越大，拟合函数越逼近样本点。当γ→∞，代价函数退化为均方误差，此时拟合函数严格经过样本点。即γ→∞ 表示对样本点进行插值，而γ≠∞表示对样本点最佳逼近。因此选择取决于给定散乱数据点的误差和实际需要的逼近程度，这些散乱数据点的测量误差可以由测量仪器和测量方法等先验知识决定。实验步骤如下:

(1)特征选择和数据缩放:本文采用R(678)/R(479)、R(600)/R(479)、R(600)/R(571)、NFH和FLH作为输入，建立其与叶绿素浓度的对应关系，以32个点作为训练样本建立判别函数，8个样本点作为验证。分别对训练数据和验证数据的特征值进行缩放，缩放后的范围为［－1，1］，目标值不进行缩放;

(2)参数选取:首选选择SVM中的核函数进行选择，实验中选用的是使用最为广泛的径向基核函数(RBF)，然后利用交叉验证和网格选参的方法进行支持向量回归机算法中的3个参数进行选优，分别是惩罚参数C，RBF核函数中的参数λ，精度参数ε。实验中通过对不同的C=［2－1，20，21，22，23，24，25，26］，λ =［20，2－1，2－2，2－3，2－4，2－5，2－6，2－7，2－8］，和ε =［2－8，2－7，2－6，2－5，2－4，2－3，2－2，2－1］进行5－折交叉验证的均方误差(MSE)估计，选取使MSE最小的那组参数作为最终建模的最优参数;

③构建模型及结果评价:根据选取的最优参数，训练样本数据，结合支持向量回归机算法进行模型训练，构建回归模型;根据模型训练构建的模型，对验证样本数据进行结果检验，并选择评价指标对验证结果进行评价，实验中选取的评价指标为均方误差(MSE)和相关系数平方(R2)。

参量选取:惩罚参数C 64;核函数－高斯核函数参数0.015625;精度参数0.5。网格选优的最优参数对应的训练精度0.920607;训练样本数32;验证样本8;特征数2;验证结果评价:训练模型评价R2=0.851362;均方误差0.861364;预测R2=0.8307。

表1 荧光模型及SVM拟合误差评价

3 小结

本文建立了莱州湾叶绿素浓度反演的新方法，对32组实测光谱水体反射率归一化后根据叶绿素的荧光特征建立NFH和FLH反演模型，以及结合光谱拐点值的比值模型和荧光模型建立SVM算法，用剩下8条光谱曲线进行模型验证。发现NFH和FLH模型中FLH误差较小，SVM算法则达到最小。肯定了利用叶绿素荧光特性探测叶绿素浓度的有效性，同时说明了SVM采用结构风险最小化准则的特性能有效地对叶绿素光谱特性进行拟合，并在二类水体叶绿素浓度反演、水质监测等方面有良好的应用前景，并为以后利用NFH和FLH组合来反演叶绿素浓度提供参考。

［1］ 朱延彬，吴燕燕.天然叶绿素荧光特性研究［J］.光谱学与光谱分析，1995，15(2):5-8.

［2］ Neville R A，Gower JFR.Passive remote sensing of phytoplankton via chlorophyll-alpha florescence［J］.Journal ofGeophysicalResearch.1977，82 (24):3487-3493.

［3］ Maxwell K.，Johnson G.N.Chlorophyll fluorescence-a practical guide［J］.Journal of Experimental Botany.2000，51:659-668.

［4］ Xing X G，Zhao D Z，etc.An overview of Remote Sensing of Chlorophyll Fluorescence［J］.Ocean Science Journal，2007，Vol.42，No.1:49-59.

［5］ Gitelson AA.Algorithms for Remote Sensing of phytoplankton pigments in land waters［J］.Advanced Space Research，1993，13:197-201.

［6］Vapnik V.The Nature of Statistical Learning Theory［M］.New York:Springer，1995.

［7］Vapnik V.Statistical Learning Theory［M］.New York:Wilcy，1998.

［8］崔伟东，周志华，李星.支持向量机研究［J］.计算机工程与应用.2001，37(1):57-61.

［9］ Snykons JA，etc.Sighted least squares support vectormachines:robustness and sparse approximation［J］.Neurocomputing，2002;48:85-105.

［10］ 阎辉，张学工，李衍达.支持向量机与最小二乘法关系研究［J］.清华大学学报(自然科版).2001，41(9):77-80.