基于迭代法的工业以太网性能分析
刘 程,夏继强
(北京航空航天大学机械工程及自动化学院,北京 100083)
0 引言
共享式以太网采用CSMA/CD访问机制,各节点采用二进制指数退避算法来处理冲突,这导致了以太网通信延迟不确定的缺点,成为以太网在工业实时控制领域应用的最大障碍[1-2]。当今已经提出了很多种改进方法来解决这个问题,比如通过修改以太网协议、在以太网MAC层上增加虚拟令牌等软件实时方法[3];改变以太网拓扑结构[4-5]、进一步细分以太网结构等硬件实时方法[6];或者将信号的频分复用传输应用到以太网[7]。其中交换式以太网的出现极大地提高了以太网传输性能。交换机作为一种能隔绝冲突的二层网络设备,在同一时刻可进行多个端口对之间的数据传输冲突机率大大减小,但多个端口同时尝试与一个端口通信时依然存在冲突的可能,这可看作另外一种形式的抢占信息通道,只是发生概率减小。端口使用缓存能解决此类冲突,但增加了信息传输延时的不确定性。因此在工业控制背景下,定量研究和分析冲突机制,对于以太网技术能够广泛应用到工业控制领域具有重要意义。
文中拟采用一种新方法来研究共享传输介质的传输冲突特性,以工业共享式以太网为对象,首先建立基于CSMA/CD机制的以太网数学模型,然后基于此模型对以太网进行定量计算,考虑负载的变化(如节点数,数据到达率)对以太网性能的影响,从而进一步分析以太网的实时性及可靠性。
1 以太网模型
工业以太网具有周期信号多,传输信息量小,信息长度小,负荷平稳的特点,因此采用以下以太网模型,符号含义如表1:
(1)坚持型CSMA,当某节点要送数据时,先监听总线,若总线忙,就坚持监听,直到信道空闲为止,当空闲时立即发送一帧数据。
(2)节点发生冲突后,按照二进制指数退避算法推迟发送,冲突次数达16次则发送失败[8]。冲突后节点发送加强干扰信号(JAM信号)。
(3)星型网络,节点使用集线器连接,设任意两节点之间的传播延时都等于τ.
(4)由于发生3个及以上节点的冲突概率很小,远远小于两节点的冲突概率,因此只考虑两个节点之间的冲突。

表1 符号说明
2 原始负载模型分析
原始负载模型是指不考虑节点冲突后重传数据帧,每个数据帧不管发送是否成功,只传输一次时的负载模型。
2.1相邻数据帧到达时间间隙
N个节点以数据到达率λ0随机且独立地发送数据,由二项分布的定义可知,单个节点在任意的时隙t(t<<1/λ0)内发送了数据的概率为:
P=λ0t=t/T0
(1)
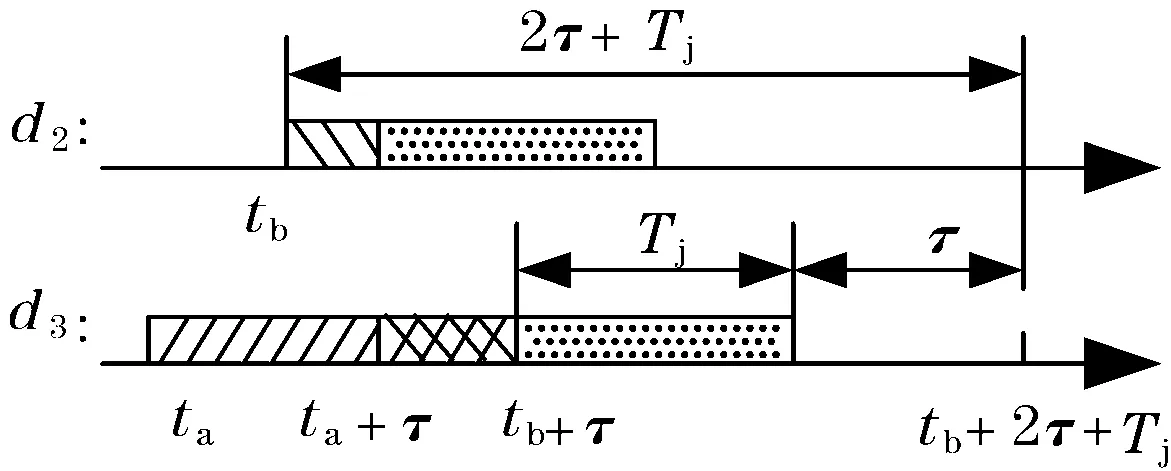
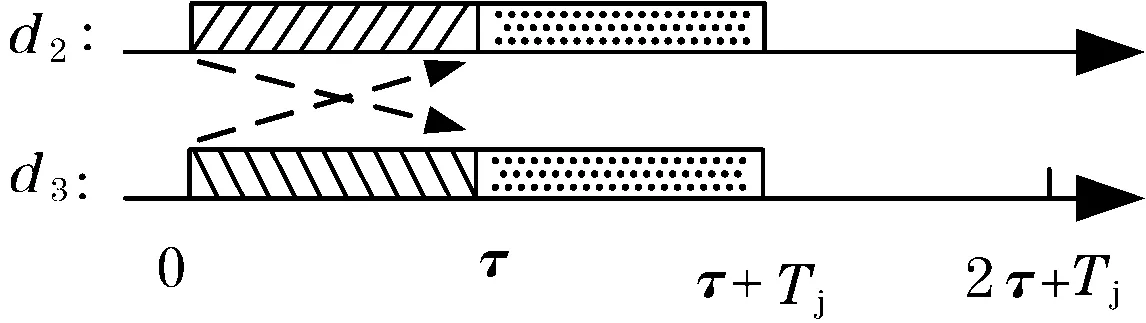
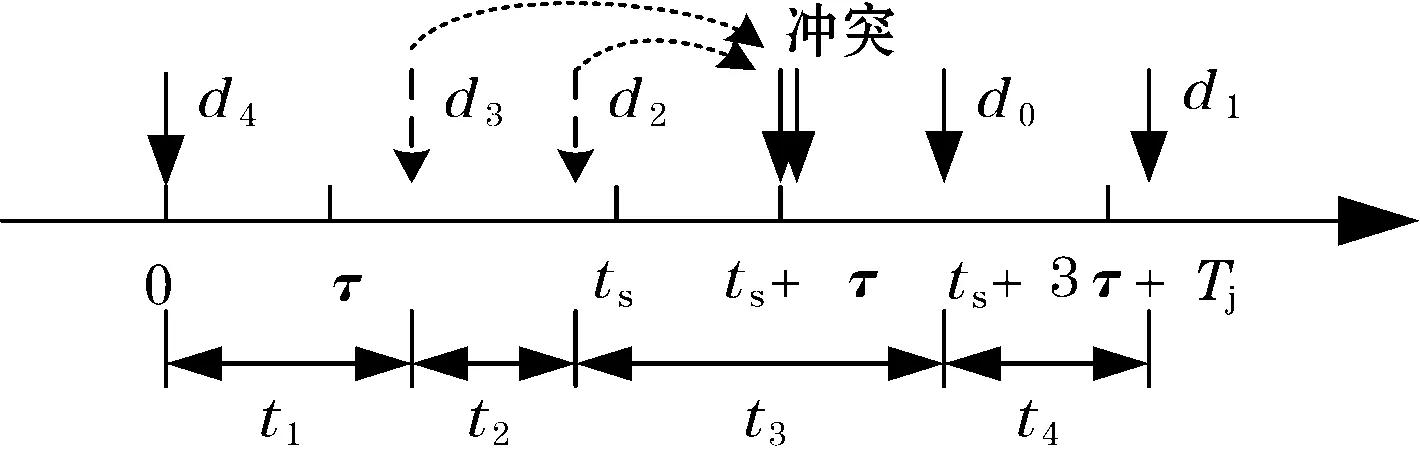
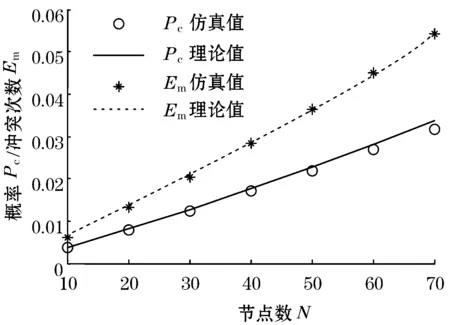
如图1所示,节点d4在0时刻开始发送数据,其后相继到达的节点之间的时间间隔分别用t1、t2、t3、t4表示。在节点d4发送数据后的t时间段内,若有其他节点尝试占用总线(即节点d3落在0~t时间段内),则t1 图1 数据到达模型分析 由二项分布可得: P(t1 (2) (3) (4) (5) 对t1的分布函数式(2)求导可得t1的概率密度函数: Ωt1(t)=λ0×(N-1)(1-p)N-2 (6) 2.2冲突模型分析 任意的数据帧发送时可能发送成功或发生冲突,其中冲突可分为等待冲突和延时冲突。等待冲突是指总线被占用时有多个节点需要发送数据,这些节点在总线变空闲后同时发送数据造成的相互之间的冲突。延时冲突是指一个节点已经开始发送数据,但由于总线传输延迟,其他节点未检测到总线被占用,并且发送数据所造成的冲突。 下面按照d0前一个节点d2的发送结果,分为成功和冲突2种情况,逐步分析d0的发送结果。分别以Ps、Pd、Pw表示发送成功、发生延时冲突和发生等待冲突的概率,可得Ps+Pd+Pw=1。 2.2.1节点d2发送成功 如图2所示,节点d2从0时刻开始发送一帧数据,其成功发送的概率为Ps,由于数据在节点间传输存在时长为τ的延时,其他节点在ts+τ时刻才监听到总线空闲,因此d2占用总线从0时刻到ts+τ时刻。由于前提为d2成功发送,因此d0会在τ时刻之后到达,否则d2、d0发生延时冲突。 图2 d2节点发送成功条件下d0节点的冲突模型 下面分4种情形讨论d0的发送结果。 情形①:若d0、d1两节点都在ts+τ时刻之前到达,即满足t1+t2 Ps×P(t1+t2 (7) 情形②:若节点d1在ts+2τ之后发送数据,则d0、d1是否冲突取决于d0、d1发送数据的时间间隔t2,若t2>τ则节点d0成功发送数据,此情形发生概率为: Ps×P((t1+t2>ts+τ)&(t2>τ))= (8) 式中Ωt2(t)来自式(6)。 情形③:若节点d1在ts+2τ之后发送数据,且t2<τ则d0、d1发生延时冲突,此情形发生概率为: Ps×P((t1+t2>ts+2τ)&(t2<τ)) (9) 情形④:若ts+τ Ps×P(ts+τ (10) 2.2.2节点d2发生冲突 节点d2发生冲突的概率为Pc,冲突对象可以分为节点d3和节点d02种,根据总线上数据帧之间的等效性,两种冲突的概率相等,即Pc/2。 2.2.2.1节点d2与d0冲突 d2与d0发生冲突的概率占d2发生冲突概率的一半,即d0与d2发生等待冲突的概率为: Pw/2 (11) d0与d2发生延时冲突的概率为: Pd/2 (12) 2.2.2.2节点d2与d3发生延时冲突 图3显示了d2、d3的延时冲突模型,两节点分别在ta、tb时刻发送数据,节点d2在ta+τ时刻检测到冲突,随之发送时间长度为Tj的JAM信号。节点d3在tb+τ时刻检测到冲突,并在tb+2τ+Tj时刻结束发送,由于传输延迟,其他节点认为总线一直被占用直到tb+2τ+Tj时刻才结束。因此从节点d2开始发送数据到整个冲突占用总线结束,所经历的时间长度为固定值2τ+Tj. 图3 延时冲突 节点d2、d3发生延时冲突的概率为Pd/2。采用与2.2.1小节相同的分析方法,将d2数据帧占用总线时间由ts+τ变为2τ+Tj.同理可得d2与d3发生延时冲突时,d0发生等待冲突的概率为: (13) d0发送成功的概率为: (14) d0发生延时冲突的概率为: Pd2×P((t1+t2>3τ+Tj)&(t2<τ))+ (15) 2.2.2.3节点d2与d3等待冲突 图4为等待冲突模型,节点d2、d3等待总线空闲后同时向总线发送数据,经过时间τ后被对方检测出冲突,分别发送JAM信号,并且信息传输延迟1倍τ长的时间,即等待冲突占用总线总时长为2τ+Tj。 图4 等待冲突 如图5所示,由于等待节点d4发送结束,节点d2、d3推迟到ts+τ时刻发送数据,并发生等待冲突,冲突占用总线直到ts+3τ+Tj时刻,其发生概率为Pw/2。考虑节点d4成功发送数据,否则总线上连续5个数据帧发生冲突,此情形发生概率很小,文中忽略不计。 图5 d2、d3发生等待冲突模型 此情形的分析方法与小节2.2.1相同,但是数据帧增多,时间增长,同样原理分析可得d2、d3发生等待冲突时,d0发生等待冲突概率为: (16) d0发送成功的概率为: (17) d0发生延时冲突的概率为: (18) 2.3发送冲突的概率Pc 由式(8)、式(14)、式(17)相加可得节点d0成功发送数据的概率Ps,式(7)、式(11)、式(13)、式(16)相加可得节点发送数据发生等待冲突的概率Pw,以及已知成功发送数据和发生冲突的概率和为1,因此可得以下方程组。 Ps=Ps×P((t1+t2>ts+2τ)&(t2>τ))+ (19) Pw=Ps×P(t1+t2 Pw/2+Pw×P(t1+t2<2τ+Tj)/2+ (20) Ps+Pw+Pd=1 (21) 由方程组,通过数值迭代法可解出Pw、Pd,从而计算出数据帧发生冲突的概率值Pc=Pw+Pd. 一个数据帧冲突后再次发送时仍然可能冲突,且冲突分为2种类型,一种为与新的节点冲突(如图6中的分支b×Pc),一种为与前一次冲突节点再次冲突(如图6中的分支a×Tij)。采用同样的方法分析数据帧第2次、第3次直到第15次发送,即可得数据帧冲突次数的模型,如图6所示。 图6 数据帧冲突次数分析 a:连续多次冲突的两节点发生第一次冲突时的概率。 b:前一分支点所对应的概率。图中虚线指明系数a、b所代表的值。 Tij:节点从i-j+1次冲突开始,与同一节点连续冲突j次的概率。其中i表示节点当前总共冲突次数;j表示其连续与同一节点冲突的次数。 Qn:数据帧至少发送n+1次的概率(0≤n≤15),即至少冲突了n次,其中Q0=1。 同样原理分析可以得Tij的计算通式为: (22) 在已知Pc的前提下,可以把图6从左至右所有分支点都求解出来,之后将图6第n列(1≤n≤16)概率相加可得至少冲突n次的概率Qn,即 (23) 再用Qn减去Qn+1即可得数据帧冲突n次(第n+1次发送成功)的概率Kn+1。 Kn+1=Qn-Qn+1 (24) 通过式(22)~式(24),采用迭代法循环计算可得在已知冲突概率Pc时,数据帧发送n次才成功的概率值Kn.多次迭代数值稳定后由数组K可得冲突次数的期望值Em: (25) 由上一章节可知,在已知冲突概率Pc的前提下可以求得数据帧发送时冲突次数的期望值Em.冲突导致了部分数据帧需要多次发送,对此可看作节点需要发送的数据帧增多,数据到达率变大为λ1=λ0+λ0×Em.由于工业以太网负载小,上述所有算式依然近似成立,将新的数据到达率带入式(1)~式(21)求出新的Pc值。如此反复迭代计算,数据值趋于稳定时即在原始到达率λ0的条件下,实际总线上的传输情况。 本节使用Matlab编程模拟以太网协议,节点冲突后按照二进制指数退避重传。图7、图8显示了在λ0=167 帧/s,帧长为64字节,网络带宽为100 Mbit/s,ts=5.12 μs,τ=1.2 μs时Pc、Em以及节点发送5~7次的概率K2~K7随节点数N变化的值。理论值分别由式(19)、式(20)、式(21)、式(24)、式(25)计算。 图7 Pc与Em随N变化的仿真值与理论值对比 图8 K5~K7随N变化的仿真值与理论值对比 图9、图10显示了在节点数N=50时,Pc、Em以及节点发送5~7次的概率K2~K7随数据到达率λ0变化的值。其他参数同上,理论值由式(19)、式(20)、式(21)、式(24)、式(25)计算。 图9 Pc与Em随λ0变化的仿真值与理论值对比 图10 K5~K7随λ0变化的仿真值与理论值对比 本文通过迭代法计算了以太网通信时数据帧冲突的概率以及发送次数的期望值,求解了各个参数对共享式以太网的影响,仿真结果显示了算法的正确性和有效性。下一步可以采用迭代方法计算交换式以太网争夺同一端口通信权的冲突概率,以此分析交换式以太网的性能。 参考文献: [1]CHOI B Y,SONG S,BIRCH N,et al.Probabilistic approach to switched ethernet for real-time control applications.Seventh International Conference on Real-time Computing Systems and Applications,2000:384-388. [2]陈曦,刘俊峰,付少波.工业以太网传输延时特性分析.计算机与信息技术,2007(14):62-66. [3]CUONG D M,KIM M K,LEE H C.Supporting hard real-time communication of periodic messages over switched ethernet.The 1stInternational Forum on Strategic Technology,2006:419-422. [4]朱政红,王月娥.工业以太网在控制领域中的实时性技术.低压电器,2010(7):31-37. [5]杨夏,毕艳冰,孙延涛.交换式以太网物理拓扑发现的进展与研究.计算机用用研究,2007,24(12):24-27. [6]康葆荣.工业以太网实时性问题及解决方案.电脑开发与应用,2006(7):38-40. [7]夏继强,邢春香.现场总线工业控制网络技术.北京:北京航空航天大学出版社,2005:42-49. [8]IEEE Std 802.3.Part 3:Carrier Sense Multiple Access with Collision Detection (CSMA/CD)access method and physical layer Specification.ISO/EEC 8802-3:2000 (E),2000. [9]SCHNEIDER S,PARDO C G,HAMILTON M.Can Ethernet be real time?[EB/OL].Real-Time Innovations,Sunnyvale,CA.http://www.rti.com/products/ndds/ ethernet.pdf. [10]XIA J Q,CAO Q,BAI R G.Modeling and quantitative real-time analysis of Ethernet based on CSMA/CD.the 13th IEEE Joint International Computer Science and Information Technology Conference(JICSIT 2011),accepted.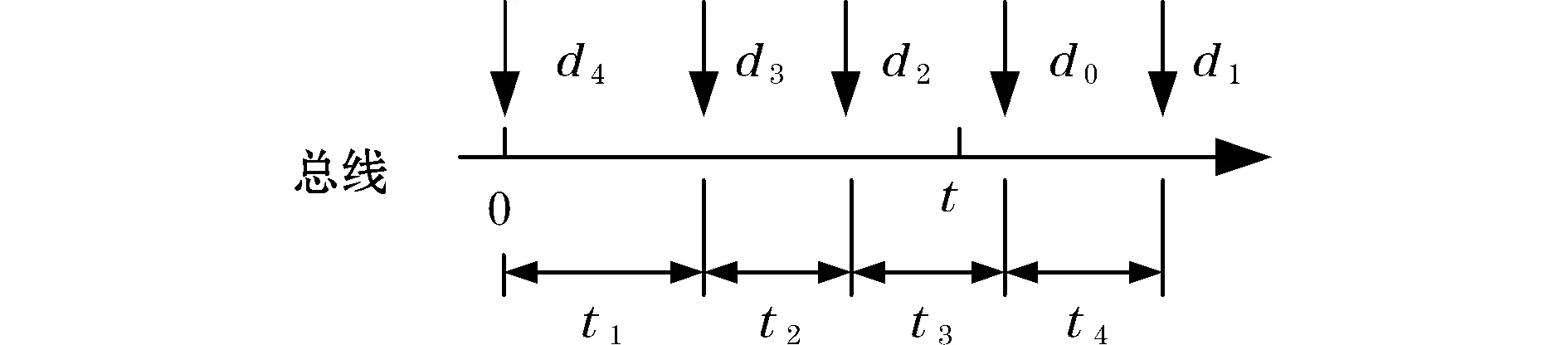


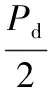
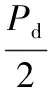

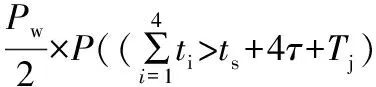
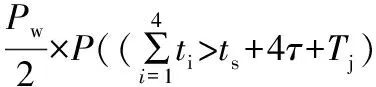

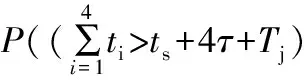
3 冲突次数的期望值Em
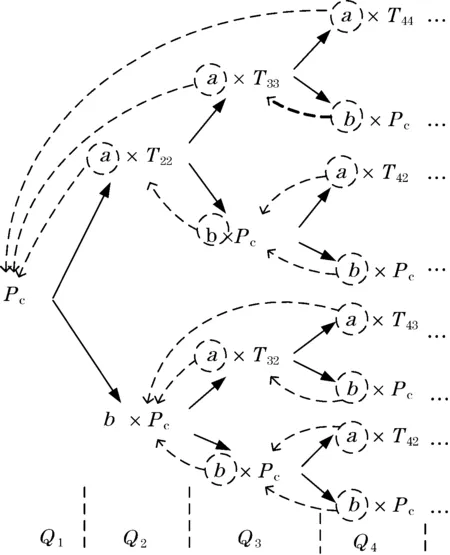
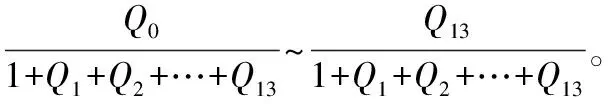
4 迭代求解
5 仿真验证

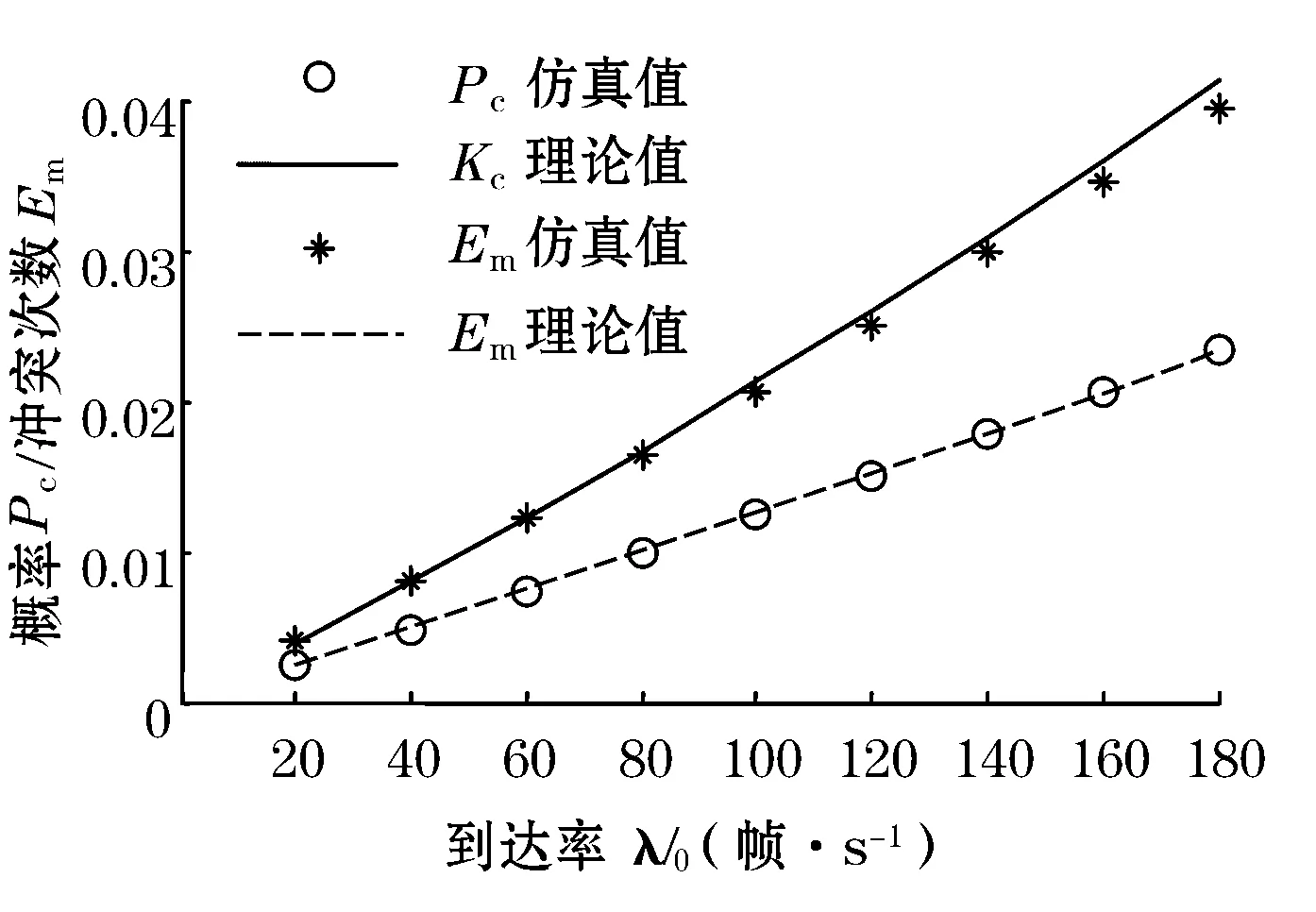
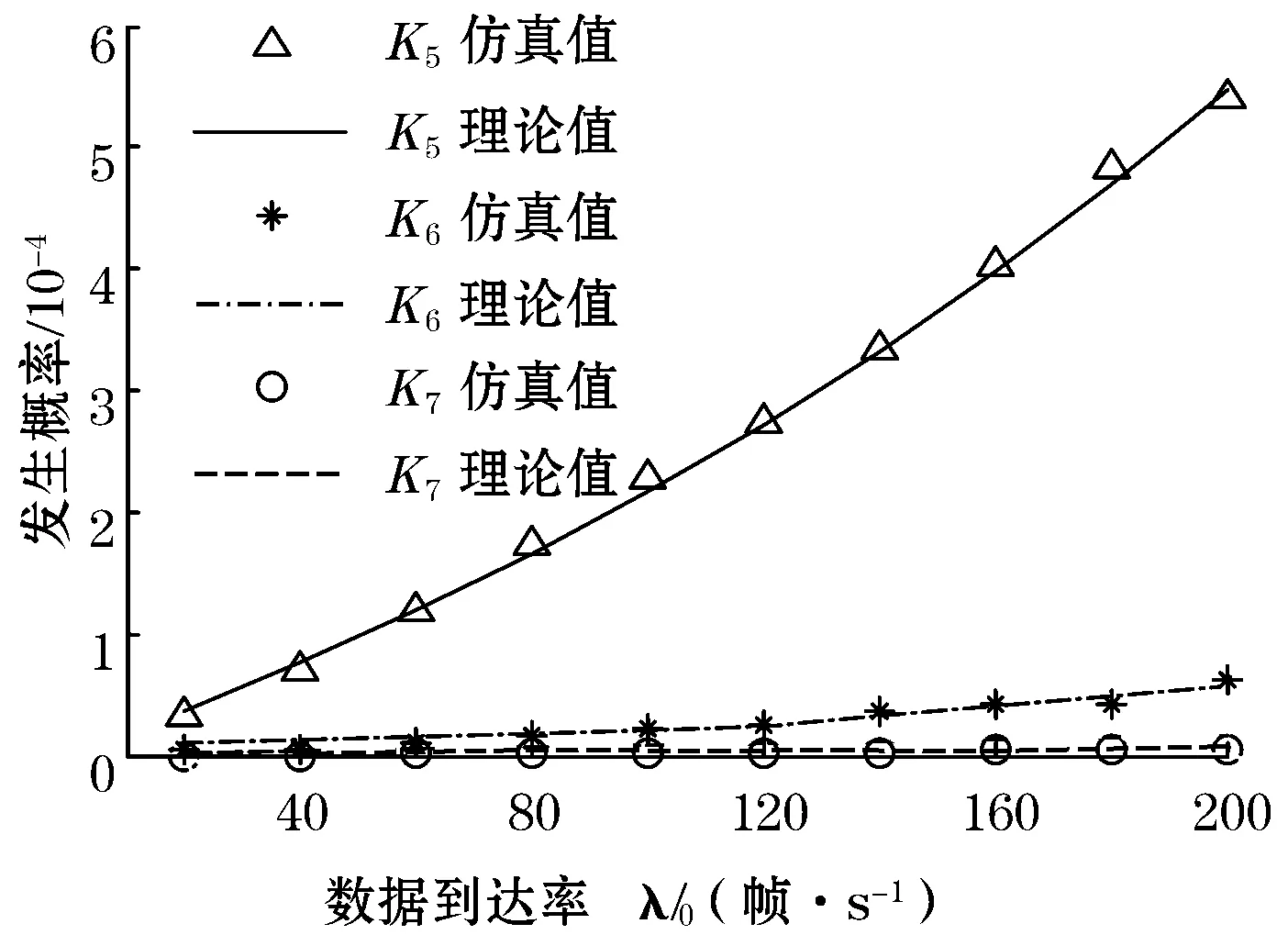
6 结论

