新型固体密度测量装置研究

高正明，贺升平，赵　娟

(1．宝鸡高新技术研究所，陕西宝鸡　721013；2．荆楚理工学院电子信息工程学院，湖北荆门 448000)

0　引言

物质密度的测量方法，根据所测量与密度的关系可分为直接法和间接法。前者是基于密度定义直接或间接测量物质的体积(质量)得到物质的密度数值，常用于性质稳定的固体密度测量，如基于阿基米德定律的静力称量法、密度瓶法、浮力计法以及气体密度天平法等，测量原理简单，测量成本较低，应用十分广泛；后者往往是通过检测与密度相关的物理量的变化来反演物质密度，如射线法[1]、超声法、光学法和振动法等[2]，间接法测量精度较高，针对性强，但测量应用范围较窄。本文根据等温状态气体的玻意尔-马略特定律，基于直接测量法提出了一种新的固体密度测量方法。

1　测量原理与方法

固体物质密度直接测量的基础是密度计算公式：

ρ=m/V

基于阿基米德定律(g为当地重力加载速)测量固体体积：

F浮=ρ液gV排

根据液体的不同有排水法、排油法、排汞法等，统称液浸法(或浸液法)，为避免液体污染，可结合气体状态方程将待测实体与测量液体进行物理隔离[3-4]。

受非接触式体积测量方法[5]启发，基于等温状态气体玻意耳-马略特定律：

ρV=C

(3)

式中C为常量。

提出一种新的固体密度的测量方法，分别采用质量测量设备和体积测量设备测量固体质量、体积，将测量数据输送至计算机/单片机，根据式计算得到固体物质密度。

1．1基于气体定律的固体体积测量方法

基于气体定律的固体体积测量原理：测试箱体体积V0，装载体积为V的待测量固体物质，并加载体积V1、初始压强p0的气体，如图 1所示。加载过程为准静态等温过程，由气体的玻意耳-马略特定律知：

p(V0-V)=p0(V0-V+V1)

(4)

即有：

(5)

式中p为加载后测试箱内的气压。

若V0、V1和p0已知，则测量得到测试箱终端压力p(或测量前后测试箱内部气体压差Δp，Δp=p-p0)，即可通过计算得到待测量固体实体体积V．

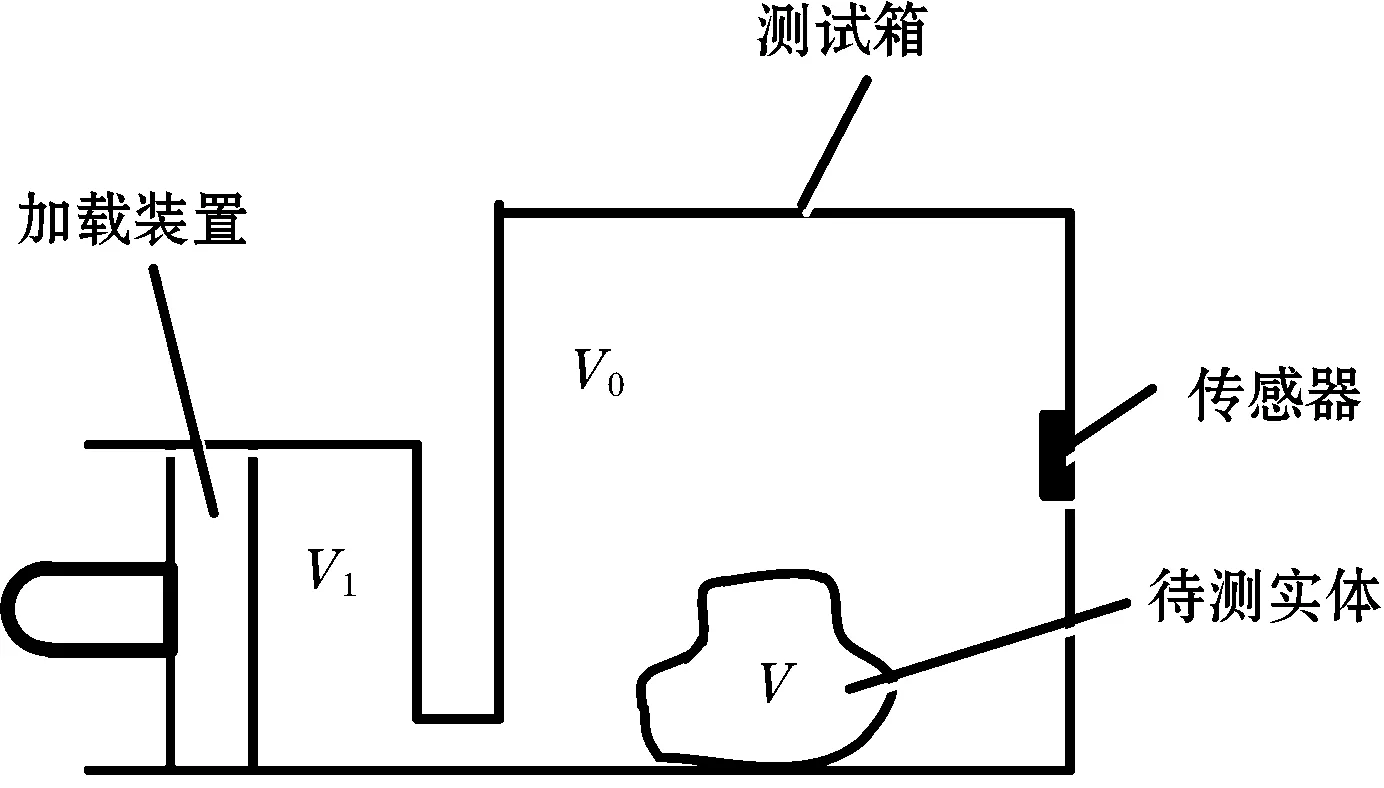
图1　测量原理图

1．2基于气体定律的密度测量原理

由以上分析可知，若预先测量得到测试箱体体积V0、加载气体体积V1和当地大气压力p0、通过压力传感器测量加载气体后测试箱内气体压力p，测试箱加载固体前后质量分别为m0、m1，则根据式(1)和式(5)可得待测固体密度ρ：

(6)

可据此设计新的基于气体定律的固体密度测量装置。

2　总体设计方案与检测流程

2．1测量装置组成

采用一体化设计原则进行结构设计，测量装置主要有3个功能模块：体积测量模块、质量测量模块和辅助系统模块，如图2所示。体积测量模块主要有测试箱、加载装置与加载气体输送管道和气体压力传感器等。质量测量模块包括测试箱、驱动装置和电子天平(或用于质量测量的压力传感器)等。辅助系统模块包括信号传输与数据处理系统、输出系统等。

图2　新型密度测量装置功能示意

2．2检测流程

检测固体密度的作业流程如下：

(1)测量装置初始化(图3(a)，图中圆台为待测实体)；

(2)通过驱动装置降下测试箱体至电子天平台，测量测试箱体质量m0，见图3(b)；

(3)抬升测试箱，装载待测实体，再次降下测试箱测量测试箱体和待测实体的质量和m1，图3(c)；

(4)抬升测试箱，连接气体管路，加载气体V1，图3(d)；

(5)卸载并恢复测量装置至初始状态(图3(e)；

(6)计算机对接收数据进行处理，给出测量报告。

3　测量指标分析

基于气体定律的固体密度测量系统采用计算机接收和处理相关数据，并可通过程控方式实现待测实体密度的批量测量，自动化、信息化程度高，测量原理简单，作业程序少，操作安全，且避免了液浸法测量过程中可能造成的液污风险。但是由于参考体积和压力的测量误差对结构的影响较大，因此测量精度与待测量实体密度范围之间存在着矛盾。

根据误差传递规律，若某测量量y是若干测量量(x1，x2，…，xn)的函数，则测量量y的误差Δy与各测量量误差Δxi(i=1，2，…，n)之间的关系为：

(7)

由式(6)可得待测实体密度的测量误差Δρ：

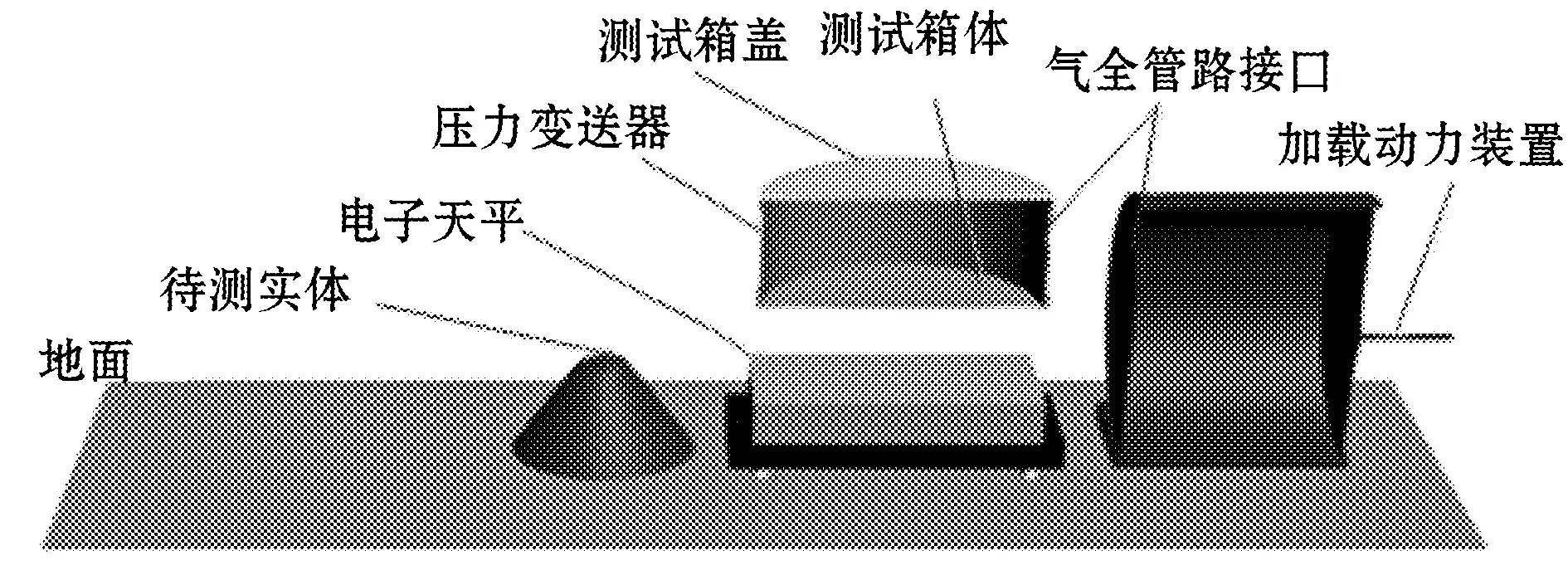
(a)初始状态

(b)测量测试箱质量m0

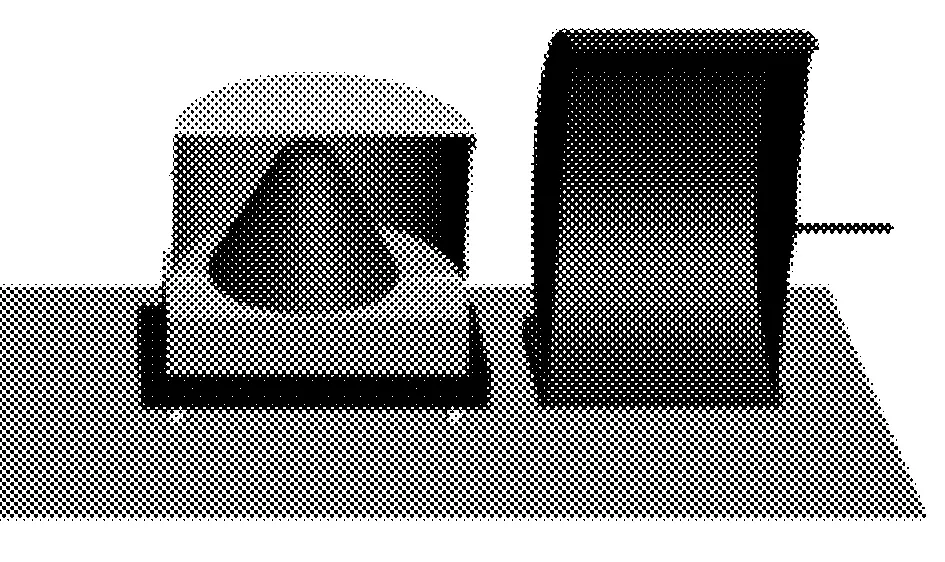
(c)抬升测量箱，放入待测量实体，随后降下测试箱测量m1

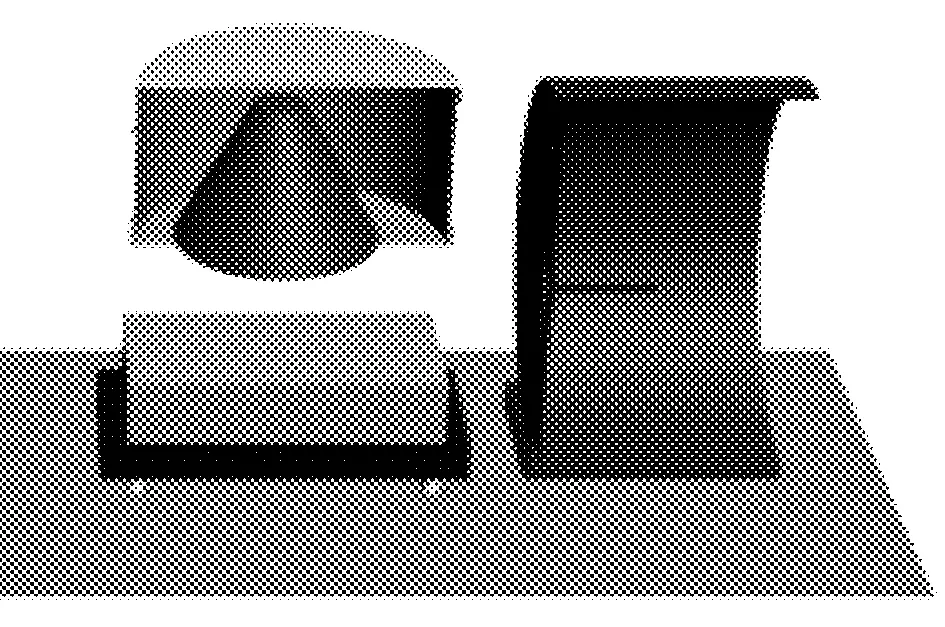
(d)再次抬升测试箱，加载气体，测量实体体积V

(e)卸载并恢复测量装置至初始状态

(8)

3．1功能模块技术指标

基于气体定律的固体密度测量的间接量包括质量、体积和气体压力。根据调研可知，质量测量相对误差可达1×10-6，如ES100K-1型电子天平，量程100 kg，测量误差1 g，因此可取电子天平的测量误差Δm=Δm1=Δm0=1 g，体积测量相对误差e1=5×10-5[6]，取ΔV0=e1V0，ΔV1=e1V1，气体压力测量误差0.01%FS．，如Gruck DPS/RPS 8000压力传感器，即e2=1×10-4，Δp0=e2p0，Δp=e2p．

3．2检测范围

由式(8)可知，固体密度的测量误差与气体压力、测量功能模块初始体积初始数值等因素相关，因此若密度的测量误差Δρ≤δ(δ为许可误差)，则若待测量物质质量m=m1-m0=100 kg或50 kg，初始压力=1．013 25×105Pa，测试箱为内径r=0．3 m，H=0．4 m的圆柱筒，则由式(8)可推知密度测量误差与待测实体体积之间的关系，如图4所示。

(a)=100 kg

(b)m=50 kg

可见：随加载气体体积的增大，误差减小，但由式(4)可知测试箱内终态压力随之升高，测试箱气密性要求增高，增大了测量装置制造与维护难度；给定初始质量，随着固体密度的增大，误差逐渐增大；待测量物质质量对测量误差的影响显著，质量越小，密度测量误差也越小，在给定测试箱箱体体积的条件下，待测物质密度必须足够小才能保证测量误差较小。若许可误差δ≤1 kg/m3，则由图4可知采用ES100K-1型电子天平时，密度的测量应满足：ρ≤2 550 kg/m3，即该测量系统的检测范围是ρ≤2 550 kg/m3。

3．3检测误差

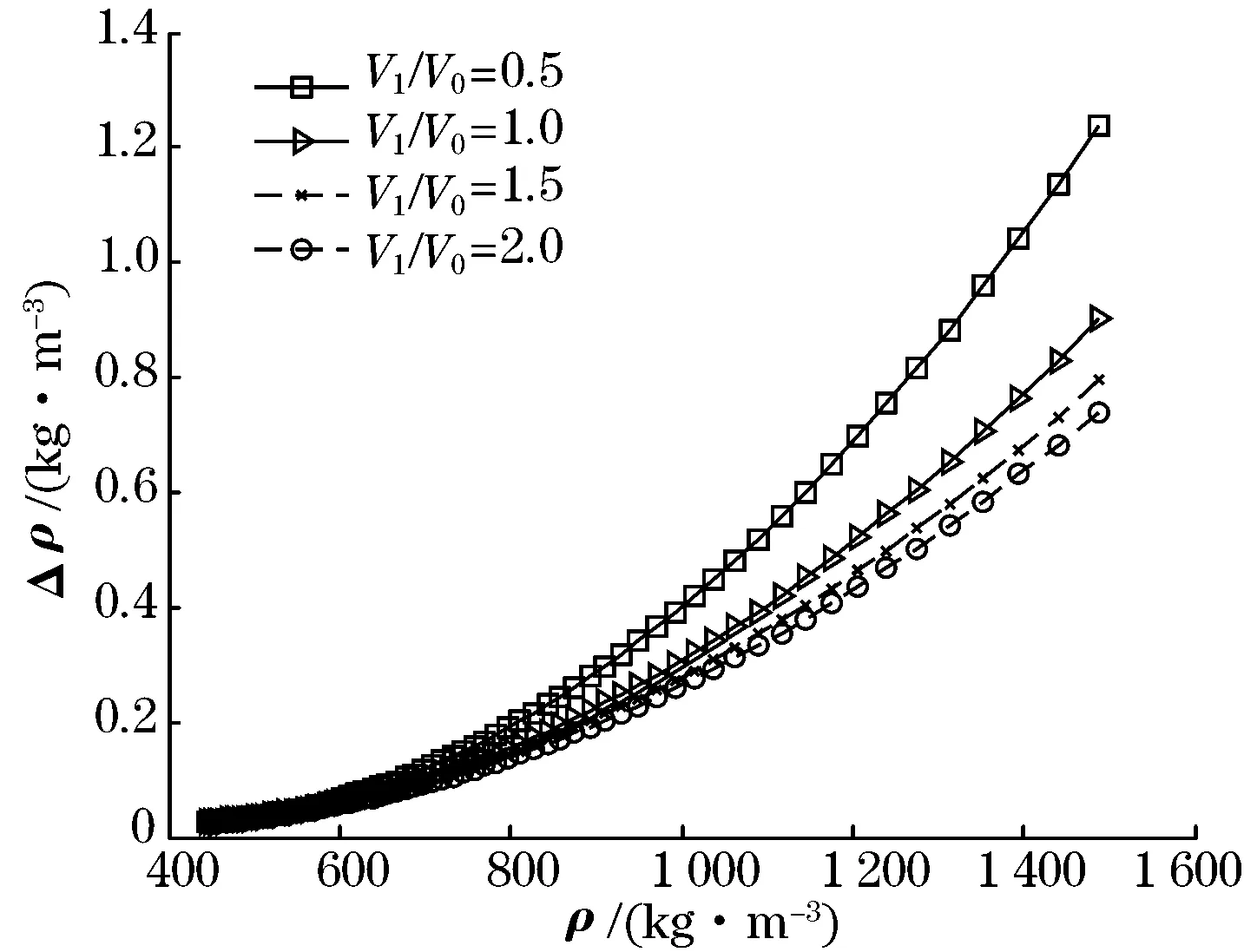
由式(8)可知，采用该装置对固体密度进行测量时，测量误差决定因素较多，其中设计阶段需要重点考虑体积、气体压力的测量误差的传递与分配，由式(8)可知，对于m=100 kg，r=0.28 m、0.25 m、0.22 m、0.20 m，h=0.38 m的圆柱实体的密度测量误差与加载气体体积之间的关系如图5所示。

可见，密度的测量误差随加载气体体积增大而减小，且密度越小的实体测量精度越高。图5还表明，测试箱放入待测实体后，剩余体积(V0-V)越小，测量精度越高，若取V1/V0=1，则测量误差Δρ小于1 kg/m3，相对误差小于0.1%，测量精度很高[7]。

4　结论

基于等温状态玻意尔-马略特定律提出了一种固体密度测量技术，分析了测量原理，设计了测量装置功能模块和检测流程，并根据误差传递理论和各功能模块调研数据确定了新型测量装置的检测范围和检测误差，分析了其优缺点和应用场合。

基于气体定律的固体密度测量装置采用计算机/单片机处理测试数据，并可通过程控方式实现待测实体密度的自动化批量测量，信息化程度高，作业程序少，测量时间短。基于ES100K-1型电子天平对测量装置测量范围进行分析，说明装置适用于ρ≤2 550 kg/m3的固体密度的检验与测量，相对误差可小于0.1%。由于该技术摆脱了传统测量方法中待测对象需要与液体直接接触的限制，避免了液污风险，减少了操作步骤，提高了待测物体安全性。

(a)m=100 kg

(b)m=50 kg

考虑到不规则实体在测试箱内摆放困难，剩余体积较大，可能造成密度测量误差偏大，因此该装置可应用于主体规则，表面可能存在缺陷或内部劣变的特定产品密度的检验，如久期贮存的易分解、潮解的固体材料等，此时可根据待测产品结构信息设计测试箱结构尺寸，提高测量精度，可作为该类物质检验、密度测量的自动化、智能化检测装置。

参考文献：

[1]魏伟胜，赵志学，鲍晓军．γ射线衰减法测量混相密度．过程工程学报，2003(6)：512-517．

[2]楚开猛．乳化炸药密度在线检测方法研究：[学位论文]．北京：北京理工大学，2008：3-11．

[3]迟善武．一种实现小体积测量的精确方法．化工自动化及仪表，1996，23 (2)：44-47．

[4]海国廷，柳玉洪．不规则物体体积测量的一种方法．宁夏大学学报：自然科学版，1995，16 (4)：32-33．

[5]李正群，计欣华．非接触体积测量实验系统．物理实验，2005，25(3)：39-41．

[6]赵朝前．力学计量．北京：中国计量科学出版社，2003：92-139．

[7]王功庆，杨锦清，曾寄萍．炮弹体内炸药密度的测定．核电子学与探测技术，1999，19(3)：172-177．