局部不变特征匹配的并行加速技术研究

王灿进，孙 涛，陈 娟

（1.中国科学院 长春光学精密机械与物理研究所激光与物质相互作用国家重点实验室，吉林 长春130033；2.中国科学院大学，北京100049）

1 引 言

图像匹配是指在不同视点的两幅图像中寻找对应的同名点，以确定两幅图像之间的空间变换关系的过程，其在图像检索［1］、宽基线匹配［2］、图像配准［3－5］、目 标 识 别［6－8］、全 景 图 拼 接［9］、星 点 匹配［10］、电子稳像［11］、三维重建［12］等领域得到广泛的应用。就目前的匹配技术而言，主要分为基于灰度的图像匹配方法和基于特征的图像匹配方法。基于灰度的匹配方法对于噪声和光照的鲁棒性较弱，已逐渐不再使用。

基于特征的图像匹配方法中，局部不变特征因对于光照变化、由目标和相机相对运动引起的图像模糊、噪声、遮挡有很好的鲁棒性，对于透视变换、尺度缩放等具有不变性而得到广泛的使用。局部不变特征在近十年来发展迅速，著名的算法包括2004年Lowe提 出 的SIFT［8］、2007 年Bay提 出 的SURF［13］、2010 年Calonder 等 提 出 的BRIEF［14］，2011 年Stefan 等 提 出 的BRISK［15］、Rublee等提出的ORB［16］、2012年Alahi等人提出的FREAK［17］等。SIFT 和SURF 的特征点检测过程都是对LOG 算子的近似加速，生成特征向量时，SIFT 计算的是采样点周围的梯度方向直方图，而SURF计算的是Haar特征的累加和，最后计算特征向量的欧式距离进行匹配。而BRIEF等算子则采用不同的采样模式，生成二进制描述子，依靠计算汉明距离（异或）进行匹配。尤其是FREAK 算子，其采样点的模式接近于人类视网膜（Human Retina）的拓扑结构，在匹配过程中模拟人类视觉的扫视搜索，取得了很好的性能。模拟人类视觉系统是目前计算机视觉的一个重要的发展方向。为此本文首次将FREAK 算子应用在图像匹配中，取得快速有效的配准结果。

然而当图像像素数目增大或者背景变得复杂时，提取出的特征点增加，特征向量的生成和匹配的时间也随之增加，使局部不变特征算法尤其是SIFT 和SURF难以运用在实时系统中。根据局部不变特征的局部性和特征点检测、特征向量生成和特征向量匹配3个过程的独立性，本文提出一种并行处理的机制对局部不变特征算法进行加速：对待匹配图像进行有重叠的分块，对于每一块子图像在新的线程中进行特征点的检测、特征描述向量的生成和特征向量的匹配；对于特征点的检测、描述向量的生成和特征向量匹配过程也可并行在3个线程中同时处理。这样的并行处理机制能够大大加速局部不变特征描述方法的计算过程，在多核PC 机上实验表明本文方法可以在保证匹配精度的同时大大缩短匹配时间。

2 FREAK 特征描述子

本文主要采用经典的SIFT、SURF算法和最新的FREAK 算法进行实验。3种算法均主要均包括3个步骤：感兴趣点检测、特征向量的提取和特征向量匹配。SIFT 和SURF的算法过程不加赘述，重点介绍FREAK 描述子。

2.1 FAST感兴趣点检测

FAST 算子是近年来发展出的一种新的角点算子［18］，因为其快速性被广泛采用。将FAST 算法推广到尺度空间，就可以用于FREAK 局部不变特征算法的特征点检测。FAST 特征点定义如下：在以当前像素为圆心，3.4个像素为半径的圆上的16个像素中，若至少有9个连续的像素比中心像素亮或者暗，则当前像素就是一个FAST 特征点（如图1所示）。

首先建立尺度空间金字塔。尺度空间金字塔包含n 层（octaves）ci和n 个内层（intra－octaves）di，i＝0，1，…，n－1，实验中n 取4。c0为原始图像，d0由c0降采样1.5倍得到。ci由ci－1隔半采样得到，di也是由di－1隔半采样得到，di位于ci和ci＋1之 间。假 设t 表 示 尺 度，则t（ci）＝2i，t（di）＝2i×1.5。

在每层找到FAST 特征点作为候选特征点，对于这些点计算其FAST 得分s：

式中：Ip表示中心像素值，Ii表示中心点周围比Ip像素值大的连续区域的像素值，Ij表示中心点周围比Ip像素值小的连续区域的像素值，τ是固定的阈值。

图1 多尺度FAST 特征检测算子Fig.1 multi－scale FAST detector

接着使用FAST得分对这些点在尺度空间进行非极大值抑制：特征点的s在同一层和相邻上下层中必须大于它的26邻域。对于满足这些条件的点，在图像和尺度的三维连续空间进行插值和连续尺度细化：首先对相邻三层的FAST得分块拟合成二次函数，得到3个细化的极大值位置。接着对这些细化的得分沿着尺度轴拟合成抛物线，在抛物线的极值点得到其得分和尺度的估计值。最后在真实尺度附近的层上对得分块的坐标进行插值，就得到最后的特征点的精确位置和真实尺度。这样得到的像素位置具有亚像素级的定位精度。

2.2 特征描述子的生成

FREAK 描述子模拟人类视网膜的模型，建立了如图2所示的采样结构。

图2 FREAK 算子的采样点结构Fig.2 Illustration of the FREAK sampling pattern

图2中，每个圆心代表一个采样点，圆代表感受域的范围，离中心点越远，模糊的高斯核半径越大，并且采样点感受域之间有重叠。

最终生成的FREAK 描述子是二进制比特串，由采样点对的感受域强度比较结果级联而成。假设F 为描述符，则：

式中：Pa是感受域对，N 是描述子的维数

式中：I（Pr1a）是感受域平滑后的强度。

假设采样点数为N，则最终可以生成的描述子一共有C2N维。一些维度包含的信息量较大，而其余维度包含的信息量较小。为选出信息量较大的维度，首先计算每一维的方差，挑选出方差最大的那一维，计算剩下维度和它的协方差，保留协方差最小的那一维，以此类推。实验证明保留下的点对都是由外围的采样点对构成，这和人类视网膜周边区识别目标的轮廓这一特性是一致的［19］。

2.3 特征向量的匹配

对于SIFT 和SURF 算法，一般是采用计算欧式距离，随后采用最近邻和次近邻的比值来确定匹配点。

式中：r为事先确定的阈值。

FREAK 算子生成的是0和1组成的二进制描述符，描述符之间的距离采用汉明距离计算，即异或操作。当2个描述符之间的汉明距离小于阈值T 时，认为其是匹配的一对特征点。可以先比较前16个比特的汉明距离，随后使用后面的比特进行精确匹配。因为越是靠前的特征维度，越能提供大量的信息，通过前16个比特已经可以去除90%以上的误匹配点。这种匹配方法和人类视觉的扫视模型也很类似，也就是先在场景中确定目标的位置和轮廓，再进行精确判断。

最后使用RANSAC 算法消除错误匹配。RANSAC 是一种模型假设检验方法［20］，使用较少的初始数据构建模型对全部数据进行正确筛选，其对于噪声和特征点提取误差都具有较强的鲁棒性。

待配准图像间的仿射变换关系可以由如下的方程表示：

确定方程中的6个参数，至少需要3对匹配点。相应的RANSAC检验步骤如下：

（1）在距离筛选之后的匹配点中任意找出3对，计算变换参数（M，T）；

（2）对于剩下的每一对变换点（xi，yi）（ui，vi），将（xi，yi）通过变换矩阵计算出（u）。如果｜｜＜ε，｜vi’－vi｜＜ε，则认为这一对点满足变换参数（M，T），将计数count加1。（3）另外选取三对点，重复（1）、（2）。

（4）计算若干次后，选择count次数最大的参数（M，T）为最终变换参数，满足该参数的点集为正确匹配的点集。

3 利用多线程进行分块加速

SIFT、SURF、FREAK 方法对于特征点的检测、特征向量的提取都仅仅使用了特征点局部的灰度信息。为此把图像分成大小合适的块，将不会影响上述步骤的执行。对每一个分块得到的子图像而言，其计算速度比源图像要快得多。例如对于实验中的512×512 的graffiti图像，SURF平均匹配时间大约为1 160ms，而一幅300×300的图像使用同样的算法，时间可以缩短至480ms左右。这种采用同一程序的多个实例在不同数据上运行的方法，称为单程序多数据（SPMD）计算模型。这样均匀的数据划分能保证各个线程之间的负载平衡。

对于SIFT，需要使用3σ的邻域像素计算主方向，使用16×16的正方形计算特征向量。如果分割之后一个特征点恰好在子图像的边缘，那么其邻域值会受到影响。为此分割图像需要有重叠的部分，重叠尺寸为τ个像素。对于SIFT 取τ＝16。对于SURF，计算主方向的邻域为6σ，生成特征向量的邻域为20σ 的正方形，如果Hessian金字塔有四组四层，那么20σ的最大值为520，如果重叠部分取这么大，则分块已经没有意义。考虑到不同位置的部分需要进行高斯加权，取重叠部分为高斯函数系数3.3σ 的最大值86。而对于FREAK 描述子，τ 的大小取决于采样点的个数。注意分块不能太小，否则会使特征点的提取和特征向量的计算都不准确。对于512×512的图像可以分为大小相等的四块，每块为（512＋86）／2＝299，实验中取为300。图像的重叠分块如图3所示。

图3 图像重叠的分块Fig.3 Image overlapping division

4 局部特征处理的流水线技术

流水线技术是目前微处理器常用的加速技术，它将一条指令分为取指令、调度、译码、取操作数、执行以及存储等阶段，每个时钟周期MCU 的不同部件处理多个指令的不同阶段，这样处理器可以在一个时钟周期内同时执行多条指令，即并行处理。

局部图像特征算子分为特征点的检测、特征向量的提取和特征向量的匹配3个阶段。每个阶段是相对独立的，只需要用到前一阶段的结果即可。这类似于计算机的一条指令的3个阶段。为此可以采用类似流水线的技术并行执行。具体过程如下：

（1）为特征点的检测、特征向量的提取和特征向量的匹配3个阶段各单独开辟一个线程，分别记为Thread1，Thread2和Thread3。

（2）在Thread1中，每检测出一个特征点，将特征点的位置和尺度交给Thread2，并打开Thread2，Thread2据此计算出该特征点对应的特征向量，计算完毕暂停Thread2。

（3）Thread2 每计算出一个特征向量，交给Thread3，和预先提取出的模板图像的特征向量集进行匹配，匹配完毕暂停Thread3。

流水线示意图如图4所示。

图4 局部不变特征匹配的流水线技术Fig.4 Pipelining of local invariant feature matching

假设3个过程所用的时间均为T，那么处理一幅图像需要时间为3T，串行处理3幅图像需要时间为9T，而采用图中所示流水线技术3幅图像只需要5T。但是特征点检测、特征描述和特征点匹配耗时不一致，会导致线程等待，造成一些微小的时间损耗。

5 实验结果

在Intel Core2Quad 4核处理器，内存2G，主频2.67GHz，操作系统windowsXP环境下使用VC2008结合Opencv 类库编程实现。从PASCAL数据库中选择旋转和尺度缩放、亮暗和视角变化的3组图像进行匹配实验如图5所示。将图像统一转化为512×512的大小，首先提取出变换之前的图像的特征向量集作为模板，存储在全局数据空间，所有的线程对该数据都有只读权限。运行时只对变换后的图像进行处理，这样便于比较匹配结果。

5.1 采用4分块的匹配结果

对于SIFT、SURF和FREAK 方法分别进行4个有重叠的分块加速，对于SIFT，τ取16，对于SURF，τ取86，FREAK 算子τ 取50。实验结果如表1～表3所示。

从表1、2、3可见，FREAK算法的运算时间要远远小于其余两种算法。对于第一幅图像，分块前SIFT和SURF算法耗时是FREAK 的44.2和7.7倍，分块后是FREAK算法的35.5和6.6倍。

表1 SIFT匹配分块前后性能比较Tab.1 Performance of SIFT before and after blocking

表2 SURF匹配分块前后性能比较Tab.2 Performance of SURF before and after blocking

续表

表3 FREAK 匹配分块前后性能比较Tab.3 Performance of FREAK before and after blocking

SIFT 的 最 大 加 速 比 达 到2.51，SURF 的 最大加速比达到2.42，FREAK 的最大加速比达到2.02。并且可以看出检测出的特征点数越多，处理时间越长，加速比越大。理论上最大能达到的加速比应该等于线程数4，但是由于分块之间有重叠以及四幅子图像的处理时间不可能完全一致造成线程等待，导致加速比的下降。

从表格看出分块后的特征点数和匹配点数均增加，这是因为在重叠区域有可能两个子图像在同一位置均检测和匹配出特征点，但这种重复不会影响匹配结果。但分块不可避免的会导致靠近分块边缘的特征点邻域发生变化，解决方法是加大重叠尺寸τ。

5.2 采用流水线的匹配结果

采用流水线技术进行加速。结果如表4所示。

SIFT 的 最 大 加 速 比 达 到2.07，SURF 的 最大加速比达到2.21，FREAK 的最大加速比达到2.16。同样处理时间越长，加速比越大。

表4 流水线处理前后结果比较Tab.4 Comparison of matching result before and after pipeling

采用流水线技术只是调整了计算顺序，使3个过程可以并行执行，并没有影响特征点检测和特征向量生成的数据，因此只是加速了处理时间，匹配结果完全一致。此处的耗时可以认为是整个图像在特征点检测、特征描述子计算和特征点匹配这3个过程所用的最大时间。经过测试，对于SIFT 这个时间与描述向量的匹配时间相当；而对于SURF 和FREAK，这个时间与特征描述子计算的时间相当。这证明对于SIFT 方法，匹配是3个步骤中最耗时的过程；而对于SURF 和FREAK，特征描述子的计算是3个步骤中最耗时的过程。

5.3 采用不同分块的比较

对于采样成512×512大小的图像，可以划分为k2（k＝1，2，…）块，划分的块数越多，每块图像越小，单块的处理时间越短。但是一方面由于处理器硬件的限制，能同时执行的线程数有限，线程再多只能由操作系统调度分时间片执行。另一方面由前面的分析可知，分块变小对于其邻域有影响，提取的特征点数量和位置都会有变化。如果分块很小甚至会提取不出局部特征点。采用图5（C）进行实验。

图5 实验图像Fig.5 Experimental images

从图6可以看到在k＝2时，运行时间下降得最快。而随后k＝3到8之间3种算法均略有下降，SIFT 算法在k＝8之后处理时间会上升。这是因为使用的处理器为4核，若分块数大于4，一个线程将串行处理多个分块，虽然每个分块的处理时间减少，但这多个分块叠加起来却比4分块时要大，再加上由于线程之间的通信以及线程的启动停止等步骤会耗去一部分的时间，因此处理时间增加。

图6 运行时间与分块数的关系Fig.6 Relationship between the running time and the number of sub－block

分块增加，重叠的部分累加起来也会增加，导致重复检测和匹配的特征点增多。为了验证检测出的特征点的有效性，若不同分块检测出的特征点距离小于3，则认为是相同的特征点，只取其中之一。最终匹配的特征点如图7所示。

可见3种算法随着分块的增加匹配点数都会下降，而SURF在k＝7以后匹配点数变为0。这是因为分块增加，则会有更多的特征点的邻域提取不完整，特征向量的计算出现误差最后导致匹配的失效。相比较之下SIFT 算法邻域较小，对于分割的鲁棒性更好。

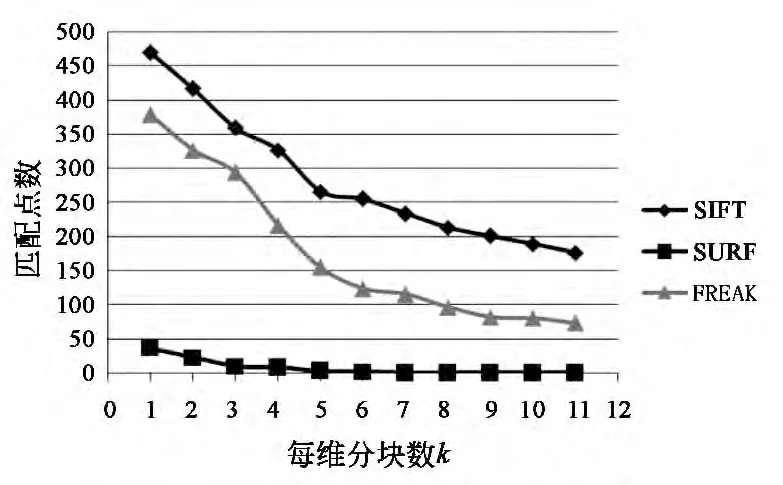
图7 匹配特征点数与分块数的关系Fig.7 Relationship between the number of matching feature points and the number of sub－block

由以上分析可知，时间性能并不是始终随着分块的增加而减小的，而是要考虑处理器的硬件配置，而匹配性能随着分块的增加会有所下降。为此在运行时间足够小的前提下取尽量小的分块数目，以保留足够多的有效特征点进行匹配。在本文实验中4分块是比较好的选择。

6 结 论

为了解决传统的局部特征描述子对大尺度图像匹配过于耗时的问题，本文首先引入一种新的FREAK 局部不变特征，其次提出使用并行计算的思想为局部不变特征算法进行加速，即大图像分块的并行计算和特征点检测、特征向量生成和特征向量匹配过程的流水线技术。作为一种具有人类视觉模型结构的二进制描述子，FREAK 算法拥有良好的计算实时性和匹配准确性。而对SIFT、SURF 和FREAK 算法的实验证明本文的并行计算思想能够取得较好的加速效果。

这种并行思想同时也适用于其他的模式识别算法，例如模板匹配、Haar特征分类等。当单个PC机无法满足硬件要求时，可以组建局域网计算，通过共享内存或者以消息传递的方式进行通信。推广到嵌入式系统上，可以采用多个DSP芯片并行执行。这里需要考虑并行处理的粒度，并不是粒度越小越好，因为识别算法需要使用周围像素的信息，粒度太小可能导致信息的丢失，同时线程之间的相互通信也会增加处理时间。为此在算法的分解上需要综合考虑处理时间和算法有效性二者之间的平衡。这种并行的思想为图像处理算法的加速提供了一种通用的思路。

［1］ Mikolajczyk K，Schmid C.Indexing based on scale invariant interest points［C］∥8th IEEE International Conference on Computer Vision，Montbonnot，France：ICCV，2001：525－531.

［2］ Tuytelaars T，Gool L.Matching widely separated views based on affine invariant regions［J］.International Journal of Computer Vision，2004，59（1）：61－85.

［3］ 刘向增，田铮，史振广，等.基于FKICA－SIFT 特征的合成孔径图像多尺度配准［J］.光学精密工程，2011，19（9）：2186－2196.Liu X Z，Tian Z，Shi Z G，et al.SAR image multi－scale registration based on FKICA－SIFT features［J］.Opt.Precision Eng.，2011，19（9）：2186－2196.（in Chinese）

［4］ 赵立荣，朱玮，曹永刚，等.改进的加速鲁棒特征算法在特征匹配中的应用［J］.光学精密工程，2013，21（12）：3263－3271.Zhao L R，Zhu W，Cao Y G，et al.Application of improved SURF algorithm to feature matching［J］.Opt.Precision Eng.，2013，21（12）：3263－3271.（in Chinese）

［5］ 苏可心，韩广良，孙海江.基于SURF 的抗视角变换图像匹配算法［J］.液晶与显示，2013，28（4）：626－632.Su K X，Han G L，Sun H J.Anti－Viepoint Changing image matching algorithm based on SURF［J］.Chinese Journal of Liquid Crystals and Displays，2013，28（4）：626－632.（in Chinese）

［6］ 贾平，徐宁，张叶.基于局部特征提取的目标自动识别［J］.光学精密工程，2013，21（7）：1898－1905.Jia P，Xu N，Zhang Y.Automatic target recognition based on local feature extraction［J］.Opt.Precision Eng.，2013，21（7）：1898－1905.（in Chinese）

［7］ 李英，李静宇，徐正平.结合SURF 与聚类分析方法实现运动目标的快速跟踪［J］.液晶与显示，2011，26（4）：544－550.Li Y，Li J Y，Xu Z P.Moving target fast tracking using SURF and cluster analysis method［J］.Chinese Journal of Liquid Crystals and Displays，2011，26（4）：544－550.（in Chinese）

［8］ Lowe D.Distinctive image features from scale－invariant keypoints［J］.International Journal of Computer Vision，2004，60（2）：91－110.

［9］ Brown M，Lowe D.Automatic panoramic image stitching using invariant features［J］.International Journal of Computer Vision，2007，74（1）：59－73.

［10］ 翟优，曾峦，熊伟.基于不变特征描述符实现星点匹配［J］.光学精密工程，2013，20（11）：2531－2539.Zhai Y，Zeng L，Xiong W.Star matching based on invariant feature descriptor［J］.Opt.Precision Eng.，2013，20（11）：2531－2539.（in Chinese）

［11］ 吴威，许廷发，王亚伟，等.高精度全景补偿电子稳像［J］.中国光学，2013，6（3）：378－385.Wu W，X T F，Wang Y Wet al.High precision digital image stabilization with full frame compensation［J］.Chinese Optics，2013，6（3）：378－385.

［12］ Noah S，Steven M，Richard S.Photo tourism：exploring photo collections in 3D［J］.ACM Trans on Graphics，2006，25（3）：835－846.

［13］ Bay H，Tuvtellars T，Gool V.SURF：speeded up robust features［C］∥Proceedings of the European Conference on Computer Vision，Graz，Austria：ECCV，2006：404－417.

［14］ Calander M，Lepetit V，Strecha Cet al.BRIEF：Binary robust Independent elementary features［C］∥European Conference on Computer Vision，Crete，Greece：ECCV，2010：778－792.

［15］ Stefan L，Margarita C，Roland S.BRISK：binary robust invariant scalable keypoints［C］∥Proceedings of the IEEE International Conference on Computer Vision，Barcelona，Spain：ICCV，2011：2548－2555.

［16］ Rublee E，Rabaud V，Konolige K，et al.Orb：an efficient alternative to sift or surf［C］∥Proceedings of the IEEE International Conference on Computer Vision，Barcelona，Spain：ICCV，2011：2564－2571.

［17］ Alahi A，Ortiz R，Vandergheynst P.FREAK：FAST Retina keypoint［C］∥Computer Version and Pattern Recognition，Providence，RI，USA：CVPR，2011：510－517.

［18］ Rosten E，Drummond T.Machine learning for highspeed corner detection［C］∥9th European Conference on Computer Vision，Graz，Austria：ECCV，2006：430－443.

［19］ Field D，Gauthier J，Sher A，et al.Functional connectivity in the retina at the resolution of photoreceptors［J］.Nature，2010，467（7316）：673－677.

［20］ 龚卫国，张璇，李正浩.基于改进局部敏感散列算法的图像匹配［J］.光学精密工程，2011，19（16）：1375－1383.Gong W G，Zhang X，Li Z H.Image registration based on extended LSH ［J］.Opt.Precision Eng.，2011，19（6）：1375－1383.（in Chinese）