直圆柱管科氏质量流量计测量误差分析

李　兵，魏玉兰

(湖州师范学院信息与工程学院，浙江湖州　313000)

0　引言

在现代化生产中，直圆柱管被广泛使用在各种工业领域中[1-3]。圆柱管内液体流动会造成管道的振动，对其固有频率产生影响，流速越快，管道的固有频率越低。根据该特性可修改影响圆柱管固有频率的参数以降低其振幅，避免造成破裂。此外，液体在圆柱管内流动能产生科氏力，将影响管道的振动特性，通过分析管道的振动信号可计算出液体的质量流量，从而判其是否存在堵塞，这种测量装置称为科氏质量流量计。对于科氏质量流量计的数学模型、试验测量、非线性振动等方面具有一定的研究[4-7]，但对其测量数值的误差分析研究较少。以两端固支薄壁直圆柱管为试验对象，使用科氏质量流量计的原理和测量方法，结合理论和试验分析，从试验装置结构、传感器布置、激振力、激振频率等多个方面分析造成误差的原因，并给出减小误差的措施。

1　基本理论

1．1科氏质量流量计

液体在直圆柱管内流动会产生科氏力，会影响管道的振动特性。在一根两端固定的管道中间处施加激振力，当管道内液体静止时(流速为零)，管道的振动是以中点为对称点的同向振动。当流速不为零时，产生的科氏力导致前半段管道振动角速度降低，而提高了后半段圆柱管的振动角速度。从而造成两侧对称点处的振动存在相位差，该相位差与管道内液体的质量流量成正比。

当管道内的液体以速度v流动时，同时在管道中点处施加一激振力F，管道会产生科氏力载荷积度[8-9]。由于直圆柱管以中点对称，所以载荷积度以中点对称相反，导致两对称点处的位移大小一样、方向相反。则可通过方程(1)获得圆柱管内流体的质量流量Qm:

(1)

式中：E为弹性模量；I为转动惯量；ω为激振力F的角频率；Y(x)为管上任一点的位移，其大小仅与检测点所在位置有关；α为振动响应信号间的相位差。

1．2运动方程

为了分析影响直圆柱管科氏质量流量计测量精度的因素，可通过分析含流体圆柱管道的运动方程及其解获得。可将含流体圆柱管化为管微元和流体微元进行分析，如图1和图2，可得非线性运动方程[4]：

(2)

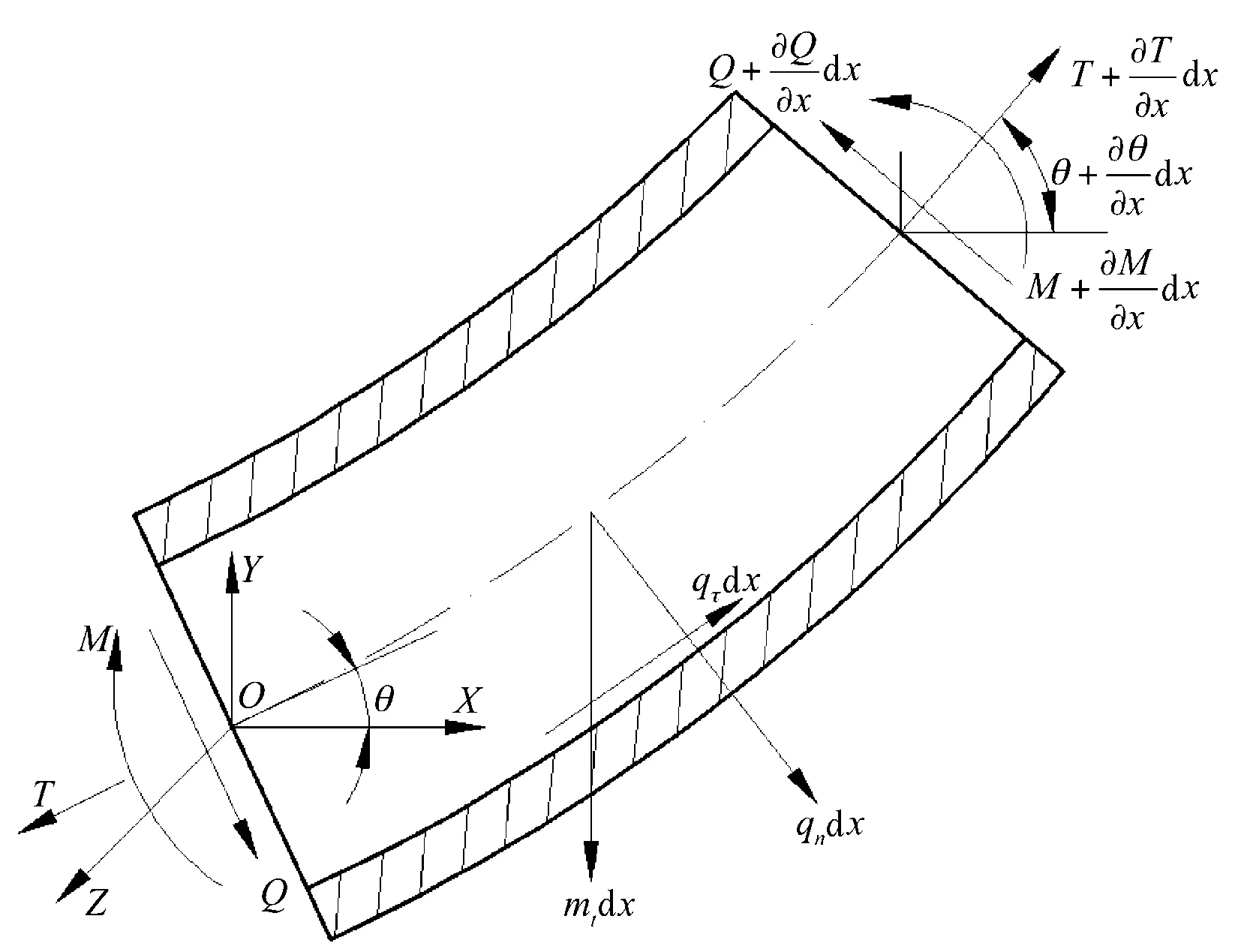
图1　管微元

使用Galerkin法对式(2)离散化处理，正交后去掉非线性项，当只考虑一个模态时，则解为式(3):

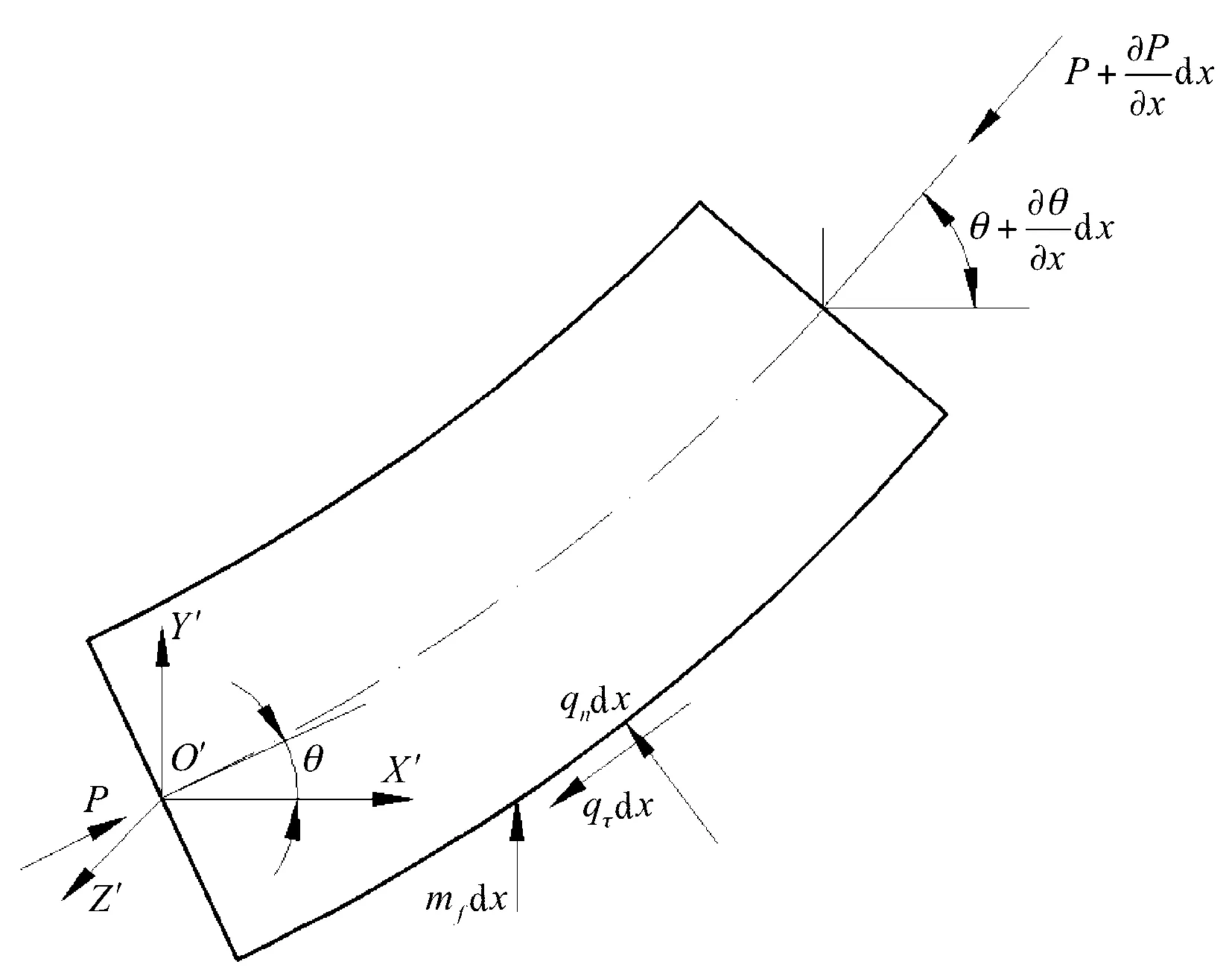
图2　流体微元

(3)

2　试验装置与方法

为保证试验过程中的稳定性，试验装置被固定在试验平台上，如图3。为保证外加激振的均匀性和对称性，把激振器安装在圆柱管的中心。圆柱管上的6个应变片传感器以圆柱管中点对称均布安装。圆柱管道的约束方式为两端固定，试验系统分为激振部分和信号采集处理部分[3]。管道内液体采用自来水，水压为0.02×106N/m2，使用电子天平测量可获得其密度为1.0×103kg/m3．

图3　试验系统

具体试验步骤如下：首先，需要先获得液体流动时圆柱管的振动响应曲线；其次，获得流速等于零时圆柱管的振动响应曲线；最后，分析两个响应曲线的相位可获得相位差，使用式(1)可计算出其内部的质量流量[9]。

3　试验分析

在圆柱管内分别使用3种不同的流量进行试验，分析前三阶振动响应曲线，可得圆柱管的固有频率，见表1。

从表1可得，液体的流量大小影响圆柱管的固有频率，减小流量使固有频率提高，增大流量使固有频率降低[9]。由于直圆柱管各处截面大小相同，流量小意味着流速小，即圆柱管的固有频率受流速大小影响。

表1　不同流量时的固有频率

通过分析响应曲线可获得振动响应的相位差[9-10]，通过计算即可获得质量流量。由于科氏力对圆柱管一阶振动影响最大，且容易测量，选用两个对称点的一阶振动响应曲线进行分析计算，即选用2号和5号应变片传感器，分别位于左右端面163 mm处，α2，5为该两点振动响应的相位差。直圆柱管参数如下：长度l=831 mm，壁厚n=0.4 mm，密度ρ=7.62×103kg/m3，外径D=24.875 mm，内径d=24.075 mm，截面积A=0.307 4×10-4m2,其中检测点位置常数Y(x)=0.001 010 147 98，圆柱管弹性模量E=1.95×1011N/m2，I=0.230 9×10-8m4．分别选用2种不同的流量对其进行计算，见表2。

表2　质量流量试验结果

从表2可看出，使用该种方法得到的质量流量与实际值接近，但存在误差。

4　误差分析

通过试验分析，使用该方法得到的质量流量与实际值之间存在误差。由于理论计算是在理想的状态下，但被测圆柱管的直径与壁厚的不均匀性和自身存在焊缝导致了圆柱管的几何特性发生变化。此外，为在两固定端实现密封采用了橡胶垫片，导致不能达到完全固定的约束方式。圆柱管上的传感器不能完全对称，测量仪器也存在测量精度误差。从而使试验获得的质量流量与实际值不同。此外，激振力、激振频率、管道内的压力也会造成测量误差。

4．1激振力对测量误差的影响

根据式(1)，计算质量流量与激振力的大小无关，但在液体静止和流动试验时所采用的激振力大小必须相同，否则会造成测量误差。通过试验可证明此结论，见表3。在实际测量中，由于激振力不是十分稳定，会造成较小的偏差。通过表3可看出，在相同的激振频率和流量下，使用不同的激振力，试验获得的质量流量与实际质量流量相接近，误差不会超出3.24%，在允许范围内。还可看出，在流量高时的测量误差比流量低时的测量误差小。

表3　不同激振力下的误差

4．2激振频率对测量误差的影响

测量误差不但受激振力大小的影响，还受激振频率大小的影响。根据式(3)，在相同激振力、不同激振频率作用下，圆柱管的振动响应是不一样的，会对质量流量的计算造成误差。由于试验过程中激振器输出激振频率的最高精度为0.02 Hz，所以只考虑0.02 Hz的测量误差。

当液体以39 kg/min流动时，圆柱管一阶固有频率为fn=89.263 9 Hz，令激振频率为f1=88.119 5 Hz，则激振频率的变化范围为f2=(88.119 5±0.02)Hz，t=1，根据式(3)可得：

(4)

式中：ωn为圆柱管道的固有角频率；Ω1为激振角频率；Ω2为变化的激振角频率。

从式(4)可得，当液体以39 kg/min的流量流动时，激振频率变化0.02 Hz，圆柱管的振动响应变化了1.6%。从而可得，激振频率的变化能造成测量误差。为减少该误差，应先测量水流动时的振动响应信号，然后在不改变激振频率和激振力的情况下使水停止流动，并测量液体静止时的振动响应信号，这就可保证水静止和流动时的激振频率大小相等。由于试验采用Agilent的33220A函数/任意波形发生器，其输出频率比较稳定，所以不用考虑激振频率突变所造成的误差，只考虑激振频率的大小即可。通过试验可证明该结论，见表4。通过表4可得，激振频率的变化对质量流量的测量产生影响。在相同的激振力和流量下，使用不同的激振频率所得到计算质量流量与理论质量流量相接近，误差不超出2.56%，在允许范围内。离共振频率点的两侧越远，试验测量误差越小。此外，试验过程中，在共振点处的测量值与实际值偏差较大，见表5，最大误差已达到52.05%。

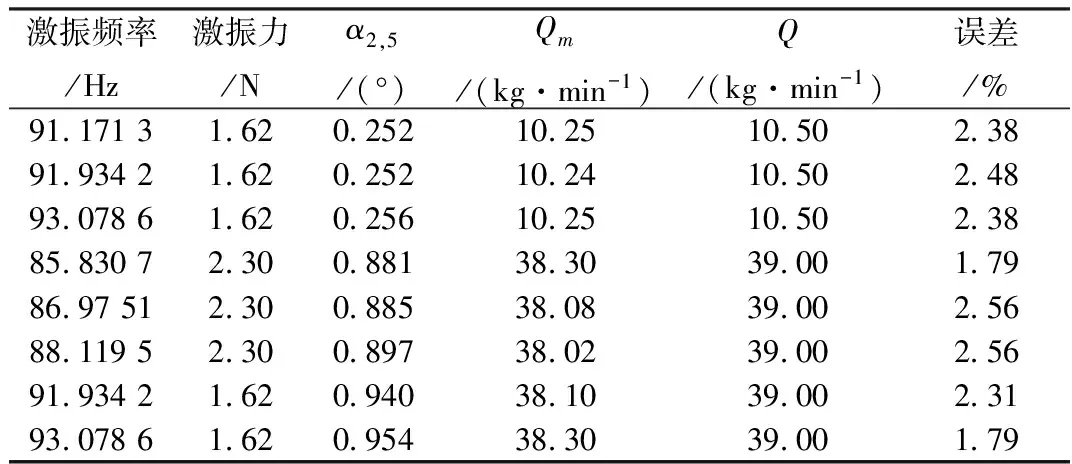
表4　不同激振频率下的误差

表5　共振点处的误差

4．3激振频率的选用范围

在共振点测量得到的质量流量与实际值有很大误差且无规律。根据式(4)可得，液体静止时圆柱管的振动响应为yj，液体流动时圆柱管的振动响应为yl，当激振频率Ω等于液体静止的圆柱管固有频率时，式(4)可变为：

(5)

从式(5)可得，当激振频率Ω等于液体静止的圆柱管固有频率ωj时，yj值是不稳定的。同理可得，当激振频率Ω等于液体流动的圆柱管固有频率点ωl时，yl值也是不稳定的。液体静止时和流动时圆柱管的固有频率并不相同，在这两个固有频率点不能测量到准确的相位差，从而不能获得准确的质量流量。所以在选择激振频率时应避免液体静止和流动时圆柱管的固有频率点。由于该圆柱管在液体静止时的固有频率点和液体流动时的固有频率点比较接近，所以在试验中不选用这两个固有频率点之间的频率作为激振频率。相反，在非共振频率点进行试验，可得到比较准确的质量流量，所以在测量质量流量时应避免共振频率点。通过试验可以证明该结论，见表5。

5　结束语

介绍了直圆柱管科氏质量流量计的数学模型，给出了含流体直圆柱管道的运动方程及其解。通过试验证明了使用该方法获得的质量流量与实际值接近，但存在误差。通过理论和试验分析了产生误差的原因，获得以下结论：

(1)在相同的激振频率和流量作用下，激振力的大小会造成圆柱管内质量流量的测量误差，流量高时的测量误差比流量低时的测量误差小。

(2)在相同激振力和流量作用下，激振频率的大小会影响圆柱管内质量流量的检测精度，通过理论和试验分析可证明该结论正确。当使用非共振频率激振时，试验值与实际值接近，但误差在允许范围内，离共振频率点越远测量误差越小。

(3)在共振频率点激振时，试验值与实际值相差较大且无规律，理论分析可证明试验结论正确。在测量质量流量时，不应使用液体静止和流动时圆柱管的共振频率点。

参考文献：

[1]KANG M G．The influence of rotary inertia of concentrated masses on the natural vibrations of fluid-conveying pipes．Journal of Sound and Vibration，2000，238(1)：179-187．

[2]KUIPER G，，METRIKINE A V．Dynamic stability of a submerged，free hanging riser conveying fluid．Journal of Sound and Vibration，2005，280(3)：1051-1065．

[3]李兵，谢里阳，郭星辉．流体对薄壁圆柱管振动频率的影响．振动与冲击，2010，29(7)：193-195．

[4]樊尚春．非线性对Coriolis质量流量测量管振动特性影响的理论研究．仪器仪表学报，2002，23(4)：361-365．

[5]PAIDOUSSIS M P，LUU T P，LAITIER B E．Dynamics of finite-length tubular beams conveying fluid．Journal of Sound and Vibration，1986，106(2)：311-331．

[6]吴福光，蔡承武，徐兆．振动理论．北京：高等教育出版社，1987．

[7]杨俊，陈明．直管式科氏质量流量计最佳测量点分析．航空计测技术，2003，23(4)：5-8．

[8]汪克文，朱超平，周一届．直管科氏质量流量计传感器理论设计．自动化与仪器仪表，2000(3)：47-49．

[9]李兵，魏玉兰．薄壁直圆柱管质量流量的测量与特性分析．制造业自动化，2013，35(5)：63-66．

[10]倪伟．科里奥利质量流量计的信号处理方法的研究．测试技术，2004(3)：6-9．