中学教师的数学教学认识信念的调查研究

喻 平

(1.南京师范大学 数学科学学院；2.南京师范大学 课程与教学研究所，江苏 南京 210097)

国外关于认识信念的理论研究主要集中在3个方面：个体认识论的发展、个体认识的信念系统、个体认识的元认知过程[1]。在教育领域，出现了大量关于教师认识信念和学生认识信念的研究成果。就教师认识信念的研究来看，学者们更多关注的是教师的认识信念与其教学的关系，教师认识信念对学生认识信念的影响，教师认识信念的发展。

一些研究表明，教师的信念影响他们使用教学策略的类型[2]，教师认识信念是整个课堂的认识氛围的重要组成部分[3]。Marra研究了大学教师的认识信念对建构学习环境的影响，包括教师对教学模式、教学辅导、脚手架搭建等学习支持策略选择的影响[4]。Buehl等研究认为，教师的认识信念对教学设计起着关键性作用，例如，如果一位教师持柏拉图主义数学观或工具主义数学观，他在教学中选用的教学策略就会更多地注重训练技能和强调记忆[5]。Brownlee等对目前关于教师的认识信念同课堂教学和学业成就的研究作了总结。已有研究主要集中讨论了教师的认识信念同教师教学行为的关系，而对教师认识信念如何影响学生学习的探讨不多。主要结论可以概括为：第一，拥有成熟认识信念的教师可能在课堂上更多地解决结构不良问题和强调反思，而与之相反的则是突出基本技能和传输核心概念和事实。第二，拥有成熟认识信念的教师更可能注重使用策略将知识建立为个人意义，并将那些与重要知识有联系的思想系统化[6]。

既然教师的认识信念与教学之间的关系密切，研究的起点就应当从教师到底实际拥有什么样的认识信念开始，综观国内在这方面的研究，理论探讨比较多，对教师认识信念的调查研究则很少。就数学教育而言，课程改革已进行了10年，当下数学教师的教学认识信念是一种什么状况，数学教师对数学学科、教学本质、学习过程的认识持有何种信念？这是一个应当而且必须要研究的问题。本研究通过问卷调查了解中学数学教师的教学认识信念状况。

一、研究设计

(一)概念界定

个体认识信念是一个比较宽泛的概念，它是指个人对知识和知识认识过程的见解和信念。把这一概念的内涵加强，框定在教学领域并进一步限定在数学教学领域，就是数学教师的教学认识信念。

数学教学认识信念主要由两种信念组成：数学认识信念，教学认识信念。数学认识信念指教师对数学本体的认识，教学认识信念指教师对教学与学习本质的认识，两者相互交织形成数学教师特有的认识信念倾向系统[7]。

1.数学认识信念包括4个维度

(1)数学真理性的信念；(2)数学价值性的信念；(3)数学客观性的信念；(4)数学知识结构性的信念。

2.教学认识信念包括9个维度

(1)教学目的信念：教师对教学目的的认识；(2)教学本质的信念：教师对教学本质属性的看法；(3)教学方法信念：教师对数学教学方法的认识；(4)教学操作信念：教师在教学操作中的行为习惯；(5)教学评价信念：教师对评价功能的认识和运用；(6)学习本质的信念：教师对学习本质的理解和认识；(7)学生角色信念：教师对学生在教学过程中的地位的认识；(8)学生学习能力的信念：教师对学生学习能力的认识；(9)影响学生学习因素的信念：教师对影响学习的因素的认识。

(二)研究工具

国外关于教师认识信念的研究主要采用里克特量表以及半结构访谈。Marlene认为，个体认识信念系统至少包括5个维度：(1)知识的来源，知识是从权威那里传承下来的还是通过主观和客观的方法推论出来的；(2)知识确定性，知识是绝对的还是不断进化的；(3)知识的结构，知识是各自独立的还是高度综合互相交织的；(4)学习的能力，学习能力是先天遗传的还是后天通过经历获得的；(5)学习的速度，学习是快速的，还是一个渐变的过程，或者完全学不会。在此基础上，Marlene提出了一种测量个体认识信念的SEQ五维度模型，并制作了SEQ量表[8]。后来大多数研究都直接使用SEQ量表，或者对该量表进行修编后再使用。

国内关于教师认识信念的量表也基本上采用克特量表或半结构访谈，如2000年，俞国良和辛自强研究了教师信念及其对教师培养的意义，修编了Smith(1993)有关教师信念的四点量表，该量表主要从发展和传统两个维度对教师的信念进行测量[9]。黄毅英等对中国内地数学教师关于数学知识的信念作了半结构访谈调查[10]。杨豫晖采取质的研究方法，根据访谈资料，从“本土概念”和“关注的焦点教学因素”切入，检视和反思了小学数学教师教学行为背后“隐含的信念”[11]。此外，国内学者更多的是针对学生认识信念展开研究[12]。

本研究采用一种二维结构[7]的工具。数学认识信念是一个维度，教学认识信念是另一个维度，两者组成一个直角坐标系(见图1)。在教学认识信念轴(横轴)上有5个点坐标X1、X2、0、X4、X5，其中0是坐标原点，5个点分别表示5种认识论：行为主义(X1)、认知主义(X2)、信息加工建构主义(0)、个人建构主义(X4)、社会建构主义(X5)。在数学认识信念轴(纵轴)上有5个点坐标Y1、Y2、0、Y4、Y5，其中0是坐标原点，5个点分别表示5种认识论：二元绝对论(Y1)、多元绝对论(Y2)、分离的相对性绝对论(0)、联系的相对性绝对论(Y4)、相对可误论(Y5)。这个结构反映的是教师认识信念的一种倾向性。

图1 数学教师认识信念倾向性的二维结构

二元绝对论是一种绝对主义知识观，认为世界由简单的二歧性构成，被分为真与假，知识不是理性判断而是由权威确定的，科学知识是绝对真理。多元绝对论也是绝对主义知识观，但认为同一个主题或问题有多种解答、观点或评论，任何人有权持自己的观点，不认同权威。相对绝对论把知识视为真理的载体，但真理取决于知识的内在结构、逻辑、证明，而不是权威的裁定。相对绝对论又分为分离性相对绝对论和联系性相对绝对论。分离性相对绝对论强调客观和规则，注重结构、形式体系与关系、区别、评论、分析和思辨，强调知识的内在逻辑关系、证明以及形式结构，以绝对主义知识观为主要倾向。联系性相对绝对论把绝对主义知识观和相对主义知识观结合起来，强调认识的主体、情感、关怀、同情、环境在知识认知中的作用。虽然联系性相对绝对论视知识为绝对的，但强调认识中个人的作用及个人在理解、掌握和处理问题时的自信心和自主性，明显又带有相对主义知识观色彩。相对可误论持可误主义知识观，认为知识的真理性是相对的，知识是发展的，知识的发展受社会发展的制约，知识应当理解为社会建构，价值应当以社会公正为核心，知识、个体和社会3个方面相互作用、协同发展。二元绝对论、多元绝对论、分离性相对绝对论、联系性相对绝对论、相对可误论是对知识本体认识的5种不同信念，同时也反映了人们认识知识属性的一个历史进程。

以对学习本质的理解为基准，把教师的教学认识信念分为5种类型：行为主义、认知主义、信息加工建构主义、个人建构主义、社会建构主义。按此顺序，反映一条从传统到现代、从客观机械论到相对辩证论的发展路向。

于是，从图1中可知：

1.横轴从左到右有两层涵义

(1)传统教学认识信念到现代教学认识信念的演变；(2)客观主义教学认识信念向相对主义教学认识信念的转变。

2.纵轴从下到上有两层涵义

(1)数学传统认识信念到数学现代认识信念的演变；(2)客观主义数学认识信念向相对主义数学认识信念的转变。

坐标原点0表示信息加工建构主义和分离的相对性绝对论，兼有客观成分和相对成分、传统成分和现代成分，因此，4个象限分别表示不同的含义。第I象限：现代教学信念—相对论数学信念；第II象限：传统教学信念—相对论数学信念；第III象限：传统教学信念—客观论数学信念；第Ⅳ象限：现代教学信念—客观论数学信念。

针对数学认识信念的4个维度和教学认识信念的9个维度，编制13个问题，每个问题由5个陈述句组成，5个陈述分别对应每一个维度，表示对数学的认识信念或教学的认识信念。每一个陈述分别对应认识信念倾向二维结构的一个观点，被试只能在5个陈述中选择一个自己最认可的陈述。根据被试的选择，可以在二维结构坐标图的X轴或Y轴上用一个点表示。被试做完整个问卷后，在横轴上有9个选择结果，纵轴上有4个选择结果，即每个被试在坐标系中有13个选择结果。计分方法如下：

(1)从X1到X5分别赋值2，1，0，1，2；从Y1到Y5分别赋值2，1，0，1，2。

(2)量表测量形式，5个问题一组，要求被试做出唯一选择，5种选择分别对应横轴上的5个点或纵轴上的5个点。于是可以在坐标系中横轴或纵轴上找到一个对应点，用xi(i=1，2…9)或yi(i=1，2，3，4)表示。

(3)在每一象限内，计算∑xi+∑yi，分别得到4个象限的得分S1，S2，S3，S4。

这样就可以计算出每一个被试的分数，从而判断其认识信念倾向。再对全体样本的数据进行统计分析，判断教师群体的数学教学认识信念倾向。

使用量表，对南京市初中“省培”教师63人进行了两次测试，在Ⅰ、Ⅱ、Ⅲ、Ⅳ象限的平均分；第一次依次为10.231、6.815、4.473、8.227；第二次依次为10.412、6.223、4.726、8.451。两次测试分数在4个象限I、II、III、Ⅳ的相关系数分别为：0.67**、0.42**、0.55**、0.61**(**p<0.01)，存在非常显著相关，说明量表有较高的信度。量表的结构效度见表1，4个象限得分的两两相关系数均低于它们分别与总量表的相关系数，说明量表有良好的结构效度。

表1 量表的结构效度分析

注：**p<0.01。

Olafson等人从认识论和本体论两个维度构建了一个二维结构的四象限量表。认识论是研究人们关于知识来源和知识获得的信念，本体论是研究人们对现实自然认识的信念。四象限量表由直角坐标系构成，两条轴分别表示认识论和本体论，从现实主义到相对主义逐渐变化，在4个象限中，一个人能够评价他自己属于现实-现实主义、现实-相对主义、相对-现实主义或相对-相对主义之一，个体能够在4个象限的一个区域内选择一个点来对应他自己关于教学的认识信念和本体世界观[13]。这个二维结构表达的是人们对知识和世界的认识，不涉及教学元素，即不是直接针对教学的本意展开描述，与我们构建的数学教师认识信念倾向性二维结构是有很大差异的。

(三)被试

利用2013年“国家级教师培训计划”各地的集训机会，选择部分省的培训教师作为调查对象(包括初中教师和高中教师)，删除无效问卷后共计362人，其中：河南42人、湖南15人、山西133人、山东24、福建17、浙江47人、江西28人、湖北56人。

(四)数据分析

采用SPSS19.0统计软件，分析全体被试在4个象限得分的差异，从而判断教师的认识倾向；选择样本数较大的河南、山西、浙江、湖北4个省作比较，了解各省中学教师的数学教学认识信念差异。

二、研究结果

(一)中学教师的数学教学认识信念倾向

对全体被试在4个象限的得分进行统计描述，结果见表2。

表2 信念数据整体性描述N

对4个象限的数据进行单因素方差分析，结果见表3。

表3 信念数据的方差分析平方和

对4个象限数据进行多重比较，结果见表4。

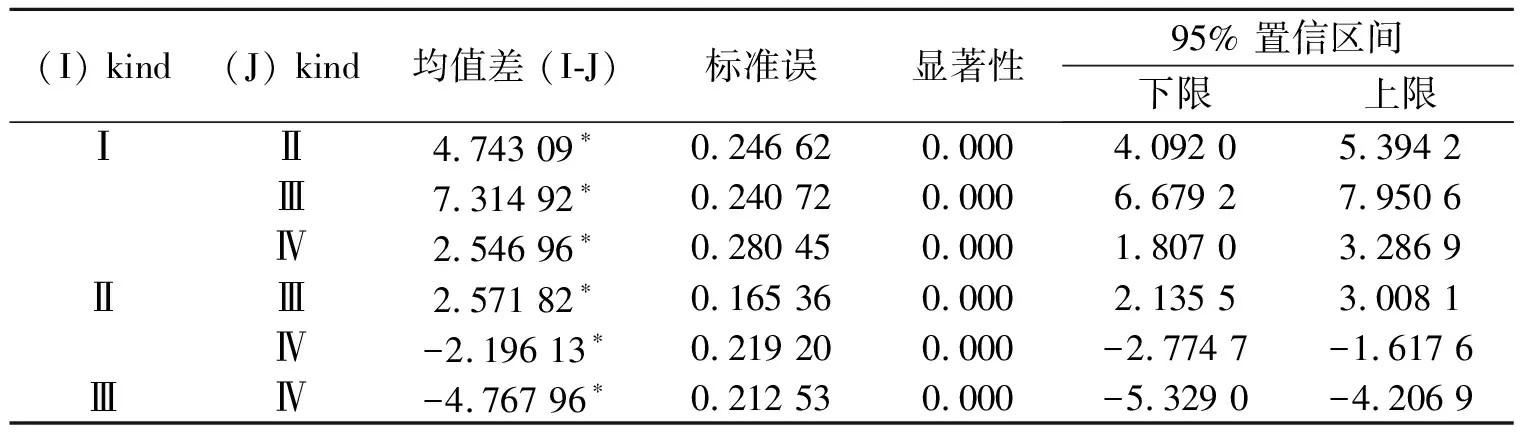
表4 信念数据的多重比较

注：*均值差的显著性水平为 0.05。

表2反映了中学教师的数学教学认识信念的基本情况，得分情况由高到低依次为I、Ⅳ、Ⅱ、Ⅲ，表明教师的教学认识信念倾向由强到弱依次为：现代教学信念—相对论数学信念、现代教学信念—客观论数学信念、传统教学信念—相对论数学信念、传统教学信念—客观论数学信念。由表3和表4可以看到，4个象限得分的差异是非常显著的。因此，就整体来说，中学教师的数学教学认识信念倾向于现代教学观，对数学本体的认识倾向于相对主义。

从选项坐标原点0的情况看(表5)，χ2=7.00，p=0.429>0.05，没有显著性差异。这个结果反映了中学教师近五分之一的倾向是信息加工建构主义和分离的相对性绝对论，即兼有客观成分和相对成分、传统成分和现代成分的观点，而且，各地中学教师的认同度基本是相近的。

表5 选项坐标原点0的数据统计

(二)中学教师数学教学认识信念的地区差异

选择河南、山西、浙江、湖北(编号分别为1、2、3、4)4个省中学教师的数学教学认识信念进行比较，分别对4个象限得分的情况作方差分析。

对第Ⅰ象限的得分作方差分析(表6)，可以看到，4个省教师的数学教学认识信念在第Ⅰ象限中存在差异。再对方差进行齐性检验，发现方差不齐性，故选择Tamhane’s T2进行多重检验(表7)，经过多重比较发现，只有第1组与第4组存在非常显著的差异，其他组之间不存在显著性差异。这一结果说明河南(平均分数为12.7)与湖北(平均分数为10.2)的数学教师对数学教学现代观和数学学科的相对观认同度是不一样的，相对而言，河南教师的认同度高于湖北教师。

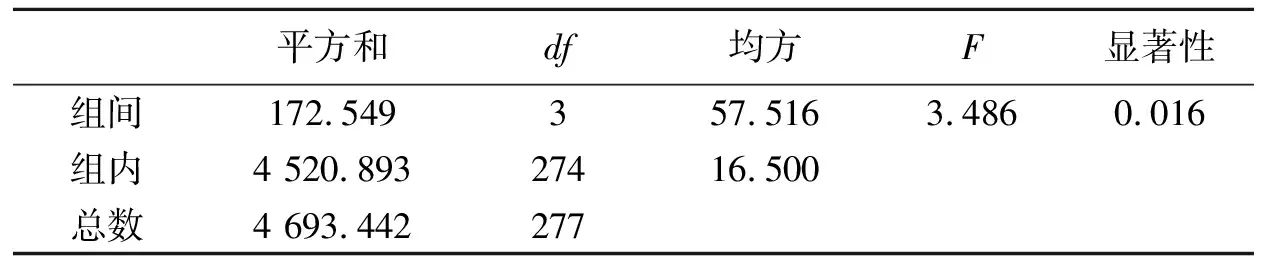
表6 第Ⅰ象限得分的方差分析结果平方和

表7 第Ⅰ象限得分的多重比较

注：*均值差的显著性水平为 0.05。

对第Ⅱ、Ⅲ、Ⅳ象限的得分进行方差分析(方差分析表略)，发现在第Ⅱ象限内，4个省教师的得分没有显著性差异，但是多重比较显示第1组与第2组之间存在显著性差异(表8)；第Ⅲ象限各组之间没有显著性差异，多重比较也不存在显著性差异(表9)；第Ⅳ象限中，方差分析显示各组之间整体存在显著性差异，经过多重比较后可以看到，第1组与第2组、第3组、第4组之间均存在非常显著差异，其余各组之间不存在显著性差异(表10)。

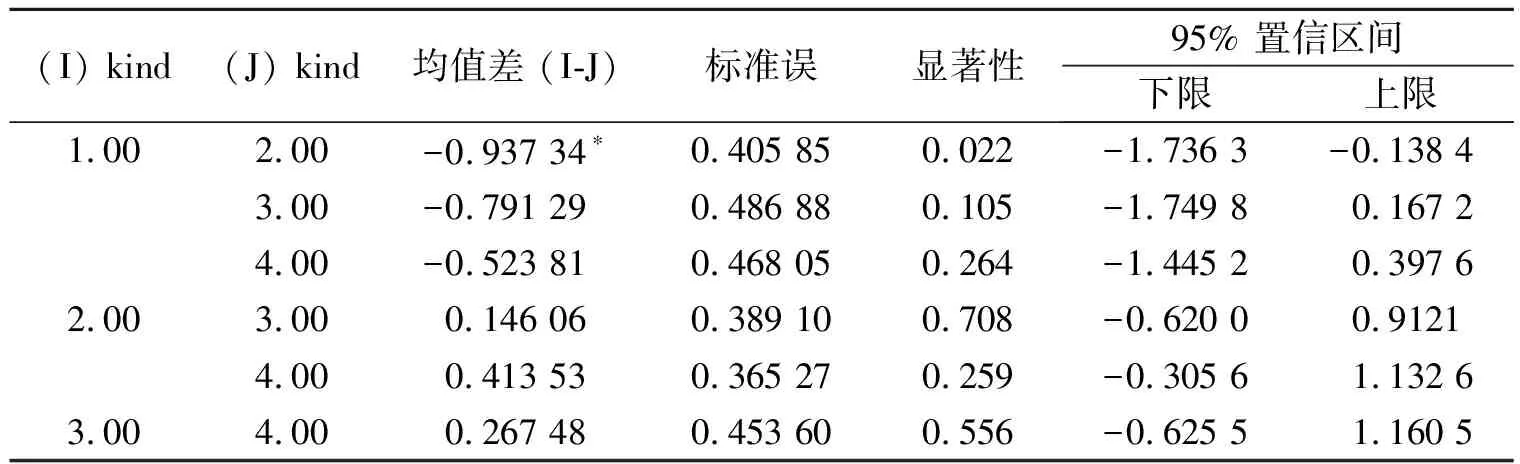
表8 第Ⅱ象限的多重比较

注：*均差值的显著性水平为0.05。

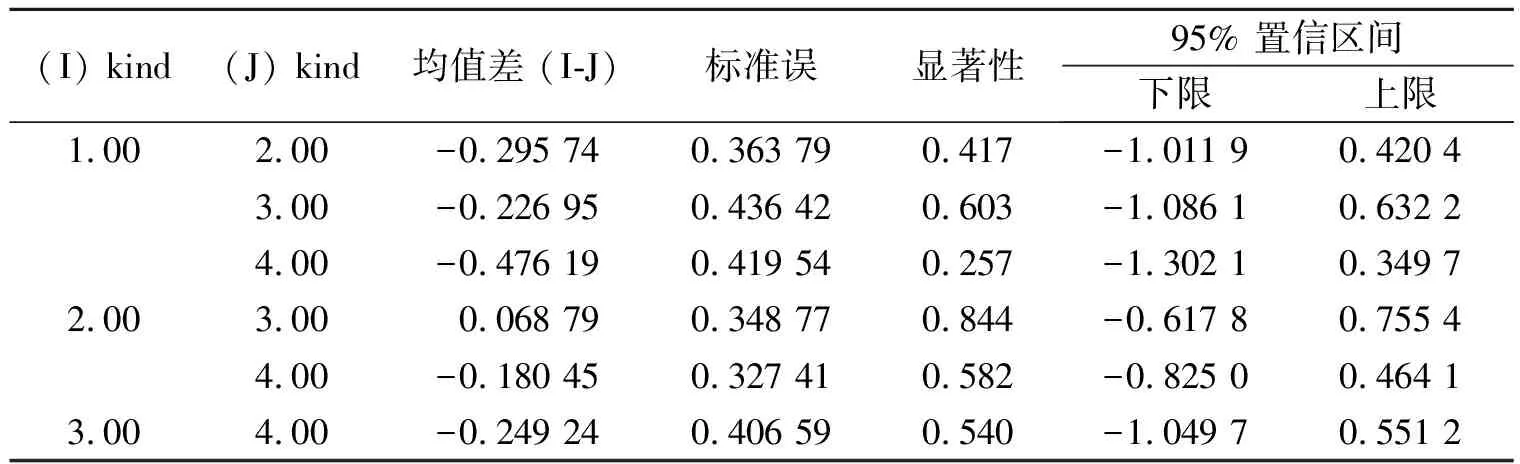
表9 第Ⅲ象限的多重比较

表10 第Ⅳ象限的多重比较

注：*均差值的显著性水平为0.05。

这些结果显示，在“传统教学信念—相对论数学信念”维度上，山西教师的认同度最高，河南教师的认同度最低，两者存在显著性差异，河南、浙江、湖北的教师不存在差异；在“传统教学信念—客观论数学信念”维度上，4个省的教师认同度相近，不存在显著性差异；在“现代教学信念—客观论数学信念”维度上，河南教师的认同度最高，与其他3个省的教师认识信念存在显著性差异，山西、浙江、湖北的教师认同度相近，没有显著性差异。

三、讨 论

(一)总体倾向分析

对全体被试而言，中学教师的数学教学信念倾向依次为：现代教学信念—相对论数学信念、现代教学信念—客观论数学信念、传统教学信念—相对论数学信念、传统教学信念—客观论数学信念。

现代教学信念—相对论数学信念，指个体对教学的认识持有个人建构主义和社会建构主义教学观，对数学的认识持有联系性相对绝对论、相对可误论数学观。个人建构主义认为知识不是个体通过感觉或交流被动接受的，而是由认知主体主动建构起来的，学习是学习者自我建构知识的过程。社会建构主义突出语言、情境、社会等因素在学习中的作用，强调个体的学习是语言、情境、社会互动的建构过程。联系性相对绝对论把绝对主义数学观和相对主义与联系性从优结合起来，强调认识的主体、情感、关怀、同情以及人的因素和周边环境的教育功能。相对可误论数学观认为数学知识的真理性是相对的、动态的、发展的。调查发现“现代教学信念—相对论数学信念”是中学数学教师的主要倾向，而对于第Ⅲ象限“传统教学信念—客观论数学信念”是极少数中学教师认同的，即中学教师们对行为主义和认知主义教学观正在逐步淡化，这一结果反映出在认识上中学教师的观念与课程改革的理念是基本一致的，“现代”逐步冲淡“传统”、“相对”逐步同化“客观”。当然，这与我们选择的被试有关，这些被试是“国培”学员，可能是经过培训后观念更新的结果。

认同度排在第二的是第Ⅳ象限，即“现代教学信念—客观论数学信念”，表示教学信念是现代的，但数学信念是传统的，反映了许多中学教师持有二元绝对论、多元绝对论数学观，即依赖知识由权威仲裁，数学知识是绝对真理，强调技能训练和数学的应用价值，数学知识是静态的，数学教学是知识结果的传递过程。认同度排在第三的是第Ⅱ象限，即“传统教学信念-相对论数学信念”。 第Ⅱ象限表示教学信念是传统的，但数学信念是现代的，传统的教学信念主要是信奉行为主义和认知主义，这两种理论强调知识的客观性，教学目标定位于使学生掌握基础知识，形成基本技能，发展数学能力。第Ⅳ象限和第Ⅱ象限反映的两种倾向本身是有矛盾的，或者在教学观念上认同现代，但在数学观念上认同传统，或者在教学观念上认同传统，而在数学观念上认同现代，这种互为反向的认识信念倾向会造成教师在教学实践中的困惑，形成教学操作上的困难。我们认为，正是有相当中学教师持有“现代教学信念—客观论数学信念”和“传统教学信念—相对论数学信念”，影响到了新课程的实施，同时也是对一些研究发现教师信念与教学行为不一致的一种解释，由于“言”与“言”不一致，造成“言”与“行”不一致。

此外，选项坐标原点0占总选项的18.7%，反映出有相当数量的中学教师持有信息加工建构主义和分离的相对性绝对论信念，即兼有客观成分和相对成分、传统成分和现代成分，各地中学教师在这一点上没有差异，表明是一种共同取向。应当说，这种信念有一定理性色彩，也有适当的辩证性，但有接受现代难弃传统、承认相对难否客观之嫌，对教学实践无疑也会产生不利影响。

黄毅英等调查发现，我国数学教师的数学观主要是柏拉图主义的观点，即把数学看成是静态的永恒不变的学科，它通过逻辑而将知识组织成为一个彼此联系的结构[10]。柏拉图主义的观点就是二元绝对论或多元绝对论，因此，我们的调查结果与黄毅英的结果不完全一致，可能的原因是：其一，研究内容不同，一个研究是只从数学观一个维度切入，另一个研究是从数学观和教学观两个维度切入；其二，研究方法不同，一个是个案访谈式研究(15个被试)，一个是群体调查研究(362个被试)。但是，我们的调查表明有相当数量的中学教师持“现代教学信念—客观论数学信念”倾向，这一点与黄毅英教授的研究结果是基本一致的。

(二)差异倾向分析

第Ⅰ象限：河南与湖北存在差异；第Ⅱ象限：山西与河南存在差异；第Ⅲ象限：4个省之间不存在差异；第Ⅳ象限，河南与其他3个省存在差异。除此之外，其他情形均不存在数学教学认识信念的差异。总体而言，各地中学教师数学教学认识信念差异不大，这是主流。

数学教师认识信念差异的形成，其原因可能是多方面的：第一，各省的文化传统存在差异，包括社会对教育的价值观的认识，家长对小孩的不同期望值，地方行政官员的办学指导思想等都存在不同的认识，从而影响教师的教学认识信念发展；第二，各地教师本身的素质存在差异。教师专业发展一方面依托教师专门机构培训，另一方面依靠教师自我的教学实践反思。目前国内的教师培训非常多，虽然“国培计划”已经有了统一的大纲，但各地在具体实施时仍是随心所欲，造成各地教师培训的内容、方式、评价风格各异，因而对教师素质的提升造成了一种相对的不平衡性。这也反映出一个问题，就是应当对教师培训计划和实施进行系统研究，消除各地教师培训质量的不平衡性。教师在教学实践中的相互交流、协商、沟通和自我反思，形成教学研究共同体，是教师专业发展的有效途径，这是校本教研要研究的问题。

四、结 论

第一，中学教师的数学教学认识信念倾向依次为现代教学信念—相对论数学信念、现代教学信念—客观论数学信念、传统教学信念—相对论数学信念、传统教学信念—客观论数学信念，反映了大多数中学教师的数学教学认识信念与课程改革的理念主流是一致的。

第二，各地中学教师数学教学认识信念有一定差异，但差异不是十分显著。通过规范的教师培训计划，引导教师养成教学反思意识、形成教学研究共同体是完善中学教师数学教学认识信念的有效途径。

致谢：感谢福建师大李袆，杭州师大叶立军，山西师大杨红萍，湖北工程学院李渺，湖南师大谢圣英，河南师大王振平，山东师大于文华为本研究提供调查资料。

参考文献：

[1] 喻平，唐剑岚.个体认识论的研究现状与展望[J].心理科学进展，2007，15(3)：443-450.

[2] Tsai C C. Nested Epistemologies: Science Teachers’ Beliefs of Teaching, Learning and Science[J]. International Journal of Science Education, 2002, 24(8): 771-783.

[3] Muis K R, Bendixen L D,Haerle F C. Domain-generality and Domain-Specificity in Personal Epistemology Research: Philosophical and Empirical Reflections in the Development of a Theoretical Framework[J]. Educational Psychology Review, 2006(18): 3-54.

[4] Marra R. Teacher Beliefs: the Impact of the Design of Constructivist Learning Environments on Instructor Epistemologies[J]. Learning Environments Research,2005(8): 135-155.

[5] Buehl M,Alexander A,Murphy P. Beliefs about Schooled Knowledge: Domain Specific or Domain General[J]. Contemporary Educational Psychology, 2002, 27(3): 415-449.

[6] Brownlee J M, Edwards A, Berthelsen D C, etc. Self-authorship in Child Care Student Teachers[G]//Brownlee J M, Schraw G J,Berthelsen D C. Personal Epistemology and Teacher Education.New York and London:Routledge,2011:68-83.

[7] 喻平.数学教师认识信念的一个理论框架与量表设计[J].数学教育学报，2013，22(4)：34-38.

[8] Marlene S. Effects of Beliefs about the Nature of Knowledge on Comprehension[J]. Journal of Educational Psychology, 1990, 82(3): 498-504.

[9] 俞国良，辛自强.教师信念及其对教师培养的意义[J].教育研究，2000(5)：16-20.

[10] 黄毅英，林智中，黄家鸣，等.中国内地中学教师的数学观[J].课程·教材·教法，2002(1)：68-72.

[11] 杨豫晖.教师教学信念的检视与反思——以小学数学教师为例[J].课程·教材·教法，2010(12)：100-106.

[12] 张侨平，黄毅英，林智中.中国内地数学信念研究的综述[J].数学教育学报，2009，18(6)：16-20.

[13] Olafson L, Schraw G, Veldt M V. Consistency and Development of Teachers’s epistemological and Ontological World Views[J]. Learning Environments Research, 2010(13): 243-266.