目标运动对激光辐照温度场的影响
李小将,张东来,杨业伟
(1.装备学院研究生管理大队,北京101416;2.装备学院激光推进及其应用国家重点实验室,北京101416)
1 引言
国内外对激光辐照物质进行了一系列的理论和实验研究。美国劳伦斯·利弗莫尔国家实验室(Lawrence Livermore National Laboratory,LLNL)的C.D.Boley等[1]利用固态热容激光器进行了辐照金属板、熔融石英等材料的实验,建立了二维热传导模型,将实验数据和数值求解结果进行了对比分析;国防科技大学的焦路光等[2]建立了激光垂直照射金属圆板的辐照模型,并对金属圆板温度场分布进行了数值求解;中国工程物理研究院王伟平等[3]利用重复脉冲激光器辐照圆柱形金属壳体,测量了壳体表面和背面的温度场分布。然而,上述模型和实验中的研究对象都是理想条件或实验室条件下的静止目标。
本文分析运动目标辐照参数特性对激光辐照温度场的影响。首先分析激光辐照运动目标情形下,辐照参数随目标运动的变化,包括平均功率密度、光强分布和对流换热通量;其次,利用有限容积法数值求解激光辐照运动目标的温度场分布;最后,分析辐照参数对温度场分布的影响。
本文研究背景具有比较强的应用性,通过描述激光辐照运动目标温度场分布,以及分析运动目标辐照参数特性对温度场分布的影响,为进一步研究激光对运动目标的辐照效应奠定了基础。
2 激光辐照运动目标参数求解
本文选择地基激光辐照水平匀速运动圆柱体目标为研究背景。作者在文献[4]中建立了激光辐照目标的交汇场景,本文只进行简要说明,如图1所示。

图1 地基激光辐照运动目标交汇场景Fig.1 Encounter scene of ground - based laser irradiatingmoving target
本文对交汇场景做如下设定:
(1)目标水平匀速运动,速率为V0,轴线与轨道重合,高度为恒定值H;
(2)地基激光器位于运动目标的轨道线上,且位于目标运动前方,辐照初始时刻水平距离为D;
(3)运动目标为圆柱体结构,底面半径为R1,长度为d,激光辐照位置为圆柱体的侧面,辐照中心点位于圆柱体侧面可视部分的表面中心;
(4)激光束与水平夹角为变量α;
(5)激光器为连续波氟化氘化学激光器,激光束强度的空间分布为高斯分布;
(6)目标材料为30CrMnSiA钢。
2.1 平均功率密度
传输距离为L,激光光束扩散半径a为:

式中,为光束发散角。
光束发散角受光束衍射发散角、激光光源抖

可以得出,平均功率密度P由发射功率P0、大气衰减系数γ、光束发散角和激光传输距离L确定。在激光辐照过程中,平均功率密度P随着传输距离L的变化而变化。
2.2 光强分布
假定激光束到达运动目标附近,激光束为半径为a的圆柱形光束。激光束强度的空间分布为高斯分布:

式中,I0为激光光斑中心的热源强度,可由平均功率密度q积分求得;r为光斑区域内任意一点到光斑中心的距离;a为激光束的光斑半径;I(r)仅在光斑区域内有定义,其余区域内为0。
激光束到达运动目标几何关系示意如图2所示。动角和大气抖动扩散角的综合影响[5]。其中,光束衍射发散角和激光光源抖动角是由激光器自身参数决定;大气抖动扩散角是由大气条件决定。
由光束扩散半径,可以求得光束横截面面积为:

激光在大气中传输,激光能量会产生损失。定义大气透过率τ来描述激光通过大气后辐照到目标上的功率P和发射功率P0之间的关系:

显然,大气透过率τ与激光传输距离L有关。文献[6]给出了大气透过率τ的求解式:

式中,γ为大气衰减系数,由大气分子吸收系数、大气分子散射系数、大气中气溶胶吸收系数和大气中气溶胶散射系数组成。
至此,可以求出激光束到达运动目标的平均功率密度为:
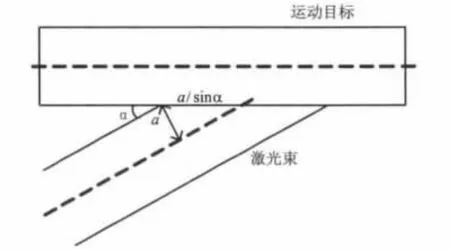
图2 激光束辐照运动目标几何示意图Fig.2 Geometry diagram of laser irradiating flying target
由于激光束与运动目标存在夹角α,激光束在运动目标的截面为椭圆形。其中,椭圆形光束截面的短半轴为a,长半轴为a/sinα。
建立圆柱体目标的三维坐标系O-xyz,激光辐照面域如图3所示。
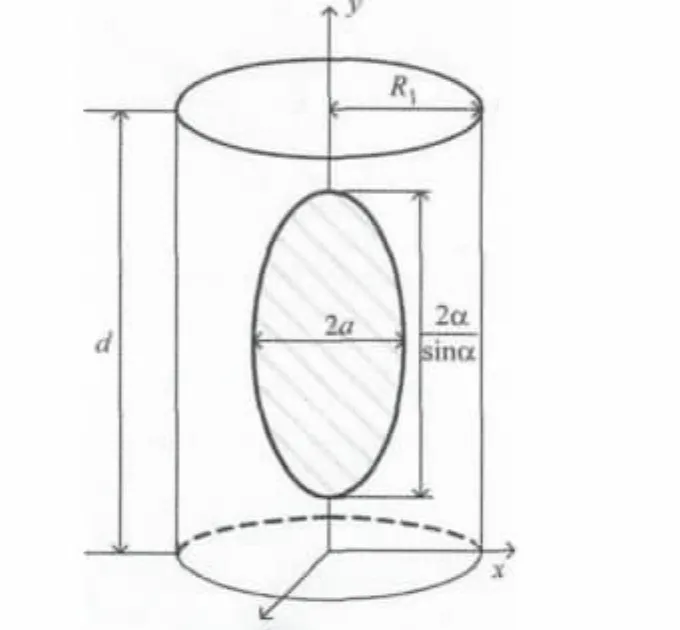
图3 圆柱体目标辐照面域示意图Fig.3 Laser irradiating area of columniform target
相应的激光束强度的空间分布转化为椭圆形高斯分布,光束在x方向上的光束半径rx=a;在y方向上的光束半径ry=a/sinα。激光束强度的空间分布的表达式为:

可以得出,激光束不是垂直辐照运动目标,而是与运动目标存在夹角α,激光束强度的空间分布转化为椭圆形高斯分布;同时,椭圆形高斯分布的长半轴和短半轴随目标的运动不断变化。
2.3 对流换热通量
目标以速率V0在运动的过程中,圆柱面存在速率为V0的切向气流。目标和切向气流之间存在强制对流换热,是一种重要的热传递形式。
气流与靶面间的对流换热通量由牛顿冷却定律来描述[7]:

式中,hf为对流换热系数;TW为靶面温度;Tr为紧贴靶面的气流温度。
对流换热系数hf主要由气流的属性、气流运动速率和圆柱体目标长度确定;紧贴靶面的气流温度Tr主要是由气流静温、气流运动速率、气流恢复系数和气流绝热系数确定;靶面温度TW为激光辐照下运动目标表面温度。本文利用文献[7]给出的hf和Tr的近似表达式进行求解,具体表达式不再赘述。
可以看出,激光辐照运动目标,目标表面存在强制对流换热,对流换热通量受目标运动速率的影响。
综上所述,区别于激光辐照静止目标,激光辐照运动目标辐照参数的特点主要包括:由于激光器与目标之间距离的变化,辐照面的平均功率密度不断变化;由于激光束与目标存在夹角α,激光束强度的空间分布由圆形高斯分布转化成为椭圆形高斯分布,且其长半轴和短半轴不断变化;由于目标以速率V0水平匀速运动,等同于目标表面存在速率为V0的切向气流,存在强制热对流形式的能量交换。
在求解出激光辐照运动目标平均功率密度、光强分布和对流换热通量等辐照参数的基础上,进一步求解激光辐照运动目标温度场分布。
3 激光辐照温度场求解
3.1 温度场求解过程
求解激光辐照运动目标温度场,需要建立描述热量在目标内传递的热传导方程。建立圆柱体目标的三维柱坐标系O-rθz,由傅里叶定律可知,不存在体热源的情形下,柱坐标下三维瞬态热传导方程为[8]:

式中,ρ为材料密度;c为材料的比热容;T为温度;k为材料的热导率;t为时间。
此外,求解热传导方程,需要关于特定问题的初始条件和边界条件。其中,初始条件为激光辐照初始时刻运动目标的温度;边界条件为加载于圆柱体表面的激光热流密度和对流换热通量,分别由式(7)和式(8)求出。
本文基于离散的思想,采用有限容积法求解上述热传导方程。利用有限容积法求解热传导方程的步骤为:将目标进行空间区域离散;将式(9)转化成各个离散点的离散方程;将边界条件经过处理后加入到离散方程;利用迭代法求解离散方程,进行收敛性判断。
3.2 仿真案例
设定交汇场景参数、激光器参数和运动目标参数,求解激光辐照参数和运动目标温度场分布。
仿真参数设定如表1所示。间分布不断变化。图6给出激光辐照初始时刻t=0 s和激光辐照终止时刻t=5 s激光束强度空间分布。
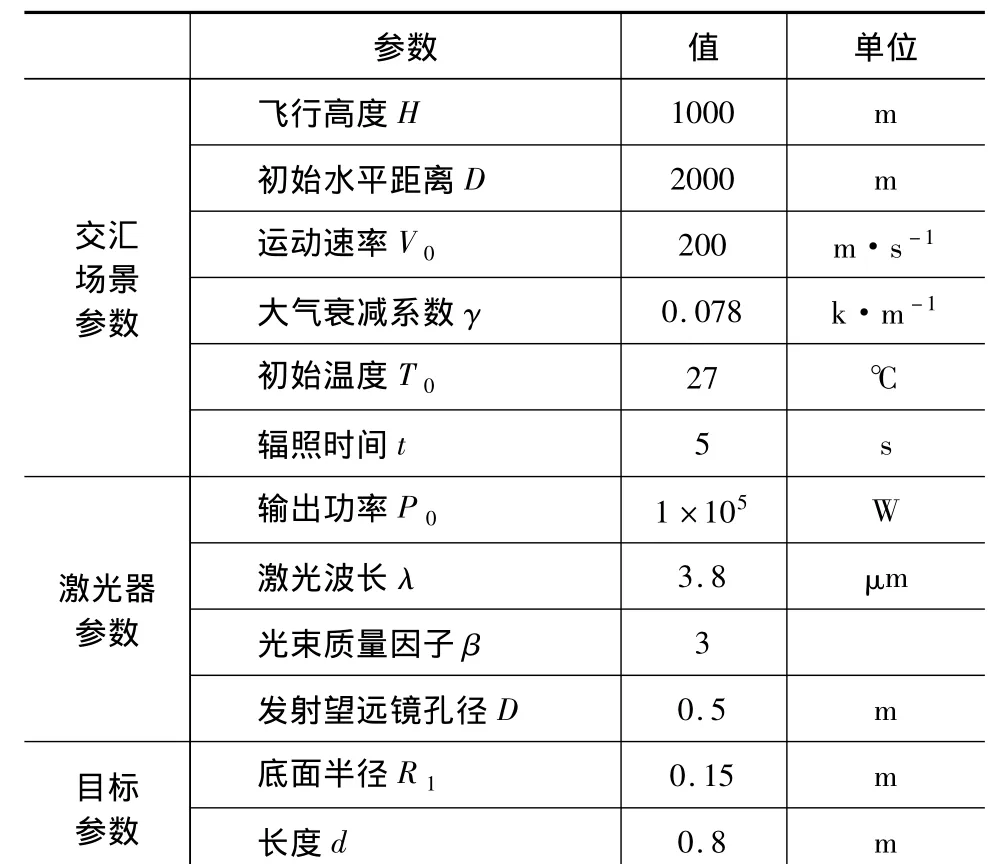
表1 仿真参数Tab.1 Simulation parameters

图5 不同时刻平均功率密度的值Fig.5 Values of average power density at different time

图6 不同时刻辐照面功率密度分布Fig.6 Power destiny distributing at different time
首先求解激光垂直辐照远场静止目标温度场分布。在此场景下,目标辐照参数的特点为:目标辐照面域内平均功率密度为定值;光束强度空间分布为圆形高斯分布;目标表面不存在强制热对流的能量交换。利用有限容积法,求解出目标所有节点在任意时刻的温度值。t=5 s时刻,激光器对圆柱面的可视部分,即半个圆柱面的温度场如图4所示。

图4 圆柱面温度场(t=5 s,静止目标)Fig.4 Temperature field of column area at t=5 s as stationary target
由图4可知,激光辐照静止目标,圆柱面最高温度为268.59℃,位于激光辐照中心点。
求解激光辐照运动目标温度场分布,首先求解激光辐照参数。随目标的运动,平均功率密度随时间的变化如图5所示。
由图5可知,激光辐照运动目标,激光到达目标的平均功率密度是不断变化的。在本文建立的交汇场景和仿真参数下,平均功率密度不断增加。其中,t=0 s,平均功率密度为 501.07 W/cm2;t=5 s,平均功率密度为1335.62 W/cm2。
随目标的运动,由于平均功率密度、光束扩散半径在不断变化,激光光斑中心的热源强度I0、长半轴和短半轴也在随目标运动变化,即激光束强度空
由图6可知,激光辐照运动目标,激光束强度空间分布不断变化:激光光斑中心的热源强度不断增加;椭圆形高斯光束的长半轴和短半轴不断减小;辐照面积不断减小,能量趋于集中。
通过确定气流属性以及运动目标参数,进一步求得目标圆柱面强制热对流的对流换热系数hf值为821.42 W/(m2·K),紧贴靶面气流温度Tr值为34.5 ℃。
利用有限容积法,经过数值模拟,可以求解出目标所有节点在任意时刻的温度值。t=5 s时刻,激光器对圆柱面的可视部分,即半个圆柱面的温度场如图7所示。
图7 圆柱面温度场(t=5 s)Fig.7 Temperature field of column area at t=5 s
由圆柱面温度场分布可以看出,激光辐照区域温升较高;最高温度为652.50℃,位于激光辐照中心点。
4 辐照参数对温度场分布的影响
在温度场求解结果的基础上,对比于激光辐照静止目标,分析运动目标辐照参数特性对温度场分布的影响。其中,包括平均功率密度随时间的变化、激光束强度的空间分布、强制热对流对温度场分布的影响。
4.1 平均功率密度变化影响分析
其他条件不变,不考虑激光辐照过程中平均功率密度随时间的变化,求解运动目标温度场分布。假定激光辐照目标平均功率密度q为恒值,取激光辐照初始时刻值,即501.07 W/cm2。可以求得,激光光斑中心的热源强度I0为1158.80 W/cm2。
利用有限容积法,求解出目标所有节点在任意时刻的温度值。t=5 s时刻,激光器对圆柱面的可视部分,即半个圆柱面的温度场如图8所示。
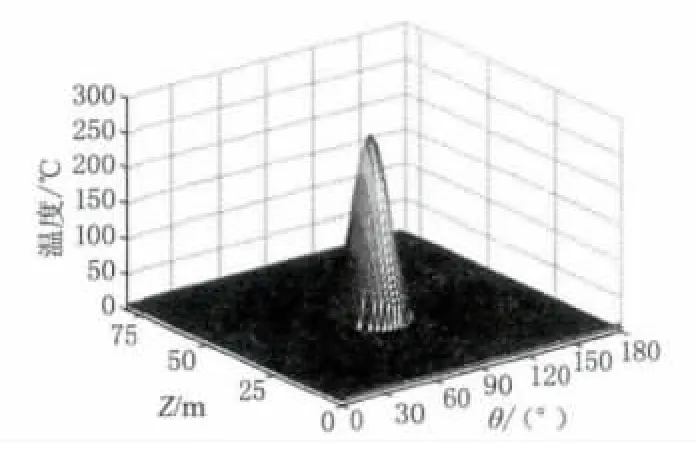
图8 圆柱面温度场(t=5 s,q恒定)Fig.8 Temperature field of column area at t=5 s as q be a constant value
由图8可知,不考虑平均功率密度随时间的变化,圆柱面最高温度为259.35℃,位于激光辐照中心点。比较图7,考虑平均功率密度的变化,辐照面域温度值较高,激光辐照面积没有变化。
上述现象产生的主要原因为:随着目标的运动,由于激光器与目标的距离减小,所以辐照面积不断减小以及能量大气传输损失不断降低,导致辐照面域平均功率密度不断增加,激光辐照引起的目标温升速率不断增加。分析结果表明:平均功率密度随目标运动的变化对温度场分布有很大的影响,求解激光辐照运动目标温度场需要考虑平均功率密度随目标运动的变化。
4.2 光束强度空间分布影响分析
其他条件不变,不考虑激光光束与运动目标的夹角,求解运动目标温度场分布。假定激光光束垂直辐照运动目标,则辐照面域光束强度的空间分布为辐照半径随目标运动不断变化的圆形高斯分布。
利用有限容积法,求解出目标所有节点在任意时刻的温度值。t=5 s时刻,激光器对圆柱面的可视部分,即半个圆柱面的温度场如图9所示。

图9 圆柱面温度场(t=5 s,圆形高斯分布)Fig.9 Temperature field of column area at t=5 s as circular Gaussian beam
由图9可知,不考虑激光光束与运动目标的夹角,圆柱面最高温度为651.60℃,位于激光辐照中心点。比较图7,可以得出,不考虑激光光束与运动目标的夹角,激光辐照面域光束强度空间分布由椭圆形高斯分布转化成圆形高斯分布,辐照面域有较大差异;最高点温度都位于激光辐照中心点,最高温度值几乎相等。
上述现象产生的主要原因为:激光束辐照运动目标的角度不同,辐照面域的光束强度空间分布不同;光束强度空间分布不同,辐照面域不同,温升区域也就不同;由于两种情形下,激光光斑中心热源强度I0相同,则得出激光辐照中心点温度相同。分析结果表明:辐照面域光束强度空间分布对温度场分布有很大的影响,求解激光辐照运动目标温度场需要考虑激光光束与运动目标的夹角。
4.3 热对流影响分析
其他条件不变,不考虑边界强制热对流的影响,求解运动目标温度场分布。
利用有限容积法,求解出目标所有节点在任意时刻的温度值。t=5 s时刻,激光器对圆柱面的可视部分,即半个圆柱面的温度场如图10所示。
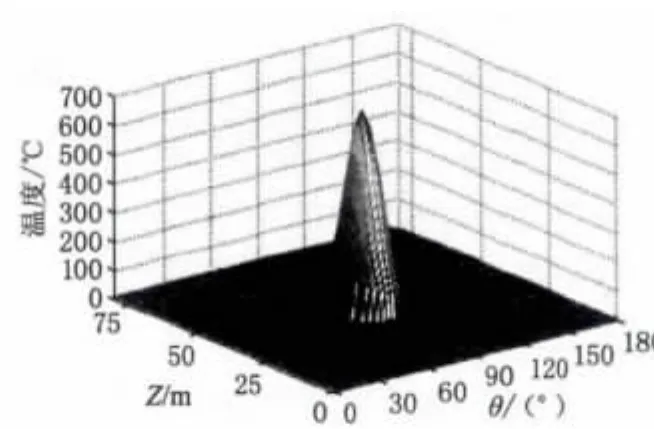
图10 圆柱面温度场(t=5 s,无热对流)Fig.10 Temperature field of column area at t=5 s as no heat convection
由图10可知,不考虑强制热对流的影响,圆柱面最高温度为678.28℃,位于激光辐照中心点。比较图7,考虑强制热对流的影响,目标圆柱面温度值降低,t=5 s时刻,辐照中心点温度值比不考虑热对流影响条件下低25.78℃;激光辐照面积没有变化。
上述现象产生的主要原因为:在激光辐照过程中,考虑强制热对流的影响,存在目标表面与外界环境的能量交换,使得目标表面的温度降低。分析结果表明:运动目标表面强制热对流能量交换对温度场分布有很大的影响,求解激光辐照运动目标温度场需要考虑目标表面存在的强制热对流。
5 结论
本文通过建立激光辐照运动目标的交汇场景,求解平均功率密度、光强分布和对流换热通量等辐照参数,进而求解出目标温度场分布,重点分析了运动目标辐照参数特性对温度场分布的影响,得出如下结论:
(1)随着目标的运动,激光辐照平均功率密度不断增加,目标温升速率不断增加;
(2)激光束辐照运动目标的角度不同,辐照面域的光束强度空间分布不同,温升区域也不相同;
(3)运动目标表面存在强制热对流形式的能量交换,减缓了表面温升。
本文的研究结果对实际工程应用中激光辐照运动目标的建模、温度场求解及参数影响分析提供了一定的思路和方法。
[1] C D Boley,K P Cutter,SN Fochs,et al.Interaction of a high - power laser beam withmetal sheets[R].Llnl- Jrnl-414640,2009.
[2] JIAO Luguang,ZHAO Guomin,CHEN Minsun.Modeling of temperature rise of steel plate irradiated by laser[J].Laser Journal,2010,31(1):25 -27.(in Chinese)焦路光,赵国民,陈敏孙.激光辐照下金属圆板温升的数值模拟研究[J].激光杂志,2010,31(1):25-27.
[3] WANGWeiping,TANG Xiaosong,GUI Yuanzhen,et al.Laser thermal effects on ratatingmetal shell[J].Applied Laser,2001,21(5):319 -321.(in Chinese)王伟平,唐小松,桂元珍,等.激光对旋转金属壳的加热研究[J].应用激光,2001,21(5):319 -321.
[4] ZHANG Donglai,LIXiaojiang,HUANG Yong,etal.Analysis of damage effect of US army ground-based laser against cruise missile[J].Modern Defense Technology,2013,41(6):9 -15.(in Chinese)张东来,李小将,黄勇,等.美军地基激光反巡航导弹毁伤效应分析[J].现代防御技术,2013,41(6):9-15.
[5] LIHaiyan,HU Yunan,LIU Xudong.Energy estimation method for laser disturbing photoelectrical detectors in remote distance[J].Infrared and Laser Engineering,2010,39(6):1038 -1043.(in Chinese)李海燕,胡云安,刘旭东.激光干扰远场光电探测器能量估算方法[J].红外与激光工程,2010,39(6):1038-1043.
[6] HONG Yanji.Physics in direct energy technilogy[M].Beijing:National Defense Industry Press,2011:158.(in Chinese)洪延姬.定向能技术中的物理学[M].北京:国防工业出版社,2011:158.
[7] CHEN Minsun,JIANGManhou,LIU Zejin.Effect of tangential airflow on resin composite irradiated by laser[J].High Power Laser and Particle Beans,2010,22(12):2848 -2852.(in Chinese)陈敏孙,江厚满,刘泽金.切向气流对激光辐照树脂基复合材料的影响[J].强激光与粒子束,2010,22(12):2848-2852.
[8] JPHolman.Heat transfer[M].10th ed.New York:McGraw - Hill Book company,2010.
——目镜套筒

