基于遗传算法随车起重机折叠臂架铰点位置优化

李纯金，褚月桥，周海波

(江苏科技大学机械工程学院，江苏镇江212003)

随车起重机折叠臂架大多采用液压缸控制实现装载、改变工作幅角，从而扩大作业范围，提高工作效率［1］.由于折叠臂架连杆变幅机构有多种组合方式［1］，不同的组合方式液压缸铰点布局不同，导致液压缸受力不同，以及在整个变幅过程中所受力的变化趋势不同，对液压缸的性能、使用寿命、稳定性及工作装置整体性、安全性有较大影响.因此在设计特定的折叠臂架结构时，研究合理的液压缸铰点位置是十分必要的.

目前国内针对铰点位置的优化有了一定的研究，文献［2］利用共轭梯度法，对登高平台消防车起升臂架铰点位置进行优化，降低了变幅过程中油缸受力峰值;文献［3］借助软件Prodopt，采用仿生物进化算法对装载机正转八连杆机构工作装置进行铰点位置优化，经过优化，不但满足了用户对产品性能指标要求，而且还大大提高了产品整体综合工作性能;文献［4］在ADAMS中建立参数化伸缩臂叉车模型，利用设计研究及试验设计功能对连杆变幅机构进行参数化分析，找到最优铰点位置，使得液压缸最大受力减小，实现了优化目标.文中主要以中型随车起重机上的常用折叠臂架结构为研究对象，两液压缸共同作用的折叠臂结构形式，通过建立数学模型，利用MATLAB求解，借助遗传算法全局寻找最优解的能力，得出折叠臂架最优的铰点位置，达到优化的目的.

1 铰点优化数学模型

随车起重机折叠臂架工作装置示意如图1，它是由回转立柱(基础臂)、一级臂(主折叠臂)、二级臂(次折叠臂)、变幅液压缸组成的串联连杆机构.根据随车起重机工作原理分析，随车起重机在变幅起升过程中，各铰点处是薄弱环节，因此对各个铰点受力情况的考察是力学分析中的主要内容，由于随车起重机起升或下降过程速度平缓，故忽略惯性力的影响，只对该过程进行静力学分析.文中着重分析次折叠臂从折叠至打开，随之主折叠臂打开这一过程.由于变幅油缸、各个连杆以及吊钩占机构总质量比例较小，受力分析时可忽略其质量.

图1 随车起重机折叠臂工作装置示意图Fig.1 Diagrammatic sketch of lorry crane working device

1.1 目标函数建立

1.1.1 静力学数学模型

如图2，以二级臂及2号液压缸为分析对象，利用正交分解法建立静力学平衡方程:

上式满足3个未知力，3个方程通过MATLAB求解线性方程组得F2，FGx，FGy.

如图3，以一、二级折叠臂整体为分析对象，利用正交分解法建立静力学平衡方程:

根据上式得转矩M.

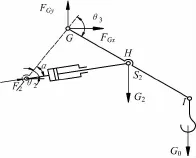
图2 二级折叠臂受力分析Fig.2 Analysis of force graph for second folding jib

图3 整体受力分析Fig.3 Analysis of force graph for the wholemechanism

图4，5，以基础臂和折叠臂整体为分析对象，利用正交分解法建立静力学平衡方程:

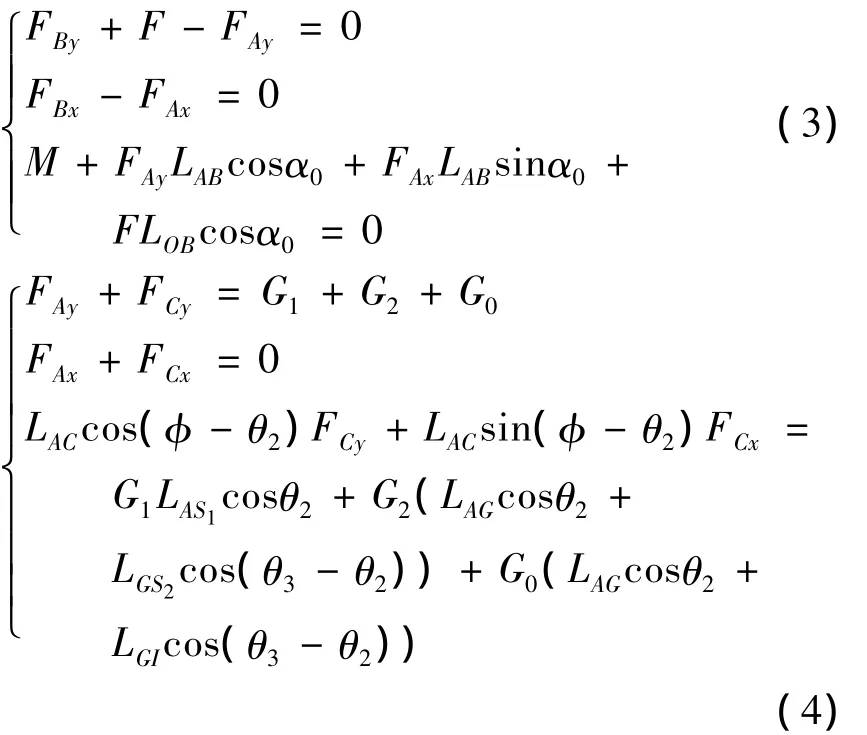
根据式(3，4)通过求解线性方程组得FAx，FAy，FBx，FBy，FCx，FCy.

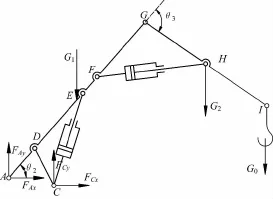
图4 折叠臂受力分析Fig.4 Analysis of force graph for folding jib

图5 基础臂受力分析Fig.5 Analysis of force graph for OA-rod

如图6～8，分别以1号液压缸、连杆CD、主次折叠臂整体为分析对象，利用正交分解法建立静力学平衡方程:

根据式(5～7)联立求解线性方程组得FDx，FDy，FEx，FEy，进而求得F1.

图6 液压缸1的受力分析Fig.6 Analysis of force graph for hydraulic cylinder

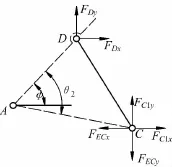
图7 连杆CD受力分析Fig.7 Analysis of force graph for CD－connecting rod

图8 一二级折叠臂整体受力分析Fig.8 Analysis of force graph for folding jib

1.1.2 目标函数的确立

在满足折叠臂架变幅角度和起重负载要求的前提下，为了使变幅过程中液压缸受力趋势变平缓，运行过程更加平稳、安全.根据上述理论计算可知，在θ2，θ3角度变化过程中，1号液压缸受力曲线呈现由高到低的变化趋势，2号液压缸受力曲线呈现由低到高的变化趋势，选取液压缸最大受力Fbf(即液压缸1受力和液压缸2受力)最小为目标函数.依据上述静力学分析结果得目标函数为:

1.2 设计变量的选取

设计变量是设计过程用来调整和优化的独立变量，设计变量选取得越多越能得出更为有利的结果，但是同时这样会增加计算难度，为了得到合理的折叠臂铰点位置，在满足实际要求的情况下，根据静力学分析结果，1号液压缸和2号液压缸受力是由8个独立设计参数决定，因此，选取8个尺寸作为设计变量，即LGF，LGH，LAB.该设计变量可以表达目标函数并且涵盖了需要优化的参数.

X=［LGFLGHLABLBCLCDLDALDELAO］T

1.3 约束条件的确定

1.3.1 边界约束

边界约束可以缩小寻优范围，考虑折叠臂机构尺寸的要求，使得边界约束与总体尺寸参数相互匹配，满足设计要求范围，可给出变量适当的下限和上限，由此建立8个边界约束

ximin≤xi≤ximax(i=1，2，……，8)

式中:ximin，ximax分别为连杆机构设计变量xi的上下限.

1.3.2 性能约束

为了保证油缸的稳定性、制作、安装要求，通常会考虑液压油缸的伸缩比，油缸的伸缩比通常需要满足:

2 铰点优化模型的遗传算法实现

随车起重机折叠臂连杆机构铰点位置较多，设计变量较多，然而多变量优化设计问题是一般传统设计方法难以求解的问题之一［5－6］，但是近年来随着对现代优化设计理论研究水平的提高，粒子群算法、正交算法、遗传算法等智能算法［7－8］的出现，为连杆变幅机构的优化设计提供了新的手段.

2.1 遗传算法原理

遗传算法从称为“初始种群”的一组初始解开始搜寻寻优过程，群体中的每个个体就是问题的一个解.通过选择运算，将适应度较高的个体遗传到下一代;再通过交叉、变异遗传运算产生适应度较高的个体，得到下一代新群体.反复迭代，使群体一代代进化，逐步接近搜索空间的最优解［9］.

2.2 遗传算法求解过程

1 )个体编码.遗传算法不能直接处理解空间的数据，必须通过编码将它们表示成遗传空间的基因型个体符号串.文中采用二进制编码的方式，利用crtbp函数建立二进制种群，将设计变量编码为二进制整数符号串，再通过bs2rv函数实现二进制代码和实值之间的变换.

2 )初始种群.遗传算法是对群体进行操作，所以需要准备一些起始搜索的初始群体，随机产生N个字符串，每个字符串代表一个个体.文中为了保证足够的可行解，设定初始种群规模大小为NIND=100，即群体是由100个个体组成.前两步实现方法为Chrom=crtbp(NIND，NVAR*PRECI)，v= bs2rv(Chrom，FieldD).

3 )计算适应值.适应度函数是用来表示个体或解的优劣性，从而决定遗传机会的多少，对不同的问题，其适应度函数的方式各不相同.由ranking函数分配适应度值，FitV=ranking(ObjV).

4 )选择.对子代和父代共2N个个体进行适应性排序，选择出排在前面的N个个体，选择的准则就是各自的适应度，利用轮盘赌选择法，由Select高级函数实现.SelCh=Select(‘sus’，Chrom，FitnV，GGAP).

5 )交叉.交叉是产生新个体的主要操作过程，将选出的N个个体两两杂交，产生N个新的子代个体.文中设定交叉概率Pc=0.7，通过Recombin函数实现交叉运算.SelCh=Recombin(‘xovsp’，SelCh，0.9).

6 )变异.对新生成种群中每一个个体，以某种概率(称为变异概率Pm)改变某一个或某些染色体上的基因值，为了维持种群多样性，防止丢失一些有用的遗传基因.文中设定变异概率Pm=0.0017，利用离散变异算子mut实现变异运算.SelCh=mut(SelCh，0.0017).

3 实例应用及结果分析

利用文中优化设计方法和程序，针对某型7T随车起重机折叠臂架铰点位置进行优化设计.设定参数如下:LGF=800mm，LGH=1 000mm，LAB=195 mm，LBC=334mm，LCD=375mm，LDA=275mm，LDE=850mm，LAO=951mm.优化前后结果见表1.

表1 优化前后参数值Tab le 1 Contrast between optimal and original

将优化后参数代入折叠臂机构中，即得到优化模型.对该模型利用上述求解方法进行求解，即可得到优化目标函数值及其优化后的曲线，利用MATLAB数据处理和绘图功能，绘制优化前后对比曲线图如图9～18(注意图中标识负号表方向，图中θ2表示一级臂架变幅角度，θ3表示二级臂架变幅角度).

图9 液压缸优化前后受力对比Fig.9 Force contrast between optim ization and initialmodel for 1 hydrau lic cylinder

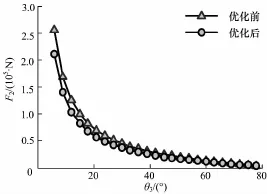
图10 2液压缸优化前后受力对比Fig.1 0 Force contrast between optim ization and initialm odel for 2 hydraulic cylinder

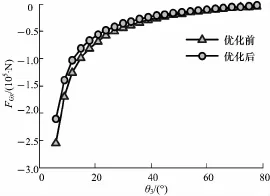
图11 G铰点x向优化前后受力对比Fig.1 1 Force contrast between optim ization and initialmodel for x-axis of hinge G

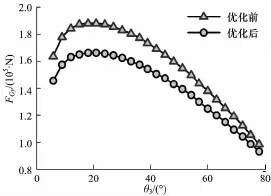
图12 G铰点y向优化前后受力对比Fig.1 2 Force contrast between optim ization and initialmodel for y-axis of hinge G

图13 A铰点x向优化前后受力对比Fig.1 3 Force contrast between optim ization and initialmodel for x-axis of hinge A

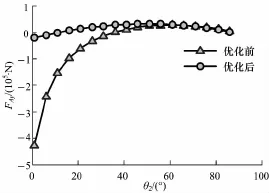
图14 A铰点y向优化前后受力对比Fig.1 4 Force contrast between optim ization and initialmodel for y-axis of hinge A

图15 B铰点x向优化前后受力对比Fig.1 5 Force contrast between optim ization and initialmodel for x-axis of hinge B

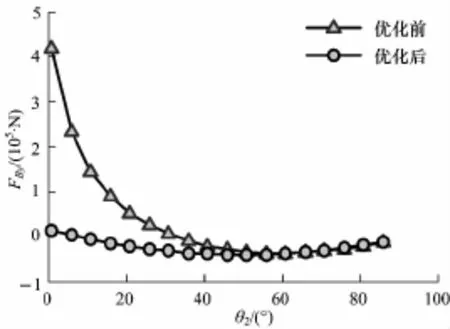
图16 B铰点y向优化前后受力对比Fig.1 6 Force contrast between optim ization and initialmodel for y-axis of hinge B

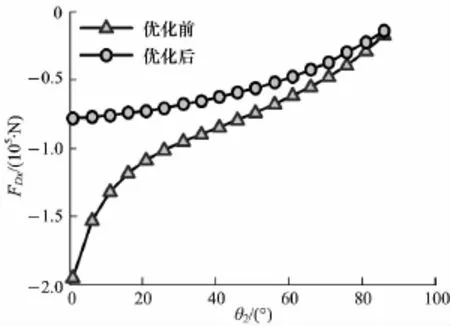
图17 D铰点x向优化前后受力对比Fig.1 7 Force contrast between optim ization and initialmodel for x-axis of hinge D

从结果曲线对比图中发现，液压缸1和液压缸2优化后受力曲线较优化前受力曲线趋势变得更加平缓(图9，10)，尤其是1号液压缸的平缓趋势更为明显，与此同时，新的优化参数对于改善其它铰点的位置受力同样起到了很大的作用，从图11～18中发现，铰点G，A，B，D处在整个过程中较优化前更加趋于水平.

图18 D铰点y向优化前后受力对比Fig.1 8 Force contrast between optim ization and initialmodel for y-axis of hinge D

为了更加精确表达优化后的目标函数值的改善情况，列出了优化前后A，B，D，G及两液压缸受力最大值对比表(表2).

表2 各铰点受力峰值优化前后对照Tab le2 Each hinge force peak between optimal and original (105 N)

从上表中可以清楚地看到，液压缸1和2在启动变幅过程中受力最大值明显降低，分别较优化前降低了9.4%和72.2%，达到了优化的目的.与此同时其余铰点G，A，B，D处受力最大值也不同程度地降低，并且效果很明显，这样对于铰点处的薄弱环节起到了保护的作用.

4 结论

文中通过对目前在中型随车起重机中应用较为广泛的403300型折叠臂架结构进行力学分析，建立了数学模型，并利用遗传算法对该结构进行铰点优化设计，给出了具体的优化过程，从优化结果来看可以得出如下结论:

1 )在满足工作要求的情况下，利用优化后的铰点位置，可以降低液压缸1和液压缸2在工作过程中所受力的最大值，与此同时也降低了其它铰点处所受力的最大值，这样降低了对液压缸受力要求，对其安全性和稳定性方面具有重要的应用价值.

2 )优化后液压缸1和液压缸2在整个工作过程中，受力曲线较优化前变得平缓，即液压系统压力更趋于稳定，液压油波动情况减弱;同时各个铰点在该过程中所受到力的曲线变得平缓，受力趋于稳定，这样有益于改善液压缸的工作环境，增加液压缸的使用寿命，对臂架的稳定性具有重要意义.该设计方法对随车起重机的改进有参照作用，对同类结构的机械设备具有参考价值.

3 )在实际问题中，随车起重机折叠臂架铰点位置确定时，还需考虑臂架刚度、臂架结构形状尺寸要求、自身结构限制以及局部加强筋等因素对铰点布局的影响.文中只针对主要影响因素进行分析，忽略了次要因素，但为了更接近实际模型，优化模型有待进一步提高和完善.

References)

［1］ 姚婧辉.随车起重机变幅机构的仿真分析［D］.辽宁大连:大连理工大学，2009:7－10.

［2］ 潘双夏，刘慧斌，冯培恩.装载机正转八连杆工装装置优化设计［J］.同济大学学报:自然科学版，2001，29(12):549－552.

Pan Shuangxia，Liu Huibin，Feng Peien.Optimization design of 8-bar linkage working mechanism of wheel loaders［J］.Journal of Tongji University:Natural Science Edition，2001，29(12):549－552.(in Chinese)

［3］ 王鑫，滕儒民，高顺德，等.68m登高平台消防车折叠臂变幅机构优化设计［J］.起重运输机械，2008，22 (7):55－57.

Wang Xin，Teng Rumin，Gao Shunde，etal.Optimization design for variable angle mechanism of aerial platform fire truck［J］.Lifting and Conveying Machinery，2008，22(7):55－57.(in Chinese)

［4］ 侯忠明，王胜军，辛涛.基于ADAMS的伸缩臂叉车铰点位置优化设计［J］.起重运输机械，2009，23(6):42－44.

Hou Zhongming，Wang Shengjun，Xin Tao.Optimization of the hinge pointposition of telescopic handler based on ADAMS［J］.Lifting and Conveying Machinery，2009，23 (6):42－44(in Chinese)

［5］ Yang Wei，Wang Jiaxu.Investigation on experimental sensitivity ofwork device natural frequency of hydraulic excavator［J］.Tra-nsactions of the Chinese Society of Agricultural Machinery，2006，37(2):21－24.

［6］ Han Jun，Chen Gaojie.Mechanical property analysis of four－freedom excavation device［J］.Journal of PLAU-niversity of Science and Technology，2010，11(3):290－295.

［7］ 蒋炎坤，刘刚强，李宗，等.基于遗传算法的挖掘机工作装置铰点位置优化［J］.华中科技大学学报:自然科学版，2011，39(3):22－25.

Jiang Yankun，Liu Gangqiang，Li Zong，et al.Optimization of hinge position for working device of excavators by genetic algorithm［J］.Journal of Huazhong University of Science and Technology:Natural Science Edition，2011，39(3):22－25.(in Chinese)

［8］ 刘道华，原思聪，邬长安，等.面向对象的改进遗传算法优化设计［J］.华中科技大学学报:自然科学版，2008，36(7):89－92.

Liu Daohua，Yuan Sicong，Wu Changan，etal.Optimization design of object-oriented and improved genetic Algorithm［J］.Journal of Huazhong University of Science and Technology:Natural Science Edition，2008，36(7): 89－92.(in Chinese)

［9］ 刘建峰，张小辉，蒋志勇，等.基于遗传算法入库钢板分配策略研究［J］.江苏科技大学学报:自然科学版，2011，25(6):524－529.

Liu Jianfeng，Zhang Xiaohui，Jiang Zhiyong，et al.Allocation strategy of steel plate in store house based on genetic algorithm［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2011，25 (6):524－529.(in Chinese)