基于PCA和DEA的江苏省物流业碳排放效率评价

杨 斌，白雪微，白丽莎

(上海海事大学物流研究中心，上海201306)

发展低碳经济已经成为当前的全球性共识.据统计，中国已超过美国成为世界上最大的二氧化碳排放国［1］.因此，无论是从节能减排与社会可持续发展的全球化大趋势，还是从推动经济增长方式转变的国内要求，中国的节能减排均面临巨大的压力与动力.而对于直接影响经济发展的物流业来说，进行物流活动的同时也会产生很多的二氧化碳，对环境造成很大的影响.因此，对地区物流业碳排放效率进行评价与分析有很重要的意义.

国内外已有大量学者研究碳排放效率问题.文献［2］提出了碳指数(单位能源消费的碳排放)作为发展中国家应对气候变化及经济发展模式评价的主要标准;文献［3］将能源强度(单位GDP能耗)作为碳指数来研究气候变化;文献［4］则认为碳排放强度(单位GDP二氧化碳排放量)是评价一个国家或地区碳减排效果的理想指标.随着数据包络分析(data envelopment analysis，DEA)方法应用领域的逐渐扩大，国内越来越多的学者将该方法应用于能源环境领域来研究碳排放效率.文献［5］基于DEA方法建立了能源效率评价模型，对中国30个行政区域进行了实证研究;文献［6］提出基于非意愿变量Ruggiero三阶段模型对1998～2008年我国29个省级地区进行评价，旨在求解生产过程中给定各种投入要素和产出水平下实现碳排放污染最小化的效率指标;文献［7］运用DEA方法构建能源效率评价模型，对2008年中国30个省级行政区域的能源效率状况进行实证研究和评述;文献［8］利用BCCDEA模型和Malmquist指数法，分别从静态和动态角度计算了中国29个省份1995～2009年的全要素碳排放绩效，并分析了其影响因素.

对于DEA方法在物流业的应用，文献［9］运用数据包络分析对2006～2008年各省市物流业的资源利用效率进行了分析;文献［10］提出了一种基于PCADEA模型的物流园区绩效评价模型，对物流园区的运营绩效进行评价研究;文献［11］运用DEA的CCR模型和“超效率”(SuperEfficiency)模型，对我国31个省、市、自治区2008年物流产业的投入产出效率进行实证研究;文献［12］利用DEA方法对江苏省物流产业效率及其整体有效性、技术有效性和规模有效性进行了分析;文献［13］构造了一种区域物流效率评价模型，利用DEA模型对湖南省的区域物流效率进行了评价.

可以发现，已有文献针对区域碳排放评价的研究较少，且对于DEA方法在物流业的应用，国内已有研究大多集中于针对整个物流行业的效率评价，而很少对物流行业的碳排放效率单独评价.虽然DEA方法本身可以选取多个指标，即可以建立多输入多输出的评价指标体系，但是选取指标时，由于受到计算结果精确性和计算方法的限制，指标的个数上还是会有所限制.对于运用DEA方法来说，决策单元数n与输入输出指标之和(m+s)最好满足2(m+s)≤n≤3(m+s)这种关系，且指标之间不能存在较强的相关性，因此，为了让输入输出指标和决策单元数满足上述关系，削弱各个指标间的相关性，增强DEA方法评价的准确度，文中先用主成分分析的方法对其进行处理，再运用DEA方法进行评价分析.

1 研究方法

主成分分析法(principal components analysis，PCA)以降维为主要思想，可以实现将多个变量转化为几个综合变量，即主成分，各主成分之间既互不相关，又能够反映原始变量的绝大部分的信息.以主成分来综合代表多个变量，简化了问题的处理.在实际问题中，大多有众多的影响因素，一般称这些影响因素为指标或者变量，这些指标都在不同程度上反映了所研究问题的某些信息，并且彼此之间有一定的相关性，因此导致所得信息有所重叠.主成分分析法能够利用降维的思想使得变量减少，且得到的信息量较多，更有效地解决问题.

数据包络分析可以用来评价部门间的相对有效性.该方法在确定一组输入输出评价指标的基础上，借助于数学规划将决策单元(DMU)投影到DEA的前沿面上，并通过比较决策单元偏离DEA前沿面的程度来评价它们的相对有效性［14］.DEA模型从形成开始，一直在被不断完善，期间经过了CCR模型、BCC模型、CCGSS模型、CCW模型及CCWH模型的发展.

利用常规DEA模型可以将非同质投入指标进行加总，并评价单元相对于生产前沿面上的技术效率，但其产出指标一般为价值指标等期望产出，对于污染物等非期望产出却不适用［5］.处理污染物DEA模型的已有方法主要包括污染物作投入处理法、曲线测度评价法、数据转换函数处理法及距离函数法，这4种方法各有利弊.其中污染物作投入处理法违背了实际的生产过程，曲线测度法求解方法比较复杂，距离函数法评价的效率值受主观因素的影响很大.数据转换函数处理法可以将越小越好的非期望产出转化为越大越好的期望产出，而且有效地保持了DEA模型的凸性和线性关系，是一种应用较为广泛地处理环境污染物的方法.文中采用数据转换函数法对产出指标中的非期望产出进行处理.为得出技术有效性和规模有效性，选取基于投入导向的BCC模型.BCC模型是建立在生产可能集T满足凸性、锥性、无效性和最小性的假设基础上的.当T的锥性条件不成立时，得到的就是BCC模型(Dε):

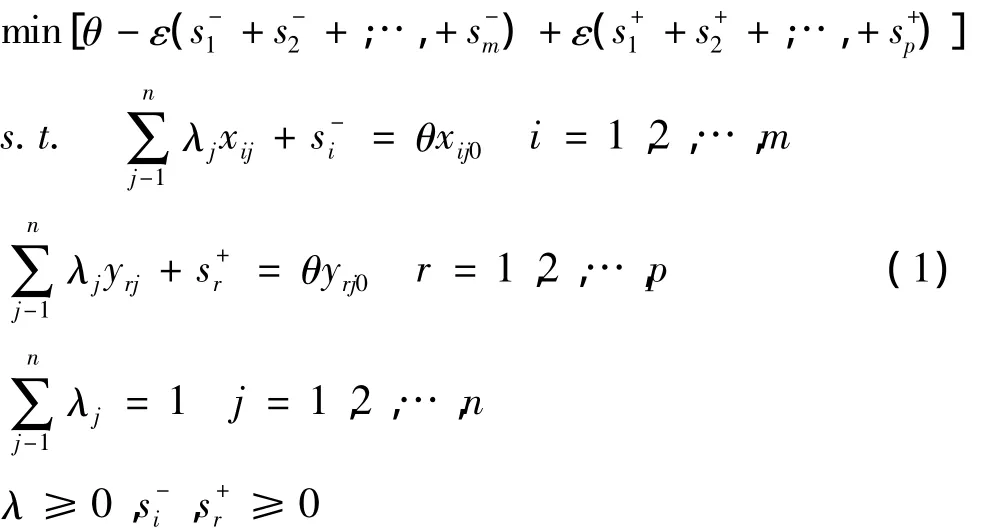
根据此模型求得的效率值为纯技术效率，同时还可以得到相应决策单元DMUj的规模效率(规模效率=技术效率C2R/纯技术效率B2C)，从而可将决策单元DMUj的效率值进行分解，进而分析无效决策单元低效率的原因.当计算出当θ*=1而且松弛变量s=0，=0时称决策单元DMUj为DMU有效，否则就称决策单元DMUj为DMU无效［15］.特别的，由C2R模型计算得到的是综合技术效率，B2C模型得到的是纯技术效率，又由规模效率=技术效率C2R/纯技术效率B2C，从而得到各个决策单元DMUj的规模效率及规模报酬.

2 实例研究

物流业的碳排放的来源主要由物流基础设施建设、社会物流运营、物流企业运营、物流平台与信息建设等几方面构成，文中对江苏省的13个城市的物流业碳排放效率进行评价，结合物流行业总体情况以及江苏省物流业发展的实际情况等，在此基础上构建了物流业碳排放效率的指标体系，以该指标体系为基础进行相关的计算与评价分析.选取了社会物流总额、物流业固定资产投资、货运周转量、载货汽车数量、境内公路里程、邮电业务收入、物流业从业人员、货运汽车能耗量这8个指标作为投入指标，将物流业增加值、货运汽车二氧化碳排放量两个指标作为产出变量.表1对具体指标体系与碳排放的关系及意义进行了简单的阐述.

表1 碳排放效率评价的指标体系Table1 Index system of evaluating carbon em issions efficiency

表2 各评价指标原始数据Table2 Raw data of each evaluation index

2.1 主成分分析

由于评价指标中投入指标较多，而且指标之间存在着一定的相关性，因而反映的信息在一定程度上会有所重叠，指标的相关性会影响DEA的分析结果.文中先利用主成分分析方法对8个投入指标进行降维处理，把原来较多的评价指标转化为较少的主成分指标，使指标之间互不相关.

利用SPSS18.0软件，将8个投入指标进行主成分分析处理，结果显示:Bartlett球体检验KMO值为0.540，显著性概率为0.000，故拒绝指标间不相关的原假设，适合做主成分分析.通过求初始公共因子特征值、方差贡献率及累计方差贡献率，按照特征根的大小从大到小依次排序.处理结果表明特征值大于1的主成分有3个，累计方差贡献率达到85.230%.所以提取出3个主成分比较合理.

通过因子得分系数矩阵可以得到所提取主成分的计算表达式:

其中:ZXi为各指标标准化后的数据，i=1，2，3，4， 5，6，7，8.

2.2 数据处理

因为二氧化碳排放量是非期望产出，首先通过线性数据转换函数法将各市的二氧化碳排放量进行转化，由负向效应转化为正向效应，由非期望产出转化为期望产出.

由于本例中的投入变量将由I1，I2，I33个新变量来代替，这3个变量均为13维列向量，由于这些数据中有些值为负数，不满足DEA运算的条件，所以，对新产生的这3个列向量进行处理，使它们均大于零.同时，由于投入、产出数据数量级差别比较大，而且具有不同的量纲，因此可以通过对数据进行处理来消除数据量纲的影响，同时使投入、产出数据变换到一个正区间内.选取文献［17］的处理方法，采用公式:

其中:xij为用主成分分析法计算得到的输入新变量;yij为产出变量;x'ij为转换后新的输入变量;y'ij为转换后新的产出变量.

转换后，输入指标x'ij∈［0.1，1］，输出指标y'ij∈［0.1，1］，得到新的输入变量和产出变量(见表3).

表3 处理后的输入变量和产出变量Table3 Input and output variables after processing

2.3 DEA评价与分析

将表3中新的输入变量和产出变量作为DEA模型的投入产出变量，运用DEAP 2.1软件对数据进行处理，得出江苏省各城市的碳排放效率(表4).

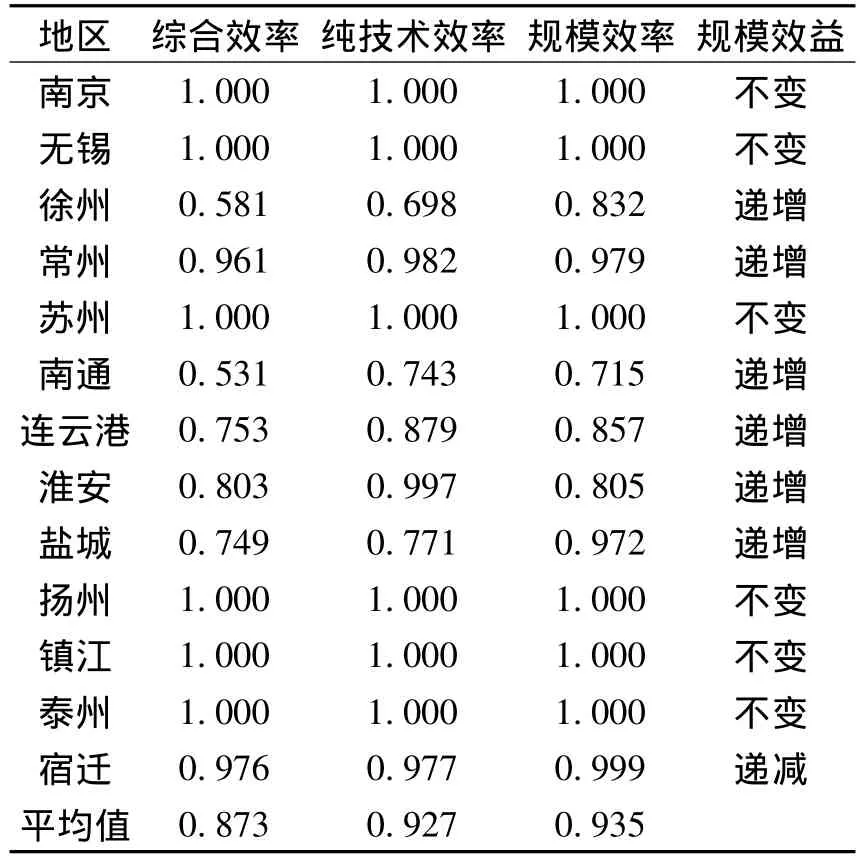
表4 DEA计算结果Table4 Results of DEA

从表4可以发现，在选取的13个城市中，南京、无锡、苏州、扬州、镇江、泰州这6个城市在综合效率、纯技术效率及规模效率上都达到了DEA有效，规模报酬不变，也就是说，这6个城市的碳排放效率是最好的.另外7个城市在综合效率、纯技术效率以及规模效率都没有达到DEA有效，即这些城市在投入上存在冗余或在产出上存在不足，保持现有的投入不变也仍有增加产出的空间，或即使减少投入也能够保持现有的产出水平.

其中徐州、常州、南通、连云港、淮安、盐城6个城市为规模报酬递增，也就是说这些区域如果将所有投入品的数量都以相同比例增加，将获得更大比例的回报;而宿迁市为规模报酬递减，则其在增加投入后，产出的增长比例会小于投入的增加比例，说明该城市物流产业发展规模的扩大没有得到有效地利用.以徐州为例，该城市物流业的碳排放综合效率值为0.581，属于DMU无效状态，其中，纯技术效率为0.698，规模效率为0.832，规模效益处于递增状态，说明该城市若想提高物流业的碳排放效率，需要调整产业结构，优化现有投入资源的配置，提高投入要素的生产效率，并适当提高物流业现有规模.

从表4可知，13个城市的物流业碳排放效率的规模效率的平均值为0.935，可以得出大部分城市在物流能耗效率上处于规模报酬递增状态，既想要等比例提高物流能耗效率时必须减少投入量，由此可见江苏省各城市的物流业碳排放效率大多处于集约型发展模式，比较符合现阶段国家倡导的低碳、绿色的发展理念.

通过对数据处理的结果，可以得出DEA无效城市的松弛变量分布(表5).

表5 DEA无效城市的松弛变量分布Table5 Distribution of slack variables in cities w ith invalid DEA

对于碳排放效率处于DEA无效的城市，可以根据它们的松弛变量的分布和数值来进行调整和改进.表5中，s，代表产出指标的松弛变量，，s2，s3代表投入指标的松弛变量，有松弛变量分布的地方就是可以进行投入和产出改进的地方，松弛变量数值的大小则是进行调整的大小.

从表5中可以看出，除南京、无锡、苏州、扬州、镇江及泰州这6个DEA有效的城市以外，常州、南通、连云港、淮安、盐城以及宿迁这几个城市在投入上存在冗余，可减少相应投入指标的投入量;徐州、常州、南通、连云港以及淮安这几个城市则在碳排放的正产出上没有达到最优，也就是碳排放仍有一定的减排空间.

以南通为例，结合表4来看，该城市物流业碳排放综合效率为0.531，总体效率较低，规模效益为递增，从表5可以看出，南通在第二个投入指标的松弛变量为0.416，相对来讲冗余较大，对应主成分分析结果，第二个主成分正影响最大的为境内公路里程和货运汽车能耗量.一方面说明南通市的道路没有得到有效的利用，另一方面说明南通市的货运汽车能耗浪费较严重，有可能存在空载及空返等问题，物流资源没有得到合理配置.该城市的碳排放输出指标松弛变量为0.281，也就是说，该城市可以通过改进技术、优化资源配置以及提高资源利用效率等方法，减少碳排放量，从而优化碳排放效率，促进物流业的可持续发展.

3 结论

文中以江苏省的物流业碳排放效率为对象，通过构建指标体系，采用主成分分析方法和DEA评价方法分析了江苏省13个城市物流业碳排放效率的DEA有效性、技术效率以及规模效益等情况，同时结合各DEA无效城市的松弛变量分布，对各城市的投入冗余和产出不足进行了一系列分析，提出了改善建议.

1 )以低碳物流为理念，江苏省的实际数据为背景，将主成分分析和DEA结合的方法应用到了物流业碳排放效率的评价中来，对江苏省乃至全国的物流业发展都有重要的意义.

2 )采用数据转化法巧妙地对碳排放这一非期望指标进行了处理.

3 )采用消除量纲法对数据进行了处理，使其满足DEA评价的要求.

通过对江苏省物流业碳排放效率进行DEA评价，发现大部分城市在物流能耗效率上处于规模报酬递增状态，由此可见江苏省各城市的物流业碳排放效率大多处于集约型发展模式，比较符合现阶段国家倡导的低碳、绿色的发展理念;通过对DEA无效城市的松弛变量分布进行分析，发现其DEA无效的主要原因在于投入上存在冗余，可减少相应指标的投入量，有针对性地从诸如提高道路有效利用率、合理配置物流资源、提高资源利用效率等方面做出努力.

References)

［1］ IEA.CO2emissions from fuel combustion 2008 edition［R］.［S.l.］:International Energy Agency(IEA)，Head of Communication and Information Office，2009.

［2］ Mielnik O，Goldemberg J.The evolution of the“Carbonization Index”in developing countries［J］.Energy Policy，1999，27(5):307308.

［3］ Ang BW.Is the energy intensity a less useful indicator than the carbon factor in the study of climate change［J］.Energy Policy，1999，27(5):943946.

［4］ Sun JW.The decrease of CO2emission intensity is decarbonization at national and global levels［J］.Energy Policy，2005，33(8):975978.

［5］ 吴琦，武春友.基于DEA的能源效率评价模型研究［J］.管理科学，2009，22(1):103112.

［6］ 李涛，傅强.中国省际碳排放效率研究［J］.统计研究，2011，28(7):6271.

Li Tao，Fu Qiang.Study on China's carbon dioxide emissions efficiency［J］.Statistical Research，2011，28 (7):6271.(in Chinese)

［7］ 刘炜晶，赵艳轲.基于DEA和因子分析的省际能源效率比较研究［J］.研究与探索，2011(7):107109.

［8］ 仲云云，仲伟周.中国区域全要素碳排放绩效及影响因素研究［J］.商业经济与管理，2012(243):8596.

Zhong Yunyun，Zhong Weizhou.China's regional total factors carbon emission performances and influencings factors anaysis［J］.Journal of Business Economics，2012(243):8596.(in Chinese)

［9］ 王舒鸿，汝慧萍，宋马林.基于DEA的物流行业能源效率评价:以2006年2008年各省市物流数据为例［J］.物流技术，2010(224):6668.

Wang Shuhong，Ru Huiping，Song Malin.Energy efficiency evalution of logistics industry based on DEA，illustrated with privincial logistics data from 2006 to 2008［J］.Logistics Technology，2010(224):6668.(in Chinese)

［11］ 雷勋平，Robin Qiu，刘思峰.基于DEA的物流产业效率测度实证研究:基于我国31个省、市、自治区2008年投入产出数据［J］.华东经济管理，2012，26 (7):6266.

Lei Xunping，Robin Qiu，Liu Sifeng.Empirical research on the efficiency measurement of logistics industry based on DEA model:based on inputoutput data in 2008 from 31 provinces，cities and autonomous regions of China［J］.East China Economic Management，2012，26(7):6266.(in Chinese)

［12］ 曾佑新，杜立奎.基于DEA的江苏省物流产业效率研究［J］.中国市场，2012，704(41):57.

［13］ 张媛，张革伕，解淑青.一种基于DEA的区域物流效率评价模型及其实证研究:以湖南省14个地市州为例［J］.物流工程与管理，2013，35(1):7679.

Zhang Yuan，Zhang Gefu，Xie Shuqing.Area logistics efficiency analysis based on DEA model:take the 14 cities in Hunan province for empirical analysis［J］.Logistics Engineering and Management，2013，35(1):7679.(in Chinese)

［14］ 魏权龄.数据包络分析［M］.北京:科学出版社，2004:2021.

［16］ 顾毓芳.2011年江苏省物流指数研究报告［M］.1版.北京:中国财富出版社，2012:3555.

［17］ 陈军飞，许长新，严以新.用数据包络分析法对港口水运上市公司经营效率的评价［J］.上海海运学院学报，2004，25(1):5155.

Chen Junfei，Xu Changxin，Yan Yixin.Research on the management efficiency of port and water-transportation corporations in the stock market based on the DEA method［J］.Journal of Shanghai Maritime University，2004，25(1):5155.(in Chinese)