风荷载效应作用下大矢跨比钢箱拱肋吊装过程稳定性分析

刘德鹏，王 林，彭 鑫

(江苏科技大学土木工程与建筑学院，江苏镇江212003)

传统钢筋混凝土拱桥由于自重大、施工架设困难等自身缺陷，跨越能力受到极大的限制.自上世纪50年代开始，钢箱拱肋拱桥由于其具有自重小、跨度大、材料单一、施工便捷等优点，因而钢箱拱肋拱桥逐渐成为当代大跨度拱桥建设的首选桥型.随着钢箱拱桥矢跨比的增大、结构的纤细，拱的稳定成为了一个制约拱桥跨径进一步增大和拱桥美观的最重要因素之一［1］.目前对于施工过程中静风荷载对大矢跨比钢箱拱肋整体稳定性的影响研究较少.风的静力作用除引起结构变位外，严重时会导致整个结构失稳，因此对于大跨径钢拱肋拱桥的静风稳定性问题应引起足够的重视，在这方面进行研究有很重要的实践意义［2］.

1 工程概况

伊克昭大桥位于康巴什新区东南部，是新区主干道伊克昭大街跨吉劳庆川的重要景观大桥.该桥为中承式钢箱拱肋系杆拱桥，主桥共设置三孔拱肋，三孔拱肋拱轴线在拱肋斜平面内均为二次抛物线.单孔两片拱肋间设置异形风撑，截面形式为矩形钢箱截面，中间孔拱为单箱双室断面，拱肋为全钢全焊结构，材质为Q345qE.拱轴线最高点距拱脚混凝土顶面的高度为67m(斜平面矢高)，计算跨径为130m，矢跨比为1.940，拱肋在横断面上的斜置倾角为12.8°;拱肋钢箱高度为3.5m，宽为3.8 m，壁厚为20mm;单片拱肋自重为425.6 t.

2 有限元模型

图1 1/2拱肋模型Fig.1 Half rib model

该桥施工采用整体提升吊装法.根据施工方提供的施工技术方案，其主要施工过程为:①场地硬化、胎架搭设，各拱肋在胎架上节段卧拼成1/4拱并进行焊接;②组装提升塔架，翻转拱肋，并调整好偏转角度;③缓慢提升拱肋吊点高度直至拱肋对接合拢，并完成拱肋、横撑合拢部位焊接.

文中主要研究1/2拱肋提升至设计高度时不同吊点位置对拱肋相对位移及内力的影响，为施工选取合理的吊点位置;同时，分析1/2拱肋采用单吊点起吊方案吊至设计高度时，不同风荷载工况下拱肋的失稳破坏机理.基于以上目的采用桥梁设计软件Midas/civil建立1/2拱肋模型(图1，2)，模型采用的单元类型为梁单元.Midas/civil中的梁单元被理想化为线单元，由2个节点构成，每个节点具有6个自由度(3个线自由度:Dx，Dy，Dz;3个转动自由度:Rx，Rx，Ry).梁单元以铁摩辛柯的梁理论(垂直于中和轴的截面，在变形后保持平面形状，但不一定要继续垂直于中和轴)为基础，分析时考虑剪切变形［3］.

图2 拱肋标准断面Fig.2 Standard rib section

3 吊点位置的选取

1 /2钢箱拱肋拱顶自地面位置起吊至设计高度过程中采用单吊点起吊，吊点位置是否合理直接关系到拱肋的整体稳定性，此外，拱肋在起吊过程中同时受到风荷载作用，分析可知，当拱顶起吊至设计高度，且风荷载与拱肋呈0°攻角时(即风力垂直作用于拱肋侧面)，拱肋变形处于最不利控制状态，且此时拱肋稳定性较差.因此取拱肋顶端起吊至设计高度时的状态进行分析(为便于研究，先不计风荷载效应影响)，应用有限元结构分析程序进行计算，求解出不同吊点位置下的拱肋相对位移、应力及支座反力(表1).

综合考虑起吊设备、施工情况、吊装安全系数等因素，分析表1知，选取55m作为吊点位置较为合适，此时拱端位移Δx，Δz适中，最大索力T= 2151.04 kN，考虑起吊动力系数取为1.3，求得吊索安全系数K=4.35，吊索安全［45］，图3为1/2拱肋起吊至设计高度时的吊点位置示意图.计入风荷载效应影响(设计风速v=40.24m·s1)，拱顶自地面位置起吊至设计高度过程中，拱肋整体稳定安全系数K见表2.由表2可知K＞5，符合规范要求(根据《公路桥涵设计通用规范》(JTG D602004)，对于拱肋宽跨比小于1/20的拱桥，必须进行成拱阶段拱的面内、面外稳定承载力验算，对于大跨度拱桥和无支架施工的拱桥，规定拱肋稳定系数K＞5).

表1 恒载作用下吊点位置与拱肋相对位移、应力及支反力关系Table1 Hanging point under dead load position and the relative rib displacements，stresses，and reaction forces relational tables

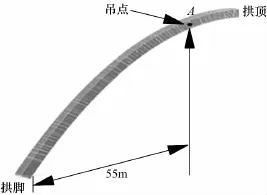
图3 拱肋吊点位置示意Fig.3 Schematic diagram of arch rib hoisting position

表2 拱肋稳定安全系数KTable2 Rib stability safety factor K

4 风荷载作用下拱肋吊装过程有限元分析

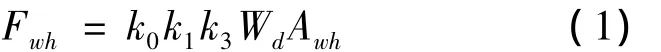
式中:Wd=，W0=，γ=0.012017e－0.0001z， Vd=k2k5V10.Fwh，W0，Wd，Awh，k0，k1，k2，k3，k5，γ等各参数的物理意义及取值均可由规范查得.

由公式计算可得，将风力简化为作用在拱肋上按梯形分布的荷载时，拱脚处的荷载集度为4.948 kN/m，拱顶处的荷载集度为7.851 kN/m.

文中采用3种不同的加载工况对风荷载效应影响进行对比分析［5］:工况1，横向水平风荷载作用(0°初始攻角);工况2，斜桥向水平风荷载作用(45°初始攻角);工况3，纵向水平风荷载作用(90°初始攻角).

通过有限元程序计算得到3种工况下1/2拱肋相对线位移Δxyz，max、扭转角位移Rxyz，max、以及拱肋最大正应力σxyz，max随风速的变化关系(图4，5，6).

图4为工况1拱肋相对线位移、相对扭转角位移以及拱肋最大正应力的有限元程序计算结果.图中曲线均具有非线性的增长规律.随着风速的增加，当风速 v小于 60 m·s1时，相对线位移Δxyz，max、扭转角位移 Rxyz，max、以及拱肋最大正应力σxyz，max均呈线性变化，非线性特征较弱(1/2拱肋实际为带悬臂端的简支梁，由于此简支梁跨度较小且悬臂端较短，拱肋整体刚度较大);当风速v大于60m·s1，小于210m·s1时拱肋相对线位移Δxyz，max非线性特征明显，增长速度加快，而拱肋扭转角位移Rxyz，max呈直线递增趋势，非线性效应不明显;当风速v增加至210m·s1时，风速稍有增加，便能引起拱肋相对线位移Δxyz，max产生较大幅度的增长，此时，结构已开始出现了拱肋静力失稳，对比图4a)，b)，c)知，失稳时结构拱肋截面相对线位移Δxyz，max的非线性效应较拱肋扭转角位移 Rxyz，max的更加明显，且拱肋最大应力σxyz，max变化趋势与相对线位移Δxyz，max基本一致，说明该钢管混凝土拱桥的拱肋失稳形式为以横向线位移为主的空间弯剪耦合失稳［6］.

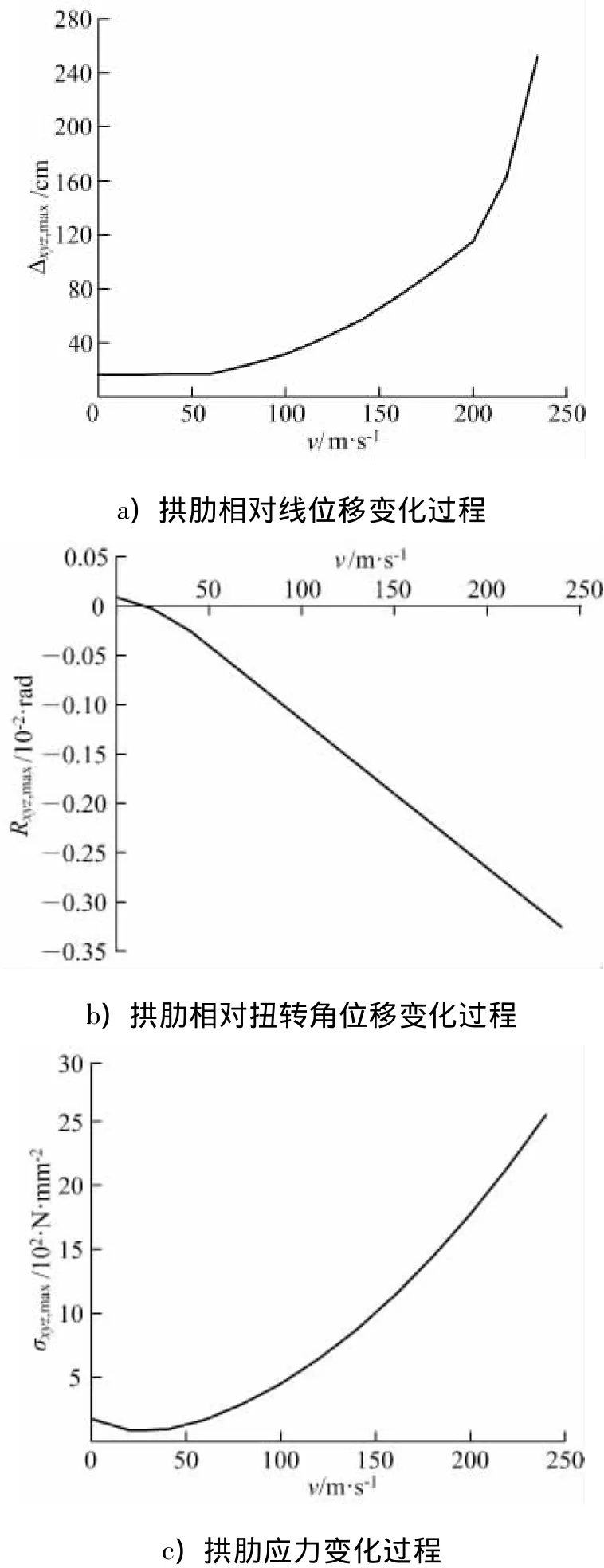
图4 工况1拱肋空间相对位移及应力与横向风速变化关系Fig.4 Rib space relative lateral displacement and stress and variation of w ind speed

图5为工况2拱肋相对线位移、相对扭转角位移以及拱肋最大正应力的有限元程序计算结果.对比图4a)，图6a)，不难看出拱肋相对线位移自0m·s1起即呈非线性增长，随着风速v的增加非线性特征逐渐明显，且数值相对工况1、工况3均较大(风力以45°攻角作用于拱肋时，有效风荷载作用面积最大，拱肋所受风荷载最大).分析图5b)，c)可知，相对扭转角位移Rxyz，max、拱肋应力σxyz，max变化趋势分别与图4b)，c)相似，相对数值大小介于工况1和工况3之间，这一点与上述相对线位移结果不同.对比图4b)可知，风力攻角θ=45°时，随着风速v增加，扭转角位移Rxyz，max线形变化并不明显，改变量均小于0.0005 rad.可见，此时1/2钢箱拱肋失稳形式为以横向线性变形为主的空间弯剪耦合失稳，由风荷载效应引起的扭转变形对拱肋失稳产生的不利影响仍较弱［7］.

图5 工况2拱肋空间相对位移及应力与斜桥向风速变化关系Fig.5 Rib space relative obliquel displacement and stress and variation of w ind speed

图6为工况3拱肋相对线位移、相对扭转角位移以及拱肋最大正应力的有限元程序计算结果，分析图6a)知，当v小于200m·s1时，最大相对线位移Δxyz，max基本呈线性变化，非线性特征不明显(悬臂端有效风荷载作用面积较小，最大相对线位移Δxyz，max发生在简支梁部分，但由于此简支梁实际为两端简支的拱，对作用其顶部的风荷载有足够的抵抗刚度整体，故随着风速的增加，结构位移很不明显).分析图6b)知，当v小于160m·s1，扭转角位移Rxyz，max接近直线增长，非线性特征并不明显，(相对扭转角位移Rxyz，max发生在悬臂端，虽然有效风荷载作用面积较小，但由于悬臂端的自重作用，风荷载效应与自重作用两者耦合使得扭转角位移Rxyz，max增长幅度较大)，此时拱肋仍处于弹性阶段.当v处于160～200m·s1范围内时，随着风速增加，Rxyz，max开始表现出明显的非线性特征;当v超过200m·s1，即使风速不再增加，扭转相对角位移Rxyz，max仍不断增长，此时，结构已开始出现了屈曲失稳现象，对比图6a)，b)，c)知，失稳时结构拱肋截面相对扭转角位移Rxyz，max的非线性效应较拱肋相对线位移Δxyz，max的更加明显，且拱肋最大应力σxyz，max变化趋势与相对线位移Rxyz，max基本一致，说明该1/2钢箱拱肋失稳形式为以扭转角位移为主的空间弯扭耦合失稳.

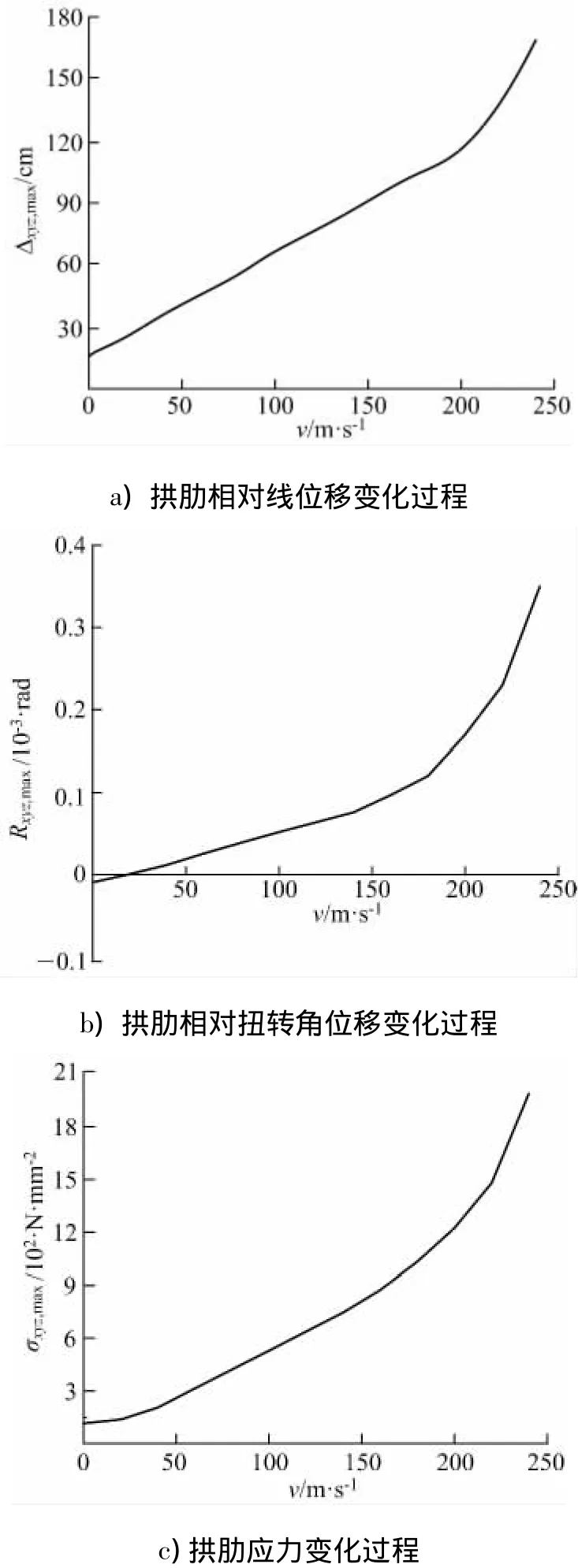
图6 工况3拱肋空间相对位移及应力与纵向风速变化关系Fig.6 Rib space relative longitudinal displacement and stress and variation of wind speed

同时，通过有限元程序计算得3种不同工况下拱肋稳定安全系数(表3).分析表3得:工况1风荷载作用下，随着风速的逐渐增加，1/2拱肋的整体稳定性明显减弱，K值变化较大，当风速v≤210m·s1时，K＞5，符合规范要求;v≥220m·s1时，K＜4，通过程序计算结果知极限风速v=218m·s1，v＞218m·s1时，结构失稳.工况3风荷载作用下，随着风速的增加，当v≤195m·s1时，K＞5，结构稳定，由程序计算得极限风速v=198m·s1，v＞198m·s1时，结构失稳.对比工况1和工况3可知，工况2相应风速下K值基本取上述两工况下对应K值的中间值，当v≤200m·s1时，K＞5，结构稳定，由程序计算得极限风速v=207m ·s1，v＞207m·s1时，结构失稳.以上分析所得结论与图4，5，6分析结果基本一致.

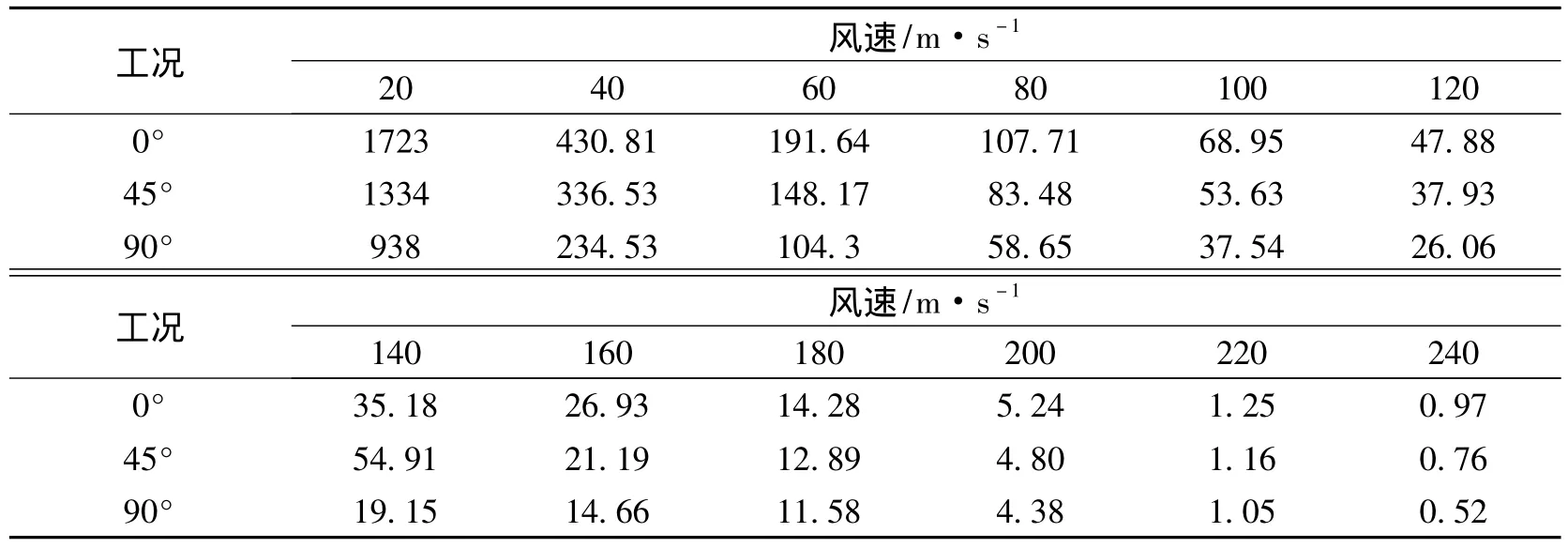
表3 拱肋屈曲稳定系数KTable3 Rib buckling stability factor K

5 结论

文中通过对1/2拱肋采用单吊起吊时不同吊点位置拱肋相变形、应力、吊索索力以及支反力的对比分析，得出合理的单吊点起吊方案，希望能为同类桥型的设计与施工提供借鉴和参考.同时得出以下结论:

1 )1/2拱肋单吊点起吊过程中，设计风速对拱肋整体稳定性影响较小(稳定安全系数K远大于5)，一般可忽略不计;

2 )当1/2拱肋采用单吊点起吊，拱肋顶端吊至设计高度时，拱肋整体稳定性受风荷载效应影响明显，当风速达到一定数值时，拱肋将发生不同形式的失稳破坏;

3 )当以横向风荷载作用为主时，随着风速的增加，拱肋失稳形式为以横向位移为主的空间弯剪耦合失稳;

4 )当以纵向风荷载作用为主时，随着风速的增加，拱肋失稳形式为以扭转角位移为主的空间弯扭耦合失稳;

5 )当风荷载沿斜桥向(θ=45°作用于拱肋侧面时，1/2钢箱拱肋失稳形式为以横向线性变形为主的空间弯剪耦合失稳，由风荷载效应引起的扭转变形对拱肋失稳产生的不利影响仍较弱，可忽略不计.

通过上述分析结果可知，风荷载效应对大矢跨比钢箱拱桥拱肋吊装过程中稳定性的影响不容忽视，风速越大，影响越明显，且随着风荷载作用方向的变化，结构失稳机理差异很大.因此，当拱肋采用单吊点起吊方案进行起吊时，应根据外界不同风荷载作用采取必要的保护措施，以期减小风荷载效应对吊装过程中拱肋的不利影响.

References)

［1］ 颜全胜，李立军.大跨度钢管混凝土拱桥的非线性空气静力稳定性［J］.华南理工大学学报:自然科学版，2005，33(12):8791.

Yan Quansheng，Li Lijun.Nonlinear aerostatic stability of long-span concrete-filled steel-tube arch bridge［J］.Journal of South China University of Technology:Natural Science Edition，2005，33(12):8791.(in Chinese)

［2］ 陈峰，胡大琳.大跨径钢管混凝土拱桥非线性静风稳定性［J］.长安大学学报:自然科学版，2006，26(2):4246.

Chen Feng，Hu Dalin.Aerostatics stability of longspan concrete-filled steel tube arch bridge［J］.Journal of Chang'an University:Natural Science Edition，2006，26 (2):4246.(in Chinese)

［3］ 王元清，姜波，张勇，等.静风荷载对大跨度钢管砼拱桥施工稳定性的影响［J］.重庆交通大学学报:自然科版，2007，26(4):4650.

Wang Yuanqing，Jiang Bo，Zhang Yong，et al.Influences ofwind load on the stability of concrete filled steel tube arch bridge in construction［J］.Journal of Chong Qing Jiaotong University:Natural Science Edition，2007，26 (4):4650.(in Chinese)

［4］ 张建民，寇素霞.风荷载作用下钢管混凝土拱桥反应几何非线性有限元分析［J］.东北林业大学学报，2005，33(5):120122.

Zhang Jianmin，Kou Suxia.Analysis of concrete-filled steel-tube arch bridge forced by the wind load with nonliner finite element method［J］.Journal of Northeast Forestry University，2005，33(5):120122.(in Chinese)

［5］ 李东兴，陈学军，徐亚婷，等.复杂条件下钢拱桥整体吊装技术［J］.施工技术，2010，39(11):9698.

Li Dongxing，Chen Xuejun，Xu Yating，et al.Integral hoisting technology of steel arch bridge with rope under complicated conditions［J］.Construction Technology，2010，39(11):9698.(in Chinese)

［6］ 李世清，黄传胜，徐剑中，等.钢管混凝土拱桥整体吊装法施工的静力分析及稳定性研究［J］.世界桥梁，2005(3):5660.

Li Shiqing，Huang Chuansheng，Xu Jianzhong，etal.Static analysis and stability study of concrete-filled steel tube arch bridge being erected by integral liftingmethod［J］.World Bridges，2005(3):5660.(in Chinese)

［7］ 张益多，鲍丽丽，李年维，等.京沪高铁96m系杆拱桥施工过程有限元分析［J］.江苏科技大学学报:自然科学版，2012，26(1):1822.

Zhang Yiduo，Bao Lili，Li Nianwei，et al.The finite element analysis on construction process of the 96 m span tied-arch bridge in Beijing-Shanghai express railway［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2012，26(1):1822.(in Chinese)