风浪流成长全过程单点系泊FPSO运动低频响应极值研究

窦培林，朱 建，陈 刚，施兴华，袁洪涛

(1.江苏科技大学船舶与海洋工程学院，江苏镇江212003)

(2.广州船舶及海洋工程设计研究院，广东广州510250)

(3.上海外高桥造船有限公司，上海200137)

在海洋中生产运营的FPSO，时刻受到不断变化的风浪流等环境载荷的影响，且最危险环境条件与风浪流等变量之间的关系密切相关［12］.为了使其能安全的生产作业，避免海损事故的发生，正确评估不同风浪流载荷作用下FPSO的运动响应显得尤为重要.

单点系泊FPSO的一个重要特点是具有风标效应(weather vane)，风标效应对FPSO最直接的作用就在于对船体首摇角的控制，使得FPSO船艏能够尽量稳定地保持最有利方向，始终处于最小受力状态［3］.文献［4］中研究表明浪的发展可以分为发展、顶峰、衰亡3个阶段，其中发展和衰亡阶段的定义以顶峰阶段最大有义波高的33%为界.且根据实际海域监测发现在发展、衰亡阶段，风与浪入射角度呈强烈非线性，最大交角达149°;在顶峰阶段，风与浪入射角度共线性明显，夹角在0°～30°范围.文献［2］中研究发现FPSO在与穿梭油轮外输作业时，当风与浪入射夹角为60°～90°的情况时，连接缆张力达到最大值.文献［5］中认为风浪流入射夹角都为30°时为百年一遇最恶劣海况，并进行了FPSO与系泊系统、立管时域耦合分析计算出各系缆的张力值.但关于风浪流之间的入射夹角对FPSO低频运动响应的影响，特别是针对风浪流发展的各个阶段对应的FPSO低频运动响应的研究甚少，未见报道.

文中运用优化计算的方法，在合理的风浪流入射夹角范围之内，研究了纵荡、横荡、首摇运动响应对应的最危险的风浪流入射角度，分析了在风浪流载荷为发展、顶峰、消亡各不同阶段对应的船体低频运动响应，进一步认识了单点系泊FPSO低频响应与风浪流入射角度之间的关系，以及在风浪流发展各个阶段的低频响应特性，为系泊系统的设计及船体极限强度等的研究提供有益参考.

1 理论基础

1.1 时域运动方程

根据三维势流理论［6］计算频域下的波浪力传递函数、附加质量、附加阻尼、幅值响应算子等水动力参数，通过傅里叶变换及Cummins脉冲理论进行时域分析，其波频运动方程为:

其低频运动方程［7］为:

式中:m为浮体质量;I为惯性矩;x(2)为低频运动; Bwdd为纵荡波浪慢漂阻尼系数;F为流引起的动载荷;F为风引起的动载荷;F为系泊力;F为二阶波浪漂移力;B11，B22，B66为阻尼系数.此外，文中系缆阻尼以拖拽力系数来模拟.

1.2 环境载荷计算

1.2.1 风载荷计算

在海洋结构物的风载荷计算中将风作为均匀风来处理，不同入射角度的风对应不同的风系数，其风载荷计算公式为:

式中:第1项为力，第2项为力矩，V为风相对于浮体运动的相对风速;ρa为空气密度;Aa为浮体在风速方向上的投影面积;L为力作用点到平台重心的距离; Cdw为风阻力系数，文中的风阻力系数根据CCS颁布的“海上单点系泊装置入级与建造规范”确定.

1.2.2 流载荷计算

在海洋结构物流载荷的计算中，通常将其视为定常力，不同流的入射方向对应不同的流系数，其流载荷的计算公式为:

1.2.3 波浪载荷计算

波浪与浮体的相互作用表现为3种力作用在系泊浮体上:①以波浪频率振荡的一阶力;②以低于波频振荡的二阶力(缓变漂移力);③二阶力中的定常部分.文中采用Newman［89］近似的方法利用二阶定常力估计缓变漂移力，其中定常力部分计算公式为:式中:i取1，2和6分别表示纵向漂移力、横向漂移力和首摇漂移力矩;C(w，a)为波浪相对于浮体呈a角时的波浪漂移系数;S(w)为海浪谱;在波浪入射方向确定后，根据上式计算不同频率的波浪漂移力累计求平均值，即得二阶定常力.

2 单点系泊FPSO

文中对一艘20万吨级单点系泊FPSO在作业水深为1500m海域下进行低频运动响应数值分析.首先在SESAM/GeniE中建立水动力面元模型，如图1所示;然后在SESAM/Hydrod中应用势流理论进行规则波频域分析，将水动力参数数据库保存为G文件，导入DeepC进行全时域耦合分析，采用JONSWAP谱模拟波浪载荷，NPD谱模拟风载荷.系泊系统由4组各4根总共16根组成，同一组系缆间夹角为5°，系泊缆参数如表1所示;采用内转塔式系泊，内转塔位置距艏柱距离为船体垂线间长的7.3%，如图2所示.表2为FPSO主要参数.

图1 FPSO水动力面元模型Fig.1 Hydrodynam ic panelmodel of FPSO

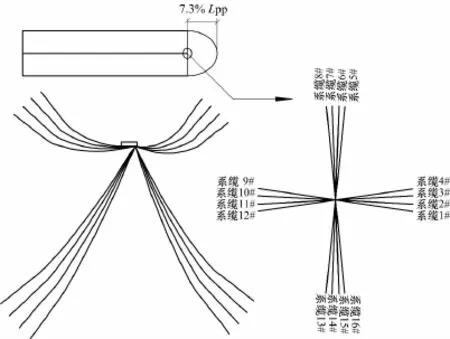
图2 FPSO系泊系统布置Fig.2 Arrangement ofmooring system

表1 悬链式系泊缆主要参数Table1 Parameters of catenary line

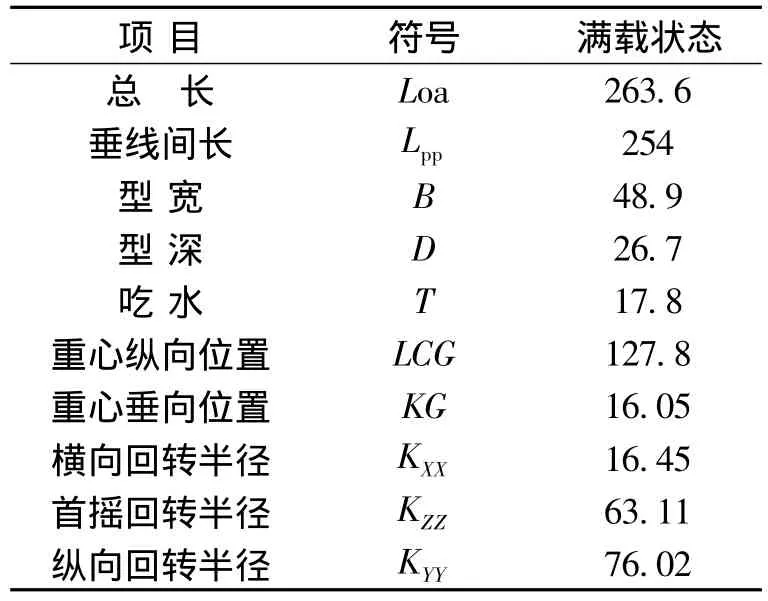
表2 FPSO主要参数Table2 Main particulars of FPSO m

3 计算结果及分析

在FPSO运动响应分析中，低频运动响应即纵荡、横荡、首摇相对于垂荡、横摇、纵摇响应更大，对于系泊系统张力和船体结构动力响应产生更大的影响，所以本文将详细分析不同风浪流的入射角度以及风浪流发展的不同阶段对低频运动响应的影响.

3.1 单点系泊FPSO低频运动响应风浪流最危险入射角度研究

对于纵荡运动响应，先考虑风与浪两种因素，固定浪入射角度，风的角度在某一范围内自动搜索，如图3a)所示wind1～wind2，且与浪入射方向夹角最大不超过60°［10］，找到最大响应值即停止搜索，固定此时风与浪的入射角度;接着加进流的因素，在180°范围内自动搜索［11］，如图3b)中current1～current2，找到最大响应对应流的入射角度，固定风与流的入射角度不变，然后搜索浪的角度，如图3c)中wave1～wave2;以此类推，不断循环(图3)，当每一个环境因素前后两次搜索响应差值都在5%之内即停止搜索，得到纵荡响应的最危险风浪流入射角度.同理，横荡与首摇运动响应也采用上述方法计算得到最危险的风浪流入射角度.在上述计算中，所用环境参数如表3所示.

图3 风浪流危险入射角计算方法Fig.3 M ethod of calculate w ind/wave/current incident angle

表3 环境参数Table3 Environment condition

在表4中，工况1即通常认为对于FPSO百年一遇海况对应的风浪流入射角度，工况2、工况3、工况4分别代表用上述方法计算得出的纵荡、横荡、首摇对应的风浪流最危险入射角度θ;图4～6给出了每一低频自由度常规响应与极限响应时间t，位移S的曲线对比，表5给出了低频运动响应对应的统计值.

表4 低频极限响应对应风浪流入射角度Table4 W ind/wave/current incident angle to low frequency extreme response

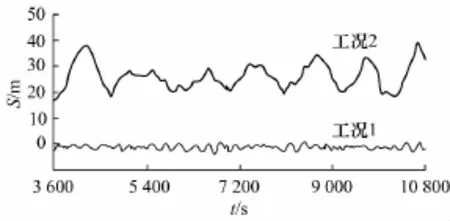
图4 常规工况与极限工况纵荡响应对比Fig.4 Comparison the time history of surge in common and extreme condition

图5 常规工况与极限工况横荡响应对比Fig.5 Comparison the time history of sway in common and extreme condition

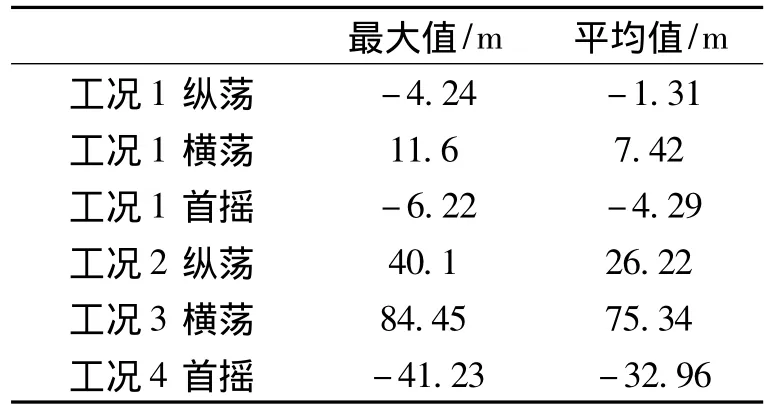
表5 低频运动响应统计值Table5 Statistics of low-frequency motion response

图4～6及表5表明，纵荡、横荡、首摇极限响应的最大值分别是常规计算情况的9.5，7.3，6.6倍.至于出现巨大差异的原因，以横荡为例进行说明.图7a)为横荡响应的最危险风浪流入射角度，即工况3作用下对应的静力平衡位置;图7b)为常规百年一遇工况，即工况1作用下对应的静力平衡位置;工况3作用下，船体首摇角在37°～24°之间变化(图7a))，且流入射角度为90°，相比于图7b)流入射角度，流系数增大1倍，再综合考虑流载荷作用面积等因素，横荡方向流载荷相比于常规百年一遇海况至少增大了2.5倍(Fcurrent=CdcρwAV2)以上，且常规百年一遇海况风浪流入射角度(图7b))还会出现风流载荷相抵消的情况，所以横荡方向流载荷的巨大差异将会导致横荡响应极值急剧增大情况的发生.因此对单点系泊FPSO进行低频运动响应分析的时候，除了风浪流绝对大小对响应有很大影响外，风浪流的入射角度同样至关重要.

图7 首摇响应示意Fig.7 Sway motion response in common and extreme condition

3.2 风浪流发展的各个阶段单点系泊FPSO低频运动性能

文中将风浪流的成长分为发展、顶峰、衰亡3个阶段，其中发展和衰亡期的定义以顶峰期最大有义波高、最大风速、最大表面流速的33%为界［4］(表6).顶峰阶段风浪流入射角共线性明显［4］，取常规的百年一遇海况定义的风浪流入射角度150°/180°/ 210°为极限海况;发展和衰亡阶段，风浪流入射角呈强非线性［4］，取上一节计算结果为极限海况，即对于纵荡、横荡、首摇风浪流入射角度分别为:120°/ 180°/90°，125°/170°/90°，120°/180°/100°，计算得纵荡、横荡、首摇三自由度在顶峰阶段和发展、衰亡阶段的运动响应时间历程曲线对比(图8～10)，表7给出了相应低频运动响应的统计值.

表6 风浪流发展的各个阶段的参数Table6 Environment condition in different stages

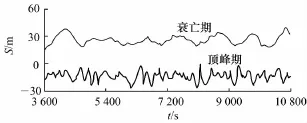
图8 发展或衰亡期与顶峰期纵荡响应对比Fig.8 Comparison the time history of surge in development/decay and peak stage

图10 发展或衰亡期与顶峰期首摇响应对比Fig.1 0 Comparison the time history of surge in development/decay and peak stage

图9 发展或衰亡期与顶峰期纵横响应对比Fig.9 Comparison the time history of sway in development/decay and peak stage

表7 低频运动响应统计值Table7 Statistics of low-frequency motion response

由图8～10及表7表明，纵荡、横荡、首摇在发展或衰亡阶段运动响应极值是通常计算的顶峰阶段响应最大值的1.4，5.7，3.3倍.由此表明，并不是风浪流成长到顶峰阶段时对应的单点系泊FPSO低频响应才是最大的，而有可能在风浪流绝对大小较小但入射角度呈强非线性的发展或衰亡阶段，当风浪流入射角度呈现某些组合时，会出现相比于顶峰阶段更大的运动响应，对FPSO及其系泊系统造成巨大损伤，这一点应引起足够的重视.特别需要指出的是，FPSO及其系泊系统有可能在顶峰阶段已经出现了某种程度上的损伤，此时再进入衰减阶段遇到更恶劣的环境条件导致更大的船体运动响应与系缆动力响应，有可能会造成整套系泊系统损毁，立管等输油管线断裂，FPSO在海上任意漂流的严重后果.

因此定义单点系泊FPSO极限海况时，有义波高、风速、流速的绝对大小并不是唯一指标，还要结合实际工作海域，与风浪流成长全过程中可能出现的风浪流入射角度综合考虑.

4 结论

1 )纵荡、横荡、首摇对应不同的风浪流危险入射角度，且这些入射角度并不是唯一确定的，它需要根据不同海况、不同船型计算确定;

2 )对于单点系泊FPSO，低频运动响应极值可能并不出现在有义波高、风速、流速最大的顶峰阶段，而是出现在有义波高、风速、流速较小，但入射角度呈强非线性的发展或衰减阶段.因此，在进行单点系泊FPSO低频运动响应分析时，必须考虑风浪流的发展或者衰亡阶段;

3 )对于单点系泊FPSO百年一遇极限海况，并不能简单地以有义波高、风速、流速的绝对大小来定义，应结合实际工作海域海况与风浪流成长全过程中可能出现的风浪流入射角度综合考虑.

References)

［1］ Yilmaz O，Incecik A.Dynamic response of compliant offshore platforms to non-collinear wave，wind and current loading［C］∥Proceedingsof the Sixth Conferenceof ICOSSAR'93 on Structural Safety and Reliability.Innsbruck，Austria:［s.n.］，1993:913.

［2］ Yilmaz O，Incecik A.Hydrodynamic design ofmoored floating platforms［J］.Marine Structures，1996(9):54575.

［3］ Liu F，Brown D T.Turret moored floating production system response with varying turret location and wind direction［C］∥Proceedings of the OMAE.Lisbon:［s.n.］，1998.

［4］ Bowers JA，Morton ID，Mould G I.Directional statistics ofwind and waves［J］.Applied ocean research，2000，22: 1330.

［5］ Kim M H，Koo B J，Mercier R M，et al.Vessel/mooring/ riser coupled dynamic analysis of a turret-moored FPSO compared with OTRC experiment［J］.Ocean Engineering，2005，32:17801802.

［6］ 戴遗山，段文洋.船舶在波浪中运动的势流理论［M］.北京:国防工业出版社，2008:6390.

［7］ 戴遗山.舰船在波浪中运动的频域与时域势流理论［M］.北京:国防工业出版社，1998.

［8］ Newman JN.Marine hydrodynamics［M］.Cambridge，Massachusetts，USA:The MIT Press，1977:102131.

［9］ Newman JN.Slowly-varying forces on vessels in irregular waves［C］∥International Symposium on the Dynamics of Marine Vehicles and Structures in Waves.London: University College，1974.

［10］ BV NR493.Classification ofmooring systems for permanent offshore units［R］.Burean Veritas，Paris，2012.

［11］ 李欣.软钢臂系泊FPSO水动力响应研究［D］.上海:上海交通大学，2005.