围岩破损区的时效模型探讨
程丽娟,李建华,彭薇薇
(中国水电顾问集团成都勘测设计研究院有限公司,四川 成都 610072)
0 引 言
开挖扰动形成的洞周围岩破损区根据扰动程度可以分为塑性区和开挖破裂区,如图1所示。与处于弹性区的岩体相比,破损区岩体是洞周变形的主要贡献者:塑性区岩体是洞室开挖应力调整后的主要承载圈,其短期力学性质尚未发生明显弱化,但由于其所处应力水平较高,岩体处于长期高水平的应力作用下容易发生不可忽视的时效变形,岩体的力学性质也会随着时效变形进一步弱化,使得破损区往深部扩展[1];破裂区岩体已经进入不连续状态,其力学性质已然弱化,长期强度显著降低,因此即便破裂区岩体处于部分应力已经释放的状态,依然容易出现时效变形现象,它是洞周岩体施工期稳定性和长期稳定性的潜在威胁。引起洞室围岩时效变形甚至失稳的主因是破损区岩体流变特性中的蠕变性质[2-3],对岩体流变特性进行研究是合理设计支护、保证地下洞室围岩长期稳定的前提。
针对岩体的流变特性,国内外学者先后进行过大量力学试验,分析并提出众多力学模型对其进行描述,其中工程应用最广的是元件流变模型[4-6]。元件模型理论将三种基本变形特征用相应的元件来描述:描述弹性变形的弹簧(Hooke体)、描述粘性变形的粘壶(Newton体)和描述理想塑性流动的摩阻片(St. Venant体)。并用这三种基本元件的各种组合来描述材料的各种复杂变形特征。但是,理想的塑性流动在岩土工程中并不多见,尤其对于处在单向甚至双向卸荷状态下的洞周岩体而言,随着塑性变形的积累岩体材料更容易出现应变强化和应变软化[7-8]。因此用传统的St. Venant体描述塑性变形已经不能满足岩土类材料的需求。此外,从三种基本元件的性质可以看出,元件模型无法模拟加速蠕变,也就是说传统的元件流变模型不能模拟蠕变破坏(即稳态蠕变往加速蠕变过渡),为此有学者采用非线性粘性元件代替Newton体来模拟加速蠕变,根据加速蠕变曲线的特点,一般假定应变与时间成幂律关系,通过调整指数来模拟加速蠕变出现的时间[9-12]。而实际上,在不同应力状态下应变与时间的关系不同,这一点在上述非线性粘性元件中未曾考虑。因此,蠕变破坏准则一直是元件流变模型未能较好解决的问题。

图1 地下洞室开挖扰动区分区示意
本文将塑性位势理论[13]引入元件流变模型,基于“不可逆变形难以区分出塑性部分和不可逆粘性部分”的认识,建立了一种适用于描述围岩破损区演化的时效本构模型,该模型统一了蠕变破坏与瞬时变形破坏的破坏准则,从破坏准则的角度找到了稳态蠕变向加速蠕变过渡的起始点,因此可以较好的描述从衰减蠕变、稳态蠕变到加速蠕变的全蠕变阶段,更真实的反映围岩破损区岩体的时效变形特点。
1 围岩破损区的时效模型推导
如上文所述,元件流变模型中,传统的St.Venant体描述塑性变形不能满足岩土工程需求,考虑到材料的粘塑性变形(或者称为不可逆变形)难以区分出塑性部分和不可逆粘性部分,二者也互相影响,可以将二者统一用粘塑性变形来表示,因此本文提出一种非定常St.Venant体(图2中圆圈中的元件),并与传统St.Venant体和Newton体组合成复合型粘塑性体(图2中虚线框中的组合元件),该模型中塑性变形由非定常St.Venant体的屈服条件控制,不可逆粘性变形则由传统St.Venant体的长期强度条件控制。此外,材料的瞬时弹性性质可以由Hooke体表征,粘弹性性质由Kelvin体(由Hooke体和Newton体并联而成)表征,因此一维剪应力条件下的流变模型如图2所示。

图2 剪应力作用下的一维模型
图2中描述弹性变形的Hooke体具有如下本构方程:
(1)
式中τ——为剪应力;
G1——为Hooke体的剪切模量;
γe——为弹性剪应变。
描述粘弹性变形为Kelvin体具有如下本构关系:
(2)
式中η2——为Kelvin体的粘滞系数;
G2——为Kelvin体的剪切模量;
γve——为粘弹性剪应变;

粘塑性变形也属于不可逆塑性变形范畴,假设粘塑性变形满足塑性位势理论定义的塑性流动方式,即:
(3)
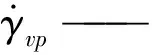
α——为粘塑性因子;
Q——为塑性势函数。
塑性变形与应力历史相关,不能显式定义全量型本构关系,那么粘塑性变形的增量型本构关系可以定义为:
(4)
式中 Δλ——为塑性因子增量;
η——为图2中粘塑性体的粘滞系数;
τs——为屈服强度;
τ1——为长期强度;
Δt——为时间增量。
〈*〉为开关函数:〈*〉=*/2+|*|/2。当〈τ-τs〉>0时,材料发生塑性屈服,有塑性变形产生;当〈τ-τ1〉>0时,材料的应力状态超过长期强度[1],发生不可逆粘性变形。屈服强度τs是塑性变形历史的函数,即
(5)
对于具有强化软化性质的材料来说,屈服强度随塑性变形的增加先增大再减小直到残余强度(如图3所示),因此从式(4)可以看出:若当前应力状态τ小于当前的屈服强度而大于长期强度,那么在随后一段时间里会出现等速粘塑性蠕变,蠕变速率大小为式(4)的右端第二部分,即粘塑性变形持续等速增长,屈服强度τs也随之先增大到峰值再减小(见图3),当τs减小到τ-τs>0时,由屈服引起的塑性变形再次出现,若应力状态始终保持τ不变,而持续增长的粘塑性变形会使得屈服强度τs持续下降,〈τ-τs〉逐渐增大,就相当于在粘塑性体内部对塑性元件持续加载,这个过程的粘塑性变形速率为式(4),描述加速粘塑性变形过程,即加速蠕变阶段,发生蠕变破坏。因此式(4)对粘塑性本构关系的定义符合人们对长期强度的认识。
在三维条件下,一点的应力状态是一个二阶对称张量,应力张量可以分解为球应力张量和偏应力张量,写成指标形式为:
σij=σmδij+sij
(6)
式中σij——为应力张量;
σm=σkk/3——为球应力;
δij——为Kronecker delta符号(i=j时,δij=1;i≠j时,δij=0);
sij——为偏应力张量。
相同,应变张量也可以分解为球应变(体积应变的1/3)张量与偏应变张量之和:
εij=eij+εvolδij/3
(7)
式中εij——为应变张量;
eij——为偏应变张量。
体积应变εvol=εkk。
考虑到塑性变形不能用显式的全量关系表示,将应变张量写成增量型式,根据图2所示的各元件之间的关系,总的球应变和偏应变张量分别由以下几部分组成:
(8)
式中 Δeij——为偏应变增量张量;
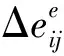

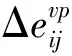
将上述一维本构关系映射到三维条件下,可以分别得到如下本构关系:
(9)
式中K——为体积模量;
F——为屈服函数;
λ〈F〉——为塑性因子增量;
q——为当前应力状态下的广义剪应力:
q1——为当前静水压力和Lode角对应的长期强度。
由于岩石类材料的强度与应力状态相关,不是常数,因此假设长期强度也满足长期强度参数(即长期强度对应的粘聚力c1和内摩擦角φ1)对应的屈服条件(F=0)[1]。仅采用广义剪应力定义稳态粘塑性蠕变的原因是:材料不能被无限压缩,因此静水压力下岩石材料不可能发生稳态蠕变。对于具备强化软化性质的材料,其屈服函数F是应力张量和材料强度参数的函数,材料强度参数是塑性应变的函数,一维情况下为F=τ-τs。式(8)和(9)构成三维条件下的流变模型增量型本构方程。

图3 屈服强度τs与粘塑性剪应变γvp的关系
2 模型的验证及测试
Kelvin体模拟粘弹性蠕变(衰减型蠕变)的效果在众多文献中均有验证,本文不再重复。本节对模型的等速和加速蠕变段模拟效果进行定性测试。将材料粘弹性元件中的弹性元件刚度设为极大值,使其不发生变形,仅考察模型的弹粘塑性变形模拟效果。
对模型进行围压三轴蠕变数值试验,围压恒定为3MPa,施加不同的轴压并保持压力不变,随着时间推进试件从等速蠕变状态过渡到加速蠕变状态,轴压越大,稳态蠕变的速率越大、出现加速蠕变的时间越短,如图4所示。对试件进行围压三轴分级加载蠕变数值试验,当轴压小于长期强度时,轴向应变~时间关系为水平直线,如图5中σ1=20MPa的水
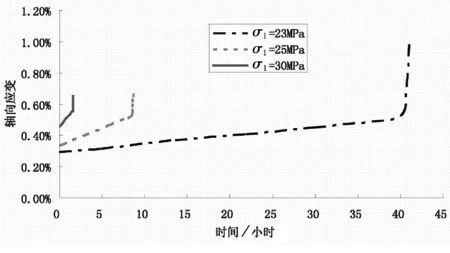
图4 围压三轴蠕变试验的应变~时间曲线(围压3MPa)
平直线段,有瞬时塑性变形发生但没有粘塑性变形发生;当轴压大于长期强度之后,出现等速蠕变现象,蠕变速率随轴压的增大而增大,如图5中轴压等于23MPa的蠕变速率低于轴压等于26MPa的蠕变速率;当加速蠕变条件满足以后,出现加速蠕变现象,试件轴向应变迅速增大,试件破坏,如图5中轴压等于29MPa时,等速蠕变发生一段时间后出现了加速蠕变现象。可见,本文提出的时效本构模型可以有效模拟岩土类材料的完整蠕变三阶段。
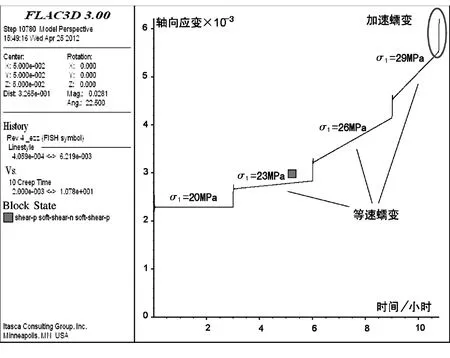
图5 围压三轴分级加载蠕变试验模拟(围压3MPa)
3 模型的工程应用讨论
理论模型应用于工程实际的关键在于模型参数取值的方法。本文提出的时效本构模型除去瞬时塑性变形参数外共有7个参数,分别为:K、G1、G2、η、η2、cl、φl。其中K、G1、G2、η2为Hooke-Kelvin模型的参数,参数的取值可由材料的蠕变试验获得,具体算法可参考文献[14]中所述。参数η为粘塑性粘滞系数,粘塑性变形在蠕变试验中表现为等速蠕变,因此η是应力水平与应变率之比。参数cl、φl是与长期强度q1对应的长期强度参数:
(10)
其取值方法与峰值强度参数c、φ一致,区别在于对应的强度为长期强度。
4 结 语
本文将塑性位势理论与元件流变理论结合,推
导出一个适用于描述围岩破损区演化的时效本构模型,该模型在低应力状态下反映粘弹性性质、高应力状态下反映粘弹—粘塑性性质。与同类型的元件模型相比,本文推导的流变模型只增加了一个长期强度参数(可由力学试验获得),却可以延用塑性位势理论中的屈服条件作为稳态蠕变过渡到加速蠕变的判断准则。因此该模型的意义不仅在于可以较好描述蠕变的三个阶段尤其是确定加速蠕变的起点,更在于统一了岩石瞬时变形破坏与时效变形破坏的破坏准则,两种类型的变形破坏采用同一准则更符合人们对材料破坏准则的定义。
[1] 陈宗基.地下巷道长期稳定性的力学问题[J].岩石力学与工程学报,1982,1(1):1-20.
[2] 孙钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999.
[3] 孙钧.岩石流变力学及其工程应用研究的若干进展[J].岩石力学与工程学报,2007,26(6):1081-1106.
[4] 夏才初,王晓东,许崇邦,张春生.用统一流变力学模型理论辨识流变模型的方法和实例[J].岩石力学与工程学报,2008,27(8):1594-2008.
[5] 龚晓南,袁静,益德清.岩土流变模型研究的现状与展望[J].工程力学,2000,增刊:145-155.
[6] Guan Z,Jiang Y,Tanabashi Y,et al.A new rheological model and its application in mountain tunnelling[J].Tunnelling and Underground Space Technology.2008(23):292-299.
[7] 汪斌,朱杰兵,邬爱清等.锦屏大理岩加、卸载应力路径下力学性质试验研究[J].岩石力学与工程学报,2008,27(10):2138-2145.
[8] 卢允德,葛修润,蒋宇等.大理岩常规三轴压缩全过程试验和本构方程的研究[J].岩石力学与工程学报, 2004, 23(15):2489-2493.
[9] 赵延林,曹平,文有道等.岩石弹黏塑性流变试验和非线性流变模型研究[J].岩石力学与工程学报,2008,27(3):477-486.
[10]徐卫亚,杨圣奇,褚卫江.岩石非线性黏弹塑性流变模型(河海模型)及其应用[J].岩石力学与工程学报,2006,25(3):433-447.
[11]张贵科,徐卫亚.适用于节理岩体的新型黏弹塑性模型研究[J].岩石力学与工程学报,2006,增1:2894-2901.
[12]宋勇平, 雷胜友, 韩铁林. 一种新的岩石非线性黏弹塑性流变模型[J].岩土力学,2012,33(7):2076-2080.
[13]郑颖人,沈珠江,龚晓南.广义塑性力学——岩土塑性力学原理[M].北京:中国建筑工业出版社,2002.
[14]张明,毕忠伟,杨强等.锦屏一级水电站大理岩蠕变试验与流变模型选择[J].岩石力学与工程学报,2010,29(8):1530-1537.

