大岗山拱坝廊道三维静力线弹性有限元分析及配筋方法研究
张元泽,黄志澎,牟高翔,潘艳芳
(1.中国水电顾问集团成都勘测设计研究院有限公司,四川 成都 610072;2.四川大学水利水电学院,四川 成都 610065)
0 前 言
众所周知,混凝土大坝由于泄水、输水、监测、交通、通风等需要,不可避免的在坝体内部设置各种孔洞,如泄水孔、集水井、电梯井、廊道等;孔洞的存在对其周围坝体原有的应力状态有极大的改变,孔洞附近会产生应力集中[1-2],导致局部混凝土开裂破坏。为克服应力集中对大坝结构造成的不利影响,工程中通常采取对孔洞结构进行配筋的方式加以解决。
直接在整体模型上精确模拟坝体孔洞等细部结构需要消耗大量的计算机资源,目前的PC计算机硬件条件尚难以达到;子模型法是获取大型复杂结构局部区域精确解的有限元方法,伴随有限元技术诞生,是工程计算中解决计算机硬件条件不足的有力工具[3]。考虑到坝内孔洞的尺寸与坝体断面尺寸相比很小,孔洞中心距坝体边界的距离较远(大于3倍洞径),文中视这一类问题为小孔口问题,假定孔洞的存在只引起其附近区域应力的局部重分布,对坝体整体的应力分布状态影响较小或无影响,采用子模型法分区域对大岗山拱坝廊道进行了精细化模拟分析。
对拱坝廊道这种大体积混凝土结构的配筋,宜采用按弹性应力图形面积[4]进行配筋的方式。将三维有限元计算成果用于配筋计算,需要将三维应力成果投影到关心的平面(垂直于廊道的横断面)上,目前有限元软件自带的后处理工具无此项功能,国内外也鲜有这方面文件。文中假定每个廊道断面的应力情况由八条特征线(见图7)反映,应用针对ANSYS软件开发的三维插值程序[5],通过三维空间插值及坐标变换从三维有限元计算成果中得到廊道典型断面不同特征线上各点的主应力和环向、轴向的正应力值,接下来对不同特征线处的拉应力进行积分得到相应的拉力值,再运用规范方法得到配筋参数,从而成功的将三维有限元成果运用于大岗山拱坝廊道的配筋计算分析。
1 大岗山拱坝廊道的三维有限元模拟及配筋计算方法
1.1 大岗山拱坝整体模型的模拟方法
大岗山拱坝为混凝土双曲拱坝,坝顶高程1 135m,正常蓄水位1 130m,大坝最低建基面高程 925m,最大坝高 210m;顶拱拱冠处厚10m,拱冠梁底厚52m,厚高比0.248;坝顶中心线弦长525.69m,弦高比2.50。整体模型对主要地质边界及基础处理范围进行了模拟;计算域以坝轴线为中心,向上游约1倍坝高,下游约2.5倍坝高,沿顶拱坝肩向两岸各1.5倍坝高,建基面以下约1倍坝高,顶拱向上取50m,整个范围为1 200m×740m×470m(横河向长度×顺河向长度×高度,下同);整体坐标系的x轴方向垂直河流指向左岸,y轴沿河流方向指向上游,z轴方向为竖直向上。采用solid45单元,坝体采用六面体网格,沿厚度方向分为八层,坝基采用四面体网格;整体模型单元总数58万,节点总数16.4万。拱坝坝体的网格模型见图1,拱坝整体模型网格见图2。整体模型的计算工况选用静力对大坝起控制作用的基本荷载组合I工况,即:正常蓄水位+相应下游尾水位+温降+自重+沙压荷载。

图1 大坝网格模型

图2 拱坝整体有限元网格
1.2 大岗山拱坝廊道的模拟方法
大岗山拱坝廊道系统大致由937m高程排水廊道、基础廊道、979m高程水平廊道、1 030m高程水平廊道、1 081m高程水平廊道、电梯井廊道、支廊道等组成,空间位置关系见图11。若在整体模型上精细化模拟所有廊道,模型要包括几百万个单元及几十万个节点,目前的PC计算机难以实现,因此,采用子模型技术,考虑廊道建模方便将大岗山拱坝廊道分为五个子模型区块(见图3),分别建立各区块包含相应廊道的精细化有限元子模型。以子模型2区为例介绍利用子模型技术模拟大岗山拱坝廊道的过程。

图3 子模型分区示意
子模型2区包括大岗山拱坝坝体11~18号坝段950-1 010m高程范围的基础廊道、水平廊道、支廊道及电梯井等;廊道断面型式为城门洞形式,尺寸分为3m×3.5m、2.5m×3.0m两种。建模时,保持子模型的坐标系和整体模型完全一致,以便于插值运算,子模型的模拟范围为195m×68m×84m;采用自由网格划分方式,单元类型与整体模型保持一致,采用solid45号单元,共有单元665 217个,节点117 194个,有限元网格见图4;为保证各廊道附近区域计算成果的精准度,对相应区域附近的网格进行了加密处理(网格尺寸在0.5m左右,见图5)。
对于子模型2区而言,上、下、左、右四面均为与整体模型切割的边界,因而提取这四个边界上的结点信息,然后利用边界结点信息从整体模型的计算结果中通过插值获取子模型边界上的位移信息,将边界结点处的位移信息读入子模型作为子模型的指定边界条件;接着,利用整个子模型范围的结点信息从整体模型上通过插值提取子模型所有结点对应的温度荷载并添加到子模型中;最后在子模型中施加坝体自重,上、下游水压力,泥沙压力等,以保持整体模型和子模型的荷载条件完全一致。对子模型进行求解分析,即可得到子模型区域的有限元成果。

图4 子模型2区坝体网格

图5 子模型2区廊道有限元网格
1.3 利用拱坝廊道三维有限元计算成果配筋的方法
应用基于ANSYS有限元软件开发的三维插值程序[5],只需要给定廊道断面的四个特征点的(见图6)坐标值,通过三维空间插值和坐标变换,可以得到廊道断面特征线上各点处的应力值,连接特征线上各点应力值得到各特征线方向的截面应力图形(见图7)。沿各特征线上(单宽)对各点拉应力进行积分算出各特征线处的拉应力图形面积,即得各特征线处的拉力值,以8条特征线中拉力值最大者作为断面配筋的依据,根据规范[4],利用式(1)即可求得廊道断面的配筋面积。
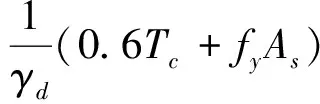
(1)
式中T——截面弹性总拉力;
Tc——混凝土承担的拉力;
fy——钢筋抗拉强度设计值,取310N/mm2;
γd——钢筋混凝土结构系数,取1.20。
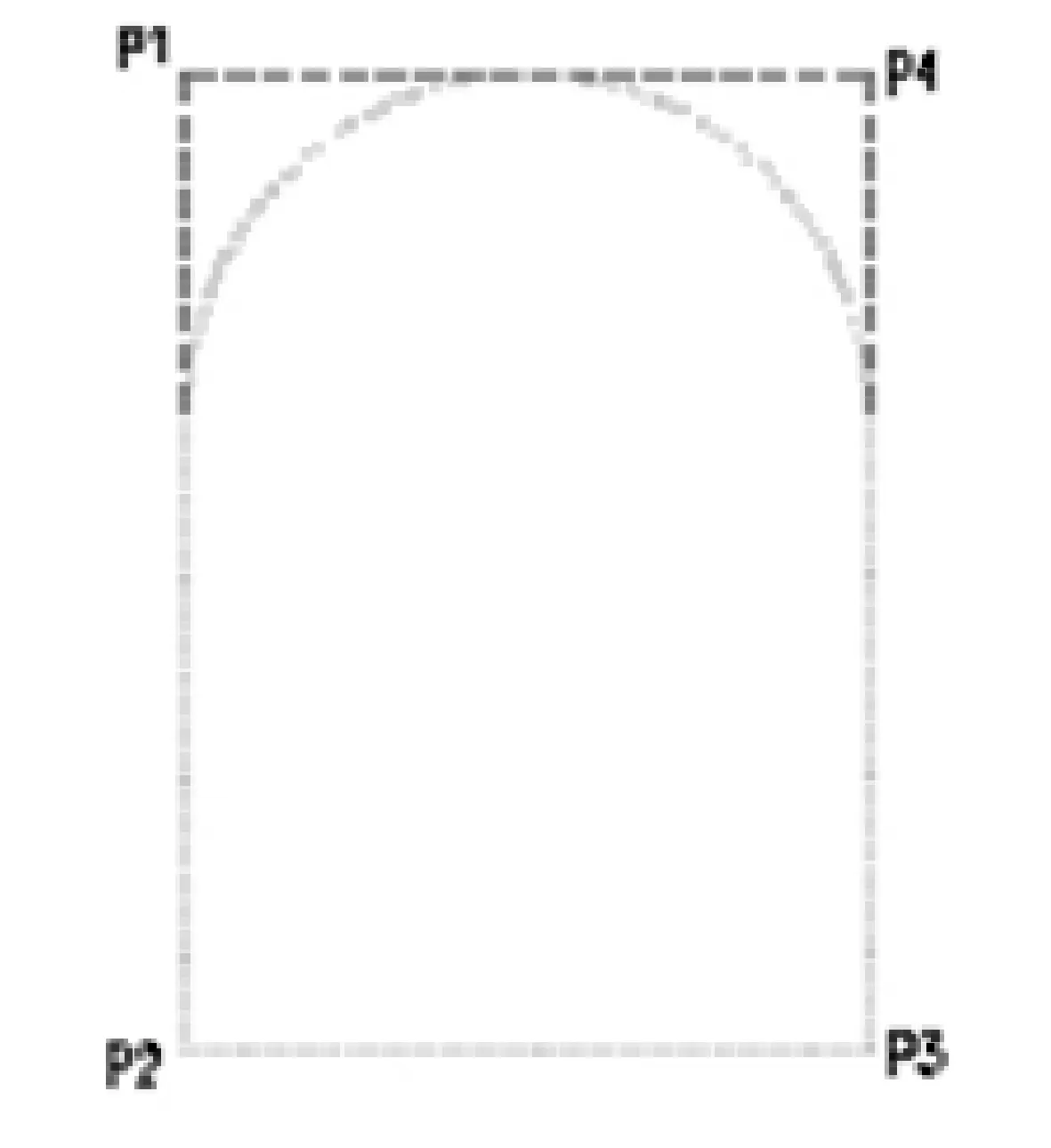
图6 断面控制点示意

图7 轴线为横(顺)河向廊道断面内8个特征线示意
工程实际计算中,从偏安全的角度考虑,将混凝
土承担的拉力完全作为安全储备,认为截面上的拉力全部由钢筋来承担,此时,Tc=0,受拉钢筋截面面积As满足式(2)要求:

(2)
同样以子模型2区为例,从廊道结构图中,选取具有代表性的23个断面(见图8),采用上面的方法,可计算出各个断面处的最大拉力值及配筋面积。

图8 廊道断面位置示意
假定配筋层数为a,钢筋截面积为A1,钢筋间距为d(单位为cm),一延米范围内的配筋满足式(3),通过该式得到各廊道断面的配筋方式。
(3)
2 大岗山拱坝廊道的应力变形特点及配筋参数评价
2.1 大岗山拱坝整体模型与子模型应力变形特点分析
对比分析整体模型与子模型有限元的计算成果,可以得出以下结论:
(1)子模型与整体模型的应力和变形基本一致(见图9~10),由于拱坝左侧建基面地质条件较差,存在较大区域的Ⅲ1类岩体,且下游坝肩处有大量软弱的Ⅳ类、Ⅴ类岩体,弹模较小,左侧的位移比右侧偏大,左侧拉应力区的分布面积也比右侧大。
(2)廊道开孔对其附近的影响范围有限,对一倍洞径范围的影响较大,二倍至三倍洞径范围有轻微影响,三倍洞径以外几乎无影响,表明文中将坝体廊道视为小孔口问题,采用子模型法模拟大岗山坝体廊道的方法合理。

图9 子模型2区与整体模型位移云图对比

图10 子模型2区与整体模型拱冠处断面S1云图对比
(3)横河向廊道的断面,最大主拉应力大致沿第一、第五特征线方向分布,最大主压应力大致沿第三、第七特征线方向分布;顺河向廊道的断面,最大主拉应力大致沿断面的中部特征线两侧分布,最大主压应力沿着第一、五特征线方向分布。
(4)廊道周围环向拉应力较大,轴向拉应力较小。
2.2 大岗山拱坝廊道的配筋参数及评价
运用前文介绍的方法,利用各分区子模型三维有限元计算成果进行配筋计算。计算配筋的原则主要有:
(1)对一倍洞径范围内的主拉应力和正拉应力沿特征线方向单宽(1m)范围分别进行积分,得到每延米范围的配筋面积;
(2)综合考虑工程现场施工、结构所处部位离建基面的距离,拉应力分布等情况,选择以主拉应力或环向正拉应力积分成果作为受力筋配筋,以轴向应力积分成果作为轴向架力筋的配筋;
(3)廊道交叉部位,由于应力情况较复杂,考虑对距离廊道边缘3m范围内进行加强配筋。根据以上原则,给出大岗山廊道受力筋的配筋参数如图11所示,由于轴向拉应力积分成果很小,架力钢筋采用构造配筋,选用Φ25钢筋,层数和间距与受力钢筋相同。
由图11可以看出,采用本文方法配筋能较好的反应高拱坝的受力特点,配筋参数由底部向顶部高程逐渐递减,左岸底部基础廊道(EL.955~966m范围)配筋面积比右侧相应区域略大,靠近建基面配筋面积较大,配筋成果层次清晰明了。
已建的二滩,在建的锦屏一级、溪洛渡和大岗山均为双曲拱坝,尽管坝高不一,但几个工程的拉应力水平相当,分布规律大致相同,因而将几个工程廊道的配筋参数进行对比分析具有重要的意义。表1中列举了几个工程沿高程的配筋面积。

表1 沿高程单宽最大受力筋配筋面积 mm2
注:表中各工程的高程在大坝中的位置相互对应,未反映廊道交叉处周围3m加强配筋。
从表中可以看出,各工程的配筋均比较好的反映了高拱坝应力变化的特点,即:随高程的增加配筋面积减小,基础廊道配筋面积大,水平廊道配筋面积小(锦屏一级1 730m高程附近受地质条件影响较大);锦屏一级、溪洛渡、二滩和大岗山的配筋面积相比,锦屏一级和溪洛渡的坝较高,配筋面积较大,大岗山和二滩的坝高接近,配筋面积也比较接近,可见几个工程的配筋符合一般规律,配筋方案是合适的;大岗山廊道的配筋面积随高程的变化层次明显,与各工程对应高程比配筋量总体最小, 可见采用文中方法配筋是既经济又合理的。
3 结 论
(1)大岗山拱坝整体模型和子模型有限元应力与变形规律基本一致,廊道开孔对其附近的影响范围有限,对一倍洞径范围的影响较大,二倍至三倍洞径范围有轻微影响,三倍洞径以外几乎无影响,表明文中将坝体廊道视为小孔口问题,采用子模型法模拟大岗山拱坝坝体廊道的方法是合理的。
(2)文中以子模型2区为例,介绍了利用子模型技术分区精细化模拟大岗山拱坝廊道,以及将子模型三维有限元计算成果运用于配筋计算的方法,通过和其它已建和在建工程横向对比,表明采用文中方法计算配筋既经济又合理。
(3)文中介绍的大岗山拱坝廊道静力线弹性有限元分析及配筋计算方法经过工程实际运用,取得可喜的经济效益。该方法不仅限于对拱坝廊道的三维有限元分析及配筋,在大体积混凝土结构孔口的分析及配筋方面亦有广泛的推广和运用前景。
[1] 康亚明,杨明成.基于子模型的孔边应力集中的有限元分析[J].湖南工程学院学报,2005,15(4).
[2] 姚瑞平,王磊.孔口应力集中的ANSYS有限元分析[J].江西建材,2012.

