基于近似贝叶斯计算的HMM隐状态估计

陈 琦, 胡锡健

(新疆大学 数学与系统科学学院, 新疆 乌鲁木齐 830046)

隐马尔可夫模型(Hidden Markov Model，HMM)是由Baum L E在20世纪60年代末提出的一个非常重要的统计分析模型，其在语音识别、故障诊断、生物统计等领域中有广泛的应用．评估问题、隐状态估计(解码)问题、参数估计(学习)问题是HMM的三个基本问题.其中，隐状态估计问题在某种程度上其实就是一个贝叶斯估计问题.当HMM的隐状态取连续值时，通常将其称为状态空间模型.对于线性高斯系统，可以利用卡尔曼滤波(Kalman Filter)得到解析解.对于状态空间是离散的、有限的马尔可夫链的系统，运用基于网格的滤波方法(Grid-based methods)可以得到后验概率分布的解析解.但实际上这些条件在很多动态随机系统中很难满足，大部分是非线性、非高斯的，无法求出解析解，因此，只能求助于次优或逼近方法.文献[1]提出扩展卡尔曼滤波(Extended Kalman Filter,EKF),但EKF存在线性化误差，只适用于弱非线性系统.文献[2]提出UT的变换，并在EKF滤波框架里得到广泛应用，被称为UKF，这种方法不必对非线性方程进行线性化和计算雅克比矩阵，均值和方差均可精确到二阶，比标准的EKF精度更高.但由于这两种非线性估计方法都是把pk(xk|y1:k)用高斯逼近，如果真实的分布是非高斯的，那么就不能精确表示状态的真实分布.然而，对于状态空间是连续的但是可以划分成有限的Ns个单元，那么仍然可以用基于网格的逼近方法来近似后验概率密度[3].近年来，将粒子滤波用于处理非线性、非高斯系统的估计，为贝叶斯估计提供了有效的新解法.但当隐状态空间维数很高时离子滤波方法有以下两个不足之处：计算量特别大；不能精确近似目标分布.此外，离子滤波还要求似然函数是逐点可知的，但在实际情况中通常不能满足，而用近似贝叶斯计算方法(Approximate Bayesian Compute,ABC)可以避免这些问题.本文将HMM隐态估计问题看作一个贝叶斯滤波问题，首先详细介绍粒子滤波用于HMM隐状态估计，然后将近似贝叶斯计算思想引入HMM隐状态估计中.

1 问题描述

HMM是一对离散时间随机过程{Xn}n≥1、{Yn}n≥1，其中xn∈dx是隐状态，yn∈dy是观测值。HMM隐状态估计，就是给定观测序列y0:n及模型参数θ，对隐状态作出恰当的判断，即在某种意义下求与此观测序列对应的最优隐状态序列x0:n.这一问题的回答取决于对模型状态物理意义的理解，根据不同的准则，可能会选出不同的最优状态序列．

对∀0≤k≤l及n>0,定义φk:l|n(y0:n，·)为给定Y0:n的条件下Xk:l的条件分布，对于具有转移密度函数的HMM来说，φk:l|n(y0:n，·)是Yn+1到Xl-k+1的转移核，且有密度函数φk:l|n(xk:l|y0:n).对于隐状态估计问题有两种原则，单点最优原则对应于条件分布φk|n(y0:n，·)=φk:k|n(y0:n，·),0≤k≤n；路径最优原则对应于条件分布φ0:n|n(y0:n，·).

单点最优原则下的隐状态估计问题其实是一个最优滤波问题[4]，HMM模型的隐状态是由φk|n(xk|y0:n)而得到的，即时刻k(0≤k≤n)下最有可能的隐状态为

(1)

(2)

2 基于离子滤波的HMM隐状态估计

粒子滤波算法是通过非参数化的蒙特卡洛(MonteCarlo)模拟方法来实现递推的贝叶斯滤波，适用于任何能用状态空间模型描述的非线性系统，其核心思想是得到一批有权重的离散随机采样点(粒子)来近似状态变量的后验概率密度函数，然后利用他们得到估计值，当得到的粒子很多时，其精度可以逼近最优估计.

2.1 离子滤波估计过程描述

HMM隐状态估计的核心是后验分布φ0:n|n(y0:n，·)，假设其密度函数存在，则

(3)

(4)

L(y0:n)φ0:n|n(x0:n|y0:n)=L(y0:n-1)φ0:n-1|n-1(x0:n-1|y0:n-1)q(xn-1,xn)g(xn,yn)

(5)

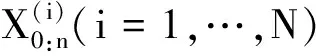
(6)

得φk|n(xk|y0:n)的估计为

(7)

2.2 建议分布选取

故(4)式的最优建议分布为

(8)

2.3 重抽样

在进行序贯重要性采样时，随着 k的增大，将会出现权值退化问题，当n较大时，就将大量的时间浪费在一些对估计结果不起任何作用的粒子更新上，针对权值退化问题，Gordon等提出采用重抽样(Resampling)方法，即评估粒子权值后重抽样粒子以减少小权值的粒子而复制大权值的粒子.

2.4 粒子滤波算法

(a)当k=0时

(b)当k=1,2,…，n时

第k步抽样：

第k步重抽样：

由于

(9)

由(7)式知

(10)

(11)

设

(12)

(13)

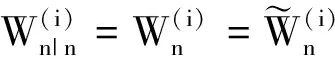
3 基于ABC(Approximate Bayesian Compute)的HMM隐状态估计

3.1 ABC的引入

粒子滤波算法是基于重点抽样来近似目标分布的序列，通常目标分布的维数随着时间参数的增加而增加.在维数很高时，离子滤波有计算量大、不能准确地近似目标分布等缺点.第一个缺点归因于进行模拟和估计权值时的计算量都很大，第二个缺点是由于目标分布本身的复杂性.此外，离子滤波通常要求g(xk,yk)是逐点可得的，但在一些应用中不能满足该要求.采用基于近似贝叶斯计算的方法可以解决此类问题.

近似贝叶斯计算已经成为贝叶斯范例的一个重要方面，在人们感兴趣的许多实际问题中，贝叶斯模型不可得，或者由于计算量太大而不能被拟合，或者所需的模拟方法不能处理问题的复杂性.文献[5]介绍了后验密度π(x|y)∝g(y|x)μ(x)的如下近似：

(14)

其中：Aε,y={u:ρ(s(u),s(y))<ε}；u是一个辅助数据点，∏A是集合A的示性函数，g是似然函数，μ是先验密度，s:dy→ds是一个数据的汇总统计量，ρ是一个距离测度.通常ds比dy小很多.如果s是充分的，可以看到当ε趋于0时，πε(x|y)趋于π(x|y).可以采用拒绝抽样[5]、马尔可夫蒙特卡洛[6]或序贯蒙特卡洛[7-8])等方法对(14)式进行统计推断，其中的关键点是，若不能对g(u|x)进行数值估计，但对任一x，如果可以从g(·|x)进行抽样，仍就可以从πε(x|y)生成样本.

3.2 ABC目标的构建

πn(x1:n|y1:n)的边际ABC目标为

(15)

3.3 ABC目标的SMC算法

第1步：

4 结束语

文中将HMM的隐状态估计问题看成一个贝叶斯估计问题，在单点原则下就是一个最优滤波问题，而解决滤波问题的方法很多，但适用的条件及范围各不相同，其得到的估计结果精度也不相同.离子滤波可以很好地对大部分HMM的隐状态的后验密度进行估计，但其也有自身的一些缺点，并且当遇到g(xk,yk)逐点不可得时，无法对后验密度进行估计.而基于ABC的方法可以对此类情况进行估计，从而使HMM隐状态估计问题得到了全面解决，而且也可以考虑将ABC方法用到其它更广泛的领域中.

[1] Anderson B D,Moore J B.Optimal filtering[M].New Jersey:Prentice-Hall,1979.

[2] Julier S J, Uhlmann J K.A new extension of the Kalman filter to nonlinear systems[C]// The 11th Int Symp on Aerospace:Simulation and Controls. London: 1997:10-12.

[3] 张诗桂，朱立新，赵义正.离子滤波算法研究进展与展望[J].自动化技术与应用 ,2010,29(6):1-16.

[4] 朱成文，李兵，胡奎，等.HMM隐状态的粒子滤波估计[J].计算机工程与应用,2012,48(8):161-167.

[5] Pritchard J K, Seielstad M T, Perez-Lezaun A,etal. Population growth of human Y chromosome microsatellites[J]. Mol Biol Evol.,1999,16, 1 791-1 798.

[6] Majoram P, Molitor J , Plagnol V,etal. Markov chain Monte Carlo without likelihoods[J]. Proc Natl Acad Sci,2003,100, 15 324-15 328.

[7] Beaumont M A, Cornuet J M, Marin J M, et al.Adaptivity for ABC algorithms: the ABC- PMC scheme[J]. Biometrika, 2009,96, 983-990.

[8] Doucet A, Johansen A M. A tutorial on particle filtering and smoothing: fifteen years later[J]. Oxford Handbook of Nonlinear Filtering,2009,7：54-89.

[9] Jasra A ,Singh S S,Martin J S,etal. Filtering via approximate Bayesian computation[J]. Statistics and Computing, 2012,22(6):1 223-1 237.

[10] Moral P D, Doucet A, Jasra A. An adaptive sequential Monte Carlo method for approximate Bayesian computation[J]. Statistics and Computing, 2012,22(5):1 009-1 020.