基于层次分析法采场稳定性评价及FLAC3D模拟验证

肖 超， 郑怀昌， 王 栋， 武文治， 张晓君， 李 明

(山东理工大学 资源与环境工程学院, 山东 淄博255091)

采场稳定性是地下开采的稳定性问题，地下工程的基础是岩体，因此对采场稳定性的研究很大程度上就是对围岩稳定性进行研究，能否正确分出采场围岩稳定性级别决定着采矿方法和地压控制方法.采场围岩稳定性的研究方法有工程类比法、RQD分类法、解析分析法、RMR分类法等，在地下采场围岩稳定分析中也有应用其他理论和方法的,例如有学者采用突变理论、系统观点、关键块体理论以及断裂和损伤力学来分析采场围岩的稳定性[1].文献[2]利用模糊物元分析原理，建立了地下采场稳定性的复合模糊物元评价模型，来帮助决策矿山开采工艺与采场地压控制方法；文献[3]利用模糊物元理论，构造采空区稳定性模糊物元评价模型来较准确评价采空区稳定性；文献[4]通过可靠度对采空区的稳定性进行了分析；文献[5-6]运用模糊综合评价方法综合考虑多种因素建立了评价采空区危险度的评价模型；文献[7]依据石膏矿开采特点，研究使用护顶层厚度﹑顶板厚度﹑采空比等相应技术参数综合评价石膏矿采空区危险度.本文基于层次分析综合评价方法,分析和优选对采空区稳定性程度有重大影响的因素,建立评价模型,预测采场的稳定性情况.

1 筛选指标集

影响采场稳定性的因素是复杂多方面的,我们选取表1所示的3方面因素所包含的11项影响因子作为评价指标集.

表1 评价指标集

2 确定指标权重

2.1 建立层次结构图，构造层次结构模型

层次分析法(Analytic Hierarchy Process，简称AHP)由美国运筹学家、匹茨堡大学教授萨蒂于20世纪70年代初提出，该方法将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础上进行定性和定量分析.利用层次分析法需要确定指标权重，构造的层次结构模型如图1所示.

图 1 采场稳定性评价指标层次结构

2.2 构造两两比较判断矩阵

对于采场稳定性(A)而言，判断采场结构特征因素C1﹑岩体本身因素C2﹑外界干扰因素C3三者的重要性，根据层次分析法的1～9标度(表2),构造出中间层C对于目标层A的判断矩阵(表3).同理,分别构造出指标层A对于中间层C1～C3的判断矩阵 (表4～表6).

表 2 层次分析法的判断矩阵标度

表3 判断矩阵A-C

注：λmax=3.003 7,CI=0.001 8,RI=0.58,CR=0.003 2<0.1

表4 判断矩阵C1-A

注：λmax=3.038 7,CI=0.019 4,RI=0.58,CR=0.033 4<0.1

表5判断矩阵C2-A

注：λmax=3.038 7,CI=0.019 4,RI=0.58,CR=0.033 4<0.1

表6 判断矩阵C3-A

注：λmax=4.987 65，CI=0.017 3，RI=1.33,CR=0.013 4<0.1.

2.3 进行层次单排序，并实施一致性检验方法

根据判断矩阵，对于上一层某元素而言，本层次与之联系的元素重要性次序的权重值的计算过程，称为层次单排序.对于判断矩阵B,计算满足B·W=λmax·W的特征根λmax和特征向量W,W在水平方向上的分量即为相应元素单排序的权重值.一致性检验公式为

CI=(λmax-n)/(n-1);CR=CI/RI

式中:CI为一致性指标;CR为一致性比例;RI为随机性质的指标.当CR< 0.11,视为判断矩阵拥有满意一致性;不然就应该调整判断矩阵,一直到其拥有满意的一致性为止.通过一致性的检验方法可知,表3～表6的判断矩阵均满足CR< 0.11 (部分示例计算得到的结果参见判断矩阵后面注释),拥有令人满意的一致性规律.

2.4 层次总排序及一致性检验

利用获得的每一个因素相对于上一层次对应因素的权重值,统计计算各层次每一元素相对总目标重要作用的排序权值,成为层次总排序，并通过层次总排序计算得到各指标组合权重值 (表7) ,最后利用单排序指标加权求和的方法进行总排序的一致性检验.

表7 基于层次分析得到的结果

3 数值模拟

岩土工程软件FLAC3D能较好模拟出采场开挖及受到流变扰动引起岩石力学性质劣化导致采场稳定性降低情况，以往的层次分析、模糊数学等只结合实例进行了相关探究验证，本文借助FLAC3D软件将数值模拟情况与层次分析理论进行对比验证，探究以上层次分析评价模型是否合理、确定的采场指标权重是否准确.

枣庄市底阁石膏矿区在地质构造上属于鲁西南隆起区南部、韩庄-四户断陷盆地的东部，该地堑呈东西向分布，长达70km左右，宽5～10km，最宽处达15km.矿区内褶皱构造不发育，断裂构造发育.峄城-邵埠大断裂，韩庄-张庄大断裂控制着韩庄-四户地堑的南北边界，地堑内铁佛沟大断裂横贯中部，将该地堑分为两部分，区内地层构成向北倾斜的单斜构造.

根据研究情况，建立的三维计算模型的长、宽、高分别为150m、80m、100m，倾角为8°的石膏层，应用采5留5的方法布置采场，间断矿柱构成房间矿柱，矩形为矿柱的表面积形状，尺寸为5m×5m.每次间隔5个矿房留有隔离矿柱，隔离矿柱尺寸大约为15m左右.计算的模型划分为1 234 891六面体单元网格，相应节点数目为1 378 273.建立的模型如图2所示.约束水平位移被模型侧面边界约束，竖直方向位移被模型底面边界约束，以均布载荷代替采场上覆岩层的重量.考虑石膏的流变特性，采用按比例降低矿柱及其周围岩体强度的方法.

图2 初始采场数值模拟

3.1 采场开挖影响

图3 2个矿房连通时szz分布

石膏层的强度转化为长期强度时，由图3可知，连通矿房附近的矿柱承受的压力明显增大(由正常强度时的4MPa增至14.96MPa)，主要是在尺寸较小非连续矿柱区域；此外，连通部位护顶层局部和护顶层大部分区域受力状态发生改变，即由受压转化为受拉.

由图4可以看出，当连通空间扩至3个矿房时，附近矿柱的受力状态及大小与2个矿房连通时没有发生明显变化,而护底层与护顶层受拉应力的范围明显扩大.

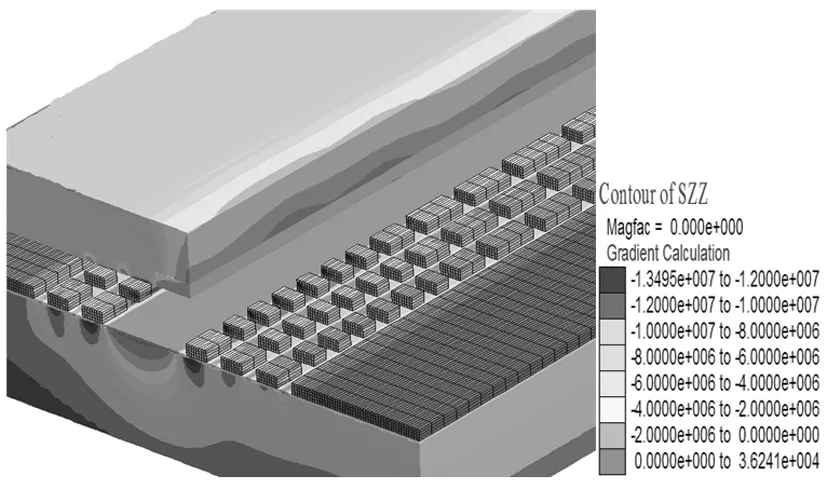
图4 3个矿房连通时szz分布

图5 4个矿房连通时受剪应力影响区域

由图5可以得知，4个矿房连通时有两个方面发生明显变化，一是连通矿房附近矿柱承受的压力值达24.3MPa，接近其强度极限值；二是连通区域附近的矿柱由两侧受剪转为全部受剪，而且边缘应力值达到其抗剪强度值.因此，此时空顶面积在尺寸较小非连续矿柱区域，采空区稳定性达到临界状态，破坏形式为矿柱失稳，护顶层受到拉剪破坏，最终导致大面积采空区冒落.

3.2 采场受到开挖及流变扰动后影响

由图6可以看出，经过长期流变﹑爆破扰动，采场顶板竖向位移变大，顶板及矿柱很多地方处于塑性区，采场顶板已有明显掉渣，矿柱劣化明显，处于比较危险阶段，再继续下去有可能发生大面积冒落，需要进行相应防范措施.

图6 受到开挖及流变扰动的采场数值模拟

经数值模拟验证，观察图2与图3～图6应力大小变化、顶板位移大小变化及塑性区扩大范围，发现岩石强度降低明显，采空区稳定性受到不断破坏，影响采场稳定性的11项影响因素所起作用大小与基于层次分析方法确定的采场稳定指标权重基本吻合.

4 结束语

运用层次分析法 (AHP)确定了采场指标权重，对采场稳定性进行了定量评价，然后运用FLAC3D数值模拟在采空区受到开挖及长期流变、爆破扰动后岩石强度降低情况及采场稳定性降低情况，在分析影响采场稳定性因素所起作用大小时，数值模拟与层次分析结果基本吻合.

[1] 苏龙.基于岩体质量分级的采场稳定性分析与安全对策研究[D].长沙：中南大学, 2012.

[2] 高峰,周科平,胡建华.采场稳定性的模糊物元评价模型及应用研究[J].采矿与安全工程学报, 2006，23(2)：164-168.

[3] 唐硕,罗周全,徐海.基于模糊物元的采空区稳定性评价研究[J].中国安全科学学报, 2012, 22(7): 24-30.

[4] 张晓君.影响采空区稳定性的因素敏感性分析[J].矿业研究与开发, 2006, 26(1): 14-16.

[5] 慎乃齐,杨建伟,郑惜平.基于神经网络的采空塌陷预测[J].煤田地质与勘探, 2001, 29(3): 42-43.

[6] 王新民,段瑜,彭欣.采空区灾害危险度的模糊综合评价 [J].矿业研究与开发, 2005, 25(2): 83-85.

[7] 王新民,丁德强,段瑜.灰色关联分析在地下采空区危险度评价中的应用[J].中国安全生产科学技术, 2006, 2(4): 35-39.