辛普森公式的推广形式及应用

刘智颖， 王向公， 任威龙, 龙耀萍

(1.长江大学 油气资源与勘探技术教育部重点实验室， 湖北 武汉 430100；2.长江大学 地球物理与石油资源学院， 湖北 武汉430100；3.北京吉奥特能源项目责任有限公司， 北京 100195)

当前, 简单而常见的数值积分方法是无限细分法(亦称“黎曼和”).在应用过程中，需将区间划分成尽可能多的份数以保证计算精度.然而，较细的划分会导致计算时间增加，而且当被积函数变化幅度较大时，其误差增大,故辛普森公式应运而生.常见的辛普森公式大都只适用于直角坐标系.事实上很多积分需要在柱坐标和球坐标下进行，如果做坐标变换后再求解则十分繁琐而且会造成误差累积.因此，本文分析、研究并推导了柱坐标系和球坐标系下的辛普森公式，且成功应用于地球物理测井中自然伽马射线强度函数的数值积分运算.

1 三维柱坐标系和球坐标系下辛普森公式的推广

1.1 辛普森公式的常见形式及其适用范围

常见的辛普森公式(公式(1))只能应用于直角坐标系下一元函数的数值积分

(1)

1.2 柱坐标系和球坐标系下的辛普森公式

为书写方便，将柱坐标系下的坐标(ri,θj,zk)及球坐标系下的坐标 (ri,θj,φk)皆记作i,j,k，被积函数在节点处的值记作fi,j,k.脚标i,j,k可以是整数或半整数(其意义与式(1)同).

柱坐标和球坐标剖分体元内插值函数的体积分值有相似的矩阵[2]表达形式(公式2).

(2)

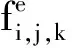
将式(2)中的脚标x替换为i即可得到柱坐标系下的公式.式中矩阵的意义如下：

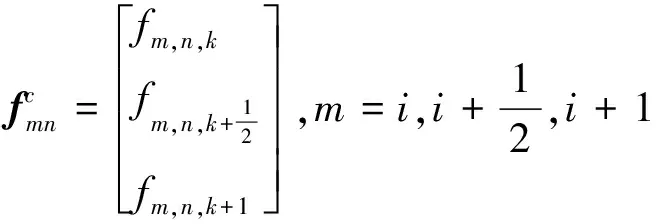
其中A和B两个矩阵只需将Z矩阵中符号zk分别换成θj和ri即可.

将式(2)中的脚标x替换为k即可得到球坐标系下的公式.式中矩阵的意义如下：

其中Φ、Θ和R三个矩阵只要将柱坐标系公式中Z矩阵中的zk分别换成φk、θj和ri即可.

1.3 复化辛普森公式

在实际应用中，由于求解区域的边界不规则，有的节点可能会落到积分区域以外.严格地讲，这时需要对求解区域重新剖分以适应不规则的边界，但一般只要已经满足了精度就可以省去这些繁琐的步骤，只要将落到积分区域以外的节点的函数值设定为零[3]即可.

2 辛普森公式的推广形式在地球物理测井中的应用

自然伽马测井[4]是常见的地球物理测井方法之一.自然伽马射线强度函数值的计算在分析、应用自然伽马测井资料时十分重要，该函数描述了自然伽马测井值(GR值)与地层放射性物质分布情况的关系，需用柱坐标系下的体积分表示.应用辛普森公式的推广形式便可实现对该函数值的计算[5].

通常，为了便于解释人员对相关数据的分析，仪器实测的GR值需要进行“井眼校正”[4].而校正系数是通过计算自然伽马射线强度函数得到的.将不同的井筒直径做为变量输入自然伽马射线强度函数就可以计算出一系列离散的GR井眼校正系数.应用这些离散的数据可以绘制出以井筒直径为横坐标，以GR井眼校正系数为纵坐标的图版(图1).

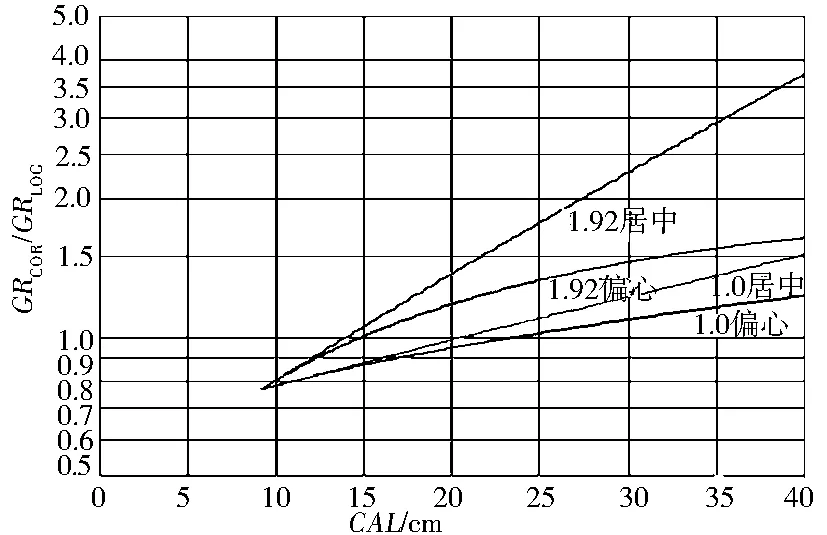
图1 GR井眼校正图版

3 结论和认识

通过分析和总结当前常用数值积分算法的不足，研究数值积分的基本原理，从而推导辛普森公式在三维柱坐标系和球坐标系下的推广形式.对此做出如下总结.

(1)提出并推导了辛普森公式的推广形式，拓展了辛普森公式的适用范围，提高了三维柱坐标系和球坐标系下数值积分的运算速度和精度，弥补了常见数值积分方法的不足.

(2)将辛普森公式的推广形式应用到地球物理测井领域，完成了自然伽马射线强度函数值的计算，从而研制了GR井眼校正图版.

[1] 关治,陆金甫.数值分析基础[M].北京: 高等教育出版社, 1998.

[2] 钱椿林.线性代数[M].3版.北京: 高等教育出版社, 2000.

[3]钱能. C++程序设计教程[M].2版.北京: 清华大学出版社, 2003.

[4]黄隆基.放射性测井原理[M].北京: 石油工业出版社,2000.

[5] 商庆龙.新型自然伽马测井响应的三维数值模拟以及数据合成与高分辨率处理技术[D].吉林：吉林大学，2013：43-56.