Modeling and optimization for molecular weight distribution of polyethylene based on multi-output support vector machine
YE Zhen-cheng,LI Yun,LUO Na
(Key Laboratory of Advanced Control and Optimization for Chemical Processes,Ministry of Education,East China University of Science and Technology,Shanghai 200237,China)
0 Introduction
The molecular weight distribution(MWD)illustrates the relative amount of molecule with different polymerization degree in the polymer,which usually could be formulated by the distribution function[1].The MWD is closely related to the physical properties and processing properties of polymer materials.It’s an important quality index of polymer materials.Therefore,it makes great sense to model and optimize for the MWD[2].
Currently,the rapid real-time detection method for the MWD with good accuracy is uncommon.On the basis of the polymerization reaction mechanism and the combining of moment equation theory and the distribution function,the mechanism model of the MWD can be built.There are several concepts of theoretical analysis about the MWD curves[3-5],but these approaches lead to the different results on the quantity of the separate active centers for the complexity and diversity of the polymerization reaction mechanism[6].It is difficult to describe the MWD with simple and efficient models,which limits the application of mechanism model in practice.Now the research about the MWD is focused on building the hybrid model via the combination of the reaction mechanism and the process data,which is usually realized by the artificial neural network.Chang,etal.presented a neural network rate function (NNRF)approach to model for the MWD[7].Tsen,etal.presented a hybrid neural network model for the MWD[8].Cao,etal.modeled for the MWD based on the B-spline neural network[9].Wu,etal.used the discrete orthogonal polynomial neural network and the recurrent neural network to model for the space and time variables of the MWD[10],and they also used the output feedback method to control the moment of the MWD to realize the tracking of the MWD shape based on the improved neural network model[11].
For the nonlinear system modeling,feed-forward neural network and RBF neural network are the most commonly used methods.Due to the inherent disadvantages,the neural network algorithm tends to fall into local optimum,over-fitting and depending on individual experience in the selection of structure and type[12],which seriously hinders its further application and development.The support vector machine (SVM)algorithm proposed by Vapnik in 1995 has successfully overcome the defects of the neural network algorithm[13],which has exhibited many unique advantages in tackling small sample problems,nonlinear problems,high dimension problems and local minimum points problems,and can be applied to other machine learning problems,such as function fitting problems[14].In recent years,the researches about the theory and application of the support vector machine regression(SVR)algorithm are gradually increasing,but most of them are about single-output problems,only a little are about multiple-output problems.Since solving multiple-output problems with several single-output SVRs would lead to the correlation among the outputs,so it can not treat each sample point fairly.Therefore,the accuracy of the model is poor[15].Pérez-Cruz,etal.in 2002 proposed a multi-output support vector machine(MSVR)algorithm[16].The MSVR algorithm can improve the accuracy of prediction and reduce the computational complexity of the multi-dimensional regression problems.
In this paper,the MWD is fitted by the weighted superposition of the distribution function on each active center of catalyst and the relationship between the process conditions and the parameters of distribution function is described by the MSVR algorithm.The reaction mechanism and the industrial information are merged to build a hybrid model for the MWD.
1 Modeling for the MWD
The polymer MWD is a typical binary modeling object,which could be formulated byMWD(x,p),xdenotes the chain length,pdenotes the parameter.In the past work,the MWD was found to be fitted by the weighted superposition of the distribution function on each active center of catalyst.For linear polymerization reaction of olefin,the MWD usually can be fitted by the Schulz-Flory most probable distribution function,as shown in Eq.(1)[17].Fig.1 has shown the process of the distribution functions fitting the MWD.

wherepi(i=1,…,n)denotes the parameters of distribution function;ndenotes the amount of active centers of catalyst;Mw=1×28.05,2×28.05,…,denotes the molecular weight at a certain chain;M=28.05,denotes the molecular weight of monomer.In Fig.1,αi(i=1,…,n)denotes the corresponding weight.

Fig.1 The fitting diagram for the MWD
According to the research,in the polymer production process with the type of the catalyst identified,the amount of active centers of catalyst and the weight of distribution function are fixed.Therefore the MWD can be represented by the parameters of distribution function on each active center of catalyst,which is decided by the process conditions in the polymerization reaction process.To minimize the fitting error of the MWD,the least squares algorithm is used to obtain the amount of active centers and the weight of distribution function on each active center of catalyst based on the distribution function.The data model built by the MSVR algorithm between the process conditions and the parameters of the distribution function can describe their relationship.Combining the distribution function with the data model,the hybrid model between the process conditions and the MWD is built.
2 The MSVR algorithm
The MSVR algorithm put forward by Pérez-Cruz,etal.in 2002constructs a new loss function — hyper-spherical loss function[16]to replace the traditionalεloss function and introduces the iterated reweighted algorithm to solve the SVM,instead of the quadratic programming algorithm[18].The hyper-spherical loss function can treat all the sample points and fairly treat each of them.
For the multiple-output problem,the authors give a data set{(xi,yi),i=1,…,n},xi∈Rd,yi∈Rq,constructing the nonlinear regression function:
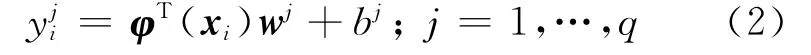

so as to minimize the structural risk:whereyi= (y1iy2i…yqi)T,W= (w1w2…wq)T,B=(b1b2…bq)T.
Eq.(3)has defined aεhyper-spherical insensitive zone,when the norm of error between the actual value and the predicted value is less thanε,and the sample point is inside theεhyper-spherical insensitive zone,the value of the loss function is equal to 0.If the sample point is beyond theεhyper-spherical insensitive zone,the value of loss function would be punished byC.
In order to solve the MSVR,the Lagrange multipliers have been introduced,leading to the minimization:

The solution can be obtained by the KKT conditions:

WhereΦ= (φ(x1) …φ(xn))T,α=(α1…αn)T,yj=(yj1yj2…yjn)T,1 =(1 … 1)T,Dα=diag{α1,…,αn}.


Combining Eq.(5)and Eq.(6),the following equation can be got:Considering the representer theorem:replacingwjwithγj,multiplying Eq.(11)by the pseudo-inverse ofΦDα,and makingH=ΦΦTin Eq.(11),Eq.(13)can be deduced:

According to Eq.(7)-(10),αican be formulated as follows:
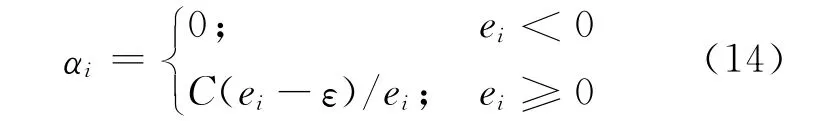
whereei=yi-φT(xi)W-B-ε.
The MSVR procedure can be summarized in the following steps[19]:
(1)Initialization,setγj=0,bj=0(j=1,…,q),and computeei=yi-φT(xi)W-B-ε(i=1,…,n).
(2)Computeαi(i=1,…,n)with Eq.(14).
(3)Computeγj,bj(j=1,…,q)with Eq.(13),and updateei(i=1,…,n).
(4)Ifei≤ε(i=1,…,n),stop,or go back to step(2)until convergence.
3 Optimization for the MWD
In the actual production,according to the utility of the polymer materials,the desired physical properties and processing properties can be counted,and the desired MWDcan be achieved by the theoretical analysis.Optimizing the MWD is to find the suitable process conditionssto make theMWD(s)be closest withThe optimization problem can be formulated as follows:
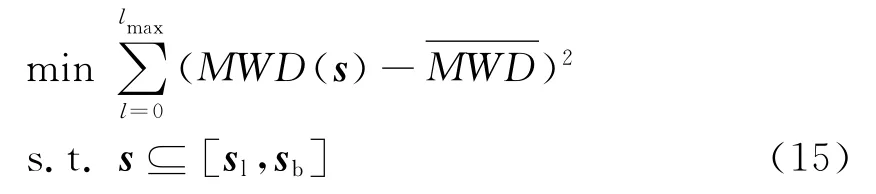
where [sl,sb]denotes the upper and lower bounds of the process conditions[4].
The unconstrained nonlinear optimization method can be used to optimize the problem of Eq.(15).
4 Simulation experiments
Making use of the above methods to model and optimize for the ethylene polymerization process,the main process conditions in ethylene polymerization process are the reaction temperaturet(℃),the reaction pressurep(MPa),the feed rate of ethylenefc(kg/h)and the feed rate of hydrogenfh(kg/h).The process conditions can be represented bys=(tpfcfh).In the case of stable industrial production,the process conditions data of the main reactor can be got from the history database.Meanwhile,the high temperature gel permeation chromatographer can be used to get the MWD data of the polyethylene product in the corresponding condition.Then,in order to minimize the fitting error of the MWD,the least squares algorithm is used to obtain the amount of the active centersnand the parameters of the distribution function in each active center of catalyst based on the distribution function.In this work,the result isn=4and Tab.1has shown some of the parameters of distribution function.For the distribution function,considering that there are few instances where the chain length is greater than 100 000,the chain length has been set among the interval of[1,100 000].With the process conditions in the polyethylenes= (tpfcfh)as input variable,the parameters of the distribution function in each active center of catalystp=(p1…pn)as output variable,the data model can be finished by the MSVR algorithm.An RBF kernel withC=500,σ=4is used in the MSVR algorithm.The experimental results have been shown in Tab.2.

Tab.1 The parameters of the distribution function
The accuracy,mean square error (MSE)and training time are selected to evaluate the results of simulation.The total training time is 0.155 825 s,and the accuracy for each parameter is 1.When the relative error between the predicted value and actual value is under 5%,the forecast result is considered to be accurate,otherwise the result forecast is inaccurate.

Tab.2 The MSE of the MSVR model
With the parameters of the distribution function predicted by the MSVR model,the MWD could be computed by the Eq.(1).Fig.2 has shown the three-dimensional curve of the MWD between the hybrid model and the field data under some specific process conditions.It can be seen that the MWD of hybrid model can track the target MWD well.

Fig.2 The modeling results of the hybrid model
The unconstrained nonlinear optimization method of the Matlab fminsearch function can be used to solve the problem of Eq.(15).Tab.3 has shown the optimization results.It can be found that the optimization results could well match the actual process conditions.

Tab.3 Optimization results
The simulation environment is Core i3-2120 3.30GHz CPU,4.00GB memory,Windows 7 operating system,Matlab 7.8.0 simulation software.
5 Conclusion
In this paper,combining the reaction mechanism and the data model,the hybrid model for the MWD is established.Compared to other hybrid model or mechanism model,this kind of modeling method has the advantages of simple structure,fast calculating speed and more suitability for application in real-time control.Then,the unconstrained nonlinear optimization method of the Matlab fminsearch function is chosen to optimize the process conditions of the MWD based on the hybrid model.The application of these methods in the ethylene polymerization process verifies its feasibility.
[1] Soares J B P,Kim J D,Rempel G L.Analysis and control of the molecular weight and chemical composition distributions of polyolefins made with metallocene and Ziegler-Natta catalysts [J].Industrial &Engineering Chemistry Research,1997,36(4):1144-1150.
[2] GU Xue-ping,WANG Yan-li,CHEN Xi,etal.Optimization of ethylene slurry polymerization conditions based on molecular weight distribution[J].CIESC Journal,2013,64(2):649-655.
[3] Kissin Y V,Mink R I,Nowlin T E.Ethylene polymerization reactions with Ziegler-Natta catalysts.I.Ethylene polymerization kinetics and kinetic mechanism [J].Journal of Polymer Science Part A:Polymer Chemistry,1999,37(23):4255-4272.
[4] Kissin Y V.Molecular weight distributions of linear polymers:Detailed analysis from GPC data [J].Journal of Polymer Science Part A:Polymer Chemistry,1995,33(2):227-237.
[5] Maschio G,Bruni C,Tullio L D,etal.Analysis of the molecular weight distribution (MWD)in polymerization processes:contribution of different families of active sites to the MWD of polyethylene prepared using supported transition metal catalysts[J].Macromolecular Chemistry and Physics,1998,199(3):415-421.
[6] Zakharov V,Matsko M,Echevskaya L,etal.Ethylene polymerization over supported titaniummagnesium catalysts:Heterogeneity of active centers and effect of catalyst composition on the molecular mass distribution of polymer[J].Macromolecular Symposia,2007,260(1):184-188.
[7] Chang Jyh-shyong,Hung Bo-chang.Optimization of batch polymerization reactors using neuralnetwork rate-function models [J].Industrial &Engineering Chemistry Research,2002,41(11):2716-2727.
[8] Tsen A Y,Jang S S,Wong D S H,etal.Predictive control of quality in batch polymerization using hybrid ANN models [J].AIChE Journal,1996,42(2):455-465.
[9] CAO Liu-lin,WU Hai-yan.MWD modeling and control for polymerization via B-spline neural network [J].Journal of Chemical Industry and Engineering,2004,55(5):742-746.
[10] WU Hai-yan,CAO Liu-lin,WANG Jing,etal.Grey box model of polymer molecular weight distribution using hybrid discrete orthogonal polynomial neural network [J].CIESC Journal,2009,60(11):2833-2837.
[11] WU Hai-yan,CAO Liu-lin,WANG Jing.Output feedback control for molecular weight distribution[J].CIESC Journal,2012,63(9):2836-2842.
[12] WANG Ding-cheng,FANG Ting-jian,GAO Li-fu,etal.Support vector machines regression on-line modelling and its application [J].Control and Decision,2003,18(1):89-95.
[13] Vapnik V.The Nature of Statistical Learning Theory[M].New York:Springer,1999.
[14] ZHANG Xue-gong.Introduction to statistical learning theory and support vector machines[J].Acta Automatica Sinica,2000,26(1):32-42.
[15] HU Gen-sheng,DENG Fei-qi.Multi-output support vector regression with piecewise loss function[J].Control Theory &Applications,2007,24(5):711-714.
[16] Pérez-Cruz F,Camps-Valls G,Soria-Olivas E,et al.Multi-dimensional function approximation and regression estimation [C]// Artificial Neural Networks — ICANN 2002.Heidelberg:Springer Berlin Heidelberg,2002:757-762.
[17] Soares J B P,Hamielec A E.Deconvolution of chain-length distributions of linear polymers made by multiple-site-type catalysts[J].Polymer,1995,36(11):2257-2263.
[18] Pérez-Cruz F,Navia-Vázquez A,Alarcón-Diana P L,etal.An IRWLS procedure for SVR [C]//EUSIPCO 2000: European Signal Processing Conference.Tampere:The European Association for Signal Processing,2000:725-728.
[19] Tuia D,Verrelst J,Alonso L,etal.Multioutput support vector regression for remote sensing biophysical parameter estimation [J].IEEE Geoscience and Remote Sensing Letters,2011,8(4):804-808.

