基于粗糙集理论的纸币清分机配置规则获取方法研究
崔文华,孙楚凡,王介生,陈媛媛
(辽宁科技大学 电子与信息工程学院,辽宁 鞍山 114044)
0 引 言
随着我国国民经济进入高速发展阶段,商业活动十分频繁,货币发行量逐年增加,现金特别是纸币的流通量也随之与日俱增,人们对流通货币的质量要求相应有所提高.因此,纸币清分自动化对于金融业来说变得愈发重要.在20世纪90年代中后期出现的纸币清分机是银行系统对于回笼现金货币进行自动清分处理的重要金融机具[1].纸币清分机通过对不同版别、面向、面值和新旧程度的纸币进行快速清分,实现了对流通币、高仿币、变造币、拼凑币的动态鉴伪、自动计数、分类分拣等功能,达到了以智能化机械工具代替传统手工对纸币进行清分、整理的目的,引领银行柜台智能处理终端设备小型化、智能化、模块化、网络化技术发展方向,促进行业科技进步,对维护金融安全具有重大意义.
然而,纸币清分机市场竞争的不断加剧,要求生产企业提供产品快速配置功能,为不同的客户定制出个性化产品.这就需要利用数据挖掘技术对客户的需求进行分析和处理.事实上,在客户表达需求时,通常使用不确定或不精确的语言,如“速度较快”“体积较小”[2],这就与数字化的机器语言产生矛盾.所以采用建立粗糙集知识模型的方法以适应客户的不确定需求.在数据挖掘技术中,粗糙集理论之所以能受到广泛的关注,是因为它可以有效处理数据的模糊性.国内外学者在利用粗糙集处理复杂系统中的数据和信息领域取得了许多成果.文献[3]基于粗糙集理论对信息系统建立决策表,从中获取逆逼近并进行规则提取;文献[4]提出了一种利用粗糙集评价决策成效的方法;文献[5]应用变精度粗糙集方法,采用增量式更新方法对新增决策表进行规则提取;文献[6]提出了一种基于粗糙集理论和支持向量算法的故障诊断方法.
总而言之,解决纸币清分机配置管理的首要问题,是全面、有效地建立和定义产品结构之间的条件属性及决策属性.因此,本文提出采用建立粗糙集知识模型的方法来充分适应客户对纸币清分机的不确定需求.实现上述功能需要建立与产品结构相关联的决策表,利用Skowron差别矩阵进行属性约简及核的提取,建立一种形式化定义配置规则的方法,实现纸币清分机的配置设计.最后,通过实例的配置结果验证所提方法的有效性.
1 纸币清分机概述
1.1 国内外的研究现状和进展
目前,国外企业在清分技术上已经非常成熟,在大、中型纸币清分机核心技术开发上处于领先地位,对于纸币面向、面值的识别率已经接近100%.这使得在大、中型纸币清分机领域,实力雄厚的国外公司占据世界80%以上的市场份额.
近年来,我国逐渐实现纸币清分机的国产化,清分机的自主研发工作取得了突破性进展,在成本控制上具有独特的专利和技术,目前在国内中、小型纸币清分机市场,已经代替进口产品,并且成功走向国际市场.
1.2 纸币清分机工作系统介绍
一个完整的纸币清分机系统主要包括机械导钞系统、传感器系统、控制与显示系统等,如图1所示.纸币清分机清分钞票的流程如下:成叠的被检测纸币由入钞口进入,被摩擦式分钞机构分成单张,通过机械系统传送,完成纸币图像数据的采集;图像处理部分接收到采集数据,进行一系列的算法处理.主控部分按照清分功能对纸币进行辨别,从而实现对纸币的鉴伪.除了常规的荧光、红外、磁性等检测防伪手段以外,有些清分机还具有先进的厚度检测及CIS图像识别功能,可以有效地实现对钞票成色、面向、面额大小、残损度、真伪及变造币的检测和识别,从而实现各种清分功能.

图1 纸币清分机结构示意图Fig.1 Configuration skeleton of currency sorter
2 基于粗糙集的纸币清分机配置规则的获取
2.1 粗糙集理论
粗糙集(rough set,RS)理论是由波兰数学家Pawlak于1982年提出的一种关于数据分析和推理的理论[7].该理论善于从不确定或不精确的数据中获取知识并进行推理,在知识获取、规则生成、智能控制和决策分析等领域应用广泛,特别是在数据挖掘领域,获得了巨大成功.文献[8]对RS理论的基本概念和算法做了比较详尽的阐述.
(1)决策表DT(decision table).称四元组DT={U,C∪D,V,f}是一个决策表,其中
U:U={x1,x2,…,xn},称为论域;
C∪D:C=称为条件属性集,每个αj∈C(1≤j≤m)称为C的一个属性;D=称为决策属性集,且C∩D=,C
V:V=∪Va(a∈C∪D),是信息函数f的值域,其中Va表示值域;
f:f={fa:U→Va,a∈C∪D},是决策表的信息函数,其中fa是属性α的信息函数.
(2)不可分辨关系.给定一个论域U和U上的一簇等价关系S,若P,且P≠,则∩P依然是论域U上的一个等价关系,称为P上的不可分辨关系,记为IND(P),常简记为P.即

(3)集合的下近似和上近似.设U为论域,S是论域U上的等价关系簇,则X和论域U上的一个等价关系R∈IND(K),定义子集X关于知识R的下近似和上近似分别为

(4)知识的约简.设论域上的一簇等价关系PS,对任意的G,若G满足是独立的,且IND(G)=IND(P),则称G是P的一个约简,记为G∈RED(P),其中RED(P)表示P的全体约简组成的集合.
(5)知识的核.设论域上的一簇等价关系PS,对任意的R,若满足IND(P-{R})≠IND(P),则称R为P中必要的,P中所有必要的知识组成的集合称为P的核,记为CORE(P).
(6)决策表的差别矩阵.设DT={U,C∪D,V,f}是一个决策表,其中论域是对象的一个非空有限集合U:U={x1,x2,…,xn},,则定义
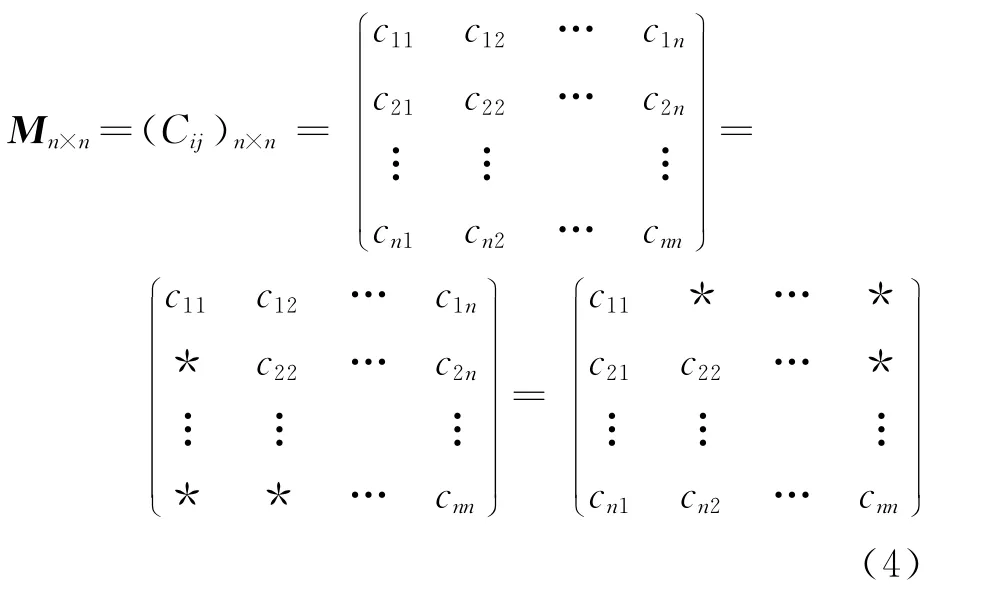
为决策表的差别矩阵,其中i,j=1,2,…,n.
当fD(xi)≠fD(xj)时,
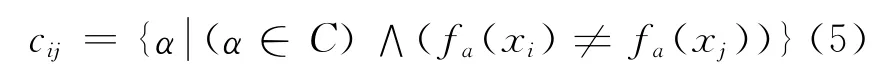
2.2 配置规则的获取
在纸币清分机设计制造的生命周期中,涉及结构、性能等影响因素多种多样.为了满足客户对产品的不同需求,生产企业总是希望能够使客户了解更全面的产品情况,以便提供更加完整的产品配置.但是,企业忽略了客户不是设计者,他们一般不关心“细枝末节”;何况从安全角度考虑,生产企业也不应该将所有设计信息提供给客户.因此,企业可以利用粗糙集理论,获取产品的配置规则,使该规则能适应本企业所掌握的相关产品开发知识,分析开发过程中的各种影响因素,提取关键要素,并总结相关配置,确定适合用户的配置规则,只提供关键要素让用户选择,满足不同客户的个性化需求[9].
对客户的不同需求加以分析,将其分解为相应的知识模型,设定变量和条件;基于产品结构和性能进行个性化配置,形成粗糙集决策表;再进行属性的约简,产生产品的配置结果.纸币清分机的配置设计过程如图2所示.

图2 产品配置设计过程模型Fig.2 Design process model of product configuration
基于粗糙集理论的产品配置的核心思想是通过计算各属性重要度并进行排序,在保证条件属性和决策属性之间相同的依赖关系的前提下找出相关属性的最小集合,用以代替整个属性集合,实现属性信息约简,产生更简洁、更有意义的配置规则.
针对纸币清分机配置规则获取的基本步骤可以概括如下:
步骤1 基于粗糙集理论对纸币清分机进行研究,发现知识模型,分析设计制造过程中影响纸币清分机开发的相关属性,确定在各属性综合影响下纸币清分机的设计结果.
步骤2 将分析得出的相关属性作为原始数据,设定相应的条件属性集合和决策属性集合,选择各属性的值域,并按照规则转换原始数据中相应的数值,建立一个满足粗糙集理论定义的决策表,记为DT={U,C∪D,V,f}.
步骤3 利用Skowron 差别矩阵对决策表进行属性约简及核的提取,写出结果为真的决策规则.
步骤4 删除及合并重复的属性及实例,提取相应的最优配置规则.
3 实例分析
以某品牌的纸币清分机产品为研究对象,就上述配置规则的基本步骤对该产品进行分析和计算.通过实际调查发现,在该品牌纸币清分机产品的生产过程中,用户较为关注的、与产品规则配置相关的关键影响因素主要有尺寸、入钞口容量、出钞口容量、清点速度等.
表1为3 种不同系列的纸币清分机(JL302系列、JL303 系列、JL305 系列)按不同的配置条件得到的实例,决策表中的条件属性(C)包括尺寸(α1)、入钞口容量(α2)、出钞口容量(α3)、清点速度(α4)4项配置要求.决策属性(D)为配置方案,共3个方案.为了体现普遍意义,只使用“大小”“快慢”加以区分,这样使配置结果更加简单、明了,即便客户不具备相关的专业知识,也容易接受.

表1 纸币清分机配置规则Tab.1 Configuration rules of currency sorter
基于粗糙集理论发现纸币清分机的知识模型,将配置决策表抽象化表示,对原配置表进行简化处理,用具体的数字表示其含义[10],结果如表2、3所示.
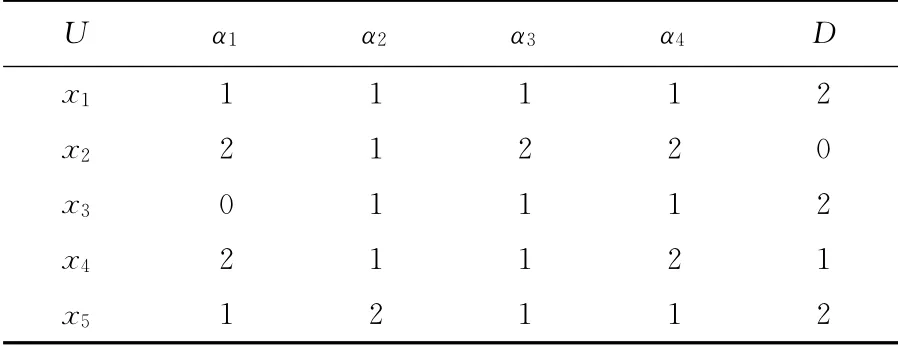
表2 基于粗糙集的纸币清分机知识模型(1)Tab.2 Knowledge model of currency sorter based on RS(1)

表3 基于粗糙集的纸币清分机知识模型(2)Tab.3 Knowledge model of currency sorter based on RS(2)
1991年Skowron首次提出利用差别矩阵来表示知识,这种算法对于知识表达系统中核、约简,以及其他概念的表示和计算具有很多优点.下面采用Skowron差别矩阵来获取该决策表的所有属性约简及核的提取.该决策表的Skowron差别矩阵为

相应的布尔函数的合取范式:

合取范式L∧(∨)转换为析取范式L∨(∧),可得

因此,得到决策表的两个约简为{α1,α3},{α3,α4},核为{α3}.
计算约简后的每一条决策规则的核值,可得简化配置规则表,如表4所示.
简化后的结果对应的决策逻辑为

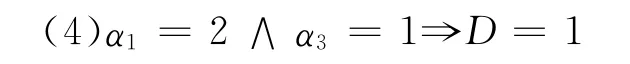
转化为纸币清分机的配置规则为
If(尺寸=一般)or(尺寸=小)then 实例=JL305系列
If(出钞口容量=大)then 实例=JL302系列
If(尺寸=大)and(出钞口容量=一般)then实例=JL303系列
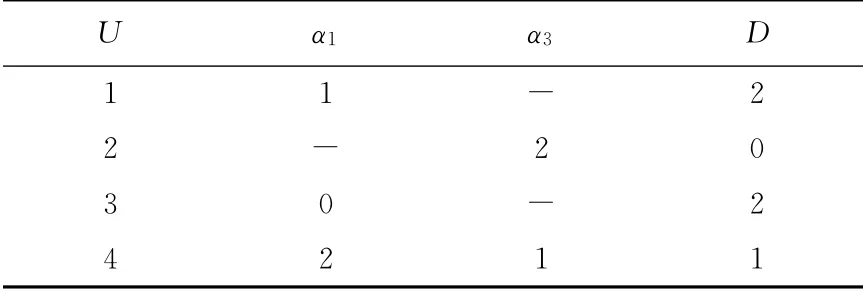
表4 简化配置规则表Tab.4 Reduction of configuration rules
本文基于粗糙集配置规则提取算法容易在计算机上实现,只涉及较少的影响因素,但该算法可以全面地从实例库中不断吸收相关知识.在实际应用过程中,客户需求贯彻整个工作过程.在产品配置乃至整个产品开发过程中,支持随时反馈增加或修改,以满足客户的需求.
4 结 语
纸币清分机作为一种集真伪识别、面额辨别、各种清分功能于一身的现代金融机具,可提高金融行业的分选效率,被多家银行所使用,反馈效果良好.本文在对纸币清分机生产设计过程和历史销售数据分析的基础上,总结出纸币清分机配置规则的获取方法,实现了属性的约简,信息内容得到简化,产生更易于被客户接受的配置规则,具有重要意义.
[1] 何佳兵,李习伦,刘松波,等.纸币清分机系统的研究与开发[J].机电工程技术,2007,36(8):29-31.HE Jia-bing,LI Xi-lun,LIU Song-bo,etal.Research and development on currency sorter system [J].Mechanical & Electrical Engineering Technology,2007,36(8):29-31.(in Chinese)
[2] 车阿大,林志航.产品设计中的获取用户需求的研究及软件系统的开发[J].机械设计,1999(1):20-22.CHE A-da,LIN Zhi-hang.Study and development of software system for-obtaining consumers requirements in product design [J].Machine Design,1999(1):20-22.(in Chinese)
[3] QIAN Yong-hua,LIANG Ji-ye,DANG Chuangyin.Converse approximation and rule extraction from decision tables in rough set theory [J].Computers & Mathematics with Applications,2008,55(8):1754-1765.
[4] QIAN Yu-hua,LIANG Ji-ye,LI De-yu,etal.Measures for evaluating the decision performance of a decision table in rough set theory[J].Information Sciences,2008,178(1):181-202.
[5] 耿秀丽,张在房,褚学宁.基于变精度粗糙集的产品配置规则提取及增量式更新[J].上海交通大学学报,2010,44(7):876-882.GENG Xiu-li,ZHANG Zai-fang,CHU Xue-ning.Research on product configuration rules extraction based on variable precision rough set and incremental updating [J].Journal of Shanghai Jiaotong University,2010,44(7):876-882.(in Chinese)
[6] 舒服华.基于粗糙集与支持向量机的推土机故障诊断[J].筑路机械与施工机械化,2007(1):56-59.SHU Fu-hua.Bulldozer fault diagnosis based on rough set and support vector machine[J].Road Machinery &Construction Mechanization,2007(1):56-59.(in Chinese)
[7] 张文修,吴伟志,梁吉业,等.粗糙集理论与方法[M].北京:科学出版社,2001.ZHANG Wen-xiu,WU Wei-zhi,LIANG Ji-ye,et al.Theory and Method of Rough Set[M].Beijing:Science Press,2001.(in Chinese)
[8] 苗夺谦,李道国.粗糙集理论、算法与应用[M].北京:清华大学出版社,2008.MIAO Duo-qian,LI Dao-guo.Rough Sets Theory,Algorithms and Applications[M].Beijing:Tsinghua University Press,2008.(in Chinese)
[9] 孙国梓,郁鼎文,吴志军.个性化配置器的粗糙集方法研究[J].计算机集成制造系统,2005,11(2):168-172.SUN Guo-zi,YU Ding-wen,WU Zhi-jun.Research on individual configurator based on rough set[J].Computer Integrated Manufacturing Systems,2005,11(2):168-172.(in Chinese)
[10] 高天一,孙 伟,马沁怡.基于粗集理论的产品配置规则获取方法研究[J].计算机工程与应用,2007,43(16):20-21.GAO Tian-yi,SUN Wei,MA Qin-yi.Research on product configuration rules acquirement method based on rough set theory [J].Computer Engineering and Applications,2007,43(16):20-21.(in Chinese)

