基于目标检测和图割的多目标跟踪算法

姜明新，王洪玉，邱天爽

（1.大连理工大学 电子信息与电气工程学部，辽宁 大连 116024；2.大连民族学院 信息与通信工程学院，辽宁 大连 116600）

0 引 言

多目标跟踪是计算机视觉领域的一个热点研究问题，是运动目标行为理解的前提和基础，在机器人导航、视频理解、智能监控等领域都有着广泛的应用［1－3］.多目标跟踪的实现存在很多难点，比如在拥挤的环境里，目标的进入和离开，目标之间的严重遮挡等.

近些年来，国内外许多学者关注基于视频的多目标跟踪问题，所提出的算法包括点跟踪、核跟踪和轮廓跟踪三大类.

点跟踪也称为基于检测的跟踪，利用有效的技术将运动目标检测出来，然后再进行跟踪.跟踪部分的实现可以分为确定性方法和概率方法.确定性方法是利用目标和观测之间某种特征的距离来实现跟踪，特征通常选用位置、颜色、形状等.由于目标检测获得的观测常常含有噪声，概率方法考虑了这些不确定性因素，所以得到了更为普遍的应用，比如卡尔曼滤波［4］、粒子滤波［5］等技术.点跟踪能够处理新目标的进入和原有目标的离开，但检测的质量直接影响跟踪的结果，只能用矩形框、椭圆等来描述跟踪的结果，无法准确地描述出目标的轮廓.

核跟踪也称为基于分布的跟踪，跟踪之前手动选择参考目标，利用当前帧和参考帧的一些特征分布来实现跟踪.较为常见的方法有KLT特征点跟踪算法［6］和 Comaniciu等提出的meanshift跟踪算法［7］.核跟踪计算量小，具有较好的实时性，但无法处理目标的进入和离开，当多目标之间发生遮挡时跟踪的失败率较高.

轮廓跟踪也称为基于动态分割的跟踪，这种方法能够在连续的每一帧中分割多个目标，并且可以描述出每个目标的详细轮廓.利用图割理论［8］实现轮廓跟踪是一种比较有效的方法，这种方法求解全局最小时不需要先获得局部最小和全局模型的先验知识，优化过程收敛快，计算代价低，而且能够处理多个目标相互融合／分离（fusion／split）的拓扑变化.轮廓跟踪的缺点是无法处理新目标的进入和原目标的离开.

通过以上对不同跟踪方法的分析，本文提出一种基于运动目标检测和图割理论的多目标跟踪算法.首先采用码本模型进行背景建模，检测出运动目标；然后，利用图割理论构建网络图，建立能量方程；最后，利用最大流－最小割算法实现能量方程的最小化，进而实现对多目标的跟踪.

1 运动目标检测

码本模型是由Kim 等［9］提出的，该算法抗干扰能力强，能够有效地克服阴影和空洞的问题，计算复杂度小，适合做实时检测.利用文献［9］获得码本后，检测前景似然信息的过程如下：

假设目标检测过程中新输入像素为xi＝（R，G，B），其对应的码本为M.减背景操作BGS（xi）可以大致分为三步：

步骤1 计算当前像素的亮度I＝R＋G＋B，定义布尔变量match＝0，并给阈值变量ε赋值.

步骤2 根据以下两个条件从码本M中找出与当前像素相匹配的码字Cm，如果能够找到码字Cm，则match＝1，否则，match＝0.

为了判断前景和背景，运动目标检测中亮度变化有一个范围，对于每个码字，其范围为［Ilow，Ihi］.亮度函数的定义为

步骤3 判断前景运动目标像素：

2 基于目标检测和图割的多目标跟踪算法

图割是图论中一种关于网络流的算法［10－11］，是一种基于图论的组合优化技术，用来最小化计算机视觉中的能量函数问题.由于网络图相比于向量、表、堆栈等数据结构，具有表示直观、能够处理非线性问题等优点，因此，在计算机视觉领域中被广泛应用.

在多目标跟踪的领域里，可以将监控视频图像映射成一个网络图，建立一个关于目标像素标号的能量函数，通过最大流－最小割算法实现能量函数最小化，求出对应的最小割，从而给不同的像素赋予不同的标签，实现多目标跟踪的目的.由于图割算法是在全局最优的框架下进行分割，可以保证能量函数的解收敛到全局最小.

假设t时刻图像中的像素p用特征向量zt（p）来描述：

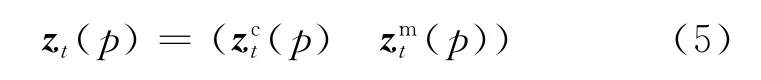
式中：zct（p）表示像素点的颜色信息，是一个YUV颜色空间的三维向量；zmt（p）表示像素点的运动信息，是一个二维的光流向量.

如果在t时刻有kt个目标被跟踪，其中第i个目标用Oit表示，在视频图像中，目标可以看作是多个像素组成的模板.针对目标i来说，视频图像中的像素点不属于该目标，则看作背景，用包含运动信息和颜色信息的概率分布来表示像素点属于目标还是背景.

t时刻属于目标i的像素点的概率分布用lit来表示，对应的特征向量为由于运动信息和颜色信息是相互独立的，lit可以分解为lit，c（对 应的特 征向量 为（对应的特征向量为属于目标i的像素点的概率分布lit的数学表达式为

同理，t时刻属于背景的像素点的概率分布qit（对应的特征向量为可以表示为

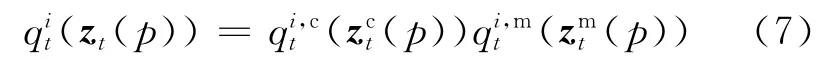
目标跟踪的任务是根据t－1时刻的目标利用图割算法得到t时刻的目标Oit.

如果t时刻共有mt个观测，第j个观测用Mjt表示，Mjt也可以看作是一些像素组成的集合.假设t时刻属于观测j的像素点的概率分布用ρjt来表示，则ρjt的数学表达式为

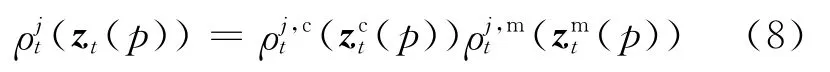
假设由t－1时刻的目标Oit－1预测的t时刻的目标为P，用dit－1表示t－1时刻目标i中所有像素点光流向量的均值，即：

中的每一个像素利用平均光流向量可以预测得到t时刻的目标为：

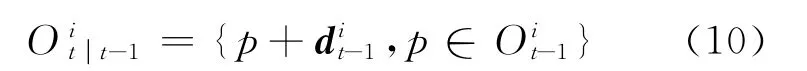
利用t－1时刻的预测、t时刻得到的新的观测值和目标像素的概率分布建立能量方程，通过最大流－最小割算法进行能量函数最小化，实现对多目标的跟踪.基于图割理论的多目标跟踪算法流程图如图1所示.

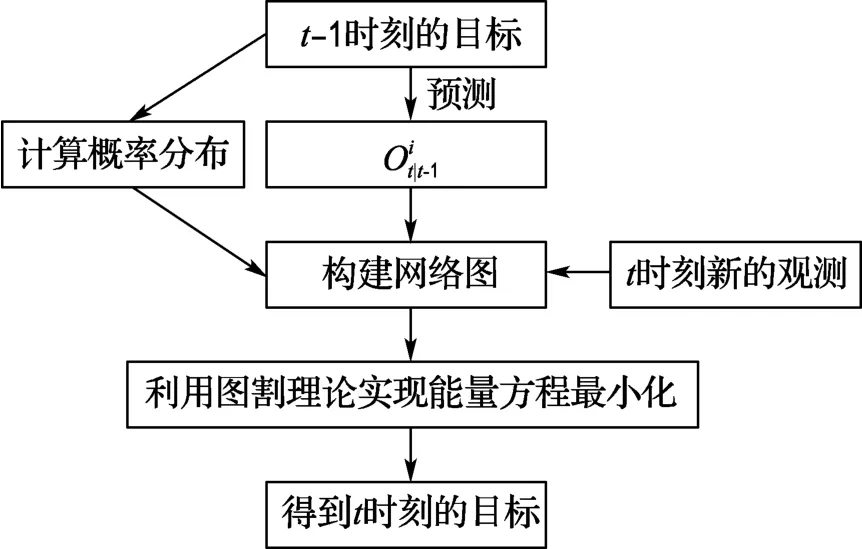
图1 基于图割理论的多目标跟踪算法流程图Fig.1 Flowchart of the multi－target tracking algorithm based on graph cuts

2.1 构建网络图

假设t时刻的无向网络图为Gt＝〈Vt，Et〉，其中Vt为t时刻的点集，Et为t时刻的边集.点集Vt由两个子集组成：第一个子集是N个像素的集合P，第二个子集是观测子集.每一个观测Mjt对应一个节点njt，称这些节点为观测节点，因此，点集Vt＝P∪｛njt，j＝1，2，…，mt｝，边集Et也可以分解 为想要将目标i从视频图像中分割出来，就意味着给图中的每个像素p赋予标签值fip，t，由于针对每一个目标构建一个无向网络图，fip，t对于一个像素点来说不是背景就是目标.想要将观测和目标建立起联系，就意味着给每一个观测节点njt赋予二值标签fij，t.t时刻，所有的节点标签值组成一个标签值集合Lit.

多目标跟踪算法的无向网络图如图2所示.图2（a）表示t－1时刻能量最小化的结果，其中白色节点的标签值为目标，黑色节点的标签值为背景.箭头表示目标的光流向量.图2（b）是t时刻关于目标i的网络图，图中有两个观测节点n1t和n2t，用粗线圈上的像素点分别属于这两个观测.虚线框住的像素点是根据上一时刻目标像素点的光流向量得到的本帧的预测值

2.2 建立能量方程

t时刻，针对目标i建立能量方程，能量方程由一元数据项和二元平滑项组成：

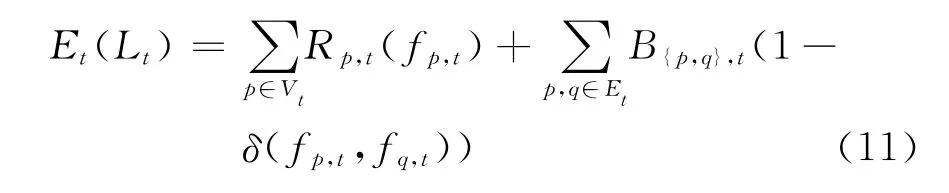
其中数据项为

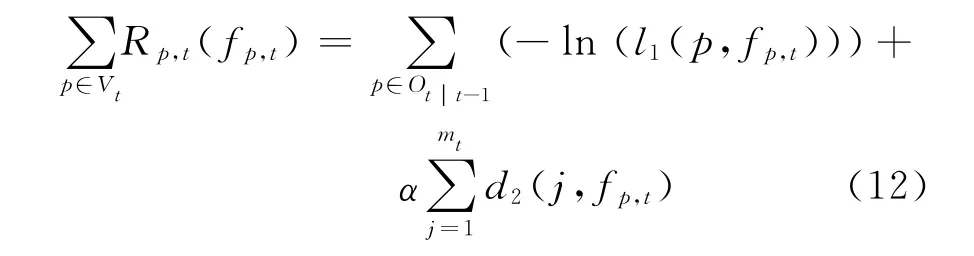
图2 多目标跟踪算法的无向网络图Fig.2 The undirected graph of the multi－target tracking algorithm

式（12）中，利用t－1时刻的跟踪结果得到的t时刻的预测区域的似然函数l1的表达式为

其中“ob”表示像素的标签值为目标，“bg”表示像素的标签值为背景.

式（12）中，d2（j，fp，t）似然函数的数学表达式为

为了估计t－1时刻的目标跟踪结果i和t时刻的.观测j之间的相似度，利用式（14）计算t－1时刻目标i的概率分布lit－1和t时刻观测j的概率分布ρjt之间的距离.本文采用Kullback－Lerbler距离，简称KL距离

式（12）中的常数α是控制观测对数据项的影响程度的，本文中，令α等于观测Mjt的像素数目.

式（11）中的平滑项B｛p，q｝，t的设计基于相邻像素｛p，q｝的颜色梯度信息，具体表达式为

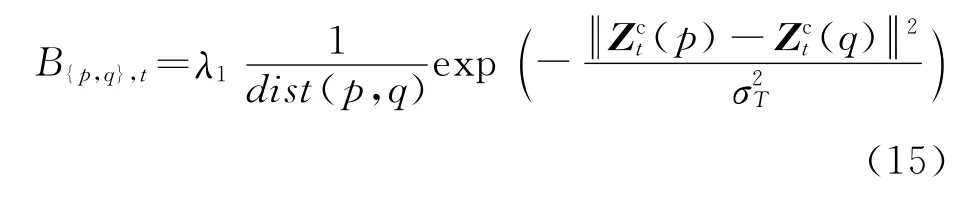
其中σT＝4〈（Zct（p）－Zct（q））2〉，式中的〈·〉表示目标区域的均值.

能量方程式（11）建立后，利用α扩展法进行最小化，求得像素的标签值，可得

则t时刻的目标i为

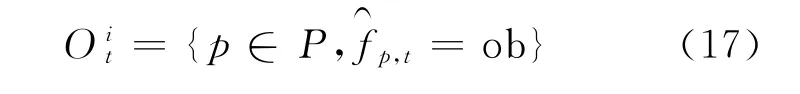
3 实验结果及分析

选用多组实验视频进行测试，验证本文提出的基于目标检测和图割的多目标跟踪算法的鲁棒性，限于篇幅，本文只列出部分实验结果.利用Windows 7操作系统来实现多目标跟踪算法，采用Visual Studio 2010结合OpenCV 2.2作为软件平台，计算机配置为Pentium（R）Dual－Core CPU 2.0GHz.

首先，需要利用运动目标检测算法来获得观测值，实验结果如图3所示.图3（a）和（c）表示监控视频中任意两帧原始视频图像，图3（b）和（d）是利用码本模型获得的观测值.

从图3（d）的结果可以看出，当视频中左侧的两个目标之间发生遮挡时，通过运动目标检测得到的观测是两个目标共同组成的前景.所以，需要考虑预测信息和上一帧目标的概率分布，结合新得到的观测，来共同构建能量方程和网络图.利用图割理论进行多目标跟踪的实验结果如图4所示.

图3 利用码本模型获得的观测值Fig.3 The result of the observation obtained using codebook model

在这组实验视频中，多个目标之间发生了相互遮挡，图4（a）和（b）中目标1和目标3发生了遮挡，图4（c）和（d）中目标1和目标4发生了遮挡，实验视频中的目标4是新进入的目标.

图4 多目标跟踪算法的实验结果Fig.4 The experimental result of the multi－target tracking algorithm

为了更直观地表示给每个像素赋予标签值的效果，将属于同一个目标的像素点赋予了同一种颜色，然后，再用矩形框表示跟踪结果.从实验结果可以看出，提出的多目标跟踪算法，对多目标之间的遮挡和多目标的数目变化具有较强的鲁棒性.

为了验证本文提出算法在跟踪准确率方面的优势，针对上述实验视频进行了跟踪准确率数据统计，并且与粒子滤波算法进行了对比，实验对比数据如表1所示.

表1 跟踪准确率对比Tab.1 The comparison of tracking accuracy

4 结 语

本文在分析各种跟踪方法的基础上，结合点跟踪和轮廓跟踪的优势，提出了一种基于运动目标检测和图割理论的多目标跟踪算法，将多目标跟踪问题转化为能量最小化问题，给像素赋予标签，根据图割理论建立能量方程，构造网络图，利用最大流－最小割算法实现能量方程的最小化，进而完成对多目标的跟踪.实验结果表明，该算法对多目标的数目变化和遮挡具有较强的鲁棒性.

［1］ 姜明新，王洪玉，刘晓凯.基于多相机的多目标跟踪算法［J］.自动化学报，2012，38（4）：497－506.JIANG Ming－xin，WANG Hong－yu，LIU Xiao－kai.A multi－target tracking algorithm based on multiple cameras［J］.Acta Automatica Sinica，2012，38（4）：497－506.（in Chinese）

［2］ Yilmaz A，Javed O，Shah M.Object tracking：A survey［J］.ACM Computing Surveys，2006，38（4）：229－240.

［3］ 姜明新，王洪玉.基于多层定位的多目标跟踪算法［J］.大连理工大学学报，2012，52（5）：767－771.JIANG Ming－xin，WANG Hong－yu.Tracking algorithm of multi－object based on localizing at multiple planes［J］.Journal of Dalian University of Technology，2012，52（5）：767－771.（in Chinese）

［4］ HAN Zhen－jun，JIAO Jian－bin，ZHANG Baochang，etal.Visual object tracking via samplebased adaptive sparse representation ［J］.Pattern Recognition，2011，44（9）：2170－2183.

［5］ Mei X，Ling H.Robust visual tracking and vehicle classification via sparse representation ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33（11）：2259－2272.

［6］ Shi J，Tomasi C.Good features to track ［C］／／Proceedings of the 1994 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Los Alamitos：IEEE，1994.

［7］ Comaniciu D，Ramesh V，Meer P.Kernel－based object tracking［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2003，25（5）：564－577.

［8］ Boykov Y，Veksler O，Zabih R.Fast approximate energy minimization via graph cuts ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2001，23（11）：1222－1239.

［9］ Kim K，Chalidabhongse T H，Harwood D，etal.Real－time foreground－background segmentation using codebook model ［J］.Real－Time Imaging，2005，11（3）：172－185.

［10］ Ford L R，Fulkerson D R.Flows in Networks［M］.New Jersey：Princeton University Press，1962.

［11］ Boykov Y，Kolmogorov V.An experimental comparison of min－cut／max－flow algorithms for energy minimization in vision ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26（9）：1124－1137.