窄通道流动沸腾换热特性实验研究
陈 冲,高璞珍,王 畅
(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001)
近几十年来,随着船舶、电子、航空航天、核能应用等工业的发展,窄通道换热的应用越来越广泛,且越来越受到重视。国内在开发中国先进研究堆(CARR)的过程中,进行了窄矩形通道流动和传热方面的实验和计算验证[1-3]。实验发现,窄通道中的沸腾换热明显高于一般圆管。Ishibashi等[4]在压力低于1.5 MPa的窄通道内饱和沸腾换热的实验研究中表明,窄通道尺寸很小时对沸腾换热有强化作用;沈秀中等[5]通过实验证明,在窄缝环形套管中沸腾产生的气泡,由于受窄缝环形流道几何尺寸的限制,受压变形,在气泡和加热壁面之间过热液膜底层的蒸发使换热大幅受到强化;Lazarek等[6]认为,在窄通道内沸腾换热系数主要依赖于热流密度而不是质量含气率,同时指出泡核沸腾是饱和沸腾传热的主要机理。然而,Lee等[7]认为影响换热系数的因素是质量流速和局部质量含气率,尤其在低流速的情况下,液膜厚度控制着传热效率。
现有的文献多数认为窄通道的沸腾机理主要包括饱和泡核沸腾和两相强制对流,但关于窄通道充分发展沸腾起始点的研究相对较少。本文主要通过窄矩形通道实验来研究影响充分发展沸腾起始(FDB)点的因素及沸腾换热系数的变化趋势,并对充分发展沸腾起始点和换热系数的现有预测模型进行对比。
1 实验
1.1 实验装置
实验装置示于图1。实验段为不锈钢窄矩形通道,采用直流电双面直接加热的方式,实验工质为去离子水。整个实验装置由实验回路和冷却回路组成,实验回路包括实验段、冷凝器、主泵、稳压器、预热器等。其中,长1 000 mm的实验段上非均匀焊接了6组N 型热电偶(从入口到出口,热电偶的间距逐渐减小)用来测量窄矩形通道外壁温的变化,冷却回路主要是对实验工质进行冷却。预热器将实验工质加热到实验段入口所需的温度,主泵提供循环动力,稳压器保证整个回路的系统压力维持在要求的范围内,使整个回路安全可靠地运行。使用电磁体积流量计测量工质的流量,其相对误差在±0.3%以内;压降测量使用两种不同的压力传感器,其量程分别为10kPa和30kPa,其引用相对误差均在±0.2%之内;6组热电偶测量误差在±0.3 ℃以内。

图1 实验装置示意图Fig.1 Scheme of experimental system
1.2 实验参数范围
实验段入口压力为0.1~0.3MPa;入口欠热度为50、40 和30 ℃;入口流量为0.14、0.27、0.41、0.53和0.63m3/h。
2 影响FDB点因素分析
2.1 FDB点位置的确定
在不可视实验段中,FDB点位置主要通过壁面温度的变化来确定。发生过冷沸腾时,由于换热系数升高,会造成沿流动方向壁面温度曲线变平甚至下降,因此可通过寻找壁面温度的转折点来确定FDB 点位置。实验确定FDB点位置主要有两种方法。
1)轴向壁温转折法:根据实验段上热电偶的测量数据,绘制轴向壁温的变化曲线。壁温曲线变平或降低的转折点即为FDB点。
2)单点壁温转折法:在相同的实验工况下逐渐增加功率,绘制单个热电偶处壁温变化曲线,壁温变平或降低的转折点即为FDB点。图2为15 号热电偶处壁面温度随加热功率的变化曲线,当发生气泡脱离时换热系数突然增加,壁面温度突然降低,其幅度约为10 ℃。

图2 壁面温度随加热功率的变化Fig.2 Wall temperature vs.heating power
本实验主要采用第1种方法,第2种方法作为第1种的校验,实验发现这两种方法结果的差别很小。
2.2 热流密度和质量流量对FDB点位置的影响
图3示出入口过冷度为50 ℃时FDB 点位置ZFDB随热流密度和工质流量的变化。由图3可见:FDB 点位置随热流密度的增加逐渐向入口处移动;热流密度保持不变,FDB点位置随工质流量的增加会逐渐远离入口位置,尤其在流量较小(0.14 m3/h)的情况下,FDB点位置随热流密度的增加急剧向入口靠近,然后变化较缓慢,这是因为流量较小时,随着热流密度的增加,工质和壁面升温速率很大,壁面过热度高,易形成汽化核心,从而导致FDB点向入口快速移动,当热流密度达到131kW/m2时,工质温度达到饱和的速度很快,继续增加热流密度对FDB 点位置的影响不大;流量较大时,流体有了一定的热缓冲能力,流体的温度和壁面温度不会急剧增加,FDB点位置向入口缓慢移动。
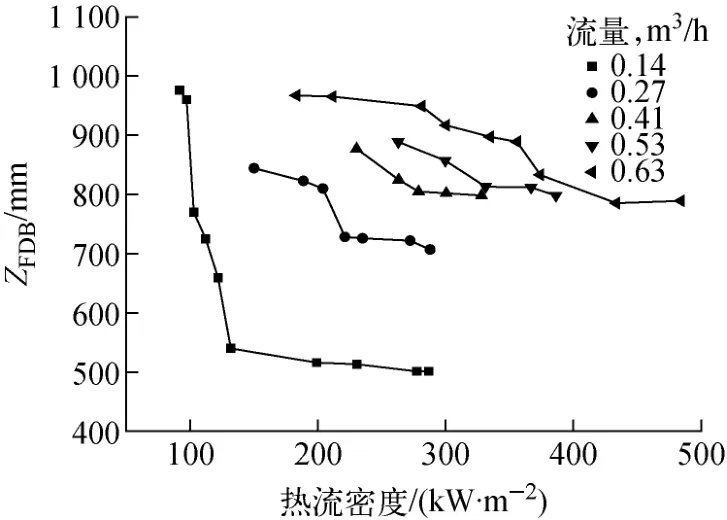
图3 FDB点位置随热流密度和工质流量的变化Fig.3 Position of FDB vs.heat flux and mass flux
2.3 过冷度对FDB点位置的影响
图4示出FDB点位置随热流密度和过冷度的变化。由图4 可见,在相同的热流密度下,随过冷度的增加,FDB点位置会逐渐远离入口位置,因为随着过冷度增加,流体达到泡核沸腾所需的热量增加。但当热流密度达到140kW/m2时,过冷度对FDB点位置的影响变小,因为当热流密度很大时,流体从入口到FDB点位置所需热量的主导控制因素是热流密度,而不是过冷度,因此在高热流密度、不同过冷度工况下,FDB点位置很接近。

图4 FDB点位置随热流密度和入口过冷度的变化Fig.4 Position of FDB vs.heat flux and inlet subcooling
3 FDB 点位置的理论计算值和实验值对比
3.1 理论计算方法
矩形通道的长和宽分别设为a和b,入口质量流量为M,均匀加热,ZFDB处流体的平均温度为tl,Z,流体的入口温度为tl,in,则热平衡方程为:
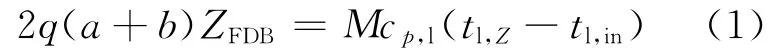
其中:q为热流密度;cp,l为比定压热容。
流体和壁面换热关系式为:
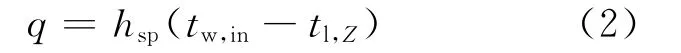
其中:hsp为单相水的换热系数;tw,in为内壁面温度。
由上述两式可得:
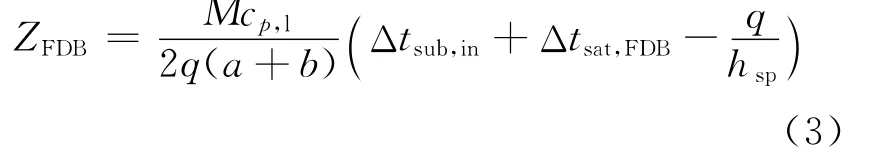
其中:Δtsub,in为液体入口过冷度;Δtsat,FDB为壁面沸腾起始过热度。
3.2 Bowring模型理论值和实验值对比
Bowring[8]的经验关系式为:

其 中:ul,in为 液 体 在 通 道 进 口 处 的 速 度;η 为 经验系数。
Bowring模型提出沸腾起始点是单相对流传热和泡核沸腾传热的过渡点,并将过冷沸腾区分为高欠热过冷沸腾和低欠热过冷沸腾。ZFDB的Bowring模型理论值与实验值对比示于图5。由图5可见,在低热流密度和高热流密度区,理论值与实验值符合较好,其相对误差在±20%以内。
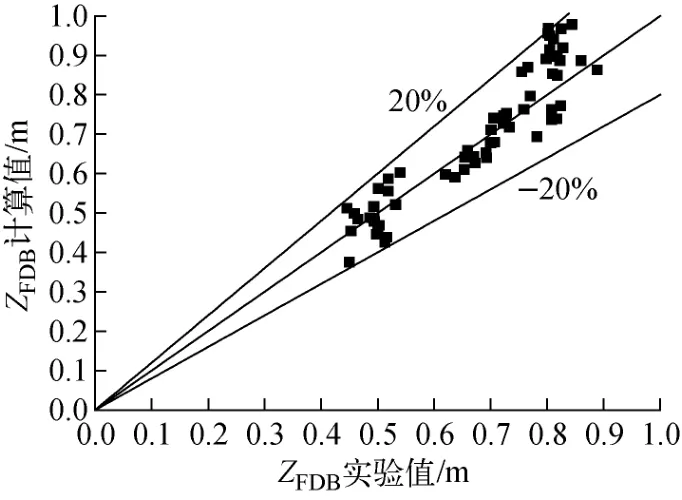
图5 ZFDB的Bowring模型理论值与实验值对比Fig.5 ZFDBcomparison between calculation value by Bowring correlation and experimental data
3.3 Saha-Zuber模型理论值与实验值对比
Saha-Zuber模型[9]为在低流速区,气泡脱离受热力控制,在某一恒定的Nu 下发生过渡;在高流速区,气泡脱离受流体动力效应控制,在某一恒定的St下过渡。Saha-Zuber关系式为:

其中:D 为当量 直 径;λl为 液 相 导 热 系 数;G 为质量流速。
图6示出ZFDB的Saha-Zuber模型理论值与实验值对比。由图6可见,在低热流密度和较低流速的情况下,Saha-Zuber模型的理论值与实验值符合很好,其相对误差在±20%以内。
4 窄通道内的换热系数
4.1 窄通道饱和沸腾换热系数计算方法
窄通道饱和沸腾换热系数计算采用牛顿冷却公式:
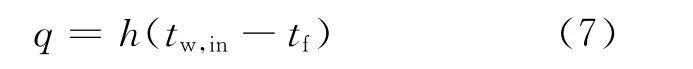
其中,tf为饱和水温度。

图6 ZFDB的Saha-Zuber模型理论值与实验值对比Fig.6 ZFDBcomparison between calculation value by Saha-Zuber correlation and experimental data
实验中测量的是外壁面温度,利用有内热源、一维、平板导热模型的傅里叶公式导出内壁温,图7示出内壁温计算所需要的模型。由傅里叶公式可得:

其中:t为壁面温度;x 为与外壁面距离;φ 为体积释热率;λ为壁面导热系数。

图7 内壁温计算模型Fig.7 Calculation model of inner wall temperature
对上式进行积分得:
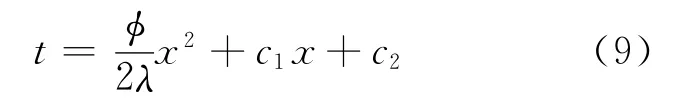
其中,c1、c2为常数。
实验过程中为防止热量从实验段向外散失,在实验段外围增加了保温棉和恒温设备,所以在实验段的外壁面可近似认为是绝热的。
傅里叶公式的边界条件为:
得内壁温与外壁温关系式:

4.2 饱和沸腾换热系数理论值和实验值的对比
1)Chen公式
Chen[10]认为在饱和泡核沸腾区和两相强制对流蒸发区均存在两种基本的换热模式:泡核沸腾换热和强制对流换热,可表示为:
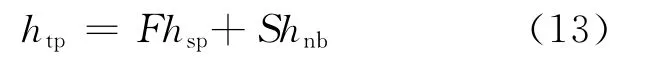
其中:F 为雷诺数增强因子;S 为泡核沸腾抑制因子;hsp为单相对流换热系数,选用Dittus-Boelter关系式计算;hnb为泡核沸腾换热系数,选用Forster-Zuber关系式计算。
2)Gungor-Winterton关系式
Gungor等[11]认为,Chen关系式过度地抑制了泡核沸腾的作用,并认为热流密度在泡核沸腾换热中起重要作用,在此基础上提出Gungor-Winterton关系式,即:

其中,hsp选用Dittus-Boelter关系式计算,hnb选用Copper关系式计算,即:
hnb=55p0.12rq0.67(-0.434 3ln pr)M0.5(15)
其中:pr为折合压力;M 为流体物质的分子质量。
3)Sun Licheng关系式
Sun等[12]认为,矩形通道内的沸腾传热主要受核态沸腾的控制,且通道边界层温度分布的非线性也导致热流密度对沸腾传热系数的影响很大,考虑了Weber数在饱和沸腾中的影响效果,在Lazarek-Black公式的基础上提出一新型的适用于小通道的经验关系式:
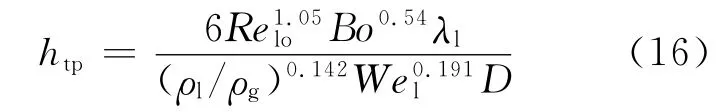
其中:D 为当 量 直 径;ρl、ρg 分 别 为 饱 和 水 和 饱和汽的密度;Wel为韦伯数,定义为:
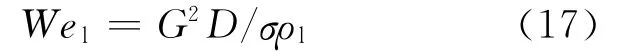
其中,σ为表面张力。
入口温度为80 ℃、流量为0.27m3/h时,沸腾换热系数随平衡态含气率的变化示于图8。由图8可看出,换热系数的计算值和实验值随含气率变化的趋势相同,但用于普通圆管流动沸腾换热的Chen公式和Gungor-Winterton关系式计算窄通道的换热系数和实验值差别较大,尤其在质量含气率较大的区域,这是因为在窄矩形通道内,Chen公式和Gungor-Winterton关系式均过高地估计了强迫对流换热,而窄矩形通道的空间狭窄,气泡的生成和发展受到阻碍。在小流量情况下考虑了矩形通道尺寸效应并认为热流密度在沸腾换热中起重要作用的Sun Licheng关系式与实验值较接近,图9示出Sun Licheng 关系式的误差曲线,其相对误差在±30%以内。
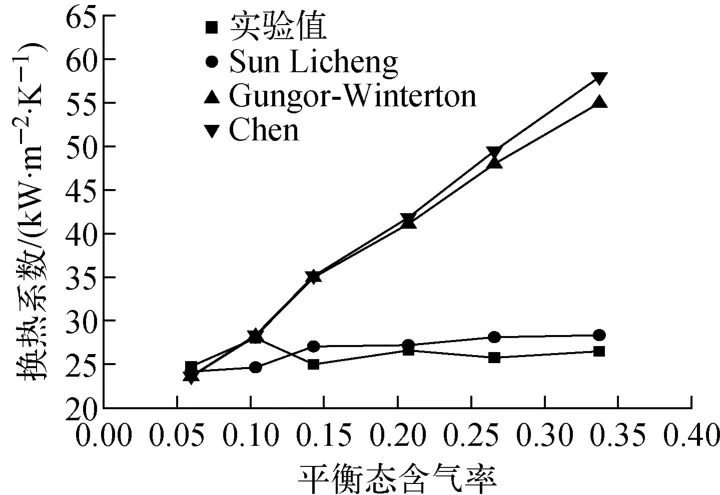
图8 沸腾换热系数随平衡态含气率的变化Fig.8 Boiling heat transfer coefficient vs.thermodynamic equilibrium quality
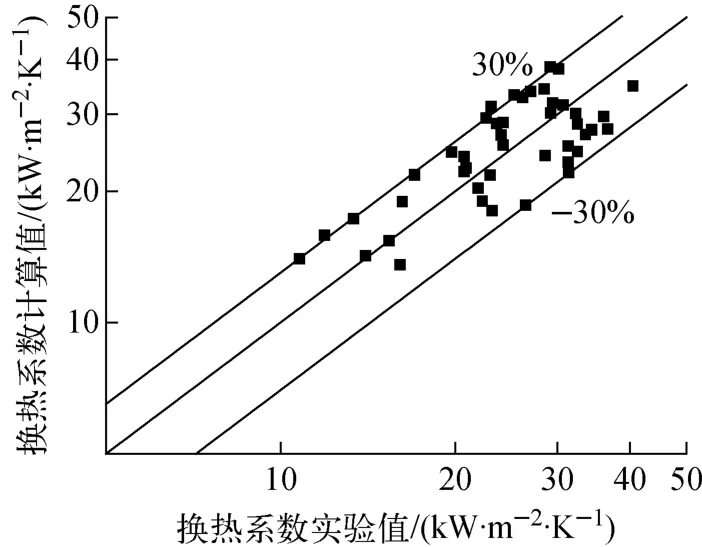
图9 Sun Licheng 关系式的误差曲线Fig.9 Error curve of Sun Licheng correlation
5 结论
在入口压力为0.1~0.3MPa、入口欠热度为30~50℃、入口流量为0.14~0.63m3/h的工况下对400 mm×2 mm 窄矩形通道进行了一系列实验,得出以下结论。
1)随热流密度的增加,FDB点位置逐渐向入口移动,而随过冷度和质量流量的增加,FDB点位置逐渐远离入口,但当热流密度达到140kW/m2时,过冷度对FDB点位置的影响变小,不同过冷度下FDB点位置很接近。
2)在本实验工况下,Bowring模型和Saha-Zuber模型计算的理论值和窄矩形通道实验值的相对误差在±20%以内,可用这两个模型来估算窄矩形通道内FDB点位置。
3)由于窄通道空间狭窄,气泡的行为受到阻碍,使窄通道的换热不同于常规圆管通道,用于常规通道换热计算的Chen公式和Gungor-Winterton关系式不再适用于窄通道的换热计算。而考虑窄通道尺寸效应并认为热流密度在沸腾换热中起重要作用的Sun Licheng关系式在本实验工况下与实验值较接近,其相对误差在±30%以内,可用来估算窄通道沸腾换热系数。
[1] 田文喜,秋穗正,郭赟,等.中国先进研究堆稳态热工水力计算程序开发[J].原子能科学技术,2006,40(1):51-56.TIAN Wenxi,QIU Suizheng,GUO Yun,et al.Development of steady thermal-hydraulic analysis code for China Advanced Research Reactor[J].Atomic Energy Science and Technology,2006,40(1):51-56(in Chinese).
[2] 郎瑞峰.Mechanical Desktop软件在中国先进研究堆堆本体设计中的应用[J].原子能科学技术,2002,36(2):97-100.LANG Ruifeng.The application of Mechanical Desktop in the design of the reactor core structure of China Advanced Research Reactor[J].Atomic Energy Science and Technology,2002,36(2):97-100(in Chinese).
[3] 周涛,张记刚,王若苏,等.中国先进研究堆矩形通道流场数值计算分析[J].原子能科学技术,2009,43(增刊):264-267.ZHOU Tao,ZHANG Jigang,WANG Ruosu,et al.Numerical simulation of temperature and velocity fields in narrow rectangulare channel for China Advanced Research Reactor[J].Atomic Energy Science and Technology,2009,43(Suppl.):264-267(in Chinese).
[4] ISHIBASHI E, NISHIKAWA K.Saturated boiling heat transfer in narrow space[J].Int J Heat Mass Transfer,1969,12(7):863-894.
[5] 沈秀中,宫崎庆次,徐济鋆.在垂直环形窄缝流道中的沸腾换热特性研究[J].核科学与工程,2001,21(3):244-251.SHEN Xiuzhong,MIYAZAKI K,XU Jijun.A study on the flow boiling heat transfer characteristics in narrow inside heating annuli[J].Chinese Journal of Nuclear Science and Engineering,2001,21(3):244-251(in Chinese).
[6] LAZAREK G M,BLACK S H.Evaporative heat transfer pressure drop and critical heat flux in a small vertical tube with R-113[J].Int J Heat Mass Transfer,1982,2(5):945-960.
[7] LEE Hanju,LEE Sangyong.Heat transfer correlation for boiling flows in small rectangular horizontal channels with low aspect ratios[J].Int J Multiphase Flow,2001,27(6):2 043-2 062.
[8] BOWRING R W.Physical model based on bubble detachment and calculation of steam voidage in the subcooled region of heat channel[R].Norway:OECD,1962.
[9] SAHA P,ZUBER N.Point of net vapor generation and vapor void fraction in subcooled boiling[C]∥Proceedings of the 5th International Heat Transfer Conference.Tokyo:[s.n.],1974.
[10]CHEN J C.Correlation for boiling heat transfer to saturated fluids in convective flow[J].ASME Paper,1996,5(3):1-11.
[11]GUNGOR K E,WINTERTON R H S.A general correlation for flow boiling in tubes and annuli[J].Int J Heat Mass Transfer,1986,29(3):351-358.
[12]SUN Licheng,MISHIMA K.An evaluation of prediction methods for saturated flow boiling heat transfer in mini-channels[J].International Journal of Heat and Mass Transfer,2009,52(23-24):5 323-5 329.

