金等离子体M 带谱3d→4f 和3d→5f电子离子碰撞激发强度
杨宁选,张建军,董晨钟
(1.石河子大学理学院物理系,生态物理重点实验室,石河子832000;2.西北师范大学物理与电子工程学院,兰州730070)
1 引 言
金元素其具有较高的X 射线吸收率和转化率,被看作成为惯性约束聚变实验中的理想腔体材料[1-5],因此金元素的辐射特性和在高温下产生的高剥离态离子的碰撞过程在惯性约束聚变及其应用研究中倍受关注.
2000年和2001年,美国Livermore实验室,Glenzer等人[6,7]在惯性约束聚变Au腔靶研究中,用强激光打靶,利用Au激光等离子体M 带谱(金原子M 壳层电了被强激光高度剥离掉一部分后,处在激发态的电了跳回基态辐射的X 光称为M带谱)中5f→3d 和4f→3d 跃迁发射谱和超组态碰撞辐射模型获得了非局域Au等离子体的平均电荷态分布,离子丰度及离子内各能级的布居数.实验结果显示:Au的M 带谱主要由类Ni、类Cu、类Zn和类Ga金等离了体的5f→3d、5p→3d、4f→3d 和4d→3p 等跃迁发射的谱线构成,谱线分布密集不可分辨.而且Au的M 带谱5f→3d 和4f→3d 跃迁谱线很宽,主要由类铁Au52+到类锗Au47+等光谱组成,其中类铜Au50+等邻近离子光谱所占的分额最大.因此研究Au激光等离子体M 带谱5f→3d 和4f→3d 的碰撞过程,对于数值模拟激光X 射线转换效率是很重要的.但是电子与离子碰撞截面的实验测量受到一些客观条件的限制,因此从理论上提供比较精确的碰撞参数显得十分必要.
到目前为止,国内外学者发表了很多有关金离子的跃迁波长、跃迁几率和振子强度等参量的实验和理论研究结果.对于金离子的碰撞激发过程的研究,主要是组态能级之间的电子碰撞激发,例如,理论方面,Zhang等人[8]用相对论扭曲波方法计算过Au51+离子的碰撞强度.Cai等人[9]用准相对论扭曲波方法计算了Au50+离子组态能级之间的电子碰撞激发强度并用最小二乘法拟合了速率系数.Fang等人[10]用准相对论扭曲波方法系统计算了类铜Auq+(q=47~55)组态重心能级之间的电子碰撞强度和速率系数.Yi等人[11]采用准相对论多组态方法和扭曲波波恩交换近似,系统计算了Au等离子体M 带3d→5f 的电子离子碰撞激发速率系数.Zeng等人[12]用FAC 程序系统计算了从Au52+到Au48+离子外壳层电子激发的碰撞强度和有效碰撞强度.实验方面,May等人[13]用电子束离子阱EBIT-I测量了从Au51+到Au48+离子3d→4f 和3d→5f 部分碰撞激发截面,但没有给出详细的数据.
本文利用研究电子-离子(原子)碰撞过程的相对论扭曲波方法和程序包REIE06[14],在系统考虑相对论效应、电子关联效应和Breit相互作用对碰撞强度的影响的基础上,详细计算了Au51+、Au50+和Au49+离子3d→4f 和3d→5f 在不同入射电子能量碰撞时,电子碰撞激发到各精细结构能级间的碰撞强度,计算所得的碰撞参数在超组态碰撞辐射模型中真实模拟非局域热动力学平衡高Z材料Au激光等离了体M 带谱各种复杂离子电荷态分布、离了数布居及激光X 射线转换效率提供有益的帮助.
2 理论方法
具有能量ε的自由电子与靶离子碰撞,使靶离子从初态i 跃迁到末态f 的电子碰撞强度[14-16]Ω(i→f)(ε)可表示为

式中J为碰撞体系的总角动量量子数,κ和κ′分别为入射和散射电子的相对论量子数.为了保证分波的收敛性,本文在碰撞强度(或截面)的计算中选取了κ=50.VBreit是Breit算符[17],Ψiεi和Ψfεf分别是靶离子+连续电子构成的(N+1)电子碰撞体系初、末态的波函数.为了系统考虑连续与束缚电子间的相互作用(包括直接和间接),碰撞体系的波函数采用了(N+1)电子反对称化波函数[14],可表示为
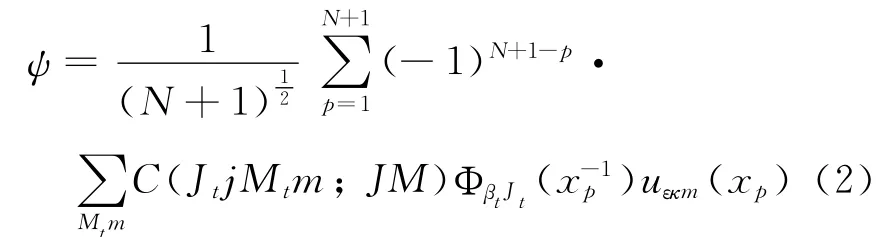
式中,C(JtjMtm;JM)是CG 系数,ΦβtJt是靶离子的波函数,uεκm是连续电子的波函数.
连续电子的波函数采用了相对论的Dirac自旋轨道波函数,可表示为[14]

式中κ是相对论角量子数,Pnκ(r)和Qnκ(r)是径向波函数的大、小分量.目前理论中,对于给定能量的连续电子,其径向波函数的大、小分量可以通过求解耦合Dirac方程而得到.
Breit相互作用对碰撞强度(或截面)的影响,可以通过散射矩阵元的计算中包括Breit算符予以考虑,(1)式中VBreit是Breit算符,表示为[17]

式中r12是两电子间距;和是Dirac矩阵;ω是交换两电子间虚光子的波数.
3 计算结果与讨论
3.1 跃迁能、碰撞强度的比较
采用全相对论Multi-configuration Dirac-Fork(MCDF)理论的程序包Grasp92[18]计算靶离子的波函数,选用扩展平均能级模型(EAL)进行计算,为了考虑组态相互作用对靶离子的波函数的影响,在目前计算中,对于Au51+离子,包括3s23p63d10、3s23p63d9nl、3s23p53d10nl和3s3p63d10nl(n=4、5;l=s、p、d、f)组态间的关联;对于Au50+离子,包括了3s23p63d10nl,3s23p63d94snl,3s23p53d104snl和3s3p63d104snl(n=4,5;l=s、p、d、f)组态间的关联;对于Au49+离子,包括3s23p63d104s2、3s23p63d104snl、3s23p63d94s2nl、3s23p53d104s2nl和3s3p63d104s2nl(n=4、5;l=s、p、d、f)组态间的关联.
离子能级的计算精度,在一定程度上反映了波函数的计算精度,而且影响碰撞激发截面和碰撞强度的计算精度,从表1中可以看出,目前计算的跃迁能与May等人[19]和Seely 等人[20]实验测量结果的最大相对误差不超过1.0%,目前计算的跃迁能与Zeng等人[12]用FAC 程序计算的结果、Shalom 等 人[21]计 算 的 结 果 和Cheng等 人[22]计 算的结果最大相对误差不超过1.0%.
3.2 高离化态Au51+离子3d→4f 和3d→5f 碰撞强度
对于Au51+离子,其基态为3s23p63d10,目前计算了把3l(l=s、p、d)电子激发到nl(n=4、5;l=s、p、d、f)态,共213个精细结构能级的碰撞激发强度.
表2列出了高离化态Au51+离子,其散射电子能量分别是500eV、1000eV、5000eV、10000eV、20000eV 和40000eV 时,3d→4f 精细结构能级间的碰撞强度.对于Au51+离子3d→4f 的碰撞激发,初态为3s23p63d10,末态d 电子(d3/2、d5/2)与f 电 子(f5/2、f7/2)jj 耦 合 产 生20 个 精 细 结 构 能级, 分 别 为 (3d5/24f5/2)0,1,2,3,4,5、(3d5/24f7/2)1,2,3,4,5,6、(3d3/24f5/2)1,2,3,4和 (3d3/24f7/2)2,3,4,5.从表2中可以看出,(3d5/24f5/2)0态的跃迁能最 小 为2473.28eV(3d3/24f5/2)1态 的 跃迁能最大为2604.62eV,两者相差131.3eV;在相同散射电子能量下,从基态到(3d3/24f5/2)1态的碰撞强度最大,并且随散射电子能量的增大,碰撞强度也在增大;从基态到(3d5/24f7/2)1态的碰撞强度也较大,而且随散射电子能量的增大碰撞强度也在增大;从基态到其余精细结构能级的碰撞强度较小,大约要小2个数量级.
对于高离化态Au51+离子3d→5f 的碰撞激发,表3列出了其散射电子能量分别是500eV、1000eV、5000eV、10000eV、20000eV 和40000 eV 时的碰撞强度,同样末态d 电子与f 电子jj耦合产生20 个精细结构能级.从表3 中可以看出,(3d5/25f5/2)0态的跃迁能最小为3351.29eV(3d3/25f5/2)1态的跃迁能最大为3458.43eV,两者相差107.1eV;在相同散射电子能量下,从基态到(3d3/25f5/2)1态和(3d5/25f7/2)1态的碰撞强度较大,并且随散射电子能量的增大,碰撞强度也在增大;从基态到其余精细结构能级的碰撞强度较小,大约要小2~3个数量级.

表1 Au51+,Au50+,Au49+离子跃迁能和碰撞强度的比较,εf表示散射电子能量,△E 表示跃迁能 Table 1 Comparison of the transition energies and collision strengths for Au51+,Au50+,Au49+ionsεf represents the scattered electron energies,△Erepresents the transition energies

表2 高离化态Au51+离子3d→4f 跃迁能和碰撞强度 Table 2 The transition energies and collision strengths of 3d→4ftransition for Au51+ions.500,1000,5000,10000,20000and 40000refer to scattered electron energies,△Erepresents the transition energies

表3 高离化态Au51+离子3d→5f 跃迁能和碰撞强度 Table 3 The transition energies and collision strengths of 3d→5ftransition for Au51+ions.500,1000,5000,10000,20000and 40000refer to scattered electron energies,△Erepresents the transition energies
在相同散射电子能量下,比较从基态到(3d3/24f5/2)1、(3d5/24f7/2)1态 和(3d3/25f5/2)1、(3d5/25f7/2)1态的碰撞强度,可以看出,到(3d3/24f5/2)1态的碰撞强度最大,随散射电子能量的增大,从基态到(3d3/24f5/2)1、(3d5/24f7/2)1态 的 碰 撞 强 度比到(3d3/25f5/2)1、(3d5/25f7/2)1态的碰撞强度增大的趋势更为明显.
3.3 高离化态Au50+离子3d→4f 和3d→5f 碰撞激发强度
对于Au50+离子,其基态为3s23p63d104s,目前计算了把4s和3l(l=s、p、d)电子激发到nl(n=4、5;l=s、p、d、f)态,共405个精细结构能级的碰撞激发强度.
高离化态Au51+离子3d→4f 和3d→5f 的电子碰撞激发,初态为3s23p63d104s,末态d 电子(d3/2、d5/2)、s电子(s1/2)和f 电子(f5/2、f7/2)jj耦合产生39个精细结构能级,以3d→4f 激发为例,其 末 态 为((3d3/24s1/2)24f7/2)11/2,9/2,7/2,5/2,3/2、((3d3/24s1/2)24f5/2)9/2,7/2,5/2,3/2,1/2、((3d3/24s1/2)14f7/2)9/2,7/2,5/2、((3d3/24s1/2)14f5/2)7/2,5/2,3/2、((3d5/24s1/2)34f7/2)13/2,11/2,9/2,7/2,5/2,3/2,1/2、((3d5/24s1/2)34f5/2)11/2,9/2,7/2,5/2,3/2,1/2、((3d5/24s1/2)24f7/2)11/2,9/2,7/2,5/2,3/2和 ((3d5/24s1/2)24f5/2)9/2,7/2,5/2,3/2,1/2.
表4和表5给出了高离化态Au50+离子,其散射电子能量分别是500eV、1000eV、5000eV、10000eV、20000eV 和40000eV 时,3d→4f 和3d→5f 精细结构能级间的碰撞强度.从表4首先可以看出,在3d→4f 碰撞激发中,((3d5/24s1/2)34f5/2)1/2态 的 激 发 能 最 小 为2458.20eV ((3d3/24s1/2)25f5/2)1/2态的激发能最大为2590.86eV,两者相差132.6eV.在相同散射电子能量下,从基态到((3d3/24s1/2)14f5/2)3/2态的碰撞强度最大,并且随散射电子能量的增大,碰撞强度增大的趋势很明 显;从 基 态 到((3d3/24s1/2)24f5/2)1/2态 和((3d5/24s1/2)24f7/2)3/2态的碰撞强度比较大;从基态到((3d5/24s1/2)34f7/2)1/2态 的 碰 撞 强 度 也 较 大,但随散射电子能量的增大,碰撞强度增大的趋势不明显;从基态到其余精细结构能级的碰撞强度较小.
从表5 首先可以看出,在3d→5f 碰撞激发中,((3d5/24s1/2)35f5/2)1/2态 的 激 发 能 最 小 为3316.85eV,((3d3/24s1/2)25f5/2)1/2态的激发能最大为3424.23eV,两者相差107.4eV.在相同散射电子能量下,从基态到((3d3/24s1/2)15f5/2)3/2态和((3d3/24s1/2)25f5/2)1/2态的碰撞强度较大,并且随散射电子能量的增大,碰撞强度增大的趋势比较 明 显、从 基 态 到((3d5/24s1/2)25f7/2)3/2态 和((3d5/24s1/2)35f7/2)1/2态的碰撞强度次之,随散射电子能量的增大,碰撞强度增大的趋势不明显,从基态到其余精细结构能级的碰撞强度较小.
同样比较相同散射电子能量下3d→4f 和3d→5f 碰撞激发强度,可以看出,从基态到((3d3/24s1/2)14f5/2)3/2态的碰撞强度是最大,随散射电子能量的增大,碰撞强度增大的趋势也最明显.
3.4 高离化态Au49+离子3d→4f 和3d→5f 碰撞激发强度
对于Au49+离子,其基态为3s23p63d104s2,目前计算了把4s和3l(l=s、p、d)电子激发到nl(n=4、5;l=s、p、d、f)态,共229个精细结构能级的碰撞激发强度.
高离化态Au49+离子3d→4f 和3d→5f 的电子碰撞激发,初态为3s23p63d104s2,末态d 电子(d3/2、d5/2)和f 电子(f5/2、f7/2)jj耦合产生20个精细结构能级,以3d→4f 激发为例,其末态为(3d5/24f5/2)0,1,2,3,4,5、(3d5/24f7/2)1,2,3,4,5,6、(3d3/24f5/2)1,2,3,4和(3d3/24f7/2)2,3,4,5.
表6和表7给出了高离化态Au50+离子,其散射电子能量分别是500eV、1000eV、5000eV、10000eV、20000eV 和40000eV 时,3d→4f 和3d→5f 精细结构能级间的碰撞强度.在3d→4f碰 撞 激 发 中,(3d5/24f5/2)0态 的 激 发 能 最 小 为2447.20eV,(3d3/24f5/2)1态 的 激 发 能 最 大 为2576.38eV,两者相差约130eV;在3d→5f 碰撞激发中,(3d5/25f5/2)0态的激发能最小为3284.83 eV,(3d3/25f5/2)1态的激发能最大为3390.92eV,两者相差约106eV.在3d→4f 碰撞激发中,在相同 散射 电 子 能 量 下,从 基 态 到(3d3/24f5/2)1态 和(3d5/24f7/2)1态的碰撞强度较大,并且随散射电子能量的增大,碰撞强度也在增大;从基态到其余精细结构能级的碰撞强度较小.在3d→5f 碰撞激发中,在相同散射电子能量下,从基态到(3d3/25f5/2)1态和(3d5/25f7/2)1态的碰撞强度较大,并且随散射电子能量的增大,碰撞强度也在增大;从基态到其余精细结构能级的碰撞强度较小.
在相同散射电子能量下,比较从基态到(3d3/24f5/2)1、(3d5/24f7/2)1态 和(3d3/25f5/2)1、(3d5/25f7/2)1态的碰撞强度,可以看出,到(3d3/24f5/2)1态的碰撞强度最大,随散射电子能量的增大,从基态到(3d3/24f5/2)1、(3d5/24f7/2)1态 的 碰 撞 强 度比到(3d3/25f5/2)1、(3d5/25f7/2)1态 的碰撞 强度增大的趋势更为明显.

表4 高离化态Au50+离子3d→4f 跃迁能和碰撞强度 Table 4 The transition energies and collision strengths of 3d→4ftransition for Au50+ions.500,1000,5000,10000,20000and 40000refer to scattered electron energies,△Erepresents the transition energies

表5 高离化态Au50+离子3d→5f 跃迁能和碰撞强度 Table 5 The transition energies and collision strengths of 3d→5ftransition for Au50+ions.500,1000,5000,10000,20000and 40000refer to scattered electron energies,△Erepresents the transition energies.
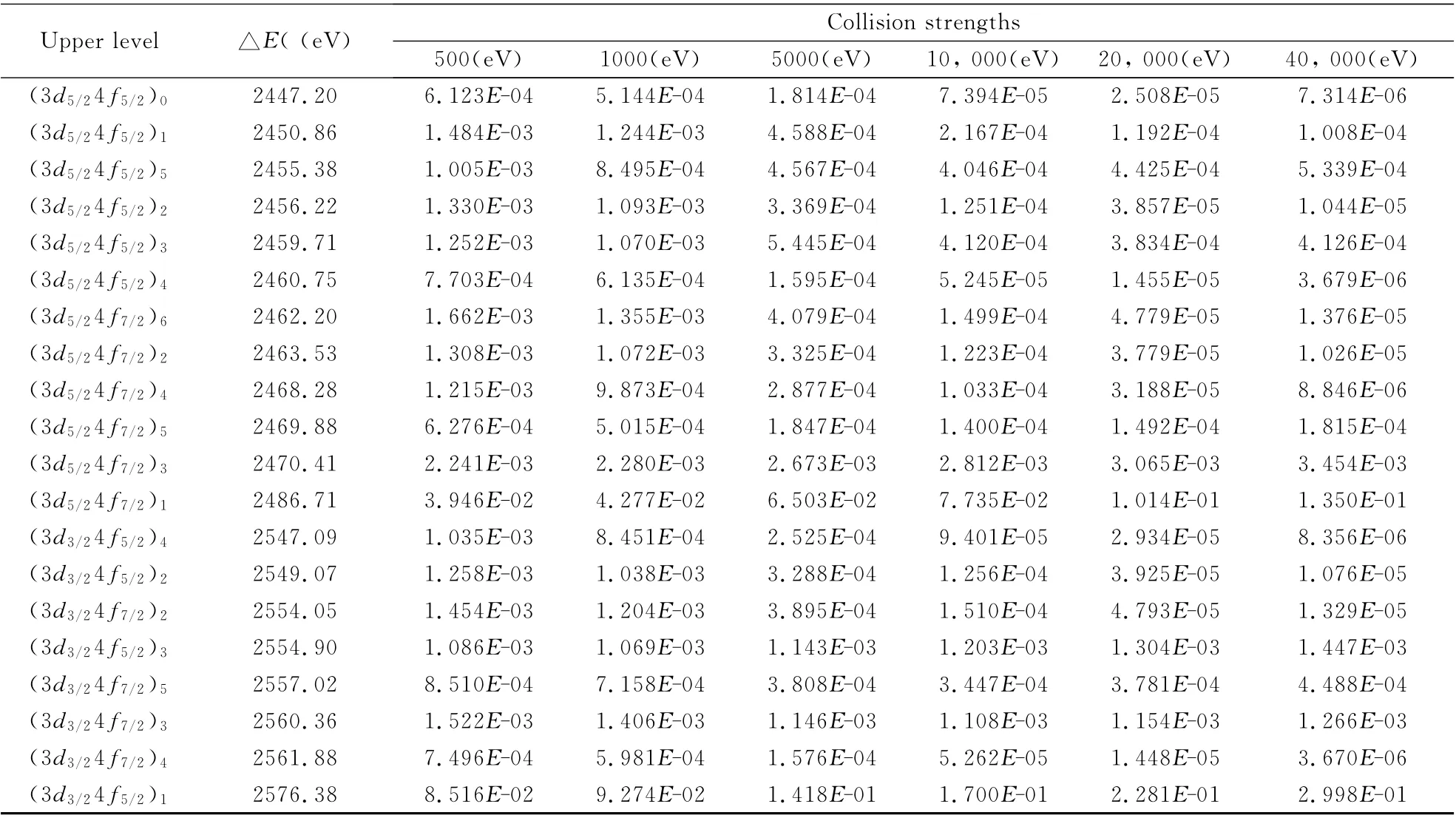
表6 高离化态Au49+离子3d→4f 跃迁能和碰撞强度 Table 6 The transition energies and collision strengths of 3d→4ftransition Au49+ions.500,1000,5000,10000,20000and 40000refer to scattered electron energies,△Erepresents the transition energies

表7 高离化态Au49+离子3d→5f 跃迁能和碰撞强度 Table 7 The transition energies and collision strengths of 3d→5ftransition for Au49+ions.500,1000,5000,10000,20000and 40000refer to scattered electron energies,△Erepresents the transition energies
4 结 论
利用MCDF理论方法和基于全相对论扭曲波方法的研究电子-离子碰撞激发过程的计算程序,详细计算了Au 激光等离子体(Au51+、Au50+和Au49+)M 带谱3d→4f 和3d→5f 各精细结构能级间的碰撞强度,计算中系统的考虑了电子关联和和Breit相互作用,计算结果与可获得的其它理论及实验结果进行了比较,相对误差在10%以内.这些数据在用超组态碰撞辐射(SCROLL)模型模拟Au的激光等离了体M 带谱4f→3d 和5f→3d跃迁的平均电离度、电荷态分布及能级的离了数布居能提供有益的帮助.
[1] Foord M E,Glenzer S H,Thoe R S,et al.Ionization processes and charge-state distribution in a highly ionized high-Z laser-produced plasma [J].Phys.Rev.Lett.,2000,85:992.
[2] Wonk K L,Springer P T,Hammer J H,et al.Spectroscopic characterization of argon-neon Z-Pinch plasma at stagnation[J].Phys.Rev.Lett.,1998,80:2334.
[3] Czerwiec T,Michel H,Bergmann E.Low-pressure high-density plasma Nitriding:mechanisms,technology and results[J].Surface and Coatings Technology,1998,108:182.
[4] Busquet B,Pain D,Bauche J,et al.Study of X-ray spectrum of laser-produced gold plasmas[J].Phys.Scr.,1985,31:137.
[5] Tragin N,Geindre J P,Minier P,et al.Extended analysis of the X-ray spectra of laser-irradiated elements in the sequence from tantalum to lead[J].Phys.Scr.,1988,37:72.
[6] Glenzer S H,Wilson B G,Fournier K B,et al.Ionization balance in the inertial confinement fusion hohlraum plasmas[J].Journal of Quantitative Spectoroscopy &Radiative Transfer,2001,71:355.
[7] Forrd M E,Glenzer S H,Thoe R S,et al.Accurate determination of the charge state distribution in well characterized highly ionized Au plasma[J].J.Quant.Spectorosc.Rad.Trans.,2000,65:231.
[8] Zhang H L,Sampson D H,Fontes C J.Relativistic distorted-wave collision strengths and oscillator strengths for the Ni-like ions with 60 ≤Z≤92[J].Atomic Data and Nuclear Data Tables,1991,48:91.
[9] Cai W,Fang Q Y,Zou Y,et al.Excitation collision parameters and scaled rules of Cu-like ions by electron impact[J].High Power Laser and Particle Beams,1997,9(5):199.
[10] Fang Q Y,Cai W,Zou Y,et al.Excitation collision strength and rate coefficient of Auq+(q=47,55)ions by electron impact[J].J.Quant.Spectorosc.Rad.Trans.,1999,62:59.
[11] Yi Y G,Zheng Z J,Yan J,et al.Collision excitation rate coefficients by electron impact in a highly ionized Au plasma [J].High Power Laser and Particle Beams,2003,15(2):145.
[12] Zeng J L,Zhao G,Yuan J M.Electron impact collision strengths and oscillator strengths for Ge-,Ga-,Zn-,Cu-,Ni-,and Co-like Au ions[J].Atomic Data and Nuclear Data Tables,2007,93:199.
[13] May M J,Beiersdorfer P,Jordan N,et al.Measurement of electron impact collisional excitation cross sections of Ni to Ga-Like Gold [J].Nucl.Instrum.Methods Phys.Res.B,2005,235:231.
[14] Jiang J,Dong C Z,Xie L Y,et al.Relativistic distorted-wave calculations of electron impact excitation cross sections of Be-Like C2+ions[J].Chin.Phys.Lett.,2007,24:691.
[15] Christopher J F,Sampson D H,Zhang H L.Inclusion of the generalized Breit interaction in excitation of highly charged ions by electron impact[J].Phys.Rev.A,1993,47:1009.
[16] Zhang H L,Douglas H S.Procedures for improving a relativistic distorted-wave approach for excitation of ions by electron impact[J].Phys.Rev.A,1993,47:208.
[17] Dong C Z,Fritzsche S.Relativistic,relaxation,and correlation effects in spectra of CuⅡ[J].Phys.Rev.A,2005,72:012507.
[18] Parpia F A,Fischer C F,Grant I P,et al.GRASP92:apackage for large-scale relativistic atomic structure calculations[J].Comput.Phys.Commun.,1996,94:249.
[19] May M J,Fournier K B,Beiersdorfer P,et al.X-ray spectral measurements and collisional radiative modeling of Ni-to Kr-like Au ions in electron beam ion trap plasmas[J].Phys.Rev.E,2003,68:036402.
[20] Seely J F,Ekberg J O,Borown C M.Laser-produced spectra and QED effects for Fe-,Co-,Cu-,and Zn-like ions of Au,Pb,Bi,Th,and U [J].Phys.Rev.Lett.,1986,57:2924.
[21] Bar-shalom A,Oreg J,Klapisch M.The effect of the configuration interaction on relativistic transition arrays[J].Journal of Quantitative Spectroscopy and Radiatve Transfer,2000,65:415.
[22] Cheng K T,Robert A W.Quantum electrodynamics effects in the 4s-4p transitions in Cu-like and Zn-like ions[J].Phys.Rev.A,1987,36:5453.

