监测过程均值小的偏移的综合控制图

宋向东， 宋宗伟

(燕山大学 理学院 河北秦皇岛066004)

0 引言

为了进一步监测过程均值小的偏移，文献［1］提出了一个结合休哈特控制图以及合格品链长控制图(CRL控制图)的综合控制图(通过把样本组作为一个单元)，在此基础上文献［2］又提出一种“group runs”控制图．本文与之前研究不同之处是在随后的运行当中出现CRL值小于等于L时，认为控制图处于警戒状态，紧接着做下一轮单元组检验，这时采取增加单元组的样本量．如果检验的CRL值小于等于L，即为第一次出现两个连续的CRL值小于等于L，就认为过程失控［3］．让μ0代表过程受控下的均值，ARL(δ)代表均值由μ0偏移到μ0±δσ时从而发出报警信号的平均链长．对于休哈特控制图来说，其中β为第2类型错误，n为样本量，k为控制限系数，ARL(0)基于错误报警概率的原因经常被使用者明确指定．

1 合格品链长控制图

在百分百检验当中，合格品链长控制图是为了检验两个不合格单元组之间所检验的单元组的个数(包括最后一个不合格品单元)．从图1中可以看出CRL1=4，CRL2=5，CRL3=3．

图1 合格品链长控制图的图形解释Fig．1 Control chart explanation of conforming run length

在休哈特控制图中，如果样本均值没有落在控制域内则认为失控，VGR控制图会认为该样本单元组不合格．已知，令ATSCRL代表检验单元组的平均数，即

2 VGR图的设计与执行

2．1 VGR图的概念

1)μ0:受控下的过程均值．

2)σ:过程标准差．

3)ATS(δ):当过程均值由μ0偏移到μ0±δσ时从而发出失控信号的平均时间．

4)δ1:均值的偏移量，其大小被认为是大到足以严重影响产品的质量．

5)n:样本单元组的数目．

6)k:子图的控制限系数．

7)L:VGR图的下限．

8)Yr:第r－1个与第r个不合格单元组间的单元组数．

2．2 VGR图的设计

VGR(n1，n2，k，L，delta)是结合可变样本、休哈特控制图以及合格品链长控制图用来监测均值小的偏移的控制图［4］．它有一条单一的线Y=L，VGR图的运行如下:

1)连续的检查含有n1个样本的单元组，把每个单元组看作一个个体．

3)如果Y1≤L认为过程失控或出现一个Yr≤L(Yr≠Y1)，紧接着检查含有n2个样本的单元组，同时Yr+1≤L也认为过程失控．如果该Yr+1＞L就认为受控，将要返回第1)步继续进行．

4)当过程失控时，就需要采取相应的纠正措施重新设置，返回到第一步重新开始．

以上过程可以通过流程图2加以解释．K=2代表处于失控状态，从而发出失控信号，应及时对产品采取纠正措施．

令P为不合格品单元组的概率，

令Yr(r=1，2，…)为独立同分布服从几何分布的随机变量，它表示第r－1个与第r个不合格单元组之间的单元组数，令N代表过程失控时检验的不合格单元组的个数．检查样本量为n1的单元组时Yr≤L的概率为

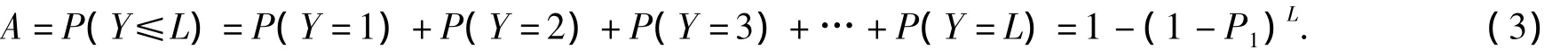
同样，检查样本量为n2的单元组时Yr≤L的概率为B=1－(1－P2)L．

当 r=1，P(N=1)=P(Y1≤L)=A;当 r=2，P(N=2)=0;

当 r≥3，P(N=r)=(P(Yr≤L)P(Yr－1≤L)P(Y1r－2＞L))P(N＞r－3)+(P(Yr≤L)P(Yr－1≤L)P(Y2r－2＞L)P(Y1r－3＜L))P(N ＞r－4)．

首先定义一个函数ATS，它是当过程发出失控信号时要检验的所有样本量的平均数．即ATS=n1·ARL1+n2·ARL2．其中ARL1表示信号发出后已检验的样本量为n1的单元组的平均数．ARL2表示信号发出后已检验的样本量为n2的单元组的平均数．

品监测流程图

t monitoring flow chart

当单元组的样本量为n1时，判断该单元组是否合格的区间为

K=0表示为开始的状态;K=1表示有一个Yr(≠Y1)≤L处于警戒状态;K=2表示过程发出失控信号．根据Matlab程序编程给n1，n2，k，L，delta赋予最优值时能表现出比另外两个图较好的效果．下面举出数值例子．

当单元组的样本量为n2时，判断该单元组是否合格的区间为

3 数值例子

规定某种意义上的标准值，μ0=0，σ =1，δ1=0．2，τ=10 000．

对于休哈特控制图可以列出这样的等式这样可以利用Matlab给nX从1开始赋值，从而就可以得到相应的kX值，随之就确定了ATSX(δ1)的值，利用软件再找到最小的ATSX(δ1)值［6］．得

由

得

然后固定 n 值，得到一个区域．Dn={(n，k):k＞0，ATSg(0)≥τ，L=L*(n，k)}，最后用同样的方法使n从1开始取，从而得到最优的参数使得ATSg(δ1)最小，得

对于VGR控制图的数值例子，它和GR控制图不同之处就是当Yr≤L(Yr≠Y1)时，K=1，这时如果处于警戒状态，就增加单元组的样本量［7］．这里规定n2=1．25n1，可以通过计算机随机模拟得出．

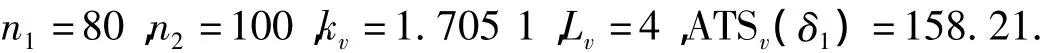
为了进一步比较VGR图、GR图以及休哈特控制图，给δ取定了不同的值．把GR图作为一个比较标准，即单位1，另外两个图得出的ATS(δ)值要与其做商，得表1以及图3．

表1 δ取不同值时GR控制图和休哈特控制图以及VGR控制图的比较Tab．1 Performance of the GR chart，Shewhart’s chart and VGR chart for various values of δ

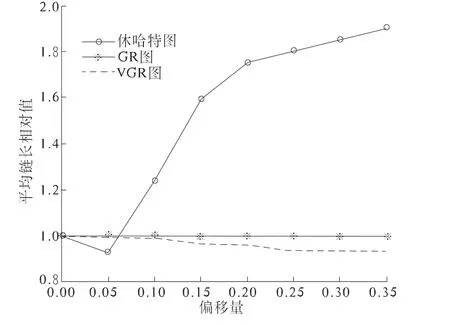
图3 休哈特图和GR图以及VGR图的ATS值的相对比较Fig．3 ATS comparation of Shewhart chart GR chart and VGR chart

4 结论

本文提出了可变样本的综合控制图，它是对传统休哈特控制图、合格品链长控制图以及可变样本3者的恰当结合．由于过程描述稍微复杂，采用流程图的方法把整个过程进行详细的描述．同时对休哈特控制图、GR控制图以及VGR控制图的设计与执行进行了概括．当均值未发生偏移时，3个要进行比较的控制图都有一个共同的标准，即ATS(0)≥τ．当均值发生较小偏移时，该文所研究的VGR控制图能表现出比另外两个图更好的效果．

［1］ Wu Z，Spedding T A．A synthetic control chart for detecting small shifts in the process mean［J］．Journal of Quality Technology，2000，32(1):32 －38．

［2］ Gadre M P，Rattihalli R N．A group runs control chart for detecting shifts in the process mean［J］．Economic Quality Control，2004，19(1):29－43．

［3］ Chang T C，Gan F F．Cumulative sum charts for high yield processes［J］．Statistica Sinica，2001，11(3):791 －805．

［4］ Davis R B，Woodall W H．Evaluating and improving the synthetic control chart［J］．Journal of Quality Technology，2002，34(2):63－69．

［5］ Ncube M M．An exponentially weighted moving average combined Shewhart cumulative score control procedure［J］．International Journal of Quality and Reliability Management，1990，7(6):29 －35．

［6］ 任景莉．一类非线性多边值问题正解的存在性［J］．郑州大学学报:理学版，2002，34(4):10－14．

［7］ 马宁，于洪志．基于Arnold变换和DCT变换的图像算法［J］．广西师范大学学报:自然科学版，2011，29(23):163－167．