Banach空间中可数簇全拟-φ-渐近非扩张非自映射的强收敛定理

李小蓉

(宜宾学院 数学学院, 四川 宜宾 644000)

1 预备知识

本文假设E是实Banach空间,E*是E的对偶,C是E的非空闭凸子集,J:E→2E*是按照如下方式定义的赋范对偶映射

J(x)={f*∈E*:〈x,f*〉=

‖x‖2=‖f*‖2,x∈E}.

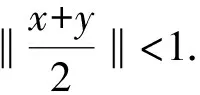
都有

设U={x∈E:‖x‖=1}是单位球面,称Banach空间E是光滑的,如果对∀x,y∈U,极限

存在.如果对∀x,y∈U,极限一致存在,则称E是一致光滑的.

设C是Banach空间E的一非空闭凸子集,称映射T:C→E是非扩张的,如果对∀x,y∈C都有

‖Tx-Ty‖≤‖x-y‖.

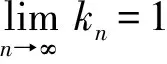
‖Tnx-Tny‖≤kn‖x-y‖, ∀x,y∈C.

本文用F(T)表示T的不动点集,即F(T)={x∈C:x=Tx}.设C是Banach空间E的子集,称映射C是E的收缩核,如果存在连续的映射P:E→C,使得Px=x,∀x∈C.显然一致凸Banach空间的每个非空闭凸子集都是E的收缩核.称映射P:E→C是非扩张的收缩映射,如果P是非扩张的,且是C到E的收缩的映射.

现在假设E是光滑的、严格凸、自反的Banach空间,C是E的非空闭凸子集.本文用φ:E×E→R+={a∈R|a>0}表示Lyapunov函数

φ(x,y)=‖x‖2-2〈x,Jy〉+‖y‖2, ∀x,y∈E.

由φ的定义可得

(‖x‖-‖y‖)2≤φ(x,y)≤

(‖x‖+‖y‖)2, ∀x,y∈E,

且

φ(x,J-1(λJy+(1-λ)Jz)≤

λφ(x,y)+(1-λ)φ(x,z), ∀x,y∈E.

∀x∈E.

引理1.1[2]设E是严格凸、光滑的Banach空间,则φ(x,y)=0当且仅当x=y.

引理1.2[2]E是自反、严格凸、光滑的Banach空间,D是E的非空闭凸子集,则有

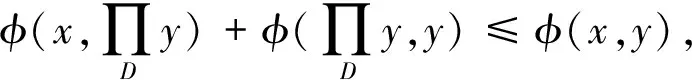
∀x∈D,y∈E.

引理1.3[2]E是自反、严格凸、光滑的Banach空间,D是E的非空闭凸子集,则有

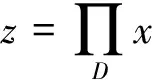
⟺〈z-y,J(x)-J(z)〉≥0, ∀y∈D.

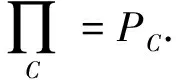
定义1.5设E是实Banach空间,C是E的非空闭凸子集,

1) 称C是E的收缩核,如果存在连续函数P:E→C,使得Px=x,∀x∈C;

2) 称P:E→C为保核收缩映射,如果P2=P;

3) 称P:E→C为非扩张的保核收缩映射,如果P是非扩张的,且为保核收缩映射.

定义1.6设P:C→E是非扩张的收缩映射,

1) 称自映射T:C→C为拟-φ-非扩张映射,如果F(T)≠Ø且

φ(u,Tnx)≤φ(u,x),

∀x∈C,u∈F(T),n≥1;

2) 称T:C→E为拟-φ-非扩张非自映射,如果F(T)≠Ø且

φ(u,T(PT)n-1x)≤φ(u,x),

∀x∈C,u∈F(T),n≥1;

3) 称T:C→E为拟-φ-渐近非扩张非自映射,如果F(T)≠Ø,且存在实序列{kn}⊂[1,∞),kn→1使得

φ(u,T(PT)n-1x)≤knφ(u,x),

∀x∈C,u∈F(T),n≥1.

注1.7由定义1.5可知,如果T:C→E是拟-φ-非扩张非自映射,则T为拟-φ-渐近非扩张非自映射(取kn=1).

引理1.8[3]设E是一致凸、光滑、自反的Banach空间,序列{xn}和{yn}⊂E.如果φ(xn,yn)→0,且{xn}或{yn}有界,则‖xn-yn‖→0.

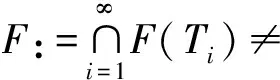
φ(u,Ti(PTi)n-1x)≤φ(u,x)+νnζ(φ(u,x))+μn,

∀n≥1,i≥1, ∀x∈C,u∈F.

多值的和单值的全拟-φ-渐近非扩张映像的例子见文献[4],该文中已指出,通常的广义渐近非扩张映像是全拟-φ-渐近非扩张映像的特例.

定义1.10称非自映射T:C→E为一致L-Lipschitz连续,如果存在常数L>0使得

‖T(PT)n-1x-T(PT)n-1y‖≤L‖x-y‖,

∀x,y∈C, ∀n≥1.

引理1.11设E是一致光滑、严格凸,且具有Kadec-Klee性质的Banach空间,C是E的非空闭凸子集.T:C→E是全拟-φ-渐近非扩张非自映射,ζ:R+={a∈R|a>0}→R+={a∈R|a>0}是严格增的连续函数,其中,ζ(0)=0,且当n→∞时,非负实序列νn→0,μn→0,如果μ1=0,则T的不动点集F(T)是闭集合.

证明令序列{un}⊆F(T),其中当n→∞时,un→u.由于T是全拟-φ-渐近非扩张非自映射,且μ1=0,故可得

故φ(u,Tu)=0,即u∈F(T).因此F(T)是闭集合.

关于渐近非扩张自映射或非自映射的强弱收敛、相对非扩张、拟-φ-非扩张、拟-φ-渐近非扩张自映射和非自映射的强弱收敛性,参见文献[5-29].

2 主要结论

定理2.1设E是一致光滑、严格凸、自反,且具有Kadec-Klee性质的Banach空间,C是E的非空闭凸子集.令{Ti:C→E,i=1,2,3,…}是一簇一致全拟-φ-渐近非扩张非自映射,对∀i≥1,Ti都是一致Li-Lipschitz连续映射.设实序列{αn}⊆[0,1],{βn}⊆(0,1)满足以下条件:

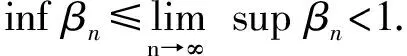
设xn是按以下方式生成的序列

∀x1∈E,C1=C;

yn,i=J-1[αnJx1+(1-αn)(βnJxn+

(1-βn)JTi(PTi)n-1xn],i≥1;

φ(z,x1)+(1-αn)φ(z,xn)+ξn};

其中

证明分5步证明此定理.

1) 首先证F和Cn是C的闭凸子集.

由引理1.11知F(Ti)是闭集合,又已知F是C的有界凸子集,故F是C的闭凸子集.

设序列{un}⊆F(T),且un→u.由于Ti:C→E是一簇全拟-φ-渐近非扩张非自映射,故

由已知C1=C是闭凸的.设当n≥2时Cn是闭凸集,下面证Cn+1是闭凸集.

φ(z,x1)+(1-αn)φ(z,xn)+ξn}=

(1-αn)φ(z,xn)+ξn}∩Cn=

2(1-αn)〈z,Jxn〉-2〈z,Jyn,i〉≤

αn‖x1‖2+(1-αn)‖xn‖2-‖yn,i‖2}∩Cn,

故Cn+1是闭凸集.

2) 证明对∀n≥1有F⊂C.

显然有F⊂C1=C.设对某个n≥2有F⊂Cn,令

wn,i=J-1(βnJxn+(1-βn)JTi(PTi)n-1xn),

对任何u∈F⊂Cn有

φ(u,yn,i)=φ(u,J-1(αnJx1+(1-αn)Jwn,i))≤

αnφ(u,x1)+(1-αn)φ(u,wn,i),

和

φ(u,wn,i)=φ(u,J-1(βnJxn+

(1-βn)JTi(PTi)n-1xn))≤

βnφ(u,xn)+(1-βn)φ(u,Ti(PTi)n-1xn)≤

βnφ(u,xn)+(1-βn)(φ(u,xn)+

νnζ(φ(u,xn))+μn)=

φ(u,xn)+(1-βn)(νnζ(φ(u,xn))+μn).

因此可得

{φ(u,xn)+(1-βn)(νnζ(φ(u,xn))+μn)}≤

αnφ(u,x1)+(1-αn){φ(u,xn)+

αnφ(u,x1)+(1-αn)φ(u,xn)+

αnφ(u,x1)+(1-αn)φ(u,xn)+ξn,

其中

即u∈Cn+1,因此F⊂Cn+1.

3) 证明序列{xn}⊂C强收敛于C中一点u*.

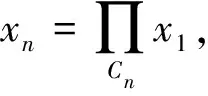
〈xn-y,Jx1-Jxn〉≥0, ∀y∈Cn.

又因为对∀n≥1,F⊂Cn,故可得

〈xn-u,Jx1-Jxn〉, ∀u∈F.

由引理1.2知,对∀n≥1,∀u∈F有

φ(u,x1)-φ(u,xn)≤φ(u,x1).

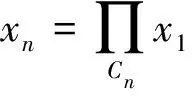
φ(xni,x1)≤φ(u*,x1), ∀ni≥1.

由于范数‖·‖是弱下半连续的,故可得

‖u*‖2-2〈u*,Jx1〉+‖x1‖2=φ(u*,x1),

故

则有

且‖xni‖→‖u*‖.因为xni⇀u*和E具有Kadec-Klee性质可得

由φ(xn,x1)收敛和

可得

φ(xn,x1)=φ(u*,x1).

现设存在序列{xnj}⊂{xn}也满足xnj→q,则由引理1.2可得

φ(u*,x1)-φ(u*,x1)=0,

故u*=q且

因此

4)证明u*∈F.

因为xn+1∈Cn+1和αn→0,故

(1-αn)φ(xn+1,xn)+ξn→0,n→∞.

由于xn→u*,且由引理1.7可得,对∀i≥1有

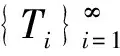
φ(u,Ti(PTi)n-1xn)≤φ(u,xn)+

νnζ(φ(u,xn))+μn,

故{Ti(PTi)n-1xn}是一致有界的.

‖wn,i‖=‖J-1(βnJxn+

(1-βn)JTi(PTi)n-1xn)‖≤

βn‖xn‖+(1-βn)‖Ti(PTi)n-1xn‖≤

‖xn‖+‖Ti(PTi)n-1xn‖,

即{wn,i}是一致有界序列.

由假设αn→0,对∀i≥1可得

因为J在E*的每个有界闭子集下是一致连续的,对∀i≥1可得

J在E的每个子集下是一致连续的可得

(1-βn)(JTi(PTi)n-1xn-Ju*)‖=

由条件(ii)可得

由于J是一致连续的,故

∀i≥1.

对∀i≥1,Ti是一致Li-Lipschitz连续可得

‖Ti(PTi)nxn-Ti(PTi)n-1xn‖≤

‖Ti(PTi)nxn-Ti(PTi)n-1xn+1‖+

‖Ti(PTi)nxn+1-xn+1‖+

‖xn+1-xn‖+‖xn-Ti(PTi)n-1xn‖≤

(Li+1)‖xn+1-xn‖+‖Ti(PTi)nxn+1-xn+1‖+

‖xn-Ti(PTi)n-1xn‖.

因为

且xn→u*,因此可得

且

即

由TiP的连续性,可得TiPu*=u*.因为u*∈C,Pu*=u*,故Tiu*=u*.由于i的任意性知u*∈F.

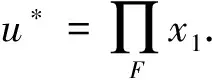
注2.2定理2.1与参考文献中的结果不同之处在于:本文在具有Kadec-Klee性质的一致光滑和严格凸Banach空间中研究了一类完全拟-φ-渐近非扩张非自映像簇的公共不动点的迭代逼近问题.而在参考文献中讨论的是:在一致凸和一致光滑的Banach空间中渐近非扩张非自映像(或广义渐近非扩张非自映像簇)的公共不动点的迭代逼近问题.本文的结果改进和推广了这些文献中的相应的结果.

致谢宜宾学院青年基金项目(2010Q29)对本文给予了资助,谨致谢意.

[1] Goebel K. Topics in Metric Fixed Piont Theory: Cambridge Studies in Advanced Mathematics[M]. Cambridge:Cambridge University Press,1990.

[2] Alber Y I. Metric and Generalized Projection Operators in Banach Spaces:Properties and Applications[C]//Theory and Applications of Nonlinear Operators of Accretive and Monotone Type. New York:Marcel Dekker,1996:15-50.

[3] Kiziltunc H, Temir S. Convergence theorems by a new iteration process for a finite family of nonself asymptotically nonexpansive mappings with errors in Banach spaces[J]. Comput Math Appl,2011,61(9):2480-2489.

[4] Chang S S. Strong convergence theorems of nonlinear operator equations for countable family of multivalued total quasi-φ-asymptotically nonexpansive mappings with applications[J]. Fixed Point Theory Appl,2012:69.

[5] Xu H K, Yin X M. Strong convergence theorems for nonexpansive nonself-mappings[J]. Nonlinear Anal,1995,24:223-228..

[6] Takahashi W, Kim G E. Strong convergence of approximants to fixed points of nonexpansive nonself-mappings in Banach spaces[J/OL]. Nonlinear Anal,1998(3),doi:10.1016/S0362-546X(97)00482-3.

[7] Chidume C E, Ofoedu E U, Zegeye H. Strong and weak convergence theorems for asymptotically nonexpansive mappings[J]. J Math Anal Appl,2003,280:364-374.

[8] Alber Y I, Reich S, Yao J C. Iterative methods for solving fixed-point problems with nonself-mappings in Banach spaces[J]. Abst Appl Anal,2003(2003):193-216.

[9] Matsushita S, Kuroiwa D. Approximation of fixed points of nonexpansive nonself-mappings[J]. Sci Math Jpn,2003,57:171-176.

[10] Song Y, Chen R. Viscosity approximation methods for nonexpansive nonself-mappings[J]. Math Anal Appl,2006,321:316-326.

[11] Chang S S, Joseph Lee H W, Chan C K. A new hybrid method for solving a generalized equilibrium problem solving a variational inequality problem and obtaining common fixed points in Banach spaces with applications[J]. Nonlinear Anal:TMA,2010,73:2260-2270.

[12] Su Y F, Xu H K, Zhang X. Strong convergence theorems for two countable families of weak relatively nonexpansive mappings and applications[J]. Nonlinear AnalTMA,2010,73:3890-3906.

[13] Chang S S, Chan C K, Joseph Lee H W. Modified Block iterative algorithm for quasi-φ-asymptotically nonexpansive mappings and equilibrium problem in Banach spaces[J]. Appl Math Comput,2011,217:7520-7530.

[14] YIldIrIm I, Ozdemir M. A new iterative process for common fixed points of finite families of non-self-asymptotically non-expansive mappings[J]. Nonlinear Anal:TMA,2009,71(3/4):991-999.

[15] Yang L P, Xie X S. Weak and strong convergence theorems of three step iteration process with errors for nonself-asymptotically nonexpansive mappings[J]. Math Comput Model,2010,52(5/6):772-780.

[16] Wang L. Strong and weak convergence theorems for common fixed points of nonself asymptotically nonexpansive mappings[J]. J Math Anal Appl,2006,323(1):550-557.

[17] Wang L. Explicit iteration method for common fixed points of a finite family of nonself asymptotically nonexpansive mappings[J]. Comput Math Appl,2007,53(7):1012-1019.

[18] Pathak H K, Cho Y J, Kang S M. Strong and weak convergence theorems for nonself-asymptotically perturbed nonexpansive mappings[J]. Nonlinear Anal:TMA,2009,70(5):1929-1938.

[19] Thianwan S. Common fixed points of new iterations for two asymptotically nonexpansive nonself-mappings in a Banach space[J]. J Comput Appl Math,2009,224(2):688-695.

[20] Qin X L, Cho S Y, Wang T Z, et al. Convergence of an implicit iterative process for asymptotically pseudocontractive nonselfmappings[J/OL]. Nonlinear Anal,2011,doi:10.1016/j.na.2011.04.031.

[21] Hao Y, Cho S Y, Qin X. Some weak convergence theorems for a family of asymptotically nonexpansive nonself mappings[J/OL]. Fixed Point Theory Appl,2010,doi:10.1155/2010/218573.

[22] Guo W P, Guo W. Weak convergence theorems for asymptotically nonexpansive nonself-mappings[J]. Appl Math Lett,2011,217(24):2181-2185.

[23] Nilsrakoo W, Sajung S. Strong convergece theorems by Halpern-Mann iterations for relatively nonexpansive mappings in Banach spaces[J]. Appl Math Comput,2011,217(14):6577-6586.

[24] Chang S S, Joseph Lee H W, Chan C K, et al. Approximation theorems for total quasi-φ-asymptotically nonexpansive mappings with applications[J]. Appl Math Comput,2011,218:2921-2931.

[25] Wang Z M, Su Y F, Wang D X, et al. A modified Halpern-type iteration algorithm for a family of hemi-relative nonexpansive mappings and systems of equilibrium problems in Banach spaces[J]. J Comput Appl Math,2011,235:2364-2371.

[26] Zegeye H, Ofoedu E U, Shahzad N. Convergence theorems for equilibrium problem, variational inequality problem and countably infinite relatively quasi-nonexpansive mappings[J]. Appl Math Comput,2010,216:3439-3449.

[27] Chang S S, Joseph Lee H W, Chan C K, et al. A modified Halpern-type iterative algorithm for totally quasi-φ-asymptotically nonexpansive mappings with applications[J]. Appl Math Comput,2012,218(11):6489-6497.

[28] Kamimura S, Takahashi W. Strong convergence of a proximal-type algorithm in a Banach space[J]. Appl Math Mech,2009,30:1105-1112.

[29] 雷贤才. 全渐近非扩张映象和无限族非扩张映象的强收敛定理[J]. 四川师范大学学报:自然科学版,2013,36(1):71-76.