具有同宿轨的系统在扰动下的分岔及混沌行为

朱长荣

(重庆大学 数学与统计学院, 重庆 401331)

由方程导出的动力系统，一直以来都是动力系统研究的重要内容.考虑下面的方程

(1)

其中,f∈Cr,r≥1.在满足初值x(0)=x0时，方程(1)的解是存在唯一的.如果存在x=x0，使得f(x0)=0，则称x0为方程(1)的平衡点，有时也称之为平衡解.如果方程(1)有平衡点x0，作适当平移以后，可以将x0移到原点，而系统的动力性态不改变.因此，以下总假设x0=0为系统的平衡点.记方程的解为x(t)=φt(x0).令U⊂RN为原点的适当开领域，下面定义原点的局部稳定流形和不稳定流形：

当t→∞,

且φt(x)∈U对所有t≥0},

且φt(x)∈U对所有t≤0}.

(2)

其中Df(0)是函数f在0点处的雅可比矩阵.如果Df(0)的所有特征值的实部不为零，则称0为双曲平衡点.由常微分方程的基本理论可知：方程(2)在双曲平衡点附近，会有维数分别为ns、nu的稳定和不稳定的不变子空间.方程(2)在双曲平衡点附近的稳定和不稳定的不变子空间与方程(1)在原点附近的局部稳定流形和不稳定流形之间，由下面的稳定流形定理说明了它们的关系[1-2].

正在研究的系统(1)，是实际问题经过高度抽象和舍弃许多细枝末节而得到的抽象系统.当补充上这些被舍弃的小节后，实际问题应该是下面的系统：

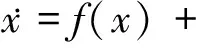
(3)

1 同宿轨的存在性

对这个问题的研究，一直以来有2个主要的方法：几何的方法和分析的方法.这2个方法现在任然是研究同宿轨的保持性和破裂的重要方法.令x∈R2，g关于t是周期的，g(0,t,)=0(这个条件不是本质的，因为只要做个平移，总可以办到).1963年，V. K. Melnikov[5]从几何的观点入手，应用Poincaré映射的方法，来研究系统(3)在很小的参数时的同宿轨的存在性.因为0对方程(1)是双曲的，它有一维的稳定流形和不稳定流形.则对于方程(3)，它的平衡点附近也有在γ附近的一维的稳定流形和不稳定流形.在γ(0)处取一小段横截痕Σt0，则(3)的稳定流形和不稳定流形与Σt0分别相交于和定义距离

d

很显然d0(t0)=0，并且如果存在t0，使得d(t0)=0，则扰动方程在γ附近就存在同宿轨γ.定义Melnikov函数

其中∧是外积.如果将d(t0)沿着展开，M(t0)与展开式的一次项紧密相关.可以证明，如果存在t0，使得M(t0)=0，DM(t0)≠0,则方程(3)在γ附近就存在同宿轨γ.这个方法就是著名的Melnikov方法.

在接下来的近20年中，人们在研究同宿轨的保持性时，大都采用几何的方法.直到1980年，在文献[10]中，S. N. Chow等从几分析的观点出发，考虑如下系统的同宿轨问题

(4)

其中f(t+T)=f(t).很显然，当λ=(λ1,λ2)=(0,0)时，系统(4)有一对同宿轨，并且(0,0)也是当λ=(0,0)时，系统(4)的双曲平衡点.他们在参数原点附近找到一个领域U以及通过原点的曲线Cm、CM，Cm、CM将U分成4个部分.当参数在其中的2个部分时，系统(4)会出现同宿轨；当参数在另外的两个部分时，系统(4)就不会出现同宿轨.

现在对(3)式作一些假设:

(A1)f和g都是C3的；

(A2)f(0)=0并且矩阵Df(0)的特征值的实部不等于零；

(A3) 系统(1)有一条同宿于原点的同宿轨；

(A4)g(0,t,)=0；

(A5)g(x,t,)=g(x,t+T,).

到1984年，K. J. Palmer[7]应用分析的方法，在方程(1)有一条非退化的同宿轨的假设下，将文献[10]中的结果推进到RN.在文献[7]中，K. J. Palmer不仅得到了这条非退化同宿轨得到保持的条件，还给出了关于(3)的“Shadowing Lemma”.具体情况如下：

令n为正整数，为ψn双边无穷序列所构成的集合：a=(…,a-1,a0,a1,…),其中ak∈{0,1,…,n-1}.在乘积拓扑下，ψn是一个完全不连通的紧Housdorff空间(Cantor集).定义同胚映射β为(β(a))k=ak+1，β常称为Bernoulli平移.在文献[7]中有下面的结论：

定理2[7]在假设(A1)～(A5)下，如果方程(3)有一个T-周期解u和另一个解v满足:

(I) (3)式沿着v的线性变分方程在(-∞,∞)上有指数二分性；

(II) |v(t)-u(t)|→0当|t|→∞.

|xa(t+(2k-1)mT)-v(t+akT)|≤,

其中k为整数，-mT≤t≤mT.映射φ(a)=xa(0)是RN中的一个紧子集上的同胚，在这个紧子集上，(3)式的解的周期映射F的2m-次迭代F2m是不变的且满足：F2m∘φ=φ∘β.

定理2常常用来证明具有周期映射的系统，如果存在横截的同宿轨，则在横截的同宿轨附近会出现马蹄形混沌.因为定理2是说，对于解v，它有n段相应于时间[-mT,mt],[-(m-1)T,(m+1)T],…,[-(m-n+1)T,(m+n-T)]的弧，周期系统有一条在这些弧之间可以任意转换的轨道xa，它在每一时间段[(2k-2)mT,2kmT]上“shadow”了这些弧.

在这之前，人们大都在做关于非退化同宿轨方面的工作，J. K. Hale在文献[11]中建议考虑带多参数的具有退化同宿轨的分岔问题.20世纪90年代，许多人[12-19]开始研究具有两个参数的带退化同宿轨的问题:g(x,t,)=1g1(x,t,)+2g2(x,t,).在文献[15]中，J. Gruendler考虑了g不依赖于时间t的自治扰动，在文献[16]中，他将扰动推进到一般的非自治扰动.更进一步，如果扰动g是周期的，J. Gruendler在文献[17]中证明，被保持下来的同宿轨是横截的，因此周期扰动系统就具有混沌特性.在考虑退化的同宿轨时，扰动函数不仅依赖于沿着同宿轨的切方向，还有沿着同宿轨的法方向；而如果同宿轨是非退化的，则只有切方向.为了解决法方向带来的困难，J. Gruendler先对线性变分方程的解进行分类，分类如下：

引理1[16]在假设(A1)～(A3)下，方程(2)存在矩阵解U，正常数K,α以及4个投影算子Pss、Psu、Pus、Puu满足Pss+Psu+Pus+Puu=I并且,

(a) 当0≤s≤t时,|U(t)(Pss+Psu)U(s)-1|≤Ke2α(s-t),

(b) 当0≤t≤s时,|U(t)(Pus+Puu)U(s)-1|≤Ke2α(t-s),

(c) 当t≤s≤0时,|U(t)(Pss+Pus)U(s)-1|≤Ke2α(t-s),

(d) 当s≤t≤0时,|U(t)(Psu+Puu)U(s)-1|≤Ke2α(s-t).

并且Rank(Pss)=Rank(Puu):=d.

令ui(t)是U(t)的第i-列.则相应于投影算子Pss、Psu、Pus、Puu，这4类解为：

∀ui∈PusU,

∀ui∈PsuU,

∀ui∈PuuU,

∀ui∈PssU.

不失一般性，可以假设：

令U-1为U的逆，则有：

PuuU=[u1,…,ud],

PssU=[ud+1,…,u2d].

引入记号，令

Φi(λ,,θ)

其中

J. Gruendler在文献[16]中得到下面的结论：

定理3[16]在假设(A1)～(A4)下，如果存在θ使得(Φi(λ(θ),(θ),θ))=0(λ(θ),(θ))θ，并且矩阵C(θ)=(cij(θ))(d-1)×(d-1)满秩：

cij(θ)=ηij+1-d(θ),j=d,d+1,

则存在开集0∈I⊂R以及可微函数ψ:I→R2,使得方程(3)在=s2((θ)+ψ(s))时有同宿轨,s∈I.

在1996年，J. Gruendler在文献[17]中推广文献[13]关于混沌的结果证明了：如果扰动函数是周期的，则扰动方程的解决定的周期映射在同宿轨附近会出现马蹄形混沌B,该结果后来被推广到高维空间中[21-23].

2 多条同宿轨的并存性

上面的结论能够回答这样的问题：在没有扰动的系统存在同宿轨的情况下，在适当的横截性条件下，扰动系统会出现同宿轨.但不能回答这样的问题：在没有扰动的系统的同宿轨是退化的情况下，扰动系统能有多少条同宿轨.这个问题直到最近才有了答案：沿用引理1的符号，C. Zhu等在文献[24]中证明了，对任意的，扰动系统可以存在条不同的同宿轨.在(3)式中，研究者们把∈R作为参数，这是一个一维的扰动问题.如果增加扰动函数的自由度，将整个函数空间C3(RN×R,RN)作为扰动参数，则问题就变为下面的问题：

(5)

其中‖g‖C3很小.在C3(RN×R,RN)中定义子空间：

={g∈C3(RN×R,RN)|g(0,t)=0,

C. Zhu等在文献[24]中得到了下面的结论：

定理4[24]如果假设(A1)～(A3)成立，并且ζijj≠0.则在中存在领域和d个余维为kd的经过原点的子流形Γk,k=1,…,d，使得当g∈∩(Γk(Γk+1∪…∪Γd))时，方程(5)有k个不同的同宿轨.

以上介绍的是正常扰动条件下的同宿轨分岔问题.还有一类扰动—奇异扰动问题：

g(x,t,),

(6)

方程(6)与方程(3)有很大的区别：前者对参数是不连续；当把方程(6)转化为等价的积分方程时，积分方程的解的增长性不能较好地控制.基于这些困难C. Zhu等在文献[25]中考虑了如下的方程的同宿轨的分岔问题：

(x,t,).

(7)

方程中的g任然看做在C3(RN×R×R,RN)中的扰动函数.在引进截断函数等新的工具后，作者在文献[25]中得到与定理4相似的结果.

文献[24-25]的工作表明：当没有扰动的方程的同宿轨是退化的情况下，作适当的扰动，扰动系统可能会出现从1到d条不同的同宿轨.当扰动系统出现一条同宿轨时(即扰动系统存在同宿轨)，文献[24-25]中的结果表明：扰动参数需要d维，即扰动余维为d.与前面的定理2、3相比较，他们的工作表明，如果只考虑扰动系统的同宿轨的存在性，扰动维数只需要1维就够了.从这个角度讲，文献[24-25]中的扰动维数太大，可能扰动系统出现k条同宿轨，并不需要kd维的扰动余维数.这个问题正在考虑中.

3 白噪声下的同宿轨的保持性

以上讨论同宿轨的分岔时，都是确定性系统.最近，很多学者[26-31]讨论了由Brownian运动引起的随机过程扰动下，同宿轨的保持性以及由此产生的混沌运动.就一般而言，Brownian运动是一个无界运动，因此这个问题就不是刚才的小扰动问题.

令(Ω,,)表示经典的Wiener概率空间，在紧开拓扑下，

Ω={ω(t)|ω(·):R→Rω(0)=0}

dx(t)=f(x(t))dt+g(x(t))∘dB(t),

(8)

θtω(·)=ω(t+·)-ω(t).

对任意给定的Δ>0,令:Ω→R定义为：

对每个ω∈Ω,得到由此可以看出，(ω)可以被看做白噪声在t=0时刻的离散情形.在定义了,得到

(9)

这是一个带有正态分布的平稳随机过程.由Brownian的特性,(θtω)几乎处处无界，且(θtω)可看做白噪声的离散形式.在文献[31]中,K. Lu等用几何的方法，考虑了如下系统的同宿轨的保持性与混沌：

其中μ是小参数,f,g,P,Q在原点附近是Cr的，r>2.假设f(0,0)=g(0,0)=P(0,0)=Q(0,0)=0，且μ=0时，方程(10)有一条同宿轨γ(t)=(a(t),b(t))，通过在同宿轨附近引入回复映射，他们得到下面的结论：

定理5[31]如果存在t∈R使得

b′(t)P(a(t),b(t))-a′(t)Q(a(t),b(t))≠0,

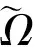
对于有同宿轨或异宿轨的系统，在白噪声下的在同宿轨或异宿轨附近的动力行为还有很多没有解决.在同宿轨非要进还有另外一种十分重要的现象，次调和分叉，就是当同宿轨在小扰动下不能保持而破裂，在破裂的同宿轨附近出现周期解的现象[8-9,32-36]等.对于在同宿轨或异宿轨附近发生的分叉或它们的保持性，还有很多学者得到了很好的结果，比如文献[37-52]等等.

[1] Hale J K. Ordinary Differential Equations[M]. New York:Wiley-Interscience,1969.

[2] Chow S N, Hale J K. Methods of Bifurcation Theory[M]. New York:Springer-Verlag,1982.

[3] Palmer K J. Transversal heteroclinic orbits and Cherry’s example of a non-integrable hemiltonian system[J]. J Diff Eqns,1986,65:321-360.

[4] Zeng W. Exponential dichotomies and transversal homoclinic orbits in degenerate cases[J]. J Dyn Diff Eqns,1995,7:521-548.

[5] Melnikov V K. On the stability of the center for time periodic perturbations[J]. Trans Moscow Math Soc,1963,12:1-57.

[6] Neimark J I, Silnikov L P. A case of generation of periodic motions[J]. Soviet Math Docl,1965,6:1261-1264.

[7] Palmer K J. Exponential dichotomies and transversal homoclinic points[J]. J Diff Eqns,1984,55:225-256.

[8] Silnikov L P. A case of the existence of a countable number of periodic motions[J]. Soviet Math Dokl,1965,6:163-166.

[9] Silnikov L P. On a Poincaré-Birkhoff problem[J]. Math USSR-Sb,1967,3:353-371.

[10] Chow S N, Hale J K, Mallet-Paret J. An example of bifurcation to homoclinic orbits[J]. J Diff Eqns,1980,37:551-573.

[11] Hale J K. Bifurcation theory and applications[C]//Lecture Notes in Mathematics. Berlin:Springer-Verlag,1984,1057:106-151.

[12] Battelli F, Lazzari C. Exponential dichotomies, heteroclinic orbits, and Melnikov functions[J]. J Diff Eqns,1990,86:342-366.

[13] Battelli F, Palmer K J. Tangencies between stable and unstable manifolds[J]. Proc Roy Soc Edin,1992,A121:73-90.

[15] Gruendler J. Homoclionic solutions for autonomous systems in arbitrary dimension[J]. SIAM J Math Anal,1992,23:702-721.

[16] Gruendler J. Homoclinic solutions for autonomous ordinary differential equations with nonautonomous perturbations[J]. J Diff Eqns,1995,122:1-26.

[17] Gruendler J. The existence of transversal homoclinic solutions for higher order equations[J]. J Diff Eqns,1996,130:307-320.

[18] Hale J K, Lin X B. Heteroclinic orbits for retarded functional differential equations[J]. J Diff Eqns,1986,65:175-202.

[19] Knobloch J. Bifurcation of degenerate homoclinic orbits in reversible and conservative systems[J]. J Dyn Diff Eqns,1997,9:427-444.

[20] Battelli F, Palmer K J. Chaos in the Duffing equation[J]. J Diff Eqns,1993,101:276-301.

[21] Luo G, Zhu C. Transversal homoclinic orbits and chaos for functional differential equations[J]. Nonlinear Anal:TMA,2009,71:6254-6264.

[22] Zhu C, Luo G, Shu Y. The existences of transverse homoclinic solutions and chaos for parabolic equations[J]. J Math Anal Appl,2007,335:626-641.

[23] Awrejcewicz J, Holicke M M. Smooth and Nonsmooth High Dimensional Chaos and the Melnikov-Type Methods[M]. Singapore:World Scientific,2007.

[24] Zhu C, Zhang W. Linearly independent homoclinic bifurcations parameterized by a small function[J]. J Diff Eqns,2007,240:38-57.

[25] Zhu C, Luo G, Lan K. Multiple homoclinic solutions for singular differential equations[J]. Ann Inst H Poincare:AN,2010,27:917-936.

[26] Arnold L. Random Dynamical Systems[M]. New York:Springer-Verlag,1998.

[27] Jaeger L, Kantz H. Homoclinic tangencies and non-normal Jacobians-effects of noise in nonhyperbolic chaotic systems[J]. Physica,1997,D105:79-96.

[28] Kennedy J, York J. Topological horseshoes[J]. Trans Am Math Soc,2001,353:3513-2530.

[29] Lu K, Wang Q. Chaos in differential equations driven by a nonautonomous force[J]. Nonlinearity,2010,23:2935-2975.

[30] Lu K, Wang Q. Chaos behavior in differential equations driven by a Brownian motion[J]. J Diff Eqns,2011,251:2853-2895.

[31] Chow S N, Deng B, Terman D. The bifurcation of homoclinic and periodic orbits from two heteroclinic orbits[J]. SIAM J Math Anal,1990,21:179-204.

[32] Guckenheimer J, Holmes P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields[M]. New York:Springer-Verlag,1983.

[33] Hale J K, Spezamiglio A. Perturbation of homoclinics and subharmonics in Duffing’s equation[J]. Nonlinear Anal:TMA,1985,9:181-192.

[34] He Z, Zhang W. Subharmonic bifurcations in a perturbed nonlinear oscillation[J]. Nonlinear Anal:TMA,2005,61:1057-1091.

[35] Zhu C. The coexistence of subharmonics bifurcated from homoclinic orbits in singular systems[J]. Nonlinearity,2008,21:285-303.

[36] Bulsara A R, Schieve W C, Jacobs E W. Homoclinic chaos in systems perturbed by weak Langevin noise[J]. Phys Rev,1990,A41:668-681.

[37] Deng G, Zhu D. Homoclinic and heteroclinic orbits for near-integrable coupled nonlinear Schrödinger equations[J]. Nonlinear Analysis:TMA,2010,73:817-827.

[38] Freddy D, Li C, Zhang Z. Unfolding of a quadratic integrable system with two centers and two unbounded heteroclinic loops[J]. J Diff Eqns,1997,139:146-193.

[39] Gan S, Wen L. Heteroclinic cycles and homoclinic closures for generic diffeomorphisms[J]. J Dyn Diff Eqns,2003,15:451-471.

[40] Han M, Hu S, Liu X. On the stability of double homoclinic and heteroclinic cycles[J]. Nonlinear Anal:TMA,2003,53:701-713.

[41] Li W, Lu K. Sternberg theorems for random dynamical systems[J]. Commun Pure Appl Math,2005,58:941-988.

[42] Lin X. Using Melnikov’s method to solve Silnikov’s problem[J]. Proc Roy Soc Edin,1990,A116:295-325.

[43] Lin X, Vivancos I B. Heteroclinic and periodic cycles in a perturbed convection model[J]. J Diff Eqns,2002,182:219-265.

[44] Liu B, Zanolin F. Boundedness of solutions of nonlinear differential equations[J]. J Diff Eqns,1998,144:66-98.

[45] Luo G, Liang J, Zhu C. The transversal homoclinic solutions and chaos for stochastic ordinary differential equations[J/OL]. J Math Anal Appl,2013,doi:10.1016/j.jmaa.2013.10.055.

[46] Palmer K J. Exponential dichotomies for almost periodic equation[J]. Proc Am Math Soc,1987,101:283-298.

[47] Palmer K J, Stoffer D. Chaos in almost periodic systems[J]. Z Angew Math Phys,1989,40:592-602.

[48] Palmer K J. Existence of transversal homoclinic points in a degenerate case[J]. Rocky Mount J Math,1990,20:1099-1118.

[49] Wiggins S. Global bifurcations and chaos-analytical methods[J]. New York:Springer-Verlag,1988.

[50] Zhang W. Bifurcation of homoclinics in a nonlinear oscillation[J]. Acta Math Sinica:Engl,1989,5:170-184.

[51] Deng B. The bifurcations of countable connections from a twisted heteroclinic loop[J]. SIAM J Math Anal,1991,22:653-679.

[52] Holmes P, Marsden J. Horseshoes in perturbations of Hamiltonian systems with two degrees of freedom[J]. Commun Math Phys,1981,82:523-544.