具有Markov转换的Lotka-Volterra系统中市场结构的演进

付桐林

(陇东学院 数学与统计学院, 甘肃 庆阳 745000)

Lotka-Volterra模型由Lotka和Volterra提出,最初用于描述生态学中种群的动态关系.近年来在经济研究中开始有所应用，但大部分结果都仅仅局限于经济增长和社会人口控制等宏观问题.J. Brandera等[1]在一个简单的一般均衡体系下采用Lotka-Volterra模型讨论了社会文明的动态过程,付桐林等[2-3]研究了随机Lotka-Volterra竞争系统下的市场结构,证明了市场结构的依分布稳定性和随机持久性.S. Slobodyan[4]利用Lotka-Volterra模型证明了在局部不确定的稳态下,连续时间的经济增长模型不可能存在周期性轨道.C. Zhu等[5-6]先后研究了随机环境下的Lotka-Volterra模型,给出了系统解的存在唯一性定理.X. Li等[7]研究了随机干扰下的Lotka-Volterra人口模型.

市场产品结构的确立,传统上是在市场处于均衡态的假设下以边际成本与边际收益相等作为厂商决策的依据,并以此来确定市场结构.孔东民[8]避开市场处于均衡态的假设和边际成本等于边际收益的条件,研究了Lotka-Volterra系统下市场结构的演进.这些研究都是借用确定性Lotka-Volterra系统对经济领域的问题加以讨论.事实上,当多种同类的竞争性产品投放市场后,会受到各种微小的随机因素的干扰.而生产产品有时也会受到干扰强度很大的随机因素如停电、维修、事故等的影响转入停产状态,而这些随机因素的来到时刻也具有很强的随机性.文中用Markov链来描述这种突然地强度很大的随机干扰[9-11],采用具有Markov转换的Lotka-Volterra系统描述市场结构,这样更加贴近现实.

1 主要结果

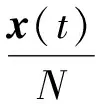
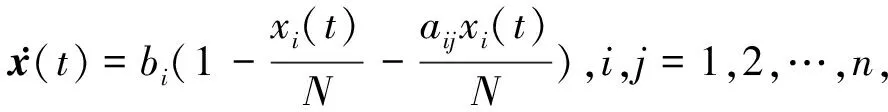
事实上,上述n种同类的竞争性产品投放市场后,会受到各种微小的随机因素的干扰.而生产产品有时也会受到干扰强度很大的随机因素如停电、维修、事故等的影响转入停产状态,而这些随机因素的来到时刻也具有很强的随机性.文中用Markov链来描述这种突然地强度很大的随机干扰.考虑带有Markov转换和白噪声干扰的如下形式的Lotka-Volterra方程

[b(α(t))+A(α(t))x(t)]dt+

σ(α(t))x(t)dB(t),

(1)

其中,B(t)是标准Brown运动[12],α(t)是取值在S=1,2,…,M的右连续Markov链,满足对每个α∈S有σii>0,σij≥0，i≠j,i,j=1,2,…,M.

这里

σ(α(t))=(σij(α(t)))n×n.

≤K,

其中K是常数.

dV(x(t))=LV(x(t))dt+

xT(t)σ(α(t))x(t)dB(t),

其中

LV(x(t))=xT(t)b(α(t))+xT(t)A(α(t))x(t).

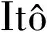
d(etV(x(t)))=etV(x(t))dt+

etdV(x(t))=et[V(x(t))+LV(x(t))]dt+

etxT(t)σ(α(t))x(t)dB(t).

对每个整数k≥|x0|,停时ρk=inf{t∈R+:|xt|≥k}.于是

+V(x(s))]ds=et[V(x(t))+

LV(x(t))]dt+etxT(t)σ(α(t))x(t)dB(t), (2)

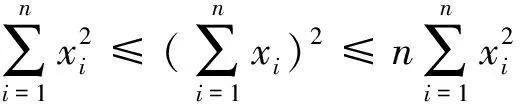
LV(x(t))+V(x(t))=xT(t)b(α(t))+

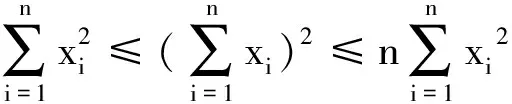
基于引理和Chebyshev不等式[13],有如下定理.

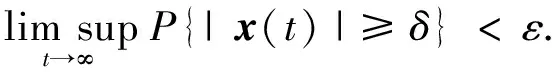
定理1说明方程(1)的解为随机最终有界的,这说明在各种随机因素的干扰之下,构成系统的各种产品的数目终将随机的维持在各自的均衡点附近.下面的定理给出了方程(1)的渐近行为.

即

|xT(s)A(α(s))x(s)|≤

因此

令

则

因而

对1≤t≤k,∀ω∈Ω′,∀k≥k0(w)成立.若k-1≤t≤k且k≥k0(w),则有

于是

即

致谢陇东学院青年科技创新项目(XYZK1208)对本文给予了资助，谨致谢意.

[1] Brandera J, Taylorm S. The simple economics of Easter Island:a ricard malthus model of renewable resource use[J]. Am Economic Rev,1998,88(1):119-138.

[2] 付桐林. 随机Lotka-Volterra竞争系统下的市场结构的演进[J]. 曲阜师范大学学报:自然科学版,2013,39(2):47-50.

[3] 付桐林,杨明霞. Markov转换的随机Lotka-Volterra竞争系统下的市场结构的演进[J]. 黄冈师范学院学报,2012,32(6):5-7.

[4] Slobodyan S. On impossibility of limit cycles in certain two dimensional continuous time grouth model[J]. Studies in Nonlinear Dynamics and Econometrics,2001,5(1):33-40.

[5] Zhu C, Yin G. On hybrid competitive Lotka-Volterra ecosystems[J]. Nonlinear Anal,2009,71:1370-1379.

[6] Zhu C, Yin G. On competitive Lotka-Volterra model in random environments[J]. J Math Ana Appl,2009,357:154-170.

[7] Li X, Mao X. Population dynamical behavior of non autonomous Lotka-Volterra competitive systems with random perturbation[J]. Discrete and Continuous Dynamical Systems,2009,24:523-545.

[8] 孔东民. Lotka Volterra系统下市场结构的演进[J]. 管理工程学报,2005,19(3):77-81.

[9] 吕王勇,高仕龙,马洪. 广义Copula的存在理论[J]. 四川师范大学学报:自然科学版,2010,33(2):159-161.

[10] 付桐林,潘欢. 尾分布族L、D的一些性质及其应用[J]. 兰州理工大学学报:自然科学版,2010,36(3):162-165.

[11] Embrocates P, Kluppelberg C, Mikosch T. Modelling Extreme Events for Insurance and Finance[M]. Berlin:Springer-verlag,1997.

[12] Rolski T, Schmidt H, Schmidt Y,et al. Stochastic Process for Insurance and Finance[M]. Johe Wiley & Sons,1999.

[13] Stevene Shreve. Stochastic Calculus for Finance[M]. New York:Springer-verlag,2008:251-269.

[14] 闫秀明,胡先权. 新环状势的Klein-Gordon方程束缚态解[J]. 重庆师范大学学报:自然科学版,2010,27(4):51-53.

[15] 马月珍,李小纲,葛永斌. 二维波动方程的高精度交替方向隐式方法. 四川师范大学学报:自然科学版,2010,33(2):179-183.

[16] 邵远夫,艾武. 一类脉冲多时滞互惠系统周期解的存在性与稳定性[J]. 四川师范大学学报:自然科学版,2012,35(1):33-38.