结构模糊非概率混合可靠性分析方法
许孟辉 邱志平
(北京航空航天大学 固体力学研究所,北京 100191)
工程领域总是存在各种不确定性,其数据类型和可用信息容量决定其数学描述形式.工程结构不确定性源于因果关系不充分或界限不明确,前者引起的结果不可预知性本质为因果律的缺失而导致的随机性,可由概率统计规律描述,后者引起的边界不清晰性本质上为排中律的缺陷导致的模糊性,可由模糊可能性理论描述.在新工艺新材料广泛应用的结构中,结构参数有限的试验数据造成概率统计理论及可能性理论实际应用的困难,即在小样本条件下拟合结构参数的概率密度函数或隶属度函数具有较大误差,且在后续分析与设计中因结构非线性等因素造成误差超出可接受范围.参数区间模型仅需确定参数分布范围的上下界而无需参数分布类型,在结构分析设计领域中得到广泛的应用.
结构参数的不确定性会引起结构功能波动而无法发挥其规定效用甚至造成结构失效.结构可靠性是研究结构在各种因素作用下的安全问题,描述结构在规定条件下和规定时间内完成规定功能的能力.传统可靠性分析采用概率模型来描述结构不确定性,设计要求为结构失效概率小于允许失效概率[1].但概率模型需要足够数据确定概率密度函数,这些数据往往不易准确获知,若对概率密度函数作人为假设,则分析结果可能存在较大误差[2].对于统计数据不足而难以确定概率密度函数的情况,文献[2]主张采用凸集模型描述不确定性,将不确定性视为有界量,通过反优化予以考虑.与此同时,结构分析设计过程存在许多模糊不确定性,如机械零件的失效磨损尺寸、结构允许的最大变形位移等[3].模糊理论是处理模糊不确定性的重要工具.传统模糊可靠性分析是基于模糊随机干涉可靠性理论[4-5].文献[6 -7]修改了概率可靠性两个基本假设,提出了模糊状态和可能性假设可靠性理论.文献[8]基于可能性理论,提出了结构的能度可靠性方法.然而,实际工程结构可能存在多种不确定性共存的情形,如在机翼结构初始设计阶段,某些结构参数由于试验数据不足而大多采用区间变量或模糊变量,而随试验数据的增加将某些结构参数定量化为随机变量.如何对多种不确定性共存的结构进行可靠性分析[9-11]成为一个具有实际意义的问题.对概率非概率不确定性[9-12]、概率模糊不确定性[3]及模糊非概率不确定性共存[13-14]下的可靠性分析已有部分研究.文献[13-14]方法基于“逐层分析”思想,将非概率区间变量或模糊变量取其某一实现,进一步按照能度可靠性或非概率可靠性理论分析结构可靠性.根据模糊性与非概率不确定性的“可缩减”性质,即模糊性与非概率不确定性随相关数据信息的增加而减少,可将这两种形式不确定性统一考虑.
针对含模糊非概率混合变量的可靠性问题,现有研究主要从模糊失效准则出发刻画结构可靠度分析过程中的模糊性.本文基于模糊数学分解原理,将模糊非概率混合可靠性问题转化为一系列不同隶属度下非概率可靠性分析问题,通过在[0,1]内遍历隶属度值实现结构可靠度的模糊性定量化.在非概率可靠性分析中,可靠度的求解存在计算量与精度间的显著矛盾.本文基于逐维策略和Chebyshev模型将结构功能函数最值的计算转化为最值点向量的逐维确定过程,通过功能函数在最值点向量处的精确值确定功能函数的界限以计算结构可靠度.
1 模糊非概率混合可靠性问题
含有模糊变量和区间变量的结构功能函数可表示为

根据模糊数学分解原理,模糊变量等价于在[0,1]内连续分布的隶属度水平下的闭区间变量.本文将区间向量yI视为具有特殊隶属度函数的模糊向量,即对于任意的 j∈{1,2,…,n},区间变量的隶属度函数可以表示为μj(yj)≡1,且在任意隶属度λ∈[0,1]下的截集仍为其本身,即
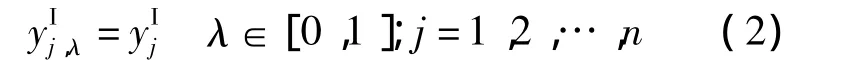
因此,模糊非概率混合变量分析问题转化为一系列隶属度下的非概率分析问题,且通过下面的命题可以证明:由自变量在隶属度λ下诱导的定义域所决定的函数值域为相同隶属度下因变量的截集.
命题 若结构功能函数M是具有连续隶属度函数的结构参数 x~,yI的连续函数,且由定义域确定的函数M的值域为紧集,则在可能度λ下结构功能函数M的截集Mλ可以表示为

即
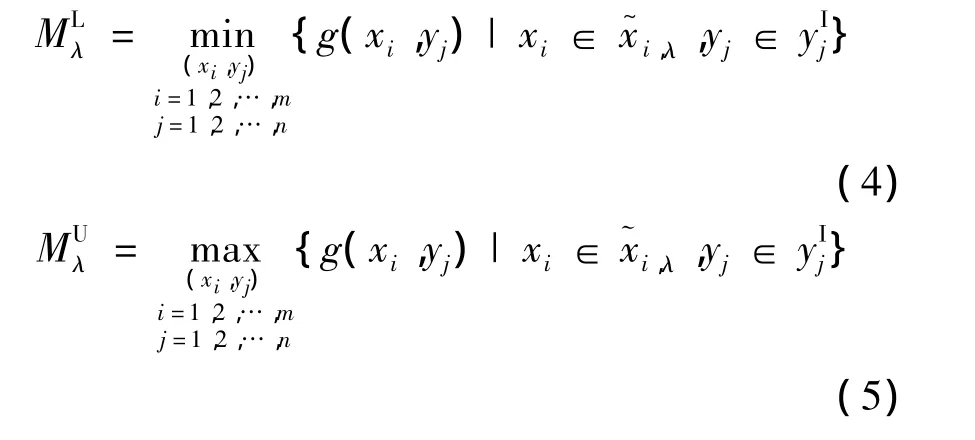
证明 对于任意给定的m1,满足条件:

则存在向量x1和y1,满足:

且有
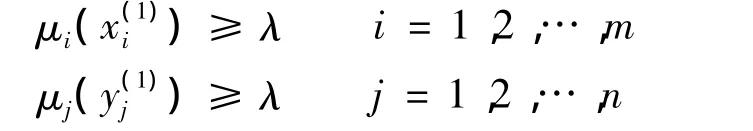
由 Zadeh 扩张原理[15]可得
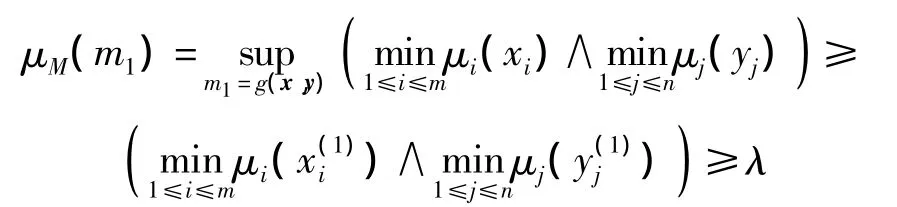
式中符号∧表示取小运算,则有m1∈Mλ,从而
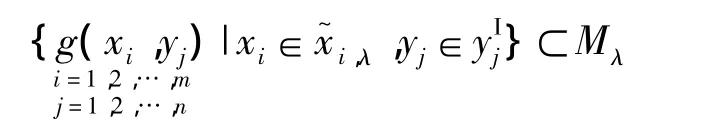
相反地,对于任意的m2∈Mλ,有


满足:

且


从而

综上所述有

证毕
一般而言,工程领域结构功能函数为结构参数的连续函数,并且其值域为紧集.给定隶属度λ,模糊向量转化为区间向量,区间向量yI亦为该隶属度下的区间向量,即相应地,结构功能函数转化为在给定隶属度下仅含区间向量和 yI的函数,即
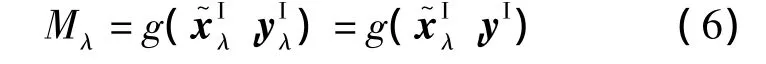
根据非概率区间可靠性分析的最短距离模型[16],设在可能度λ下结构功能函数Mλ的中心值和半径分别表示为和,则结构可靠度可表示为


即结构在隶属度λ下是安全可靠的.若ηλ<-1,则
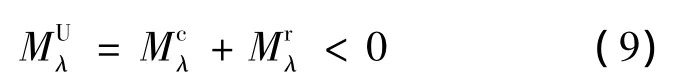
即结构在隶属度λ下必然失效.
2 模糊非概率混合可靠性分析算法
在结构分析设计领域,结构功能函数往往表现为非线性高维隐式函数.由式(7)可知,结构可靠度由功能函数的界限值决定,顶点法和优化法等常用于功能函数界限值的计算,但顶点法对非线性函数界限值估计误差较大,优化法对隐式高维函数界值的计算存在精度和效率间的矛盾.本文基于函数Chebyshev近似模型及配点方法提出功能函数最值点逐维确定策略以高效精确地计算功能函数在给定可能度下的界限值.
为说明的方便,在给定可能度λ下,记
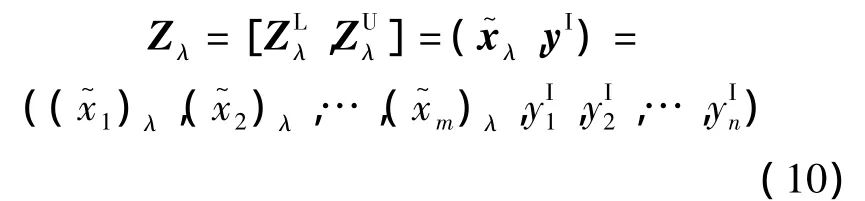
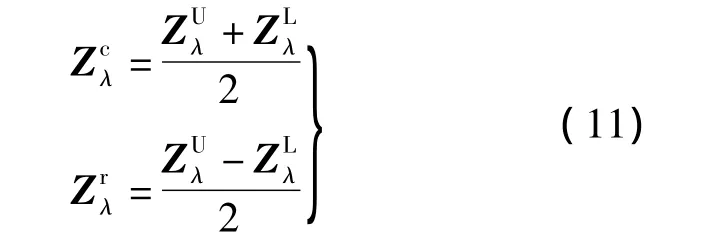
因此向量Zλ可分解为均值和半径的线性组合形式,即

式中,zλ表示绝对值不大于1的变量组成的m+n维向量;符号×表示向量对应元素作乘积运算.因此,结构功能函数可以表示为

选择 zλ,i,i∈{1,2,…,m+n}为逼近参数且zλ,j(j=1,2,…,m+n;j≠i)取均值,并记退化的功能函数为

为本文理论推导的需要,式(14)简记为

本文提出的逐维策略是基于Chebyshev多项式模型和配点方法.为此,首先引入第1类Chebyshev 多项式[17]:
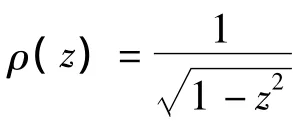
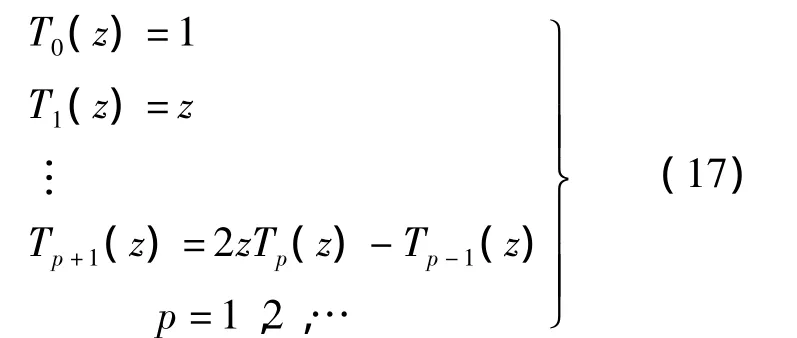
记前p阶Chebyshev正交多项式的张成子空间为Hp=span{T0(z),T1(z),…,Tp(z)},则根据函数的Chebyshev正交展开理论,对退化的功能函数G(z),有

式中

由Gauss-Chebyshev求积公式,有

式中 zk(k=1,2,…,q)为 Tq(z)的零点,可以表示为
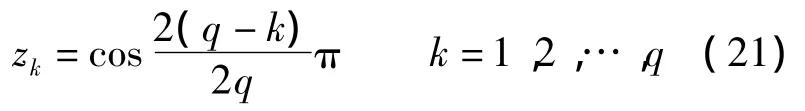
且 Ck(k=1,2,…,q)为求积系数,可以表示为
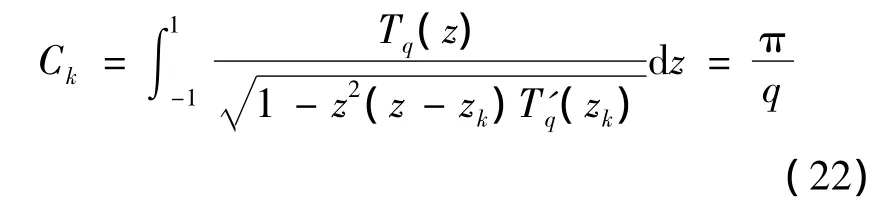
则有

因此退化功能函数可以表示为
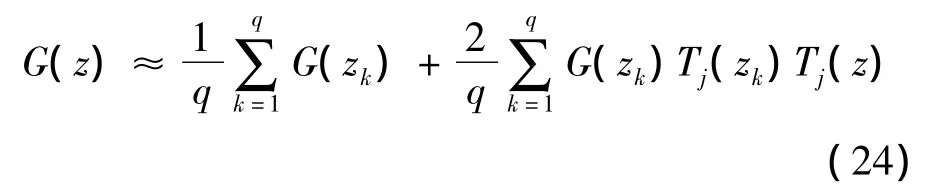
将式(24)写成矩阵形式有

式中

其中

为求解退化的功能函数G(z)的上下界,首先计算导函数 G'(z)的零点),记,计算退化功能函数在zextre中各元素处的值并以zmin和zmax分别表示G(z)的最小值点和最大值点.按照相同的处理方法,将式(14)中下标i从1~m+n遍历,并以和)分别表示第个变量变化,其余m+n-1个变量取均值下退化功能函数的最小值点和最大值点,记

则结构功能函数在给定隶属度λ下的最小值和最大值分别为

根据非概率可靠性理论,在给定隶属度λ下结构可靠度可以表示为
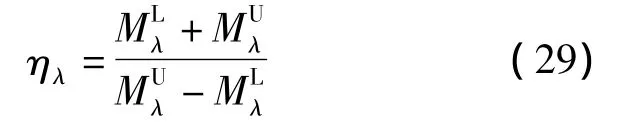
由式(29)可知,模糊非概率区间混合变量下结构可靠度具有模糊性,其模糊性是由结构模糊参数的内在模糊性传递而来.为实现结构可靠度的模糊性定量化,本文通过在区间[0,1]内遍历隶属度λ的取值拟合在模糊非概率混合变量情形下结构可靠度的隶属度函数.
3 算法分析
在给定隶属度下,基于逐维策略将结构功能函数最值计算过程转化为最值点向量的逐维确定过程,并通过结构功能函数确定其分布范围,从而根据结构非概率可靠性理论计算结构可靠度,将分别从算法精度和算法效率2个方面进行理论分析.
3.1 精度分析
实际工程结构的复杂性造成其功能函数数学形式上表现为非线性高维隐式函数,如对高层建筑进行可靠度分析时,其顶层最大位移与结构的梁、柱截面面积、截面惯性等几何特征关系不能用一个简单计算式来明确表达.对于隐式功能函数问题,代理模型已经发展成为一种有效处理方法.
传统代理模型包括响应面模型、Kriging模型、径向基函数模型及神经网络模型等,均是在设计向量的全空间范围内对精确函数进行逼近,效率和精度之间矛盾显著,尤其是对高维变量情形,即代理模型高精度要求造成计算量非常可观,而在可接受计算代价下精度有限.本文基于逐维策略在一维空间内对退化功能函数进行近似,其精度取决于Chebyshev展开式系数求解的精度和近似模型精度.对于近似模型展开式系数计算的截断误差可以表示为
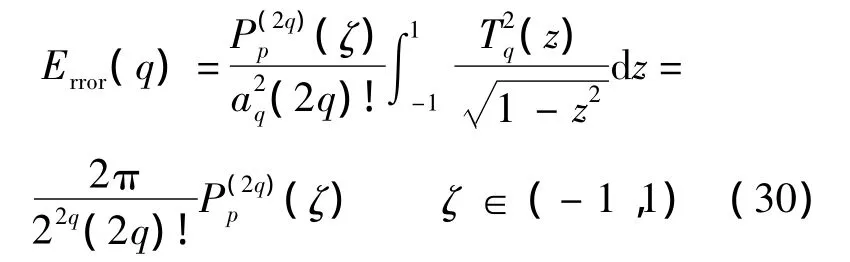
式中,q表示Gauss-Chebyshev求积节点个数;p表示Chebyshev模型的阶数.根据式(30),有

即通过求积节点个数可将给定近似模型阶数的系数求解误差控制为0.在工程问题中一般选择p=3~11,相应地可以确定求积节点个数q的取值.对于后者而言,由于在一维空间对退化功能函数进行逼近,更高阶多项式的应用使得截断误差更小,精度更高.
3.2 效率分析
对于工程复杂结构可靠性分析问题,本文算法的主要计算量为式(26)中Gcoe的有限元分析计算.在给定隶属度λ下,需要进行(m+n)(q+2)次结构有限元分析.与结构有限元计算相比,系数矩阵T及导函数G'(z)零点的求解计算量可忽略不计.在满足精度要求计算响应函数范围前提下,本文方法较优化方法计算量明显减小,尤其在结构功能函数为隐式功能函数的情况下.
值得注意的是,本文算法基于逐维策略通过确定特定范围内极值点向量而计算功能函数界限,虽针对参数向量的每维变量计算过程与效率相同,并可实现维度并行计算,但在变量空间具有很高维数的情况下,计算过程仍略显繁琐,这也将成为本文算法的改进方向之一.
4 算例与应用
4.1 管状悬臂梁结构可靠性分析
对文献[18]中如图1所示管状悬臂梁结构进行可靠性分析,其总长度为L1,内外直径分别为d1和 d2,受到外力载荷 F1,F2,F3及扭矩 T的作用.结构安全需满足条件:悬臂梁固定端圆周下表面处最大应力值σmax不超过强度S,即结构功能函数可以表示为

式中


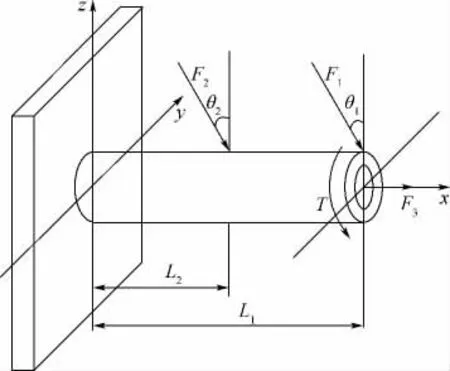
图1 管状悬臂梁结构
在分析中,悬臂梁结构参数 L1=200 mm,L2=100mm,θ1=30°,θ2=30°及 T=90N·m 为固定值.悬臂梁内外直径d1和d2因生产工艺水平限制而分布在区间范围内,有 d1∈[25.4,35.6]mm,d2∈[39,45]mm,结构强度 S 和外载荷 Fi(i=1,2,3)由统计特性可以简化为模糊参数,隶属度函数表示为
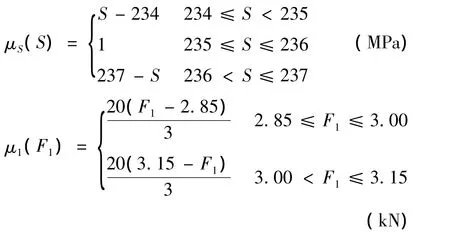
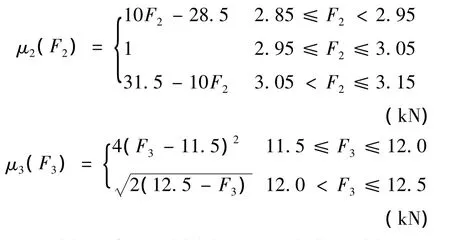
结构可靠度的模糊性是由外载荷及结构强度的内在模糊性引起的,可以通过可靠度隶属度函数予以定量化.根据本文模糊非概率可靠性分析模型,以通过9个配点计算的4阶Chebyshev多项式为代理模型,计算得出的结构可靠度隶属度函数如图2所示,其中ODMF表示隶属度函数原始数据点,FMF曲线表示拟合的隶属度曲线,OPMF表示采用优化方法求解非概率可靠度而得出的隶属度曲线.在相同计算平台上,通过Matlab数值模拟,本文方法计算时间约为0.873 0 s,以Isight平台中Pointer算法集成Matlab模拟的既有优化方法的计算时间约为103 s(未计入调用Matlab软件的时间).通过与优化方法计算得出的隶属度函数曲线相比,本文方法在有效降低计算量的同时保证了计算精度.由图2可知结构可靠度不小于1的隶属度为0.70.同时,本文所提出的模糊非概率可靠性模型可以指导含模糊非概率混合变量结构的优化设计.优化目标可选为最小化可靠度为1时的隶属度,即意味着在较低的隶属度下仍然满足结构是安全可靠的,较低的隶属度意味着生产工艺水平要求较低.

图2 管状悬臂梁结构可靠度隶属度函数
4.2 机翼结构可靠性分析
如图3所示为由2种不同材料组成的某型支线客机机翼的简化有限元模型,应用本文方法分析机翼蒙皮在不确定载荷作用下的模糊可靠度.载荷因子p和蒙皮材料强度S为区间参数,即p∈[0.95,1.05],S∈[280,283]MPa,材料弹性模量E1和E2为模糊参数,隶属度函数分别表示为

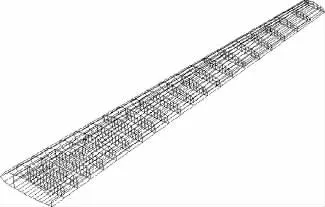
图3 机翼结构有限元模型
选择9配点4阶Chebyshev多项式代理模型,管状悬臂梁结构的隶属度分析表明本文方法能够精确高效地捕捉不同可能度水平下结构功能函数的界限值.通过本文方法计算得出的机翼蒙皮结构可靠度的隶属度函数曲线如图4所示,可靠度为1的可能度为0.35.由于有限元分析计算的复杂性,采用优化方法计算不同隶属度水平下结构功能函数的界限值的计算量难以承受,造成复杂结构模糊非概率可靠度分析的困难.然而,本文方法基于逐维策略在满足工程精度要求的前提下显著地减小了计算代价,为复杂结构模糊非概率可靠度分析及混合不确定环境下结构优化设计提供了可行途径.

图4 机翼结构可靠度隶属度函数
5 结论
针对含模糊非概率混合变量的结构可靠性分析问题,本文首先提出了逐维策略下的结构非概率可靠度最短距离模型的高效精确算法,避免了可靠度优化求解过程,提高了计算效率和精度;基于模糊数学分解原理,将结构模糊非概率可靠度分析问题等价地转化为一系列非概率可靠度分析问题,并采用所提出可靠度算法对转化后的非概率可靠度分析模型进行了求解,精确高效地计算了结构可靠度的隶属度函数;最终实现本文算法的工程应用.本文主要结论包括:
1)本文通过计算结构可靠度隶属度函数实现了结构可靠度模糊性的定量化;
2)本文提出非概率可靠度计算方法合理可行,具有计算量小且计算精度高的特点;
3)与非概率可靠度估计的优化方法相比,本文所提方法适用于具有隐式功能函数的复杂结构可靠度分析;
4)本文方法基于逐维策略提高了功能函数界限值捕捉效率,为复杂工程结构可靠度分析及后续可靠性优化设计提供了可行途径.
References)
[1] Cheng Gengdong,Xu Lin,Jiang Lei.A sequential approximate programming strategy for reliability-based structural optimization[J].Computers Structures,2006,84(21):1353 - 1367
[2] Ben-Haim Y,Elishakoff I.Convex of uncertainty in applied mechanics[M].Amsterdam:Elsevier Science,1990
[3]黄洪钟,孙占全,郭东明,等.随机应力模糊强度时模糊可靠性的计算理论[J].机械强度,2001,23(3):305-307 Huang Hongzhong,Sun Zhanquan,Guo Dongming,et al.Fuzzy reliability analysis in the case of random stress and fuzzy strength[J].Journal of Mechanical Strength,2001,23(3):305 - 307(in Chinese)
[4] Huang Hongzhong.Calculation of fuzzy reliability in the case of random stress and fuzzy fatigue strength[J].Chinese Journal of Mechanical Engineering:English Edition,2000,13(3):197 -200,223
[5] Dong Yuge,Wang Ainan.A fuzzy reliability analysis based on the transformation between discrete fuzzy variables and discrete random variables[J].International Journal of Reliability,Quality and Safety Engineering,2006,13(1):25 -35
[6] Cai K Y,Wei C Y,Zhang M L.Fuzzy variables as a basis for a theory of fuzzy reliability in the possibility context[J].Fuzzy Sets and Systems,1991,42(2):145 -172
[7] Cai K Y,WeiC Y,Zhang M L.Fuzzy states as a basis for a theory of fuzzy reliability [J].Microelectronics and Reliability,1993,33(15):2253 -2263
[8]郭书祥,吕震宙.基于可能性理论的结构模糊可靠性方法[J].计算力学学报,2002,19(1):89 -93 Guo Shuxiang,Lü Zhenzhou.A fuzzy reliability approach for structures in the possibility context[J].Chinese Journal of Computational Mechanics,2002,19(1):89 -93(in Chinese)
[9]郭书祥,吕震宙.结构可靠性分析的概率和非概率混合模型[J].机械强度,2002,24(4):524 -526 Guo Shuxiang,Lü Zhenzhou.Hybrid probabilistic and non-probabilistic model of structural reliability[J].Journal of Mechanical Strength,2002,24(4):524 -526(in Chinese)
[10] Qiu Zhiping,Wang Jun.The interval estimation of reliability for probabilistic and non-probabilistic hybrid structural system[J].Engineering Failure Analysis,2010,17(5):1142 -1154
[11] Luo Yangjun,Kang Zhan,Li Alex.Structural reliability assessment based on probability and convex set mixed model[J].Computers and Structures,2009,87(21/22):1408 -1415
[12]姜潮,刘丽新,汤一飞.一种带区间变量混合模型的结构可靠性分析方法[J].汽车工程,2012,34(8):727 -732 Jiang Chao,Liu Lixin,Tang Yifei.A structural reliability analysis method for hybrid model with interval variables[J].Automotive Engineering,2012,34(8):727 -732(in Chinese)
[13]乔心州,仇原鹰,盛英.含模糊变量和区间变量的结构可靠性优化设计方法[J].计算力学学报,2010,27(3):537-541 Qiao Xinzhou,Qiu Yuanying,Sheng Ying.Reliability-based optimization of structures with fuzzy and interval variables[J].Chinese Journal of Computational Mechanics,2010,27(3):537-541(in Chinese)
[14]李昆锋,杨自春,孙文彩.结构非概率-模糊混合可靠性分析方法[J].华中科技大学学报:自然科学版,2012,40(8):67-71 Li Kunfeng,Yang Zichun,Sun Wencai.Analyzing hybrid nonprobabilistic and fuzzy reliability of structures[J].Journal of Huazhong University of Science and Technology:Natural Science Edition,2012,40(8):67 -71(in Chinese)
[15] Zimmermann H J.Fuzzy set theory and its applications[M].Boston:Kluwer Academic Publishers,1991
[16]郭书祥,吕震宙,冯元生.基于区间分析的结构非概率可靠性模型[J].计算力学学报,2001,18(1):56 -60 Guo Shuxiang,Lü Zhenzhou,Feng Yuansheng.A non-probabilistic model of structural reliability based on interval analysis[J].Chinese Journal of Computational Mechanics,2001,18(1):56-60(in Chinese)
[17]颜庆津.数值分析[M].北京:北京航空航天大学出版社,2010 Yan Qingjin.Numerical analysis[M].Beijing:Beihang University Press,2010
[18]姜潮,张哲,韩旭.一种基于证据理论的结构可靠性分析方法[J].力学学报,2013,45(1):103 -115 Jiang Chao,Zhang Zhe,Han Xu.An evidence-theory-based reliability analysis method for uncertain structures[J].Chinese Journal of Theoretical and Applied Mechanics,2013,45(1):103-115(in Chinese)

