Improved shape hardening function for bounding surface model for cohesive soils

Andrés Nieto-Leal,Victor N.Kaliakin

aDepartment of Civil&Environmental Engineering,University of Delaware,Newark,DE 19716,USA

bDepartment of Civil Engineering,Universidad Militar Nueva Granada,Bogotá,Colombia

Improved shape hardening function for bounding surface model for cohesive soils

Andrés Nieto-Leala,b,Victor N.Kaliakina,*

aDepartment of Civil&Environmental Engineering,University of Delaware,Newark,DE 19716,USA

bDepartment of Civil Engineering,Universidad Militar Nueva Granada,Bogotá,Colombia

A R T I C L EI N F O

Article history:

Received 9 April 2013

Received in revised form

11 December 2013

Accepted 25 December 2013

Available online 4 March 2014

Constitutive model

A shape hardening function is developed that improves the predictive capabilities of the generalized bounding surface model for cohesive soils,especially when applied to overconsolidated specimens.This improvement is realized without any changes to the simple elliptical shape of the bounding surface,and actually reduces the number of parameters associated with the model by one.

©2014 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

1.Introduction

Since the late 1970’s,the bounding surface concept has been successfully used to simulate the response of cohesive soils.A form of a bounding surface/yield surface model was brief l y mentioned by Mrŏz et al.(1978)and subsequently fully developed within the framework of critical state soil mechanics by Mrŏz and his coworkers(Mrŏz et al.,1979;Pietruszczak and Mrŏz,1979).

A direct bounding surface formulation for isotropic soil plasticity was qualitatively presented by Dafalias(1979a)for the case of zero elastic range and in conjunction with implied loading surfaces and a quasi-elastic range(Dafalias,1979b).The latter version of the model was subsequently developed fully within a two-(Dafalias and Herrmann,1980,1982a)and three-invariant framework (Dafalias and Herrmann,1982b;Dafalias et al.,1982),synthesized (Dafalias and Herrmann,1986),and then subsequently simplif i ed (Kaliakin and Dafalias,1989).Anandarajah and Dafalias(1986) developed a version of the model suitable for simulating the response of anisotropically consolidated cohesive soils that served as a basis for subsequent enhanced anisotropic bounding surface models(Ling et al.,2002;Jiang et al.,2012).A time-dependent version of the model for isotropic cohesive soils was proposed (Dafalias,1982a,b,1986a),ref i ned and implemented by Kaliakin (1985),andformallypresentedandverif i ed(Kaliakinand Dafalias,1990a,b).

The predictive capabilities of bounding surface models for cohesive soils have typically been assessed by comparing numerical results with data obtained from laboratory tests.The majority ofthesetestswereperformedunderaxisymmetrictriaxial compression and extension stress states.In a few instances,more complex stress states were considered.This included the centrifuge modeling of the f i lling and emptying of an oil storage tank (Shen et al.,1986),the simulation of a caisson-retained sand island in the Canadian Beaufort Sea(Kaliakin et al.,1990),and sundry simulations of true triaxial test results under drained conditions (Kaliakin and Pan,2002;Kaliakin,2005;Anantanasakul and Kaliakin,2012;Jiang et al.,2013).

In the most recent study of the true triaxial response of clays, Kaliakin and Nieto-Leal(2012)investigated the existence of critical states under three-dimensional stress states.The results of this investigation indicated the possible need for a more ref i ned failure criterion,as well as for more accurate stress-strain simulations under general states of stress.

This paper presents an improved shape hardening function that increases the accuracy of stress-strain simulations for moderately to heavily overconsolidated soils.This added accuracy is realized without any changes to the simple elliptical shape of the bounding surface(Kaliakin and Dafalias,1989),and actually reduces thenumber of parameters associated with the model by one.In order to better illustrate the effect of an improved shape hardening function on its predictive capabilities,in this paper the generalized bounding surface formulation(Kaliakin and Nieto-Leal,2013)is specialized to a form suitable for isotropic cohesive soils.

2.General aspects of elastoplasticity

This section presents some general aspects related to a rateindependent elastoplastic formulation.These serve as a basis against which to contrast the bounding surface concept that is presented in the next section.

The existence of a smooth,convex yield surface that separates the regions of purely elastic and plastic response in stress space is assumed.It is completelyenclosed bya smooth loading surface that is not necessarily identical with the yield surface(Eisenberg and Phillips,1971).The loading surface is analytically de fi ned by

Stress increments directed outward from the loading surface produce plastic deformations and are termed loading increments; those tangential to the surface and those directing inwards are termed neutral and unloading increments,respectively,and produce no plastic deformations.

A scalar loading indexLis def i ned as follows:

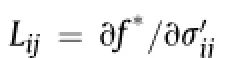
Imposing the requirement of continuous material response with respect to a changing direction of dσacross neutral loading (Dafalias and Popov,1976),the incremental plastic constitutive relations are given by

3.The bounding surface concept

In this section,some general aspects of the bounding surface concept associated with rate-independent plasticity are presented in order to facilitate the subsequent discussion of the improved shape hardening function.Further details pertaining to the bounding surface concept were given in Dafalias(1986b).

The bounding surface concept was motivated by the observation that any stress-strain curve for monotonic loading,or for monotonic loading followed by reverse loading,eventually converges to certain well-def i ned“bounds”in the stress-strain space (Dafalias and Popov,1975;Krieg,1975).These bounds cannot be crossed but may change position in the process of loading.In addition,the rate of convergence,expressed by means of the plastic modulus,depends upon the“norm”or“distance”(in a proper metric space)between the current state and a corresponding“bounding”state.

The evolution of the bounding state and the interrelation with the actual state by means of the distance offers a general framework for the development of realistic elastoplastic constitutive models.A microscopic interpretation of the bounding state can be made by associating it with the packing history incurred by soil particles(Mrŏz et al.,1978).However,because in the process of deformation the bounding state evolves,it is not identical to a limit state for metals,or to a critical state(where unrestricted f l ow occurs)for soils.

For the development of constitutive models,the simplest way to describe the bounding state is by means of the concept of a bounding surface in stress space(Dafalias,1981).In models appropriate for soils,the bounding surface always encloses the origin and is origin-convex,i.e.any radius emanating from the origin intersects the surface at only one point(Fig.1).

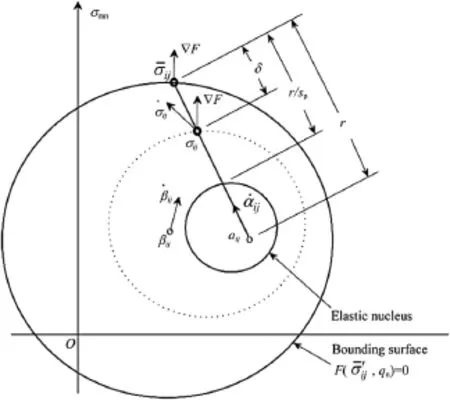
Fig.1.Schematic illustration of the bounding surface and radial mapping rule in multiaxial space.

The essence of the bounding surface concept is the hypothesis that plastic deformations can occur for stress states either within or on the bounding surface.Thus,unlike classical yield surface elastoplasticity,the plastic states are not restricted only to those lying on a surface.This fact has proven to be a great advantage of the bounding surface concept.

In an effort to simplify earlier formulations,Dafalias(1979a) introduced a very simple“radial mapping”rule that does not require an explicit def i nition of a yield surface.A similar mapping rule had been introduced earlier by Hashiguchi and Ueno(1977). The radial mapping rule combines simplicity and ease of numerical implementation,and has been shown to accurately predict the rate-independent elastoplastic behavior of cohesive soils(Dafalias and Herrmann,1980,1982a,b;Dafalias et al.,1982;Dafalias and Herrmann,1986).For these reasons,the radial mapping rule is used in the present development.

In the resulting bounding surface model as shown schematically in Fig.1,it is assumed that the projection centerαijlies always within a convex bounding surface and never crosses it.Theαijmay be thought of as a second back-stress in addition to the geometric centerβijof the bounding surface.Theαijevolves according to a proper rate equation,and is one of the internal variables.It does not,however,enter into the analytical expression for the bounding surface.Using theαijas the projection center,the“image”stress is obtained by the radial projection of the actual stress onto the surface according to

4.Formulation for isotropic cohesive soils

The elastoplastic bounding surface formulation developed to this point is quite general and it is only the concept of effective stress that makes it appropriate for soils as well.Any type of material symmetries can now be incorporated into the formulation by properly def i ning the elastic moduli and rendering the bounding surface,a function of proper invariant quantities of the effective stress and the internal variables.In this section the generalized bounding surface formulation(Kaliakin and Nieto-Leal,2013)is specialized for isotropic cohesive soils.

4.1.Stress invariants

whereS=(sijsjkski/3)1/3is the third root of the third deviatoric stress invariant.

4.2.Hardening of the surface

whereeinrepresents the initial total void ratio corresponding to the reference conf i guration with respect to which engineering strains are measured.For natural strains,einrepresents the current total void ratio.

It is convenient to relate the evolution of the bounding surface to the inelastic void ratio through the value ofI0,which represents the point of intersection of the bounding surface with the positive partof theI1-axis in invariant stressspace(Fig.2),and measures the amount of preconsolidation of the soil.For an isotropic soil consolidated isotropically(i.e.along theI1-axis),only volumetric strains are generated.This fact,in conjunctionwith Eq.(15),implies thatI0must depend only onep.Therefore,an expression for dI0=dep,necessary for the analytical description of the hardening behavior,is now sought.

Although the hardening of the bounding surface can be described analytically in a number of ways,past practice has employed aspects of critical state soil mechanics(Schof i eld and Wroth,1968).Using such an approach leads to the following expression(Dafalias and Herrmann,1986):

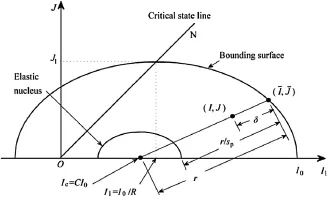
Fig.2.Schematic illustration of elliptical bounding surface and radial mapping rule in stress invariants space.

where the critical state parametersλandκdenote the slopes of the isotropic consolidation and swell/recompression lines,respectively, in a plot of void ratio versus the natural logarithm ofI1,andILis a nonzero limit value ofI1such that forI1＜ILthe relation betweenI1and the elastic part of the void ratio(ee)changes continuously from logarithmic tolinear(Dafalias and Herrmann,1986).In this manner, the singularity of the elastic stiffness nearI1=0(resulting from excessive material softening)is removed.It is important to note thatILisnota model parameter;its value is typically taken equal to one-third of the atmospheric pressurePa.

The elastic response is assumed to be isotropic.It is further assumed to be independent of the rate of loading,and to be unaltered by inelastic deformation.The consequence of adopting aspects of critical state soil mechanics is that the elastic bulk modulus becomes a function ofI1according to

The elastic shear modulusGis either def i ned independently,or is computed fromKand a specif i ed value of Poisson’s ratio(ν). Based upon the above discussion,and recalling Eq.(6),the bounding surface is def i ned analytically by

Eq.(18)can assume many specif i c forms provided certain conditions regarding the chosen shape are satisf i ed.A specif i c analytical expression for the bounding surface is presented in Section 6.

4.3.Specialization of the formulation

The radial mapping rule given by Eq.(7)is specialized by explicitly def i ning the projection centerαij,as well as its evolution. Since isotropy is assumed,the projection center must be an isotropic tensor with a principal valueI1=Icon theI1-axis in invariant stress space,i.e.αij=1/3δijIc(Dafalias and Herrmann, 1986).In past applications of the bounding surface plasticity model for cohesive soils,the projection center was f i xed at the stress origin(I1=J=0).Motivated by the less-than-satisfactory analytical predictions for samples having a large initial degree of overconsolidation,Dafalias(1982a)proposed a generalization of earlier forms of Eq.(7)that def i nes an image stress state given by

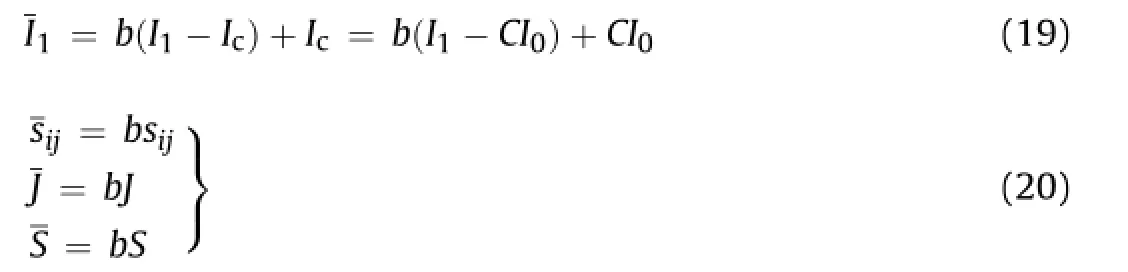
whereCis a dimensionless model parameter(0≤C＜1).

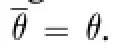
where Eq.(16)was used.

5.The failure criterion

For a specif i c value of the Lode angleθ,the failure surface reduces to a straight line that is assumed to coincide with the critical state line(Schof i eld and Wroth,1968).InI1-Jspace,the slope of the critical state line is denoted byN.The variation ofNwithθis described as follows:

TheNe=N(-π/6)andNc=N(π/6)are the values ofN(θ) associated with axisymmetric triaxial extension and compression, respectively.

The dimensionless functiong(θ,k)must take on the valuesg(-π/ 6,k)=kandg(π/6,k)=1.A simple form of this function,attributed to Gudehus(1973)and Zienkiewicz and Pande(1977)and then used(Dafalias and Herrmann,1982b,1986;Dafalias et al.,1982)in conjunction with bounding surface models for clays,is

Although the accuracy of Eq.(23)for representing the variation of the failure criterionwithθfor three-dimensional stressstates has recently been questioned(Kaliakin and Nieto-Leal,2012),it is nonetheless used herein.

6.Specif i c form of the bounding surface

The analytical def i nition of the bounding surface,described in general by Eq.(18),is assumed to be an ellipse(Kaliakin and Dafalias,1989):

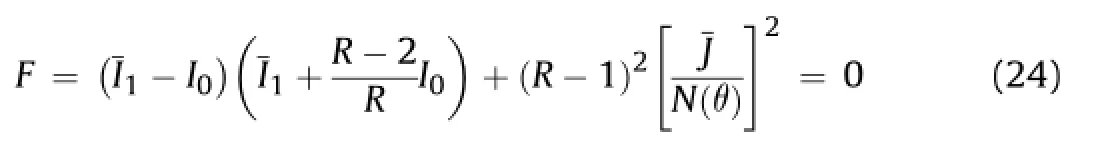
whereR≥2.0 is a dimensionless model parameter that controls the shape of the elliptic surface.In particular,larger values ofRimply a“f l atter”surface.Fig.2 shows a section of this surface for a given value ofθ,along with its associated parametersCandR.The failure surfaceN(θ)is given by Eq.(22).

7.The shape hardening function

The hardening function＾Hdef i nes theshapeof the response curves during inelastic hardening(or softening)for pointswithinthe bounding surface(i.e.forδ＞0).It relates the plastic modulusKpto its“bounding”valueKpin the following general manner:

7.1.Composite form of the bounding surface

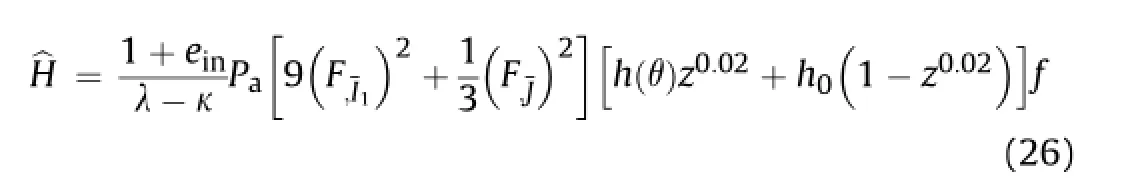
wherez=J/J1=JR/NI0is a dimensionless variable,andfis equal to unity.The term 1+einis included in Eq.(26)because of its presence in the expression forKpin Eq.(21).The quantityPais the atmospheric pressure;it is included to giveHthe proper units of stress cubed.The quantity(λ-κ)is introduced into Eq.(26)only for similarity to the aforementioned Eq.(21)forKp.The quantityh0represents the hardening parameter for states in the immediate vicinity of theI1-axis(i.e.forz≈0).

The f i rst bracketed quantity in Eq.(26)was required to preserve continuity of the stress rate-strain rate relation in the composite form of the bounding surface(Dafalias and Herrmann,1986). Subsequent experience has shown that even for the simpler single ellipse version of the surface(Kaliakin and Dafalias,1989)that is further discussed in the following section,this quantity should be retained in the functional form for＾H.

The dimensionless quantityh(θ)def i nes the degree of hardening for points within the bounding surface,except those within the immediate vicinity of theI1-axis wherez→0.Of all the hardening quantities,h(θ)has the most fundamental and signif i cant role.It is a function of the Lode angleθand varies in magnitude from avalue ofhc=h(π/6)(corresponding to a state of triaxial compression)to a value ofhe=h(-π/6)(corresponding to a state of triaxial extension).More precisely,this interpolation is given by

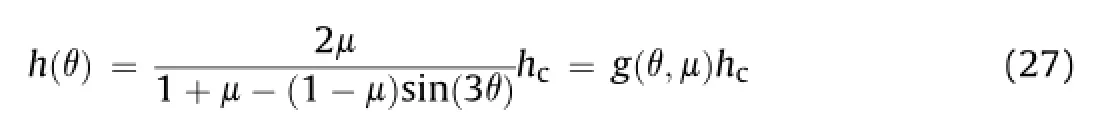
whereμ=he/hc.

The quantityh0is included in the formulation to ensure continuity when the stress point crosses theI1-axis,thereby improving numerical behavior in this region.For simulations involving both triaxial compression and extension,it is very important to properly computeh0so as to ensure a relatively smooth transition betweenhcandhe.Since it is typically set equal to theaverageofhcandhe,h0does not explicitly enter into the calibration process for the model parameters.

In the second bracketed quantity in Eq.(26),the termz0.02may be thought of as a weighting factor with respect toh(θ)andh0.The small exponent(0.02)onzrenders the quantityz0.02≈1,even for small nonzero values ofz.Thus,for stress states off theI1-axis(e.g. forJ≠0),h(θ)will be the predominant term in the second bracketed quantity.For hydrostatic states of stress(i.e.J=0)this quantity will be equal toh0.

Finally,Dafalias and Herrmann(1986)assumed the following expression for＾f（δ）appearing in Eq.(25):

wheresp(sp≥1)is a model parameter that def i nes the size of the“elastic nucleus”(Fig.2),andbis as def i ned in Eq.(7).Ifsp=1,the elastic nucleus reduces to a point,resulting in elastoplastic response being predicted within the entire bounding surface.

7.2.Single ellipse form of the bounding surface

In an effort to simplify the aforementioned composite form of the bounding surface,a simpler formulation for isotropic cohesive soils consisting of a single ellipse was developed(Kaliakin and Dafalias,1989).The associated functional form of＾His again given by Eq.(26).Although the adoption of a single ellipse simplif i es the explicit def i nition of the bounding surface,it requires the modif ication of previous functional forms of＾H.More precisely,if a single ellipse is used instead of a hyperbola associated with the composite form of the surface(which is closer to the critical state line),undesirably high levels ofJwill be attained at moderate to large overconsolidation ratios(OCRs).To prevent this from occurring,the following functional form off(in Eq.(26))was added to the expression for＾H(Kaliakin and Dafalias,1989):

7.3.Improved shape hardening function

In order to further improve the predictive capabilities of the isotropic bounding surface model employing a single ellipse,Eq. (26)was modif i ed by replacing Eq.(29)with the following expression:

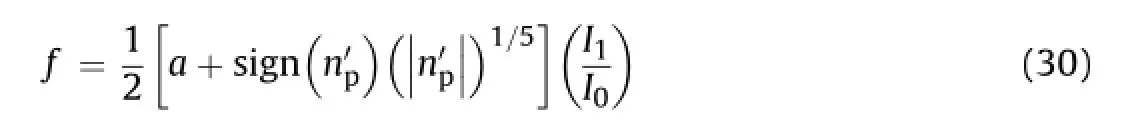
Comparing Eqs.(29)and(30),it is evident that the model parameterwis no longer present in the latter.Finally,the term(I1/I0)has been added to Eq.(30)so as to better account for the overconsolidation ratio in the functional form of＾H.

To facilitate the discussion off,the following triaxial space parameter is def i ned:η=q/p＇.The actual state need not,however, be triaxial.The quantitynpthus ranges in value from+1(corresponding toη=0 andp＇＞0)to-1(forη=0 andp＇＜0).When the“image”stress is at the intersection of the bounding surface with the critical state line(i.e.whenη=M),np=0.

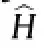
8.Assessment of predictive capabilities

In this section,the predictive capabilities of the isotropic bounding surface model consisting of a single ellipse with the improved＾Hgiven by Eqs.(26)and(30)are assessed.This assessment is realized by comparing this form of the model to experimental results,and to simulations obtained using＾Hgiven by Eq. (26)withfeither equal to unity(and thus associated with the composite form of the bounding surface),orequal to the expression given in Eq.(29)(and thus associated with the original form of the bounding surface consisting of a single ellipse).

The following model parameters are associated with both versions of the model:the critical state parameters(λ,κ,McandMe), the elastic parameters(shear modulusGor Poisson’s ratioν),the bounding surface conf i guration parameter(R),the projection center parameter(C),the elastic nucleus parameter(sp),and the shape hardening parameters(hcandhe).In addition,the composite form of the bounding surface model requires values for the parameterRe(that def i nes the shape of the f i rst ellipse in extension),the parametersAcandAe(associated with the hyperbola,in triaxial compression and extension,respectively),as well as the parameterT(that def i nes the second,or tension ellipse).For＾Hwithfgiven by Eq.(29),the parametersaandwmust also be included.Finally,the improved＾Hwithfgiven by Eq.(30)only requires the single additional parametera.

8.1.Simulation of undrained shearing of a kaolin mixture

The soil used in the f i rst set of simulations is a laboratory prepared mixture of two commercial grades of kaolin(liquid limit=37 and plasticity index=8).Shen et al.(1986)used this soil in centrifuge experiments that served to validate the predictive capabilities of the bounding surface model for isotropically consolidated cohesive soils.For this purpose,the kaolin mixture was originally characterized using the composite form of the bounding surface consisting of two ellipses and one hyperbola.It is thus of interest to compare this previous simulation with similar ones obtained using the single ellipse version of the model.

In addition to standard consolidation tests,a series of six isotropically consolidated undrained tests were performed using an axisymmetric triaxial device.Three tests were performed in compression and three in extension.TheOCRsfor each group of tests were equal to 1.0,2.0 and 6.0.

Values for the traditional critical state parameters were taken from Shen et al.(1986).In particular,λ=0.0745,κ=0.0105,Mc=1.35,Me=0.90,andν=0.22.For the version of the model employing a composite form of the bounding surface,the values of the parametersRc=3.05 andRe=1.71 were determined bymatching the shape of the undrained stress paths in triaxial compression and extension,respectively.The value of the projection center parameterC=0.485 was determined fromthe shapes of all six undrained stress paths.The values of the bounding surface parameters that determine the size of the hyperbola(Ac=0.175 andAe=0.149),as well as the hardening parametershc=11.0 andhe=9.63 were determined by matching the results forOCRequal to 6.0 in triaxial compression and extension.Using the above parameter values in conjunction with the composite form of the bounding surface,the undrained simulations shown in Fig.3a-c were generated.From these f i gures,it is evident that the simulations obtained using the composite form of the bounding surface are in very good agreement with the experimental results.

The simulations were next repeated using the single ellipse version of the model.The values of the parametersλ,κ,Mc,Meandν were unchanged from those used in conjunction with the composite form of the surface.The single value of the bounding surface parameterRnow applies to both triaxial compression and extension.As such,some compromise in the simulative capabilities is expected.After some trial analyses,it was determined that lettingR=3.05 gave the best simulations of undrained results.Since it is largely determined by the shapes of the undrained stress paths (and applies for both triaxial compression and extension),the value of the projection center parameterCwas unchanged from that used in conjunction with the composite form of the bounding surface. The values for the hardening parametershcandhewere likewise unchanged from those in the composite form of the bounding surface.The values of the parametersAc,AeandTno longerapply to the single ellipse version of the model.Instead the hardening parametersaandw,that appear in Eq.(29),must be used.Based on past experience,values of 1.20 and 5.0 were used foraandw, respectively.Using these parameter values,undrained simulations similar to those shown in Fig.3a-c were generated and shall be assessed below.

Finally,the simulations were again performed using the single ellipse version of the model,only employing a modif i ed shape hardening function of Eq.(26)withfgiven by Eq.(30).The values of the parametersλ,κ,Mc,Me,ν,R,C,sp,hcandhewere unchanged from those used in conjunction with the previous simulations employing the single ellipse form of the bounding surface.The parameteranow is equal to 7.0,and the parameterwis no longer required.Using these parameter values,undrained simulations similar to those shown in Fig.3a-c were generated.To better understand the effect of using the improved shape hardening function on the simulations,the material response in triaxial compression is considered.In the legends of Fig.4a-c,the designation“(f=1.0)”refers to the composite form of the bounding surface,and“(ffrom Eq.(29))”and“(ffrom Eq.(30))”refer tothe single ellipse version of the bounding surface withfgiven by Eqs.(29)and(30),respectively.From Fig.4a-c,it is evident that the improved shape hardening function withfgiven by Eq.(30)gives results that are closer to the experimental ones than those obtained using either the composite form of the bounding surface(i.e.forf=1.0),or those obtained using Eq.(29).In short,even though the improved＾Hrequires one less model parameter as compared to the function that uses Eq.(29),it nonetheless produces more accurate simulations.

8.2.Simulation of lower Cromer till response

The single ellipse version of the isotropic bounding surface model was also used to simulate the response of isotropically consolidated lower Cromer till(LCT),based on the work of Gens (1982).LCT is classif i ed as a low-plasticity sandy silty-clay(liquid limit=25 and plasticity index=13),with the main clay minerals being calcite and illite.The tests on LCT were all performed onsamples consolidated from a slurry with an initial water content of 31%.Although the bounding surface model has traditionally been applied to rather soft clays with larger liquid limits and plasticity indices,the choice of LCT is motivated by its use in the verif i cation of other clay models(Dafalias et al.,2006).

Fig.3.Simulations for triaxial compression(TC)and triaxial extension(TE)for the UCD kaolin mixture obtained using the“composite”form of the bounding surface.uis the pore water pressure.

Valuesforthetraditionalcriticalstateparameterswere computed from the data of Gens(1982).In particular,λ=0.066, κ=0.0077,Mc=1.18,Me=0.86,andν=0.20.Avalue of 2.30 for the parameterRdef i ning the shape of the elliptical bounding surface was determined from the experimental undrained stress paths for normally consolidated samples in triaxial compression and extension.A value of 0.52 for the projection center parameterCwas determined by the shapes of the undrained stress paths for lightly overconsolidated samples.The rather“stiff”nature of these undrained stress paths required a value of 2.0 for the elastic nucleus parametersp.Finally,the values ofhc=1.0 andhe=5.0 were determined by matching the stress-strain response of overconsolidated samples.For the version of the model withfgiven by Eq.(29),values ofa=6.0 andw=5.0 were determined so as to best match the results of moderately and heavily overconsolidated samples.For the version of the model using the improved＾Hwithfgiven by Eq.(30)the value ofhcneeded to be increased to 5.0,and a value ofaequal to 2.50 was found to give the best match with experimental results.Fig.5a and b compares the numerical and experimental undrained stress paths and stress-strain response, respectively,using the improved version.

Fig.4.Comparison of model simulations in triaxial compression for the UCD kaolin mixture withOCR=2.0 andOCR=6.0 obtained using the“composite”form of the bounding surface(f=1.0),fgiven by Eq.(29),andfgiven by Eq.(30),respectively.

Fig.5.Simulations for triaxial compression(TC)and triaxial extension(TE)for LCT obtained using the single ellipse form of the bounding surface withfgiven by Eq.(30).

As noted in the previous simulations of the kaolin mixture,the improved shape hardening function primarily affects the material response at highOCRs.Thus,in order to better investigate the effect using the improved shape hardening function,Fig.6a compares the undrained stress paths forOCRs equal to 4,10 and 20.As evident from this f i gure,the improved＾Hslightly improves the simulated undrained stress paths at higherOCRs.Fig.6b compares the deviator stress-axial strain response for the sameOCRs.It is evident that the improved＾Hgives somewhat more accurate stress-strain paths than for the version of the function that uses Eq.(29).It is important to note that this is achieved with one less model parameter.

Fig.6.Comparison of model simulations for LCT withOCR=4,10 and 20 obtained using the single ellipse form of the bounding surface withfgiven by Eqs.(29)and(30).

9.Conclusion

The use of an improved shape hardening function has been shown to accurately simulate the stress-strain response for overconsolidated cohesive soils.This has been demonstrated under both axisymmetric triaxial compression and extension states of stress.The use of an improved shape hardening function is a far simpler way in which to improve the simulated response of cohesive soils as compared to choosing a different,and typically more complex,analyticalexpressionfortheboundingsurface. Furthermore,this function actually reduces by one the number of parameters associated with the model.

Conf l ict of interest

We wish to con fi rm that there are no known con fl icts of interest associated with this publication and there has been no signi fi cant fi nancial support for this work that could have in fl uenced its outcome.

Acknowledgment

The f i rst author’s graduate studies are supported by the Fulbright Colombia-Colciencias Scholarship and Universidad Militar Nueva Granada.This support is gratefully acknowledged.

Anandarajah A,Dafalias YF.Bounding surface plasticity iii:application to anisotropic cohesive soils.Journal of Engineering Mechanics,ASCE 1986;112(12): 1292-318.

Anantanasakul P,Kaliakin VN.Simulations of 3-D drained behavior of normally consolidated clay using elastoplastic models.In:GeoCongress,vol.GSP 225. ASCE;2012.pp.1076-85.

Dafalias YF.A bounding surface plasticity model.In:Proceedings of the Seventh Canadian Congress of Applied Mechanics.Sherbrooke,Canada;1979.pp.89-90.

Dafalias YF.A model for soil behavior under monotonic and cyclic loading conditions.In:Transactions of the Fifth International Conference on SMIRT,vol.1. Berlin,Germany;1979b.(Division K1/8):1-9.

Dafalias YF.The concept and application of the bounding surface in plasticity theory.In:IUTAM symposium on physical non-linearities in structural analysis. Senlis,France:Springer Berlin Heidelberg;1981.pp.56-63.

Dafalias YF.Bounding surface elastoplasticity viscoplasticity for particulate cohesive media.In:IUTAM symposium on deformation and failure of granular materials. Rotterdam:A.A.Balkema;1982a.pp.97-107.

Dafalias YF.On rate dependence and anisotropy in soil constitutive modeling.In: Results of the International Workshop on Constitutive Relations for Soils. Grenoble,France:A.A.Balkema;1982b.pp.457-62.

Dafalias YF.On elastoplasticity-viscoplasticity constitutive modelling of cohesive soils.In:Geomechanical Modelling in Engineering Practice.Rotterdam:A.A. Balkema;1986a.pp.313-30.

Dafalias YF.Bounding surface plasticity.I:mathematical foundation and the conceptofhypoplasticity.JournalofEngineeringMechanics,ASCE 1986b;112(9):966-87.

Dafalias YF,Herrmann LR.A bounding surface soil plasticity model.In:Proceedings of the International Symposium on Soils under Cyclic and Transient Loading. Swansea:A.A.Balkema;1980.pp.335-45.

Dafalias YF,Herrmann LR.Bounding surface formulation of soil plasticityIn Soil mechanics transient and cyclic loads.Chichester:John Wiley and Sons,Inc.; 1982a.pp.253-82.

Dafalias YF,Herrmann LR.A generalized bounding surface constitutive model for clays.In:Application of Plasticity and Generalized Stress-strain in Geotechnical Engineering.New York:ASCE;1982b.pp.78-95.

Dafalias YF,Herrmann LR.Bounding surface plasticity ii:application to isotropic cohesive soils.Journal of Engineering Mechanics,ASCE 1986;112(12):1263-91.

Dafalias YF,Popov EP.A model of nonlinearly hardening materials for complex loadings.Acta Mechanica 1975;21(3):173-92.

Dafalias YF,Popov EP.Plastic internal variables formalism of cyclic plasticity.Journal of Applied Mechanics,ASME 1976;98(4):645-51.

Dafalias YF,Herrmann LR,DeNatale JS.The bounding surface plasticity model for isotropic cohesive soils and its application.In:Results of the International Workshop on Constitutive Relations for Soils,Grenoble,France.Rotterdam:A.A. Balkema;1982.pp.273-87.

Dafalias YF,Manzari MT,Papadimitriou AG.Saniclay:simple anisotropic clay plasticity model.International Journal for Numerical and Analytical Methods in Geomechanics 2006;30(12):1231-57.

Eisenberg MA,Phillips A.A theory of plasticity with non-coincident yield and loading surfaces.Acta Mechanica 1971;11(3-4):247-60.

Fung YC.Foundations of solid mechanics.Englewood Cliffs,NJ:Prentice Hall;1965.

Gens A.Stress-strain and strength of a low plasticity clay.PhD Thesis.London: Imperial College,London University;1982.

Gudehus G.Elastoplastische stoff l eichungen für trockenen sand.Ingenieur-Archiv 1973;42(3):151-69.

Hashiguchi K,Ueno M.Elasto-plastic constitutive laws of granular materials.In:9th International Conference on Soil Mechanics and Foundation Engineering, Constitutive Equations of Soils(specialty session 9).Tokyo,Japan:Japanese Society of Soil Mechanics and Foundation Engineering;1977.pp.73-82.

Jiang J,Ling HI,Kaliakin VN.An associative and non-associative anisotropic bounding surface model for clay.Journal of Applied Mechanics,ASME 2012;79(3):031010.http://dx.doi.org/10.1115/1.4005958.

Jiang J,Ling HI,Kaliakin VN.Simulation of natural Pisa clay using an enhanced anisotropic elastoplastic bounding surface model.Journal of Applied Mechanics, ASME 2013;80(2):024503.http://dx.doi.org/10.1115/1.4007964.

Kaliakin VN.Bounding surface elastoplasticity-viscoplasticity for clays.PhD Thesis. Davis,California:University of California,Davis;1985.

Kaliakin VN.Assessment of predictive capabilities of bounding surface model for cohesive soils under complex stress paths.In:Proceedings of McMat Mechanics and Materials Conference(CD-ROM).LA,Baton Rouge;2005.

Kaliakin VN,Dafalias YF.Simplif i cations to the bounding surface model for cohesive soils.International Journal for Numerical and Analytical Methods in Geomechanics 1989;13(1):91-100.

Kaliakin VN,Dafalias YF.Theoretical aspects of the elastoplastic-viscoplastic boundingsurfacemodelforcohesivesoils.SoilsandFoundations 1990a;30(3):11-24.

Kaliakin VN,Dafalias YF.Verif i cation of the elastoplastic-viscoplastic bounding surface model for cohesive soils.Soils and Foundations 1990b;30(3):25-36.

Kaliakin VN,Nieto-Leal A.Investigation of critical states and failure in true triaxial tests of clay.In:The Second International Symposium on Constitutive Modeling of Geomaterials:advances and new applications.Heidelberg:Springer;2012. pp.185-91.

Kaliakin VN,Nieto-Leal A.Towards a generalized bounding surface model for cohesive soils.In:Proceedings of the 5th Biot Conference on Poromechanics (BIOT-5).Vienna,Austria:ASCE;2013.pp.1011-20.

Kaliakin VN,Pan Z.Assessment of 3-D predictive capabilities of bounding surface model for cohesive soils.In:Proceedings of the 14th U.S.National Congress on Theoretical and Applied Mechanics(CD-ROM).Blacksburg,VA;2002.

Kaliakin VN,Muraleetharan KK,Dafalias YF,Herrmann LR,Shinde SB.Foundationresponse predictions below caisson-retained island.Journal of Geotechnical Engineering,ASCE 1990;116(9):1291-308.

Krieg RD.A practical two surface plasticity theory.Journal of Applied Mechanics, ASME 1975;42(3):641-6.

Ling HI,Yue D,Kaliakin VN,Themelis NJ.An anisotropic elasto-plastic bounding surface model for cohesive soils.Journal of Engineering Mechanics,ASCE 2002;128(7):748-58.

Manzari MT,Nour MA.On implicit integration of bounding surface plasticity models.Computers and Structures 1997;63(3):385-95.

Mrŏz Z,Norris VA,Zienkiewicz OC.An anisotropic hardening model for soils and its application to cyclic loading.International Journal for Numerical and Analytical Methods in Geomechanics 1978;2(3):203-21.

Mrŏz Z,Norris VA,Zienkiewicz OC.Application of an anisotropic hardening model in the analysis of elastoplastic deformation of soils.Geotechnique 1979;29(1): 1-34.

Pietruszczak S,Mrŏz Z.Description of anisotropy of naturallyk0-consolidated clays. In:Proceedings of the Euromechanics Colloquium,vol.115.Villa-de-Lans, France:Kluwer Academic Publishers;1979.

Schof i eld AN,Wroth CP.Critical state soil mechanics.London:McGraw-Hill Book Co.,Inc.;1968.

Shen CK,Sohn J,Mish K,Kaliakin VN,Herrmann LR.Centrifuge consolidation study for purposes of plasticity theory validation.In:Consolidation of Soils:Testing and Evaluation ASTM STP,vol.892.ASTM;1986.pp.593-609.

Zienkiewicz OC,Pande GN.Chapter 5:in f i nite elements in geomechanics.London: Wiley-Interscience;1977.pp.179-90.

A.Nieto-Lealearned his Bachelor Degree in Civil Engineering from Universidad Militar Nueva Granada,Bogotá, Colombia and his Master of Science in Geotechnical Engineering from Universidad de los Andes,Bogotá,Colombia. After f i nishing his graduate program in Geotechnical Engineering,he started working as a research assistant at Universidad Militar Nueva Granada and has been involved in teaching activities there since 2007.Currently,he is pursuing his PhD at University of Delaware supervised by ProfessorVictor N.Kaliakin.Hisresearchf i elds are computational geomechanics and constitutive modeling of geomaterials.Presently,he is studying the micro-and macroscopic response of saturated cohesive soils subjected tocyclic/dynamicloadingsuchasearthquakes,and improving the bounding surface model to be able to better simulate such response for normally and overconsolidated soils,including post-cyclic behavior.

*Corresponding author.Tel.:+1(302)831 2409.

E-mail addresses:andres.nieto@unimilitar.edu.co(A.Nieto-Leal),kaliakin@udel. edu(V.N.Kaliakin).

Peer review under responsibility of Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.

Bounding surface plasticity

Shape hardening function

Clay