A review of discrete modeling techniques for fracturing processes in discontinuous rock masses

A.Lisjak,G.Grasselli

Department of Civil Engineering,University of Toronto,Toronto M5S 1A4,Canada

A review of discrete modeling techniques for fracturing processes in discontinuous rock masses

A.Lisjak,G.Grasselli*

Department of Civil Engineering,University of Toronto,Toronto M5S 1A4,Canada

A R T I C L E I N F O

Article history:

Received 15 October 2013

Received in revised form

17 December 2013

Accepted 5 March 2014

Available online 14 March 2014

Rock fracturing

The goal of this review paper is to provide a summary of selected discrete element and hybrid f i nitediscreteelement modelingtechniques thathaveemergedinthe f i eldofrockmechanicsassimulationtools for fracturing processes in rocks and rock masses.The fundamental principles of each computer code are illustrated with particular emphasis on the approach specif i cally adopted to simulate fracture nucleation and propagation and to account for the presence of rock mass discontinuities.This description is accompaniedbyabriefreviewofapplicationstudiesfocusingonlaboratory-scalemodelsofrockfailureprocesses and on the simulation of damage development around underground excavations.

©2014 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

1.Introduction

A large body of experimental research shows that the failure process in brittle rocks under compression is characterized by complicated micromechanical processes,including the nucleation, growth and coalescence of microcracks,which lead to strain localization in the form of macroscopic fracturing(Lockner et al., 1991;Benson et al.,2008).The evolution of micro-cracking,typicallyassociated with the emission of acoustic energy(AE),results in a distinctive non-linear stress-strain response,with macroscopic strain softening commonly observed under low-conf i nement conditions(Brace et al.,1966;Bieniawski,1967;Eberhardt et al.,1997; Martin,1997).Furthermore,unlike other materials(e.g.metals), rocks exhibit a strongly pressure-dependent mechanical behavior (Jaeger and Cook,1976).A variation of failure mode,from axial splitting to shear band formation,is indeed often observed for increasing conf i ning pressures(Horii and Nemat-Nasser,1986). This variation of failure behavior is ref l ected in a non-linear failure envelope(Kaiser and Kim,2008)and a transition from brittle to ductile post-peak response(Paterson and Wong,2004).At rock mass level,the failure process observed during laboratory-scale experiments is further complicated by the presence of discontinuities,such as joints,faults,shear zones,schistosity planes,and bedding planes(Goodman,1989).Speci fi cally,discontinuities affect the response of the intact rock by reducing its strength and inducingnon-linearitiesandanisotropyinthestress-strain response(Hoek,1983;Hoek et al.,2002).Furthermore,discontinuities add kinematic constraints on the deformation and failure modes of structures in rocks(Hoek et al.,1995;Hoek,2006)and cause stress and displacement redistributions to sensibly deviate from linear elastic,homogenous conditions(Hammah et al.,2007).

Aside from the intrinsic uncertainties associated with the determination of reliablein situinput parameters,the application of numerical modeling tothe analysis of rock engineering problems represents a challenging task owing to the aforementioned features of the rock behavior.In particular,the progressive degradation of material integrity during the deformation process,together with the in fl uence of pre-existing discontinuities on the rock mass response,has represented a major drive for the development of new modeling techniques.In this context,the available numerical approachesaretypicallyclassi fi edeitherascontinuum-or discontinuum-based methods(Jing and Hudson,2002).

The main assumption of continuum-based methods is that the computational domain is treated as a single continuous body. Standard continuum mechanics formulations are based on theories such as plasticity and damage mechanics,which adopt internal variables to capture the in fl uence of history on the evolution of stress and changes at the micro-structural level,respectively(De Borst et al.,2012).Conventionally,the implementation of continuum techniques is based on numerical methods,such as non-linear fi nite element method(FEM),Lagrangian fi nite difference method(FDM),and boundary element method(BEM),with the incorporationofplasticity-basedmaterialmodels.However,standard strength-based strain-softening constitutive relationships cannot capture localization of failure as the lack of an internal length scale results in the underlying mathematical problem to become illposed(De Borst et al.,1993).Among the main consequences of adopting a standard continuum tosimulate strain localization is the fact that,by doing so,localization occurs in a region of zero thickness and consequently an unphysical mesh sensitivity arises.To overcome these shortcomings,the description of the continuum must account either for the viscosity of the material,by incorporating a deformation-rate dependency,or for the change in the material micro-structure,by enhancing the mathematical formulation with additional terms(De Borst et al.,1993).The latter technique,known as regularization,includes non-local(e.g.Baˇzant and Pijaudier-Cabot,1988),gradient(e.g.Mühlhaus and Aifantis, 1991),and Cosserat micro-polar(e.g.Mühlhaus and Vardoulakis, 1987)models.Alternatively,cohesive-crack models have been proposed under the assumption that damage can be represented by a dominant macro-fracture lumping all non-linearities into a discrete line(e.g.Hillerborg et al.,1976;Baˇzant and Oh,1983).That is,a f i ctitious crack concept is employed to represent the effect of a fracture process zone(FPZ)ahead of the crack tip,whereby phenomena such as small-scale yielding,micro-cracking or void growth and coalescence are assumed to take place.For the case of heterogeneous rocks,strain localization has also been successfully simulated by damage models with statistically distributed defects. A number of variations of this approach have been developed for numerical schemes such as FEM(Tang,1997),FDM(Fang and Harrison,2002),smooth-particle hydrodynamics(SPH)(Ma et al., 2011),cellular automaton(Feng et al.,2006),and lattice models (Blair and Cook,1998).

Within continuum models,two approaches are commonly employed to account for the presence of rock mass discontinuities. If the number of discontinuities is relatively large,homogenization techniques are typically adopted.The most widely used homogenization approach consists of reducing,within a conventional elasto-plastic model,the rock mass deformation modulus and strength parameters to account for the degrading effect induced by the local geological conditions(Hoek et al.,2002;Hoek and Diederichs,2006).More advanced models can also include transversely isotropic elastic response induced by preferably oriented joints(Amadei,1996)orfailure-inducedplasticanisotropic behavior(e.g.Mühlhaus,1993;Dyszlewicz,2004).However,the classic homogenization approach is typically limited by the fact that slip,rotations and separation as well as size effects induced by discontinuities cannot be explicitly captured(Hammah et al., 2008).Alternatively,if the problem is controlled by a relatively low number of discrete features,special interface(or joint)elements can be incorporated into the continuum formulation(e.g. Goodman et al.,1968;Ghaboussi et al.,1973;Wilson,1977;Pande and Sharma,1979;Bfer,1985).This technique,also known as the combined continuum-interface method(Riahi et al.,2010),can accommodate large displacements,strains and rotations of discrete bodies.However,it is accurate as long as changes in edge-to-edge contacts along the interface elements are negligible throughout the solution(Hammah et al.,2007).That is,owing to the f i xed interconnectivity between solid and joints and the lack of an automatic scheme to recognize new contacts,only small displacement/rotations along joints can be correctly captured(Cundall and Hart,1992).

Discrete(or discontinuous)modeling techniques,commonly referred to as the discrete element method(DEM),treat the material directly as an assembly of separate blocks or particles.According to the original def i nition proposed by Cundall and Hart (1992),a DEM is any modeling technique that(i)allows f i nite displacements and rotations of discrete bodies,including complete detachment;and(ii)recognizes new contacts automatically as the simulation progresses.DEMs were originally developed to eff iciently treat solids characterized by pre-existing discontinuities having spacing comparable to the scale of interest of the problem under analysis and for which the continuum approach described above may not provide the most appropriate computational framework.These problems include:blocky rock masses,ice plates, masonry structures,and f l ow of granular materials.DEMs can be further classif i ed according to several criteria regarding,for instance,the type of contact between bodies,the representation of deformability of solid bodies,the methodology for detection and revision of contacts,and the solutionprocedure for the equations of motion(Jing and Stephansson,2007).Based on the adopted solution algorithm,DEM implementations are broadly divided into explicit and implicit methods.The termdistinct element methodrefers to a particular class of DEMs that use an explicit time-domain integration scheme to solve the equations of motion for rigid or deformable discrete bodies with deformable contacts(Cundall and Strack,1979a).The most notable implementations of this group are arguably represented by the universal distinct element code (UDEC)(Itasca Consulting Group Inc.,2013)and the particle f l ow code(PFC)(Itasca Consulting Group Inc.,2012b).On the other hand, the best known implicit DEM is the discontinuous deformation analysis(DDA)method(Shi and Goodman,1988).Despite the fact that DEMs were originally developed to model jointed structures andgranularmaterials,theirapplicationwassubsequently extended to the case of systems where the mechanical behavior is controlled by discontinuities that emerge as natural outcome of the deformation process,such as fracturing of brittle materials.Specif i cally,the introduction of bonding between discrete elements allowed capturing the formation of new fractures and,thus, extended the application of DEMs to simulate also the transition from continuum to discontinuum.

As observed by Biˊcaniˊc(2003),the original boundary between continuum and discontinuum techniques has become less clear as severalcontinuumtechniquesarecapableofdealingwithemergent discontinuities associated with the brittle fracture process.In particular,the hybrid approach known as the combined f i nitediscrete element method(FDEM)(Munjiza et al.,1995;Munjiza, 2004)effectively starts from a continuum representation of the domainbyf i niteelementsandallowsaprogressivetransitionfroma continuumtoa discontinuumwith insertion of new discontinuities.

The goal of this reviewpaper is toprovide a summaryof selected discrete element and hybrid f i nite-discrete element modeling techniques that have recently emerged in the f i eld of rock mechanics as simulation tools for fracturing processes in rocks and rock masses.Specif i cally,the commercially available codes PFC (Itasca Consulting Group Inc.,2012b),UDEC(Itasca Consulting Group Inc.,2013)and ELFEN(Rockf i eld Software Ltd.,2004)as well as the open-source software Yade(Kozicki and Donzé,2008) and Y-Geo(Mahabadi et al.,2012a)are considered.Also,extensions of the DDA method to simulate fracturing processes are described. For each code,the fundamental implementation principles are illustrated with particular emphasis on the approach specif i cally adopted to simulate fracture nucleation and propagation and to account for the presence of rock mass discontinuities.The description of the governing principles is accompanied by a brief review of application studies focusing on laboratory-scale models of rock failure processes and on the simulation of damage development around underground excavations.For more extensive reviews of numerical methods in rock mechanics,the reader can refer to the work of Jing and Hudson(2002)and Jing(2003),with a detailed illustration of fundamentals and applications of DEMsprovided by Jing and Stephansson(2007)and Bobet et al.(2009). Also,a review of modeling techniques for the progressive mechanical breakdown of heterogeneous rocks and associated fl uid fl ow can be found in Yuan and Harrison(2006).

2.Discrete element methods

2.1.Particle-based models:the PFC and Yade

2.1.1.Fundamental principles

Particle-based models were originally developed to simulate the micromechanical behavior of non-cohesive media,such as soils and sands(Cundall and Strack,1979a).With this approach,the granular micro-structure of the material is modeled as a statistically generated assembly of rigid circular particles of varying diameters. The contacts between particles are typically assigned normal and shear stiffnesses as well as a friction coeff i cient.The commercially available code PFC represents an evolution of previous particlebased codes,namely BALL and TRUBAL(Cundall and Strack, 1979b),which applies cohesive bonds between particles to simulate the behaviors of solid rocks.The resultant model is commonly referred to as the bonded-particle model(BPM)for rock(Potyondy and Cundall,2004).In a BPM,crack nucleation is simulated through breaking of internal bonds while fracture propagation is obtained by coalescence of multiple bond breakages.Blocks of arbitrary shapes can form as a result of the simulated fracturing process and can subsequently interact with each other.

Two types of bonds are typically used in PFC:the contact bond and the parallel bond.In the contact bond model,an elastic spring with constant normal and shear stiffnesses,knandks,acts at the contact points between particles,thus allowing only forces to be transmitted.In the parallel bond model,the moment induced by particle rotation is resisted by a set of elastic springs uniformly distributed over a f i nite-sized section lying on the contact plane and centered at the contact point(Fig.1).This bond model reproduces the physical behavior of a cement-like substance gluing adjacent particles together.

As further described in the next section,parallel bond rock models have been widely used to study fracturing and fragmentation processes in brittle rocks.However,one of the major drawbacks of this type of model is the unrealistically low ratios of the simulated unconf i ned compressive strength to the indirect tensile strength for synthetic rock specimens(Cho et al.,2007;Kazerani and Zhao,2010);the straightforward adoption of circular(or spherical)particles cannot fully capture the behavior of complexshaped and highly interlocked grain structures that are typical of hard rocks.Furthermore,low emergent friction values are simulated in response to the application of conf i ning pressure.To overcome these limitations,a number of enhancements to PFC were proposed.Potyondy and Cundall(2004)showed that by clustering particles together(Fig.2a)more realistic macroscopic friction values can be obtained.Specif i cally,the intra-cluster bond strength is assigned a different strength value than the bond strength at the cluster boundary.Cho et al.(2007)showed that by applying a clumped-particle geometry(Fig.2b)a signif i cant reduction of the aforementioned def i ciencies can be obtained, thereby allowing one to reproduce correct strength ratios,nonlinear behavior of strength envelopes and friction coeff i cients comparable with laboratory values.More recently,Potyondy(2012) developed a new contact formulation,namely the f l at-joint model, aimed at capturing the same effects of a clumped BPM(or of a grain-based UDEC model as described below)with a computationally more eff i cient method(Fig.2c).The partial interface damage and continued moment-resisting ability of the f l at-joint model allow the user to correctly match both the direct tensile and the unconf i ned compressive strengths of a hard rock.

Another issue arising from the particle-based material representation of PFC is the inherent roughness of interface surfaces representing rock discontinuities(Fig.3a).This roughness typically results in an artif i cial additional strength along frictional or bonded rock joints.This shortcoming was overcome by the development of the smooth-joint contact model(SJM)(Mas Ivars et al.,2008), which allows one to simulate a smooth interface regardless of the local particle topology(Fig.3b).The combination of the BPM to capture the behavior of intact material with the SJM for joint network leads to the development of the so-calledsynthetic rock mass(Mas Ivars et al.,2011),which aims at numerically predicting rock mass properties,including scale effects,anisotropy and brittleness,that cannot be obtained using empirical methods.

Fig.1.The parallel bond model implemented in PFC.(a)Normal and shear stiffnesses between particles.The contact stiffnesses,knandks,remain active even after the bond breaks as long as particles stay in contact.The bond stiffnesses(per unit area),,are suddenly removed when the bond breaks regardless of whether particles stay in contact or not. (b)Constitutive behavior in shear and tension(i=s,n).Figures redrawn after Potyondy and Cundall(2004)and Cho et al.(2007).

The particle-based code Yade(Kozicki and Donzé,2008,2009; ˇSmilauer et al.,2010)has been recently introduced as an alternative modeling platform to the commercial software PFC described above.The major aims of the Yade project are(i)to provide enhanced f l exibility in terms of adding new modeling capabilitiesand(ii)to promote code improvement through open-source development and direct feedback from the scientif i c community. In its basic formulation,the contact laws implemented in Yade share the same principles of those available in PFC.Small deformations are captured bylinearelastic interaction forces between contacting discs/spheres.Rock fracturing is captured by the rupture of bonds,whose strength is characterized by a constant maximum acceptable force in tension and a cohesive-frictional maximum acceptable force in shear.Similar to PFC,the shear strength drops instantaneously to a purely frictional resistance after failure. Conversely,in tension,after the maximum force is reached,the stiffness can be varied by a softening factor,ζ,controlling the energy released due to bond breakage(Fig.4a).Rock discontinuities can be treated in Yade using a contact logic analogous to the SJM of PFC(Scholtès and Donzé,2012)(Fig.3b).Specif i cally,the interactions between bonds crossing a prescribed discontinuity plane are identif i ed and then re-oriented according to the joint surface, thus ensuring a frictional behavior that is independent of the inherent roughness induced by the particle topology.Furthermore, similar to the aforementioned SRM approach,sets of pre-existing discontinuities can be explicitly introduced in a Yade model as three-dimensional(3D)discrete fracture networks(Scholtès and Donzé,2012).Applications of Yade to the investigation of the fundamentals of brittle rock failure have led to the implementation of an interaction range coeff i cient,γ,which can be used to link particles not directly in contact one with the other,yet located in the neighboring region(Scholtès and Donzé,2013)(Fig.4b).By doing so,the degree of interlocking between particles can be effectively controlled,thus allowing one to accurately model high ratios of compressive to tensile strengths as well as non-linear failure envelopes.This approach represents an alternative to the clumping logic and the f l at-joint contact model of PFC.

Main advantages of the particle-based modeling methodology include the simple mathematical treatment of the problem, whereby complex constitutive relationships are replaced by simple particle contact logic,and the natural predisposition of the approach to account for material heterogeneity.On the other hand, considering the high level of simplif i cation introduced,extensive experimental validation is needed to verify that the method can capture the observed macroscopic behavior of rock.Moreover,an extensive calibration based on experimentally measured macroscale properties is required to determine the contact parameters that will predict the observed macro-scale response.

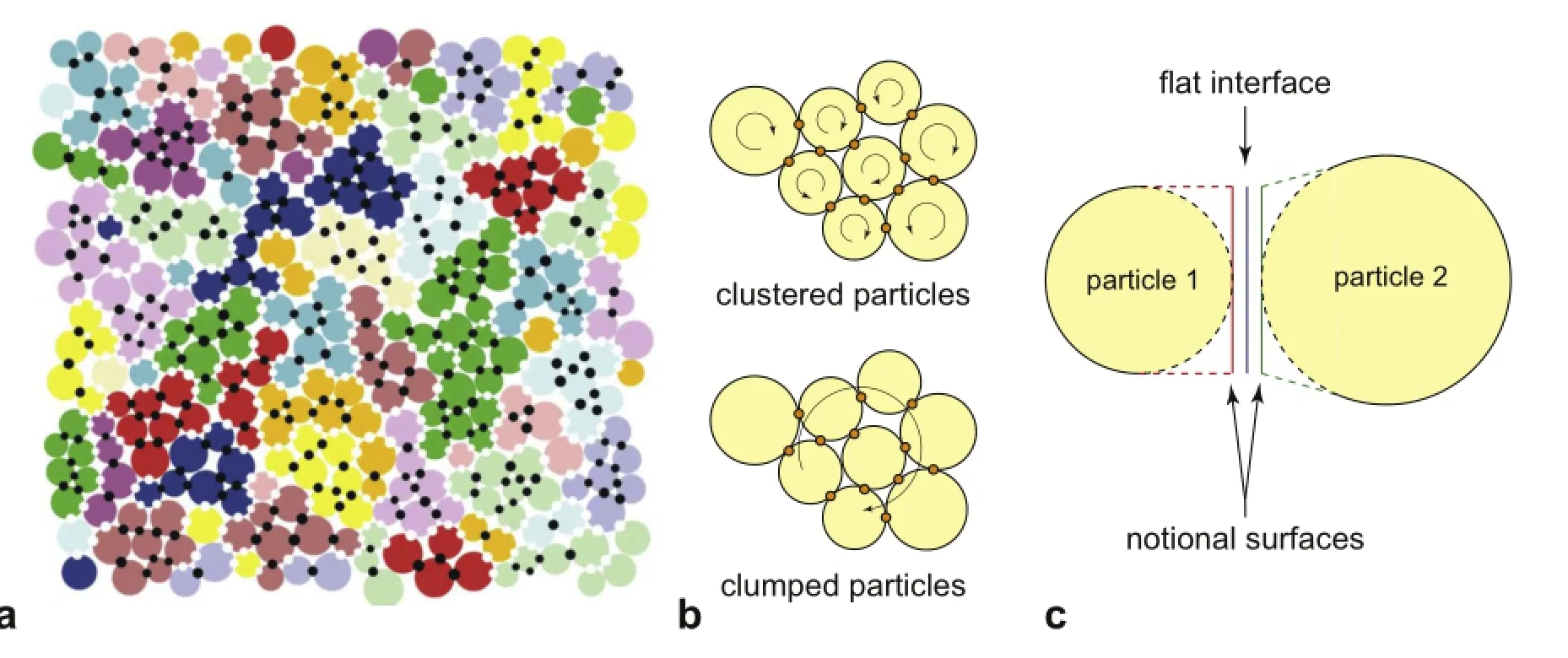
Fig.2.Proposed enhancements to the original BPM to capture realistic values of the ratio of unconf i ned compressive strength to indirect tensile strength.(a)Particle clustering (after Potyondy and Cundall(2004)),(b)clustered particles vs.clumped particles(after Cho et al.(2007),redrawn),and(c)f l at-joint contact model showing the effective interface geometry(after Potyondy(2012),redrawn).

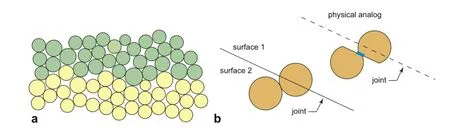
Fig.3.Representation of rock joints in PFC.(a)Traditional representation with rough surface,and(b)smooth-joint contact model.Figures redrawn after Mas Ivars et al.(2011).

2.1.2.Applications

PFC has been extensively used within the rock mechanics community to numerically investigate the fundamental processes of brittle fracturing in rocks by means of laboratory-scale models. Potyondy et al.(1996)f i rst proposed a synthetic PFC model that could reproduce modulus,unconf i ned compressive stress,and crack initiation stress of the Lac du Bonnet Granite.Extended results were illustrated by Potyondy and Cundall(2004)with the simulation of the stress-strain behavior during biaxial compression tests for varying conf i ning pressures.Several features of the rock behavior emerged from the BPM,including elasticity,fracturing,damageaccumulationproducingmaterialanisotropy,dilation,post-peak softening and strength increase with conf i nement.Since PFC simulates quasi-static deformation by solving the equations of motion,elasto-dynamics effects,such as stress wave propagation and cracking-induced AE,can be explicitly simulated. In this context,Hazzard and Young(2000)developed a technique to dynamically quantify AE in a PFC model.The approach was validated by simulating the seismicbvalue of a conf i ned test on granite.The aforementioned approach was further improved by introducing moment tensor calculation based on change in contact forces uponparticle contact breakage and was applied tothe microseismic simulation of a mine-by experiment in a crystalline rock (Hazzard and Young,2002)and of an excavation-induced fault slip event(Hazzard et al.,2002).3D simulations of acoustic activity using PFC3D were proposed by Hazzard and Young(2004). Diederichs(2003)used PFC simulations to explore the aspects of grain-scale tensile damage accumulation under both macroscopically tensile and compressive conditions.A BPM was employed as numerical analog to study the effects of tensile damage and the sensitivity tolowconf i nement in controlling the failureof hardrock masses in proximity of underground excavations.Application of PFC to determining the fracture toughness of synthetic rock-like specimen was illustrated by Moon et al.(2007).Analyses of failure and deformation mechanisms during direct shear loading of rock joints have also been carried out toobtain original insights into rock fracture shear behavior and asperity degradation.Rasouli and Harrison(2010)investigated the relation between Riemannian roughness parameter and shear strength of prof i les comprising symmetric triangular asperities sheared at different normal stress levels.Asadi et al.(2012)extended the previous results with consideration of the shear strength and asperity degradation processes of several synthetic prof i les including triangular,sinusoidal and randomly generated prof i les.Zhao(2013)simulated singleand multi-gouge particles in a rough fracture segment undergoing shear and analyzed the behavior of gouge particles as function of the applied conf i nement.Another important mechanism of the failure process in rocks,such as the initiation and propagation of cracks from pre-existing f l aws,has been analyzed using BPM. Zhang and Wong(2012)numerically simulated the cracking process in rock-like material containing a single f l aw under uniaxial compression,while Zhang and Wong(2013)investigated the coalescence behavior for the case of two stepped and coplanar preexisting open f l aws.The effect of conf i nement on wing crack propagation was studied by Manouchehrian and Marji(2012).

Fig.4.The particle-based code Yade.(a)Interaction law between particle in tension and compression,and(b)effect of the interaction range coeff i cient,γ,on the simulated contact fabric.Figures redrawn after Scholtès and Donzé(2013).

Fig.5.Simulation of fracture development around underground excavation using PFC.(a)Modeling of notch formation around the AECL’s mine-by experiment tunnel(after Potyondy and Cundall(2004)).(b)Damaged notches around a hole under biaxial compression(after Fakhimi et al.(2002)).

BPMs have been successfully applied to the study of damaged zones around underground openings.The spalling phenomena observed around the Atomic Energy of Canada Limited’s(AECL) mine-by experiment tunnel(Martin et al.,1997)were f i rst simulated by Potyondy and Cundall(1998).Further analysis of the notchformation process in terms of coalescence of ruptured bonds was provided by Potyondy and Cundall(2004)using a PFC2D model embedded in a continuum f i nite-difference model(Fig.5a). Hazzard and Young(2002)provided a micro-seismic simulation of the same excavation by comparing the actual seismicity recorded underground with the simulated spatial and temporal distribution of events.The effect of low stiffness spray-on liner of fracture propagation based onin situconditions of the above mentioned mine-by experiment was numerically studied by Tannant and Wang(2004).Similarly,Potyondy and Cundall(2000)used PFC2D to predict damage formation adjacent to a circular excavation in an anisotropic gneissic tonalite at the Olkiluoto deep geological repository.Fakhimi et al.(2002)showed that a BPM could match failure load,crack pattern,and spalling observed during a biaxial compression test on a sandstone specimen with a circular opening (Fig.5b).Numerical studies on thermally-induced fracturing around openings in granite were carried out by Wanne and Young (2008)and Wanne(2009)for a laboratory-scale heater experiment and the AECL’s Tunnel Sealing Experiment,respectively.Sagong et al.(2011)investigated the inf l uence of the joint angle on the rock fracture and joint sliding behaviors around an opening in a jointed rock model.

Simulation studies using the open-source code Yade have been focused to date on the role played by discrete fracture networks (DFNs)(Scholtès et al.,2011;Harthong et al.,2012;Scholtès and Donzé,2012)and grain interlocking(Scholtès and Donzé,2013) in controlling the mechanical responses of 3D rock samples.

2.2.The universal distinct element code(UDEC)

2.2.1.Fundamental principles

In UDEC the computational domain is discretized into blocks using a f i nite number of intersecting discontinuities.Each block is internally subdivided using a f i nite difference,or a f i nite volume, scheme for calculation of stress,strain and displacement.Model deformability is captured by an explicit,large strain Lagrangian formulation similar to the continuum code FLAC(Itasca Consulting Group Inc.,2012a).The mechanical interaction between blocks is characterized bycompliant contacts using a f i nite stiffness together with a tensile strength criterion in the normal direction,and a tangential stiffness together with a shear strength criterion(e.g. Coulomb-type friction)in the tangential direction to the discontinuity surface.Similar to PFC,static problems are treated using a dynamic relaxation technique by introducing viscous damping to achieve steady state solutions.

When using the classic formulation of UDEC,rock failure is captured either in terms of plastic yielding(e.g.Mohr-Coulomb criterion with tension cut-off)of the rock matrix or displacements (i.e.sliding,opening)of the pre-existing discontinuities.That is, new discontinuities cannot be drivenwithin the continuum portion of the model and therefore discrete fracturing through intact rock cannot be simulated.However,Lorig and Cundall(1989)showed that this shortcoming can be overcome by introducing a polygonal block pattern,such as the Voronoi tessellation,to the UDEC capability.As depicted in Fig.6,a physical discontinuity is created when the stress level at the interface between block exceeds a threshold value either in tension or in shear.Although new fractures are so propagated,this technique is not based on a linear elastic fracture mechanics(LEFM)approach.That is,unlike classic LEFM models, fracture toughness and stress intensity factors are not considered. Furthermore,material softening in the FPZ,typicallycaptured using cohesive-crack models,is disregarded.

Although polygonal block models are computationally more expensive than particle-based ones,they can provide a more realistic representation of the rock micro-structure(Lemos,2012). Owing to the full contact between grains and better interlocking offered by the random polygonal shapes,the grain-based UDEC model overcomes some of the limitations of parallel-bonded particle models,as further described below.

2.2.2.Applications

Owing to the above mentioned characteristics,grain-based DEMs have been employed to study the fracturing behavior of rocks.Christianson et al.(2006)used a grain-based UDEC model to numerically complement laboratory testing on a lithophysal rock underconf i nedconditions.Themechanicaldegradationof thesame rock type was investigated by Damjanac et al.(2007)using a similar technique.The model was then upscaled to study the stability of emplacement drifts at Yucca Mountain under mechanical,thermal, and seismic loading as well as time-dependent effects.Using a UDEC-Voronoi model,Yan(2008)investigated the laboratory-scale step-path failure(e.g.wing cracking and fracture coalescence)in a sample containing pre-existing joints with application to slope stability problems.A similar approach was adopted by Lan et al. (2010)to numerically assess the effect of heterogeneity on the micromechanical extensile behaviorduring compressive loadingon Lac du Bonnet Granite and Äspö Diorite.The model directly incorporated several sources of heterogeneity,including microgeometric heterogeneity,grain-scale elastic heterogeneity,and microcontact heterogeneity.A calibration procedure to determine a unique set ofmicro-parameters for a grain-based UDEC model was developed by Kazerani and Zhao(2010)(Fig.7a).A series of numerical experiments(i.e.uniaxial/biaxialcompressionandBraziliantension)were used to assess the relationship between macro-and microparameters.The model was also shown to correctly capture the ratio of compressive to tensile strengths of rock samples measured in the laboratory,therefore overcoming some of the original defects of parallel-bonded particle models.Finally,the grain-based UDEC approach was also employed to study the effect of joint persistence on the evolution of damage during direct shear tests(Alzo’ubi, 2012).

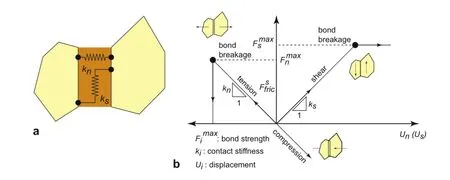
Fig.6.UDEC modeling of fracture propagation in rock.(a)Normal and shear stiffnesses between blocks.(b)Constitutive behavior in shear and tension(i=s,n).Figures redrawn after Kazerani and Zhao(2010).

Last,it is worth mentioning three approaches that were proposed to capture fracture processes in UDEC as an alternative to the adoption of a polygonal structure.Firstly,based on fracture mechanics considerations,a time-dependent joint cohesion was implemented by Kemeny(2005)to capture the progressive mechanical degradation during the failure of rock bridges along discontinuities.The model was validated using several laboratoryscale examples and then was used to investigate the timedependent degradation of drifts for the storage of nuclear waste at Yucca Mountain.Secondly,Jiang et al.(2009)developed an expanded distinct element method(EDEM)based on UDEC whereby potential cracks,with bonding strengths equivalent to the rock matrix,are pre-distributed within the model based on the plastic regions and direction of principal stresses obtained from a preliminaryelasto-plastic analysis.The approach was applied tothe simulation of cracking around a large underground excavation in a blocky rock mass.Lastly,Kazerani et al.(2012)implemented a UDEC model which represents the rock material as a collection of irregular-sized deformable triangles with cohesive boundaries controlling the material fracture and fragmentation properties (Fig.7b).A reasonable agreement was found between numerical simulation and experimental laboratory results of compressive, tensile and shear tests on plaster(Kazerani,2013).As further illustrated in Section 3.2,this model shares several characteristics of the Y-Geo implementation of the combined FDEM.

2.3.The discontinuous deformation analysis(DDA)method

The DDA method is an implicit DEM originally proposed by Shi and Goodman(1988)to simulate the dynamics,kinematics,and elastic deformability of a system contacting rock blocks.Similar to classic f i nite element formulations,the governing equations are represented by a global system of linear equations which are obtained by minimizing the total potential energy of the system. Displacements and strains are taken as variables and the stiffness matrix of the model is assembled by differentiating several energy contributions including block strain energies,contacts between blocks,displacement constraints and external loads.An implicit formulation is used to solve the system of equations.In the basic DDA implementation,each block is simply deformable as the strain and stress f i elds are constant over the entire block area.However, improved deformability models can be achieved by introducing higher order strain f i elds or by subdividing each block into a set of simply deformable sub-blocks(Lin et al.,1996).The imposition of contact constraints between blocks can be obtained by a number of methods including the penalty method,the Lagrange multiplier method or the augmented Lagrangian method.The frictional behavior along block interfaces is modeled by a Mohr-Coulomb criterion.

Traditionally,DDA simulations have been employed to capture failure along predef i ned structural planes in blocky rock masses (e.g.Hatzor and Benary,1998;Bakun-Mazor et al.,2009;Hatzor et al.,2010).Nevertheless,some attempts have been made to introduce fracturing capabilities within the DDA framework.The simplest technique is similar to the UDEC-Voronoi approach:fracturing is captured as debonding of artif i cial block interfaces if a Mohr-Coulomb with tension cut-off criterion is locally violated (Ke,1997).A second approach involves comparing the maximum and minimum principal stresses calculated at each block centroid with a three-parameter Mohr-Coulomb criterion.If the criterion is satisf i ed,appropriate fracture plane directions are computed(i.e. one axial splitting plane in tension or two conjugated planes in shear)and the block is then subdivided into multiple sub-blocks. Simple validation of this method was presented by Koo and Chern(1997)using uniaxial and conf i ned compression as well as uniaxial tension test models.Finally,Lin et al.(1996)proposed an algorithm based on an iterative sub-block approach which allows one to capture continuous crack growth from the tip of a preexisting f l aw.

Recently,a new method,known as the discontinuous deformation and displacement(DDD)method,has been developed by Tang and Lü(2013)by merging DDA with a continuum-based damage mechanics code,namely the rock failure process analysis (RFPA)program(Tang,1997).The model aims at combining the advantages of DDA to capture the large-displacement mechanics ofdiscontinuous systems with the capabilities of RFPA to simulate the small-strain deformational mechanisms characterizing the failure process of intact rock material.

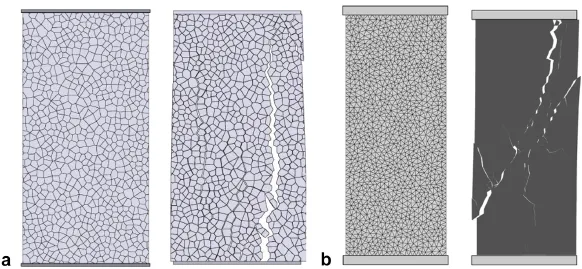
Fig.7.Simulations of rock failure under compression using UDEC.(a)Uniaxial compression test on Augite granite using a grain-based model(after Kazerani and Zhao(2010)).(b) Uniaxial compression test on plaster using a cohesive boundary approach(after Kazerani et al.(2012)).

Fig.8.Nodal fracture scheme of ELFEN.(a)Initial state before fracturing,(b)intra-element crack insertion,and(c)inter-element crack insertion.Figure redrawn after Klerck(2000).

3.The hybrid f i nite-discrete element method(FDEM)

In the hybrid continuum-discontinuum technique known as the combined FDEM,the simulation starts with a continuous representation of the solid domain of interest.As the simulation progresses, typicallythroughexplicitintegrationoftheequationsofmotion,new discontinuities are allowed to form upon satisfying some fracture criterion,thus leading to the formation of new discrete bodies.In general,the approach blends FEM techniques with DEM concepts (Barla and Beer,2012).The latter algorithms include techniques for detecting new contacts and for dealing with the interaction between discrete bodies,while the former techniques are used for the computation of internal forces and for the evaluation of a failure criterion and the creation of new cracks.Hybrid f i nite-discrete element models should not be confused with coupled continuumdiscontinuum approaches(e.g.Pan and Reed,1991;Billaux et al., 2004)which represent the problem of far-and near-f i elds using continuum-based and DEM techniques,respectively.

Fig.9.Simulation of borehole breakout in different rock types using ELFEN;left:brittle failure,right:ductile failure(after Klerck(2000)).

Fig.10.ELFEN simulation of rock failure under compression.(a)Evolution of fracturing during the simulation of a conf i ned compression test on sandstone(after Klerck et al. (2004)).(b)Final fracture patterns for triaxial compression test simulations for increasing values of the intermediate principal stress,σ2(after Cai(2008)).

In the following sections,the fundamental principles of two common FDEM implementations are brief l y illustrated,namely ELFEN(Rockf i eld Software Ltd.,2004)and Y-Geo(Munjiza,2004; Mahabadi,2012),as well as their applications to the study of the fracturing behavior of rocks.

3.1.ELFEN

3.1.1.Fundamental principles

The continuum formulation of ELFEN is based on the explicit fi nite element method.Material softening(or hardening)is captured using a non-associative Mohr-Coulomb elasto-plastic model with shear strength parameters,including cohesion,friction angle and dilation,de fi ned as function of the effective plastic strain.The localization of strain is obtained by regularizing the standard description of the continuum with the incorporation of fracture mechanics principles in the equations governing the evolution of state variables(Owen and Feng,2001;Klerck et al.,2004). In particular,material softening associated with fracturing is captured under the main assumption that the quasi-brittle failure is extensional in nature.As thoroughly described by Klerck(2000), the extensional failure is modeled directly and indirectly for the cases of tensile stress and compressive stress f i elds,respectively. Under direct tension,several constitutive models can be used such as the rotating crack and the Rankine tensile smeared crack.With these models,material strain softening is fully governed by the tensile strength and the specif i c fracture energy parameters.Under compressive stress f i elds,a Mohr-Coulomb yield criterion is combined with a fully anisotropic tensile smeared crack model. With this approach,known as thecompressive fracture model,the extensional inelastic strain associated with the dilation response is explicitlycoupled with the tensile strength in the dilation direction. That is,increments of extensional strain are associated with tensile strength degradation in the perpendicular direction.

Upon localization of damage into crack bands and complete dissipation of the fracture energy,a discrete fracture is realized. Hence,the transition from continuous to discontinuous behavior involves transferring a virtual smeared crack into a physical discontinuity in the f i nite element mesh(Owen and Feng,2001). The mesh topology update is based on a nodal fracture schemewith all new fractures developing in tension(i.e.Mode I)in the direction orthogonal to the principal stress direction where the tensile strength becomes zero.This procedure is numerically accomplished by f i rst creating a non-local failure map for the whole domain based on the weighted nodal averages of a failure factor, def i ned as the ratio of the inelastic fracturing strain to the critical fracturing strain.Secondly,a failure direction is determined for each nodal point where the failure factor is greater than one based on the weighted average of the maximum failure strain directions of all elements connected to the node.Finally,a discrete crack is inserted through the failure plane.As depicted in Fig.8,the insertion of a new crack can be accomplished using two differentalgorithms(Klerck et al.,2004).Theintra-elementinsertion drives a new fracture along the crack propagation direction by directly splitting the f i nite elements.In this case,a local adaptive remeshing may be necessary to achieve an acceptable element topology and avoid highly-skewed sliver elements that could decrease the numerical stability threshold of the integration time step.Conversely,with theinter-elementinsertion,the discrete crack is snapped to the existing element edge most favorably oriented with respect to the failure plane.Following the crack insertion,the damage variables in the adjacent f i nite elements are set to zero and the contact along the two newly-created surfaces is treated using a contact interaction algorithm(e.g.penalty or Lagrangian multiplier method).

Fig.11.Simulation of fracture propagation with Y-Geo.(a)Representation of a continuum using cohesive elements interspersed throughout a mesh of triangular elements.(b) Constitutive behavior of the crack elements def i ned in terms of bonding stress(tensile,σ,and shear,τ)vs.relative displacement(opening,o,and sliding,s)between the edges of adjacent triangular elements.

3.1.2.Applications

First applications of ELFEN to modeling rock failure under compressive loads were proposed by Klerck(2000).In particular, the simulation of borehole breakouts indicated that the aforementioned compressive fracture model of ELFEN can describe both the axial splitting typical of brittle materials and the shear failure usually observed in more ductile ones(Fig.9).A study of fracture development around deep tunnels was proposed by Sellers and Klerck(2000)using laboratory-scale models.As observed in the laboratory,the model could reproduce fractures developing subparallel to the excavation boundary as well as the conf i ning effect of pre-existing joints on the development of damage.Moreover,the experimentally measured acoustic activity was analyzed using the release of kinetic energy simulated by the model as numerical equivalent.Coggan et al.(2003)described several examples of rock engineering application of ELFEN,including stability analysis of roof beams and pillars in underground excavations and rock slope stability problems.Klerck et al.(2004)proposed a quantitative analysis of compression tests on rocks with direct comparison of the load-displacement response and of the evolution of fracture development with experimental data(Fig.10a).This type of analysis was subsequently extended to 3D models that aimed at studying the inf l uence of the intermediate principal stress on rock fracturing and strength near excavation boundaries(Cai,2008).The results clearlyshowed that the generation of tunnel surface parallel fractures and microcracks can be attributed to material heterogeneity and to the existence of relatively high intermediate principal stress as well as zero to low minimum principal stress conf i nement (Fig.10b).Investigations of failure behavior of rock specimens under indirect tensile stress conditions were f i rst proposed by Cai and Kaiser(2004)and,more recently,by Cai(2013).The simulation of crack initiation and propagation from a pre-existing f l aw highlighted the inf l uence of the f l aw frictional resistance on the development of primary and secondary cracks as well as on the failure load.Application of ELFEN to the investigation of damage mechanisms(e.g.surface wear and tensile fracturing)along joint planes under direct shear conditions was illustrated by Karami and Stead(2008).A discrete fracture rock mass model was proposed by Pine et al.(2006)by combining an ELFEN model with the fracture geometry generated by a DFN software.The approach was used to obtain insights into the inf l uence of pre-existing joints on the rock mass behavior in underground pillars,rock slides,and block caving operations(Eberhardtet al.,2004;Pine et al.,2007;Elmo and Stead, 2010;Vyazmenskyet al.,2010a,b).Yan(2008)numericallyanalyzed fracture coalescence and rock failure mechanisms in laboratoryscale specimens containing step-path fractures.The study was also extended to the simulation of rock bridge fracture associated with potential toe breakout failure in large open pit slopes.Original application of ELFEN to the investigation of failure behavior of layered rocks can be found in Stefanizzi(2007)and Stefanizzi et al. (2008).

3.2.Y-Geo

3.2.1.Fundamental principles

The continuum representation of Y-Geo is based on the discretization of the modeling domain with three-noded triangular elements together with four-noded cohesive elements embedded between the edges of all adjacent triangle pairs(Fig.11a).The elastic deformation of the bulk material is captured by the constant-strain,linear-elastic triangular elements with impenetrability between elements enforced by a penalty function method (Munjiza and Andrews,2000).Fracture nucleation within the continuum is simulated by the breakage of the cohesive elements (Munjiza et al.,1999).Since fractures can nucleate only along the boundaries of the triangular elements,arbitrary fracture trajectories can be reproduced within the constraints imposed by the initial mesh topology.Unlike ELFEN,the mesh topology in Y-Geo is never updated during the simulation and re-meshing is not performed.Consequently,a suff i ciently small element size should be adopted to reproduce the correct mechanical response(Munjiza and John,2002).

Fig.12.Simulation of rock fracture under compression using Y-Geo.(a)Final fracture patterns of a biaxial compression test simulation on a heterogeneous rock sample at increasing conf i ning pressures,σ3(after Mahabadi et al.(2012b)).(b)Final fracture patterns of a unconf i ned compression test simulation on layered rock samples(after Lisjak et al.(2014a)).

The constitutive behavior of crack elements is implemented in terms of relative displacement between opposite triangle edges and incorporates principles of non-linearelastic fracture mechanics (Fig.11b).Material starts toyield,in tension or shear,upon reaching a displacement value corresponding tothe peak cohesive strengths. The Mode I peak strength is def i ned by a constant tensile strength,ft,while the Mode II peak strength,fs,is computed according to the Mohr-Coulomb criterion.The complete breakage of the crackelement and thus the nucleation of a discrete crack are accomplished after dissipating the material fracture energy release rate,Gc.Upon breakage of the cohesive surface,the crack element is removed from the simulation and therefore the model transition from a continuum to discontinuum is locally completed.A Coulomb-type friction is applied along every newly-created fracture.As the simulation progresses,f i nite displacements and rotations of discrete bodies are allowed and new contacts are automatically recognized(Munjiza and Andrews,1998).

Given the above modeling assumptions,the Y-Geo implementation of FDEM,rather than ELFEN’s approach,can be considered closer to a fully discrete method.In ELFEN,a real transition from a continuous elasto-plastic medium to a solid with discrete fractures is accomplished by dynamically inserting cracks into the model.Conversely,the material representation of Y-Geo resembles one of a particle-based DEM with rigid particles and deformable particle bonds replaced by deformable triangles and cohesive elements,respectively.

Fig.13.Simulation sequence of the EDZ formation process in a bedded rock using Y-Geo(after Lisjak(2013)).

3.2.2.Applications

EarlyapplicationsofY-Geo aimed atvalidating the adopted FDEM implementation in the context of the failure processes typically observed during standard rock mechanics tests on brittle rocks. Mahabadi et al.(2009)investigated the inf l uence of loading rate and sample orientation during a Brazilian test simulation on a layered rock.Mahabadi et al.(2010b)simulated the behavior of a homogeneous rock sample under biaxial loading conditions.The model captured the main phenomena observed in a triaxial test including localization of failure,fracture initiation and evolution,increase of strength with conf i nement,and brittle-ductile transition.Mahabadi et al.(2010a)showed good agreement between the experimental results of a high-strain-rate Brazilian disc test and Y-Geo simulation results in terms of tensile strength,failure time,and fracture mechanisms.Subsequently,the numerical experimentation with Y-Geo focused on the mechanical behavior of heterogeneous granitic rocks underdifferentloadingconditions.A procedure to incorporateactual micromechanicalinputparametersoftherock,togetherwiththereal distribution of mineral constituents,into a FDEM model was developed by Mahabadi et al.(2012b).Overall,the simulation results showed that by including accurate micromechanical parameters and the intrinsic rock geometric features,such as spatial phase heterogeneity and microcracks,the model can more accurately predict the mechanical responses of rock specimens under indirect tension (Mahabadi,2012).Moreover,heterogeneity was shown to play a key role in controlling the non-linear stress-strain behavior associated with the damage progress under compressive loading conditions (Fig.12a).Further validation of the same model was also carried out byconsideringtheacousticactivityreproducedduringthenumerical experiments(Lisjak et al.,2013).

More recently,the capabilities of Y-Geo were extended to capture the behavior of transversely isotropic rocks(Lisjak,2013;Lisjak et al.,2014a,b).The methodology was validated by investigating the laboratory-scale fracturing behavior of a clay shale,namely Opalinus Clay(Fig.12b),and the formation process of the excavation damaged zone(EDZ)around a test tunnel at the Mont Terri rock laboratory(Fig.13).Finally,Rougier et al.(2011)developed a 3D version of the Y-code of Munjiza(2004)and analyzed the effect of energy dissipation during the simulation of split Hopkinson pressure bar Brazilian experiments.

4.Concluding remarks

Modeling the failure process of brittle rocks represents a challenging task owing to several intrinsic features of the material mechanical behaviors,including strain localization,non-linear stressstrain response,and conf i nement dependent characteristics.At the rock mass scale,pre-existing discontinuities,such as faults and beddingplanes,contributetointroducingfurthercomplexityintotheproblem.ThisreviewtriedtosummarizetheuseofbothDEMs(either particle-or grain-based)and combined FDEM codes and their use to investigate the failure behavior of rocks under a variety of loading conditions.Theintroductionofbondsbetweendiscreteelementshas extendedtheapplicationoftheDEM,whichwasoriginallydeveloped to simulate the behavior of solids whereby pre-existing discontinuities have spacing comparable to the scale of interest of the problem under analysis(e.g.blocky rock masses,granular media),to capture the growth of new fractures.More recently,the FDEM,by combining fracture mechanicswithFEMand DEM,has emergedasanappealing alternative numerical tool for rock mechanics applications where an explicit consideration of fracture and fragmentation processes is of paramount importance.

Conf l ict of interest

We wish to con fi rm that there are no known con fl icts of interest associated with this publication and there has been no signi fi cant fi nancial support for this work that could have in fl uenced its outcome.

Alzo’ubi AK.Modeling of rocks under direct shear loading by using discrete element method.Alhosn University Journal of Engineering&Applied Sciences 2012;4: 5-20.

Amadei B.Importance of anisotropy when estimating and measuring in situ stresses in rock.International Journal of Rock Mechanics and Mining Sciences& Geomechanics Abstracts 1996;33(3):293-325.

Asadi MS,Rasouli V,Barla G.A bonded particle model simulation of shear strength and asperity degradation for rough rock fractures.Rock Mechanics and Rock Engineering 2012;45(5):649-75.

Bakun-Mazor D,Hatzor YH,Dershowitz WS.Modeling mechanical layering effects on stability of underground openings in jointed sedimentary rocks.International Journal of Rock Mechanics and Mining Sciences 2009;46(2):262-71.

Barla M,Beer G.Special issue on advances in modeling rock engineering problems. International Journal of Geomechanics 2012;12:617.

Baˇzant ZP,Oh BH.Crack band theory for fracture of concrete.RILEM Materials and Structures 1983;16(3):155-77.

Baˇzant ZP,Pijaudier-Cabot G.Nonlocal continuum damage,localization instability and convergence.Journal of Applied Mechanics 1988;55(2):287-93.

Benson PM,Vinciguerra S,Meredith PG,Young RP.Laboratory simulation of volcano seismicity.Science 2008;322(5899):249-52.

Bfer G.An isoparametric joint/interface element for f i nite element analysis.International Journal for Numerical Methods in Engineering 1985;21(4):585-600.

Biˊcaniˊc N.Fragmentation and discrete element methods.In:Milne I,Ritchie RO, Karihaloo B,editors.Comprehensive Structural Integrity.Oxford:Pergamon; 2003.pp.427-57.

Bieniawski ZT.Mechanism of brittle fracture of rock.Part I:theory of the fracture process.International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts 1967;4(4):405-6.

Billaux D,Dedecker F,Cundall P.A novel approach to studying rock damage:the three dimensional Adaptive Continuum/Discontinuum Code.In:Schubert W, editor.Proceedings of the ISRM Regional Symposium Eurock 2004 and the 53rd Geomechanics Colloquium.Salzburg:Austria;2004.

Blair SC,Cook NGW.Analysis of compressive fracture in rock using statistical techniques:part I.A non-linear rule-based model.International Journal of Rock Mechanics and Mining Sciences 1998;35(7):837-48.

Bobet A,Fakhimi A,Johnson S,Morris J,Tonon F,Yeung MR.Numerical models in discontinuous media:review of advances for rock mechanics applications. Journal of Geotechnical and Geoenvironmental Engineering,ASCE 2009; 135(11):1547-61.

Brace WF,Paulding Jr BW,Scholz C.Dilatancy in the fracture of crystalline rocks. Journal of Geophysical Research 1966;71(16):3939-53.

Cai M,Kaiser PK.Numerical simulation of the Brazilian test and the tensile strength of anisotropic rocks and rocks with pre-existing cracks.International Journal of Rock Mechanics and Mining Sciences 2004;41(Suppl.1):478-83.

Cai M.Fracture initiation and propagation in a Brazilian disc with a plane interface: a numerical study.Rock Mechanics and Rock Engineering 2013;46(2):289-302.

Cai M.Inf l uence of intermediate principal stress on rock fracturing and strength near excavation boundaries-insight from numerical modeling.International Journal of Rock Mechanics and Mining Sciences 2008;45(5):763-72.

Cho N,Martin CD,Sego DC.A clumped particle model for rock.International Journal of Rock Mechanics and Mining Sciences 2007;44(7):997-1010.

Christianson M,Board M,Rigby D.UDEC simulation of triaxial testing of lithophysal tuff.In:Proceedings of the 41st US Symposium on Rock Mechanics(USRMS). Golden,USA:American Rock Mechanics Association;2006.

Coggan JS,Pine RJ,Stead D,Rance JM.Numerical modelling of brittle rock failure using a combined f i nite-discrete element approach:implications for rock engineering design.In:Technology Roadmap for Rock Mechanics:the 10th ISRM Congress.Gauteng,South Africa:South African Institution of Mining and Metallurgy;2003.pp.211-8.

Cundall PA,Hart RD.Numerical modelling of discontinua.Engineering Computations 1992;9:101-13.

Cundall PA,Strack ODL.A discrete numerical model for granular assemblies.Geotechnique 1979a;29(1):47-65.

Cundall PA,Strack ODL.The distinct element method as a tool for research in granular media-part II.Rep.NSF Grant ENG76-20771.Minneapolis,USA: Department of Civil&Mineral Engineering,University of Minnesota;1979b.

Damjanac B,Board M,Lin M,Kicker D,Leem J.Mechanical degradation of emplacement drifts at Yucca Mountain-a modeling case study:part II:lithophysal rock.International Journal of Rock Mechanics and Mining Sciences 2007;44(3):368-99.

De Borst R,Crisf i eld MA,Remmers JJC,Verhoosel CV.Non-linear f i nite element analysis of solid and structures.2nd ed.Chichester,UK:John Wiley&Sons Ltd.; 2012.

De Borst R,Sluys LJ,Mühlhaus HB,Pamin J.Fundamental issues in f i nite element analysis of localization of deformation.Engineering Computations 1993;10(2): 99-122.

Diederichs MS.Manuel Rocha medal recipient:rock fracture and collapse under low conf i nement conditions.Rock Mechanics and Rock Engineering 2003;36(5): 339-81.

Dyszlewicz J.Micropolar theory of elasticity.New York:Springer;2004.

Eberhardt E,Stead D,Coggan JS.Numerical analysis of initiation and progressive failure in natural rock slopes-the 1991 Randa rockslide.International Journal of Rock Mechanics and Mining Sciences 2004;41(1):69-87.

Eberhardt E,Stead D,Stimpson B,Read RS.Changes in acoustic event properties with progressive fracture damage.International Journal of Rock Mechanics and Mining Sciences 1997;34(3/4).71.e1-71.e12.

Elmo D,Stead D.An integrated numerical modelling-discrete fracture network approach applied to the characterisation of rock mass strength of naturally fractured pillars.Rock Mechanics and Rock Engineering 2010;43(1):3-19.

Fakhimi A,Carvalho F,Ishida T,Labuz JF.Simulation of failure around a circular opening in rock.International Journal of Rock Mechanics and Mining Sciences 2002;39(4):507-15.

Fang Z,Harrison JP.Development of a local degradation approach to the modelling of brittle fracture in heterogeneous rocks.International Journal of Rock Mechanics and Mining Sciences 2002;39(4):443-57.

Feng XT,Pan PZ,Zhou H.Simulation of the rock microfracturing process under uniaxial compression using an elasto-plastic cellular automaton.International Journal of Rock Mechanics and Mining Sciences 2006;43(7):1091-108.

Ghaboussi J,Wilson EL,Isenberg J.Finite elements for rock joints and interfaces. Journal of the Soil Mechanics and Foundation Division,ASCE 1973;99(10): 849-62.

Goodman RE,Taylor RL,Brekke TL.A model for the mechanics of jointed rock. Journal of the Soil Mechanics and Foundation Division,ASCE 1968;94(4): 637-60.

Goodman RE.Introduction to rock mechanics.2nd ed.New York:John Wiley&Sons Ltd.;1989.

Hammah RE,Yacoub TE,Corkum B,Wibowo F,Curran JH.Analysis of blocky rock slopes with f i nite element shear strength reduction analysis.In:Eberhardt E, Stead D,Morrison T,editors.Proceedings of the 1st Canada-US Rock Mechanics Symposium.Vancouver,Canada;2007.pp.329-34.

Hammah RE,Yacoub T,Corkum B,Curran JH.The practical modelling of discontinuous rock masses with f i nite element analysis.In:Proceedings of the 42nd US Rock Mechanics Symposium and 2nd US-Canada Rock Mechanics Symposium.San Francisco,USA;2008.

Harthong B,Scholtès L,Donzé F.Strength characterization of rock masses,using a coupled DEM-DFN model.Geophysical Journal International 2012;191(2): 467-80.

Hatzor YH,Benary R.The stability of a laminated voussoir beam:back analysis of a historic roof collapse using DDA.International Journal of Rock Mechanics and Mining Sciences 1998;35(2):165-81.

Hatzor YH,Wainshtein I,Mazor DB.Stability of shallow karstic caverns in blocky rock masses.International Journal of Rock Mechanics and Mining Sciences 2010;47(8):1289-303.

Hazzard JF,Young RP.Simulating acoustic emissions in bonded-particle models of rock.International Journal of Rock Mechanics and Mining Sciences 2000;37(5): 867-72.

Hazzard JF,Collins DS,Pettitt WS,Young RP.Simulation of unstable fault slip in graniteusingabonded-particlemodel.PureandAppliedGeophysics 2002;159(1-3):221-45.

Hazzard JF,Young RP.Moment tensors and micromechanical models.Tectonophysics 2002;356(1-3):181-97.

Hazzard JF,Young RP.Dynamic modelling of induced seismicity.International Journal of Rock Mechanics and Mining Sciences 2004;41(8):1365-76.

Hillerborg A,Modéer M,Petersson PE.Analysis of crack formation and crack growth in concrete by means of fracture mechanics and f i nite elements.Cement and Concrete Research 1976;6(6):773-81.

Hoek E,Carranza-Torres CT,Corkum B.Hoek-Brown failure criterion-2002 edition. In:Proceedings of the 5th North American Rock Mechanics Symposium.Toronto,Canada;2002.pp.267-73.

Hoek E,Diederichs MS.Empirical estimates of rock mass modulus.International Journal of Rock Mechanics and Mining Sciences 2006;43(2):203-15.

Hoek E,Kaiser PK,Bawden WF.Support of underground excavations in hard rock. Taylor&Francis/A.A.Balkema;1995.

Hoek E.Practical rock engineering.North Vancouver,Canada:Evert Hoek Consulting Engineer Inc.;2006.

Hoek E.Strength of jointed rock masses.Geotechnique 1983;33(1):187-223.

Horii H,Nemat-Nasser S.Brittle failure in compression:splitting,faulting,and brittle-ductile transition.Philosophical Transactions of the Royal Society of London 1986;319(1549):337-74.

Itasca Consulting Group Inc..FLAC-fast Lagrangian analysis of continua.Minneapolis,USA:Itasca Consulting Group Inc.;2012a.

Itasca Consulting Group Inc..PFC2D(particle f l ow code in 2 dimensions).Minneapolis,USA:Itasca Consulting Group Inc.;2012b.

Itasca Consulting Group Inc..UDEC(universal distinct element code).Minneapolis, USA:Itasca Consulting Group Inc.;2013.

Jaeger JC,Cook NGW.Fundamentals of rock mechanics.2nd ed.London:Chapman& Hall;1976.

Jiang Y,Li B,Yamashita Y.Simulation of cracking near a large underground cavern in a discontinuous rock mass using the expanded distinct element method.InternationalJournalofRockMechanicsandMiningSciences 2009;46(1):97-106.

Jing L,Hudson JA.Numerical methods in rock mechanics.International Journal of Rock Mechanics and Mining Sciences 2002;39(4):409-27.

Jing L,Stephansson O.Fundamentals of discrete element methods for rock engineering:theory and applications.Amsterdam/Oxford:Elsevier;2007.

Jing L.A review of techniques,advances and outstanding issues in numerical modelling for rock mechanics and rock engineering.International Journal of Rock Mechanics and Mining Sciences 2003;40(3):283-353.

Kaiser PK,Kim BH.Rock mechanics challenges of underground constructions and mining.In:Proceedings of the Korean Rock Mechanics Symposium.Seoul, South Korea;2008.pp.1-6.

Karami A,Stead D.Asperity degradation and damage in the direct shear test:a hybrid FEM/DEM approach.Rock Mechanics and Rock Engineering 2008;41(2): 229-66.

Kazerani T,Yang ZY,Zhao J.A discrete element model for predicting shear strength and degradation of rock joint by using compressive and tensile test data.Rock Mechanics and Rock Engineering 2012;45(5):695-709.

Kazerani T,Zhao J.Micromechanical parameters in bonded particle method for modelling of brittle material failure.International Journal for Numerical and Analytical Methods in Geomechanics 2010;34(18):1877-95.

Kazerani T.Effect of micromechanical parameters of microstructure on compressive and tensile failure process of rock.International Journal of Rock Mechanics and Mining Sciences 2013;64:44-55.

Ke TC.Application of DDA to simulate fracture propagation in solid.In:Ohnishi Y, editor.Proceedings of the 2nd International Conference on Analysis of Discontinuous Deformation.Kyoto,Japan:Japanese Institute of Systems Research;1997.pp.155-85.

Kemeny J.Time-dependent drift degradation due to the progressive failure of rock bridges along discontinuities.International Journal of Rock Mechanics and Mining Sciences 2005;42(1):35-46.

Klerck PA,Sellers EJ,Owen DRJ.Discrete fracture in quasi-brittle materials under compressive and tensile stress states.Computer Methods in Applied Mechanics and Engineering 2004;193(27-29):3035-56.

Klerck PA.The f i nite element modelling of discrete fracture in quasi-brittle materials.PhD Thesis.Swansea,UK:University of Wales;2000.

Koo CY,Chern JC.Modelling of progressive fracture in jointed rock by DDA method. In:Ohnishi Y,editor.Proceedings of the 2nd International Conference on Analysis of Discontinuous Deformation.Kyoto,Japan:Japanese Institute of Systems Research;1997.pp.186-201.

Kozicki J,Donzé FV.A new open-source software developed for numerical simulations using discrete modelling methods.Computer Methods in Applied Mechanics and Engineering 2008;197(49/50):4429-43.

Kozicki J,Donzé FV.YADE-OPEN DEM:an open-source software using a discrete element method to simulate granular material.Engineering Computations 2009;26(7):786-805.

Lan H,Martin C,Hu B.Effect of heterogeneity of brittle rock on micromechanical extensile behaviour during compression loading.Journal of Geophysical Research:Solid Earth 2010;115(B1):1-14.

Lemos JV.Recent development and future trends in distinct element methods-UDEC/3DEC and PFC codes.In:Zhao J,Ohnishi Y,Zhao G,Sasaki T,editors. Advances in Discontinuous Numerical Methods and Applications in Geomechanics and Geoengineering.London:Taylor&Francis Group;2012.

Lin CT,Amadei B,Jung J,Dwyer J.Extensions of discontinuous deformation analysis for jointed rock masses.International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts 1996;33(7):671-94.

Lisjak A,Grasselli G,Vietor T.Continuum-discontinuum analysis of failure mechanisms around unsupported circular excavations in anisotropic clay shales.International Journal of Rock Mechanics and Mining Sciences 2014b;65:96-115.

Lisjak A,Liu Q,Zhao Q,Mahabadi OK,Grasselli G.Numerical simulation of acoustic emission in brittle rocks by two-dimensional f i nite-discrete element analysis. Geophysical Journal International 2013;195(3):423-43.

Lisjak A,Tatone BSA,Grasselli G,Vietor T.Numerical modelling of the anisotropic mechanical behaviour of Opalinus Clay at the laboratory-scale using FEM/DEM. Rock Mechanics and Rock Engineering 2014a;47(1):187-206.

Lisjak A.Investigating the inf l uence of mechanical anisotropy on the fracturing behaviour of brittle clay shales with application to deep geological repositories. PhD Thesis.Toronto,Canada:University of Toronto;2013.

Lockner DA,Byerlee JD,Kusenko V,Ponomarev A,Sidorin A.Quasi-static fault growth and shear fracture energy in granite.Nature 1991;350:39-42.

Lorig LJ,Cundall PA.Modeling of reinforced concrete using the distinct element method.In:Shah SP,Swartz SE,editors.Fracture of Concrete and Rock,SEMRILEM International Conference.Springer;1989.pp.276-87.

Ma GW,Wang XJ,Ren F.Numerical simulation of compressive failure of heterogeneous rock-like materials using SPH method.International Journal of Rock Mechanics and Mining Sciences 2011;48(3):353-63.

Mahabadi OK,Cottrell BE,Grasselli G.An example of realistic modelling of rock dynamics problems:FEM/DEM simulation of dynamic Brazilian test on Barre granite.Rock Mechanics and Rock Engineering 2010a;43(6):707-16.

Mahabadi OK,Lisjak A,Grasselli G,Lukas T,Munjiza A.Numerical modelling of a triaxial test of homogeneous rocks using the combined f i nite-discrete element method.In:Zhao J,Labiouse V,Dudt J,Mathier J,editors.Proceedings of the European Rock Mechanics Symposium(EUROCK)2010.A.A.Balkema;2010b.

Mahabadi OK,Grasselli G,Munjiza A.Numerical modelling of a Brazilian disc test of layeredrocksusingthecombinedf i nite-discreteelementmethod.In: Diederichs M,Grasselli G,editors.Proceedings of the 3rd Canada-US(CANUS) Rock Mechanics Symposium(RockEng09).Toronto,Canada;2009.

Mahabadi OK,Lisjak A,Munjiza A,Grasselli G.Y-Geo:new combined f i nite-discrete element numerical code for geomechanical applications.International Journal of Geomechanics 2012a;12:676-88.

Mahabadi OK,Randall NX,Zong Z,Grasselli G.A novel approach for micro-scale characterization and modelling of geomaterials incorporating actual material heterogeneity.Geophysical Research Letters 2012b;39(1).http://dx.doi.org/ 10.1029/2011GL050411.

Mahabadi OK.Investigating the inf l uence of micro-scale heterogeneity and microstructure on the failure and mechanical behaviour of geomaterials.PhD Thesis.Toronto,Canada:University of Toronto;2012.

Manouchehrian A,Marji MF.Numerical analysis of conf i nement effect on crack propagation mechanism from a f l aw in a pre-cracked rock under compression. Acta Mechanica Sinica 2012;28(5):1389-97.

Martin CD,Read RS,Martino JB.Observations of brittle failure around a circular test tunnel.International Journal of Rock Mechanics and Mining Sciences 1997; 34(7):1065-73.

Martin CD.Seventeenth Canadian Geotechnical Colloquium:the effect of cohesion loss and stress path on brittle rock strength.Canadian Geotechnical Journal 1997;34(5):698-725.

Mas Ivars D,Pierce ME,Darcel C,Reyes-Montes J,Potyondy DO,Young RP, Cundall PA.The synthetic rock mass approach for jointed rock mass modelling. International Journal of Rock Mechanics and Mining Sciences 2011;48(2): 219-44.

Mas Ivars D,Potyondy DO,Pierce M,Cundall PA.The smooth-joint contact model. In:Proceedings of the 8th World Congress on Computational Mechanics-5th European Congress on Computation Mechanics and Applied Science and Engineering.Venice,Italy;2008.

Moon T,Nakagawa M,Berger J.Measurement of fracture toughness using the distinct element method.International Journal of Rock Mechanics and Mining Sciences 2007;44(3):449-56.

Mühlhaus HB,Aifantis EC.A variational principle for gradient plasticity.International Journal of Solids and Structures 1991;28(7):845-57.

Mühlhaus HB,Vardoulakis I.The thickness of shear bands in granular materials. Geotechnique 1987;37(3):271-83.

Mühlhaus HB.Continuum models for layered and blocky rock.In:Hudson JA,editor. Comprehensive rock engineering.Oxford:Pergamon Press;1993.pp.209-30.

Munjiza A,Andrews KRF,White JK.Combined single and smeared crack model in combined f i nite-discrete element analysis.International Journal for Numerical Methods in Engineering 1999;44(1):41-57.

Munjiza A,Andrews KRF.NBS contact detection algorithm for bodies of similar size. International Journal for Numerical Methods in Engineering 1998;43(1):131-49.

Munjiza A,Andrews KRF.Penalty function method for combined f i nite-discrete element systems comprising large number of separate bodies.International Journal for Numerical Methods in Engineering 2000;49(11):1377-96.

Munjiza A,John NWM.Mesh size sensitivity of the combined FEM/DEM fracture and fragmentation algorithms.Engineering Fracture Mechanics 2002;69(2): 281-95.

Munjiza A,Owen DRJ,Bicanic N.A combined f i nite-discrete element method in transient dynamics of fracturing solids.Engineering Computations 1995;12(2): 145-74.

Munjiza A.The combined f i nite-discrete element method.Chichester,UK:John Wiley&Sons Ltd.;2004.

Owen DRJ,Feng YT.Parallelised f i nite/discrete element simulation of multifracturing solids and discrete systems.Engineering Computations 2001;18(3/ 4):557-76.

Pan XD,Reed MB.A coupled distinct element-f i nite element method for large deformation analysis of rock masses.International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts 1991;28(1):93-9.

Pande GN,Sharma KG.On joint/interface elements and associated problems of numerical ill-conditioning.International Journal for Numerical and Analytical Methods in Geomechanics 1979;3(3):293-300.

Paterson MS,Wong T.Experimental rock deformation-the brittle f i eld.New York: Springer;2004.

Pine RJ,Coggan JS,Flynn ZN,Elmo D.The development of a new numerical modelling approach for naturally fractured rock masses.Rock Mechanics and Rock Engineering 2006;39(5):395-419.

Pine RJ,Owen DRJ,Coggan JS,Rance JM.A new discrete fracture modelling approach for rock masses.Geotechnique 2007;57(9):757-66.

Potyondy DO,Cundall PA.Modeling notch-formation mechanisms in the URL mineby test tunnel using bonded.International Journal of Rock Mechanics and Mining Sciences 1998;35(4/5):510-1.

Potyondy DO,Cundall P.Bonded-particle simulations of the in-situ failure test at Olkiluoto.International Progress Report 01-13.Stockholm,Sweden:SKB;2000.

Potyondy DO,Cundall PA,Lee C.Modeling of rock using bonded assemblies of circular particles.In:Aubertin M,editor.Proceedings of the 2nd North American Rock Mechanics Symposium-NARMS’96.Brookf i eld,USA:A.A.Balkema; 1996.pp.1934-44.

Potyondy DO,Cundall PA.A bonded-particle model for rock.International Journal of Rock Mechanics and Mining Sciences 2004;41(8):1329-64.

Potyondy DO.A f l at-jointed bonded-particle material for hard rock.In:Proceedings of the 46th US Rock Mechanics/Geomechanics Symposium.Chicago,USA: American Rock Mechanics Association;2012.

Rasouli V,Harrison J.Assessment of rock fracture surface roughness using Riemannian statistics of linear prof i les.International Journal of Rock Mechanics and Mining Sciences 2010;47(6):940-8.

Riahi A,Hammah ER,Curran JH.Limits of applicability of the f i nite element explicit joint model in the analysis of jointed rock problems.In:Proceedings of the 44th U.S.Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium.Salt Lake City,USA;2010.

Rockf i eld Software Ltd..ELFEN 2D/3D numerical modelling package.Swansea,UK: Rockf i eld Software Ltd.;2004.

Rougier E,Knight EE,Sussman AJ,Swift RP,Bradley CR.The combined f i nite-discrete element method applied to the study of rock fracturing behaviour in 3D.In: Proceedings of the 45th US Rock Mechanics/Geomechanics Symposium.San Francisco,USA:American Rock Mechanics Association;2011.

Sagong M,Park D,Yoo J,Lee JS.Experimental and numerical analyses of an opening in a jointed rock mass under biaxial compression.International Journal of Rock Mechanics and Mining Sciences 2011;48(7):1055-67.

Scholtès L,Donzé F,Khanal M.Scale effects on strength of geomaterials,case study: coal.Journal of the Mechanics and Physics of Solids 2011;59(5):1131-46.

Scholtès L,Donzé F.Modelling progressive failure in fractured rock masses using a 3D discrete element method.International Journal of Rock Mechanics and Mining Sciences 2012;52:18-30.

Scholtès L,Donzé F.A DEM model for soft and hard rocks:role of grain interlocking on strength.Journal of the Mechanics and Physics of Solids 2013;61(2):352-69.

Sellers EJ,Klerck PA.Modelling of the effect of discontinuities on the extent of the fracture zone surrounding deep tunnels.Tunnelling and Underground Space Technology 2000;15(4):463-9.

Shi G,Goodman R.Discontinuous deformation analysis-a new method for computing stress,strain and sliding of block systems.In:Proceedings of the 29th US Symposium on Rock Mechanics.Rotterdam:A.A.Balkema;1988.

ˇSmilauer V,Catalano E,Chareyre B,Dorofenko S,Duriez J,Gladky A,Kozicki J, Modenese C,Scholtès L,Sibille L,Stránský J,Thoeni K.Yade documentation. URL:http://yade-dem.org/doc/;2010.

Stefanizzi S,Barla G,Kaiser PK,Grasselli G.Numerical modeling of rock mechanics tests in layered media using a fi nite/discrete element approach.In:Proceedings of the 12th International Conference of International Association for Computer Methods and Advances in Geomechanics(IACMAG).Goa,India;2008.

Stefanizzi S.Numerical modelling of strain-driven fractures around tunnels in layered rock masses.PhD Thesis.Turin,Italy:Politecnico di Torino;2007.

Tang C.Numerical simulation of progressive rock failure and associated seismicity. International Journal of Rock Mechanics and Mining Sciences 1997;34(2): 249-61.

Tang CA,Lü HY.The DDD method based on the combination of RFPA and DDA.In: Chen G,Ohnishi Y,Zheng L,Sasaki T,editors.Frontiers of Discontinuous Numerical Methods and Practical Simulations in Engineering and Disaster Prevention.London:Taylor&Francis Group;2013.pp.105-12.

Tannant DD,Wang C.Thin tunnel liners modelled with particle fl ow code.Engineering Computations 2004;21(2-4):318-42.

Vyazmensky A,Elmo D,Stead D.Role of rock mass fabric and faulting in the development of block caving induced surface subsidence.Rock Mechanics and Rock Engineering 2010a;43(5):533-56.

Vyazmensky A,Stead D,Elmo D,Moss A.Numerical analysis of block cavinginduced instability in large open pit slopes:a fi nite element/discrete element approach.Rock Mechanics and Rock Engineering 2010b;43(1):21-39.

Wanne TS,Young RP.Bonded-particle modelling of thermally fractured granite. International Journal of Rock Mechanics and Mining Sciences 2008;45(5): 789-99.

WanneTS.Bonded-particlesimulationoftunnelsealingexperiment.In: Diederichs M,Grasselli G,editors.ROCKENG09:Proceedings of the 3rd CANUS Rock Mechanics Symposium.Toronto,Canada;2009.

Wilson EL.Finite elements for foundations,joints and fl uids.In:Gudehus G,editor. Finite Elements in Geomechanics.Chichester,UK:John Wiley&Sons Ltd.;1977. Yan M.Numerical modelling of brittle fracture and step-path failure:from laboratory to rock slope scale.PhD Thesis.Burnaby,Canada:Simon Fraser University; 2008.

Yuan SC,Harrison JP.A review of the state of the art in modelling progressive mechanical breakdown and associated fl uid fl ow in intact heterogeneous rocks. International Journal of Rock Mechanics and Mining Sciences 2006;43(7): 1001-22.

Zhang XP,Wong LNY.Cracking processes in rock-like material containing a single fl aw under uniaxial compression:a numerical study based on bonded-particle model approach.Rock Mechanics and Rock Engineering 2012;45(5):711-37.

Zhang XP,Wong LNY.Crack initiation,propagation and coalescence in rock-like material containing two fl aws:a numerical study based on bonded-particle model approach.Rock Mechanics and Rock Engineering 2013;46(5):1001-21.

Zhao Z.Gouge particle evolution in a rock fracture undergoing shear:a microscopic DEM study.Rock Mechanics and Rock Engineering 2013;46(6):1461-79.

*Corresponding author.Tel.:+1 416 978 0125.

E-mailaddresses:andrea.lisjak@gmail.com(A.Lisjak),giovanni.grasselli@ utoronto.ca(G.Grasselli).

Peer review under responsibility of Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.

Numerical modeling

Discrete element method(DEM)

Finite-discrete element method(FDEM)