Fracture initiation and propagation in intact rock-A review

E.Hoek,C.D.Mrtin

aWest Vancouver,British Columbia,V7V 0B3,Canada

bDepartment of Civil&Environmental Engineering,University of Alberta,Edmonton,Alberta,T6G 2W2,Canada

Fracture initiation and propagation in intact rock-A review

E.Hoeka,C.D.Martinb,*

aWest Vancouver,British Columbia,V7V 0B3,Canada

bDepartment of Civil&Environmental Engineering,University of Alberta,Edmonton,Alberta,T6G 2W2,Canada

A R T I C L E I N F O

Article history:

Received 29 April 2014

Received in revised form

7 June 2014

Accepted 10 June 2014

Available online 24 June 2014

Tensile failure

Crack propagation

Griff i th theory

Hoek-Brown criterion

Tension cutoff

Crack coalescence

Numerical models

The initiation and propagation of failure in intact rock are a matter of fundamental importance in rock engineering.At low conf i ning pressures,tensile fracturing initiates in samples at 40%-60%of the uniaxial compressive strength and as loading continues,and these tensile fractures increase in density,ultimately coalescing and leading to strain localization and macro-scale shear failure of the samples.The Griff i th theory of brittle failure provides a simplif i ed model and a useful basis for discussion of this process.The Hoek-Brown failure criterion provides an acceptable estimate of the peak strength for shear failure but a cutoff has been added for tensile conditions.However,neither of these criteria adequately explains the progressive coalition of tensile cracks and the f i nal shearing of the specimens at higher conf i ning stresses.Grain-based numerical models,in which the grain size distributions as well as the physical properties of the component grains of the rock are incorporated,have proved to be very useful in studying these more complex fracture processes.

©2014 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

1.Introduction

In order to understand the characteristics of rock and rock masses as engineering materials,it is necessary to start with the behavior of intact rock.From an engineering point of view,this involves studying laboratory-scale samples,such as diamond drill core,with dimensions in the range of 50 mm diameter.For many rock types,the grain size is small enough that samples of this scale can be considered homogeneous and isotropic.

The characteristics that will be discussed in the following text are the strength and deformation characteristics of intact rock.As illustrated in Fig.1,a number of stress states need to be considered and,as is common in most discussions on this topic,it will be assumed that these stress states can be considered in two dimensions.In other words,it is assumed that the intermediate principal stressσ2has a minimal inf l uence on the initiation and propagation of failure in the samples.While some authors consider this tobe an over-simplif i cation,a full three-dimensional treatment of the topic would result in complex text which would defeat the purpose of this presentation which is designed to be as clear and understandable as possible.

2.Theoretical fracture initiation:background

2.1.Griff ith tensile theory

Griff i th(1921)proposed that tensile failure in brittle materials such as glass initiates at the tips of minute defects which he represented by f l at elliptical cracks.His original work dealt with fracture in material subjectedtotensile stress butlaterhe extended this concept to include biaxial compression loading(Griff i th,1924).The equation governing tensile failure initiation in a biaxial compressive stress f i eld is

whereσtis the uniaxial tensile strength of the material.Note that tensile stresses are negative.

Murrell(1958)proposed the application of Griff i th theory to rock.In the 1960s,Griff i th’s two-dimensional theory was extended to three dimensions by a number of authors including Murrell (1958),Sack and Kouznetsov whose work was summarized in books on brittle failure of rock materials by Andriev(1995)andPaterson and Wong(2005).These extensions involve examining the stresses induced around open penny-shaped cracks in a semiinf i nite body subjected to triaxial compressive stressesσ1,σ2and σ3.It was shown that the intermediate principal stressσ2has no signif i cant inf l uence on the crack tip stresses inducing tensile failure initiation.Hence,this criterion is essentially equivalent to loading a penny-shaped crack in a biaxial stress f i eld,as shown in Fig.2.

The equation governing tensile failure initiation is

Fig.1.Typical failure characteristics of intact rock plotted in terms of major and minor principal stresses and Mohr circles and envelope.

Fig.2.Tensile crack propagation from an inclined elliptical Griff i th crack in a biaxial compressive stress f i eld.

Note that,whereas the original Griff i th theory predicts a ratio of compressive to tensile strengthσc/|σt|=8,the penny-shaped crack version predictsσc/|σt|=12.The corresponding Mohr envelope for the penny-shaped crack version is

whereσcis the uniaxial compressive strength of the material.

The Griff i th theory deals only with the initiation of tensile failure.It cannot be extended to deal with failure propagation and eventual shear failure in compression.However,under certain conditions when tensile stresses exceed the tensile strength,tensile failure initiation can lead to crack propagation.In these cases the tensile cracks propagate along the major principal stress(σ1)trajectory as shown in Fig.2.

2.2.Modif ications to Griff ith theory for closed cracks

The original Griff i th theory was derived from analyses of crack initiation at or near the tips of open elliptical cracks.In the case of rocks,most of the defects from which tensile cracks originate are grain boundaries which are usually cemented and have to be considered as closed cracks.McClintock and Walsh(1962)proposed that tensile fracture from closed Griff i th cracks can be predicted on the basis of the conventional Mohr-Coulomb equation: whereφis the angle of friction andτ0is the shear strength at zero normal stress.

Hoek(1965)discussed the transition from the Griff i th theory for open cracks,which applies for conf i ning stressesσ3＜0,and the modif i ed theory for closed cracks which applies for compressive conf i ning stresses.For the principal stress plot,this transition occurs atσ3=0,while for the Mohr envelope,the transition occurs at the tangent points on the Mohr circle representing the uniaxial compressive strengthσcof the intact rock.The transition is illustrated in Fig.3 in which the principal stress plots are shown for friction angles of 35°,45°and 55°.

A much more comprehensive discussion on this topic is given in Paterson and Wong(2005)but the plotted results are essentially the same as those shown in Fig.3.Hence,for the purpose of this discussion,Eq.(4)above is adequate.

Zuo et al.(2008)examined the growth of microcracks in rocklike materials on the basis of fracture mechanics considerations. They assumed a sliding-crack model which generates wing cracks, similar to those shown in Fig.2,from close to the crack tips when the frictional strength of the sliding surfaces is overcome.They found that the failure initiation criterion can be expressed by the following equation:

whereμis the coeff i cient of frictionwhich is equal to the tangent of the friction angle,i.e.μ=tanφ.

The coeff i cientκis used for mixed mode fracture and it can be derived from various approximations based on a maximum stress criterion or a maximum energy release criterion(Zuo et al.,2008).Plots for Eq.(5),whenμ=0.7,1 and 1.43 (φ=35°,45°and 55°),κ=1 andσc/|σt|=12,are included in Fig.3.Note that the same transition from open to closed crack behavior has been assumed as for the Mohr-Coulomb criterion (Eq.(4))discussed above.

Fig.3.Principal stress plots for various criteria for tensile failure initiation from closed cracks in brittle materials such as rock.

2.3.Length of induced tensile cracks

Hoek(1965)carried out experiments inwhich f l at open“cracks”were machined ultrasonically into annealed glass plates which werethen loaded biaxially.The initiation of tensile cracks fromnear the tips of these simulated cracks,as predicted by Griff i th’s original theory,was conf i rmed.However,it was found that the length of the tensile cracks was limited by the ratio of the applied biaxial stresses σ3/σ1.As reported by Cho et al.(2007),theoretical studies on closed cracks have been carried out by several authors including Ashby and Hallam(1986),Kemeny and Cook(1987),Germanovich and Dyskin(1988),Martin(1997)and Cai et al.(1998).These studies, the results of which are plotted in Fig.4,conf i rm the importance of conf i nement in limiting the length of induced tensile cracks from pre-existing f l aws in brittle materials subjected to compressive loading.Fig.5 summarizes some of this information in a different form and shows a principal stress plot and Mohr’s diagram for open penny-shaped cracks subjected to different biaxial compressive stress loadings.

2.4.Summary

Griff i th theory of brittle fracture initiation and its modif i cations have been discussed in hundreds of technical papers.A particularly useful review was presented by Fairhurst(1972)which is recommended reading for anyone interested in pursuing this topic in greater depth.While there can be no dispute that this is very important background material for an understanding of themechanics of brittle failure initiation,it is of limited practical value in the f i eld of rock engineering.

Fig.4.Dependence of length of tensile cracks on principal stress ratioσ3/σ1.

Fig.5.Plots of principal stresses def i ning tensile failure initiation from open pennyshaped cracks in a homogeneous isotropic elastic solid loaded biaxially.

This is because an isolated Griff i th crack in a semi-inf i nite plate is an inadequate model of the grain boundary network in which tensile failure originates and propagates in intact rock as shown in Fig.6.This photograph shows that,while it would always be possible to f i nd a critically oriented grain boundary from which tensile failure could initiate,it is unlikely that the induced crack would follow the path suggested in Fig.2 for homogeneous isotropic materials.Rather,the tensile crack path would follow a path dictated bygrain boundaries with only isolated cracks running across intact grains.This means that we have to explore other more complicated models in order to fully understand the fracture process in rock.

Before leaving the topic of Griff i th theory and its modif i cations, it is worth summarizing what we have learned from the discussion given earlier since the same or similar issues will apply to the numerical analysis of fracture initiation and propagation:

(1)The brittle failure process initiates and is,to a very large extent, controlled by the tensile strength of intact rock or of its component grains.

(2)The initiation of tensile cracks at or near the tip of a Griff i th crack,whether this crack is open or closed,depends upon the orientation of the Griff i th crack in relation to the applied stresses.Fracture will initiate at or close to the tip of a critically oriented crack when the conditions def i ned by Eqs.(1)-(5)are satisf i ed,depending upon the assumptions made in deriving these equations.

Fig.6.Crack path in a specimen of Witwatersrand Quartzite from a deep gold mine in South Africa,sectioned after uniaxial compressive loading to about 75%of the uniaxial compressive strength. Photograph reproduced from Hoek and Bieniawski(1965).

(3)This process isextremelysensitivetothe degreeof conf i nement and the extent of failure reduces quickly as the minor principal stress(σ3)increases fromσ3=σttoσ3＞0,as shown in Figs.1 and 5.

(4)At some level of conf i nement,in the range ofσ3/σ1≈0.2,tensile failure can be suppressed completely and the peak strength of the intact rock is controlled by shear failure for higher conf i nement.

(5)For applications to conf i ned rock materials,the closed Griff i th crack model(Eqs.(4)and(5))is the most appropriate.The shear strength of the conf i ned defects(typicallygrain boundaries)is a controlling parameter in the initiation and propagation of the tensile failure.

(6)The ratio of uniaxial compressive to tensile strength(σc/|σt|)is an important parameter in understanding the failure of rock and similar brittle materials.

3.Fracture initiation and propagation:laboratory tests

3.1.Peak strength and the Hoek-Brown criterion

Hoek and Brown(1980)and Hoek(1983)described the development of the Hoek-Brown failure criterion as a trial-and-error process using the Griff i th theory as a starting point.They were seeking an empirical relationship that f i tted observed shear failure conditions for brittle rock subjected to triaxial compressive stresses.The equation chosen to represent the failure of intact rock was

wheremiis a material constant.

Zuoetal.(2008)pointedoutthatthesubstitutionof（μ/κ）（σc/|σt|）=miin their failure criterion(Eq.(5))leads to the Hoek-Brown criterion for intact rock(Eq.(6)).They suggested that the constantmiis not simply an empirical constant but that it has real physical meaning.

During the 1970s,when the Hoek-Brown criterion was developed,there was little interest in the tensile strength of rock and,in fact,it was frequently assumed to be zero.The emphasis was on conf i ned shear failure which was assumed to control the stability of the relatively small slopes and shallow tunnels that were constructed at the time.However,with the increase in depth of excavations in civil and mining engineering projects and the depth of boreholes in oil exploration and recovery,the issue of the tensile strength of rock became increasingly important.In particular,the process of brittle fracture which results in splitting,popping, spalling and rockbursting in pillars and tunnels,and“breakouts”in boreholes is a tensile failure process which is not adequately dealt with by the Hoek-Brown failure criterion.Simply projecting the Hoek-Brown equation(Eq.(6))back to itsσ3intercept withσ1=0 does not give an acceptable value for the tensile strength of the rock.

Ramseyand Chester(2004)and Bobich(2005)haveinvestigated this issue in a series of experiments in which they used dogboneshaped specimens as shown in Fig.7.By choosing appropriate diameters for the ends and center of the specimen and by adjusting the values of the conf i ning pressurePcand the axial stressPa,a range of values ofσ3andσ1can be generated in the test section.

The results of tests on Carrara marble are reproduced in Fig.8. The Hoek-Brown criterion(Eq.(6))has been f i tted to the shear data obtained in these tests and the resulting curve has been projected back to give an intercept ofσ3=-17.2 MPa forσ1=0.As can be seen in Fig.8,this does not correspond to the tensile failure datawhich gives an average tensile strengthσ3=-7.75 MPa.In other words,the Hoek-Brown criterion has no provision for predicting the tensile strength shown in Fig.8,and highlighted by the“Tension cutoff”.

Fig.7.Dogbone-shaped specimen used by Ramsey and Chester(2004)to investigate tensile failure of Carrara marble.

3.2.Fairhurst’s generalized Griff ith fracture criterion

Fairhurst(1964)proposed that the Griff i th failure criterion, discussed in Section 2 of this paper,could be generalized in termsof the ratio of compressive to tensile strengthσc/|σt|as follows(a detailed derivation is given in the Appendix):

(1)Ifw(w-2)σ3+σ1≤0,failure occurs whenσ3=σt;

(2)Ifw(w-2)σ3+σ1≤0,failure occurs when

Fig.8.Results from conf i ned extension tests and triaxial compression tests by Ramsey and Chester(2004).

Fitting Eq.(7)to the results plotted in Fig.8 gives the combined plot shown in Fig.9.

Reliable direct tensile test data on rock are very rare and the authors have only been able to assemble the limited number of results included in Table 1.However,by f i tting both Hoek-Brown and Fairhurst curves to these data,as shown in Fig.9,it has been possible to arrive at a preliminary relationship between the Fairhurst tension cutoff(def i ned byσc/|σt|)and the Hoek-Brown parametermiplotted in Fig.10.While more work remains to be done on this topic,particularly more tests of the type carried out by Ramsey and Chester(2004)and Bobich(2005),the authors suggest that Fig.10 provides a useful practical tool for estimating a tensile cutoff for the Hoek-Brown criterion.

Examination of Table 1 shows that,for lowmivalues,the Hoek-Brown criterion over-estimates the tensile strength compared with the Fairhurst criterion.However,formi＞25 the Hoek-Brown criterion under-estimates the tensile strength by an amount that is generally small enough to be ignored for most engineering applications.

Hoek(1965)assembled a signif i cant quantity of laboratory triaxial test data for a variety of rock types and concrete and these results(peak strength values)are plotted in a dimensionless form in Fig.11.It can be seen that individual data sets plot on parabolic curves and that a family of such curves,covering all of the shear data collected,can be generated for different values of the Hoek-Brown constantmi.The constantmiis an indicator of the brittleness of the rock with weaker and more ductile rocks having lowmivalues while stronger and more brittle rocks have highmivalues.A few data points forσ3＜0 are included in Fig.11 and these are dealt with adequately by the tension cutoff discussed above.

Fig.9.Combined plot of Hoek-Brown and Fairhurst failure criteria with tension cutoff.

Table 1Analysis of data containing reliable tensile values.

3.3.Interpretation of laboratory triaxial tests

In order to understand the application of the Hoek-Brown failure criterion to intact rock behavior,it is useful to consider a practical example which involves uniaxial and triaxial tests on specimens of Lac du Bonnet granite from the site of the Atomic Energy of Canada Limited Underground Research Laboratory at Pinawa in Manitoba,Canada(Read and Martin,1991).The specimen preparation and testing were carried out by the CANMET Mining and Mineral Sciences Laboratories in Ottawa,Canada,which has a long-standing international reputation for high quality testing services.

Using strain and acoustic emission measurements,Lau and Gorski(1992)determined the crack initiation,onset of strain localization and peak strengths for each conf i ning pressure in a series of triaxial tests carried out in a servo-controlled stiff testing machine,based on the procedure summarized in Fig.12(Martin and Chandler,1994).The results of these tests are plotted in Fig.13.The Hoek-Brown failure criterion(Eq.(6))has been f i tted to each data set and the f i tted parameters are included inTable 2.Note that,because themivalue for the peak strength is 32.4,no correction has been made for the measured tensile strength,as discussed above.

It is clear from Figs.12 and 13 that fracturing in laboratory samples is a complex process and that simply measuring the peak stress does not capture this fracturing process.However,it is also clear fromFig.13 that we can def i ne the boundaries for this process, i.e.fracture initiation,onset of fracture localization and collapse peak stress.In the next section,a numerical approach that can simulate this process is examined.

Fig.10.Relationship betweenσc/|σt|andmifrom Table 1.

Fig.11.Dimensionless plot of triaxial test results from laboratory tests on samples from a wide range of rock types and concrete.

3.4.Numerical approaches

Since the early 1980s,there has been an exponential growth in the sophistication and power of numerical programs which have been increasingly applied to the study of failure initiation and propagation processes in soil,rock and concrete.Fig.14 illustrates two phenomenological approaches that are typically used to replicate the failure process numerically.The early approaches often used the sliding-crack model to capture many of the elements discussed in the earlier section on Griff i th theory.More recently, there has been an increasing focus on the force-chain crack model using discrete element formulations(Fig.14).A small selection of some of the more signif i cant papers in this latter f i eld includes: Cundall and Strack(1979),Diederichs(1999,2003),Potyondy and Cundall(2004),Pierce et al.(2007),Lorig(2007),Cho et al. (2007),Cundall et al.(2008),Lan et al.(2010),Potyondy(2012) and Scholtès and Donzé(2013).

PotyondyandCundall(2004)pointedoutthatsystems composed of many simple objects commonly exhibit behavior that is much more complicated than that of the constituents.They listed the following characteristics that need to be considered in developing a rock mass model:

(1)Continuously nonlinear stress-strain response,with ultimate yield,followed by softening or hardening.

(2)Behavior that changes in character,according to stress state; for example,crack patterns quite different in tensile,unconfi ned-and con fi ned-compressive regimes.

(3)Memory of previous stress or strain excursions,in both magnitude and direction.

(4)Dilatancy that depends on history,mean stress and initial state.

(5)Hysteresis at all levels of cyclic loading/unloading.

(6)Transition from brittle to ductile shear response as the mean stress is increased.

(7)Dependence of incremental stiffness on mean stress and history.

(8)Induced anisotropy of stiffness and strength with stress and strain path.

(9)Nonlinear envelope of strength.

(10)Spontaneous appearance of microcracks and localized macro fractures.

(11)Spontaneous emission of acoustic energy.

Fig.12.Stages in the progressive failure of intact rock specimens subjected to compressive loading. Modif i ed from Martin and Christiansson(2009).

Within the limitations of this document,it is clearly not feasible to present a summary of the many approaches that have been adopted in the numerical modeling of intact rock fracture initiation and propagation.Nor it is possible to judge the extent to which the requirements outlined above by Potyondy and Cundall(2004)have been met in these studies.A most useful DEM(discrete element method)approach is considered to be that given by Lan et al.(2010) who presented results of a study of fracture initiation and propagation in Äspö diorite and Lac du Bonnet granite.The mineral grain structures for these two crystalline rocks are shown in Fig.15.

The program UDEC(Itasca,2013)was used in this study and a Voronoi tessellation scheme was employed to create polygonal structures which closely simulated the mineral grain structures shown in Fig.15.Each grain has a unique identity,location and material type and the average grain size distribution has also been simulated in these models.The properties of the principal grain minerals(plagioclase,K-feldspar and quartz with biotite in the Lac du Bonnet granite and with chlorite in the Äspö diorite)were exported to an ASCII f i le which was then imported into the UDEC model using the FISH internal macro-language.The model geometry is then created automatically in UDEC and the grains are made deformable by discretizing,each polygon using triangular zones. These deformable grains,which were unbreakable in the Lan et al. (2010)study,are then cemented together along their adjoining sides as shown in Fig.16.

Fig.17 shows the results of two uniaxial compression tests carried out by Lan et al.(2010)on UDEC models of Äspö diorite andLac du Bonnet granite.The stress-strain response,the crack initiation stress(σci),the crack damage stressσcdand the peak stressσfshow excellent agreement with those def i ned from laboratory tests on Äspö diorite by Staub and Andersson(2004)and on Lac du Bonnet granite by Martin and Chandler(1994).

Fig.13.Tensile crack initiation,strain localization and peak strength for Lac du Bonnet granite from tests by Lau and Gorski(1992).

Fig.14.Two models commonly used to simulate cracking observed in heterogeneous assemblages of polygonal shaped minerals.Modif i ed from Nicksiar and Martin(2013).

The paper by Lan et al.(2010)is a good example of the application of numerical modeling to the study of fracture initiation and propagation in intact rock and is recommended reading for anyone interested in this f i eld.Much more work is required to bring this approach to maturity.

Professor E.T.Brown,in a foreword to the scoping study for the application of numerical methods to mass mining wrote:“In my opinion,the development of the bonded particle model based on the PFC and PFC3D distinct element codes by Dr.Peter Cundall and his co-workers at Itasca represents one of the most signif i cant contributions made to modern rock mechanics research.It is now well established that this model has the ability to reproduce the essential,and some more subtle,features of the initiation and propagation of fracturing in rocks and rock masses.”Numerical modeling has now progressed beyond the original bonded particle models developed by Itasca but Brown’s comments remain valid as we look ahead to the research that remains to be done on thesecomplexfundamentalprocessesoffailureinitiationand propagation.

Table 2Results of triaxial tests on Lac du Bonnet granite.

A word of warning.In the rush to get into print,many authors have published papers on numerical modeling in which pictures of fracture propagation in Brazilian disk tests or uniaxial compression tests have been included as a demonstration of the validity of the numerical approach used.It is relatively easy to produce results which appear to be credible for these tests but,unfortunately,in many cases the numerical methods used are immature and fail when applied to more complex problems.

In the following section,we brief l y consider two approaches that may be used to evaluate fracture initiation and propagation in situ.The process is commonly referred to as spalling.

Fig.15.Example of mineral grain structure observed in polarized light thin section.(a)Äspö diorite.Width of the image is 4 mm(modif i ed from Lampinen(2006)).(b)Lac du Bonnet granite.Combined polarized and f l uorescent microscope image of specimen from Underground Research Laboratory in Canada.Width of image is 4 mm(modif i ed from Åkesson(2008)).Images reproduced from Lan et al.(2010).

4.Fracture initiation and propagation in situ:spalling

There are two practical issues associated with spalling:(1) identifying the conditions that will initiate spalling,and(2) def i ning the extent and depth of spalling.The results from two well-documented in situ experiments in crystalline rock are used to examine these practical issues.

Fig.16.Layout for an unconf i ned compression test for a Lac du Bonnet granite sample and an Äspö diorite sample using the UDEC model.The different gray scales indicate the degree of mineral grain strength.Higher strength grains have a darker color.Reproduced from Lan et al.(2010).

4.1.Test tunnel of the URL Mine-by experiment

Martin et al.(1997)have described spalling observed in a test tunnel(Fig.18)in massiveLac du Bonnet granite at a depth of 420 m below surface in the Underground Research Laboratory.The intent of the experiment was to study the damage resulting from stress redistribution associated with the full-face mining of 3.5 m diameter tunnel.The mining was carried out using line drilling and rock splitters to avoid the potential for blasting-induced damage.This technique allowed full-face 1-m advance increments.

An extensive program of in situ stress measurements was carried out at this site and the rock mass surrounding the test tunnel. The in situ rock mass stresses at this location were a sub-vertical stressσv=11 MPa and a sub-horizontal stress ofkσv=60 MPa, inclined at 11°to the horizontal,with an intermediate subhorizontal stress of 44 MPa.

Fig.17.Calibrated stress-strain response with laboratory data for(a)Äspö diorite and (b)Lac du Bonnet granite.The drawings at the right show the damage pattern of the specimen.Images reproduced from Lan et al.(2010).

The spalling which occurred afterexcavation of the testtunnel is illustrated in Fig.19.This spalling occurred as a relatively gentle fracture process during the excavation advance.The full extent ofthe spalling was onlyevident once the tunnel had been cleaned and loose spall remnants removed by scaling.When these remnants were removed in the f l oor,it was suff i cient to trigger minor amounts of new spalling,suggesting the important role of small conf i ning stress in controlling the spalling process.

Fig.20 shows the zone of potentialspalling for the Lac du Bonnet granite in which the test tunnel was mined as well as the stress changes associated with the tunnel excavation.The measured in situ stresses,denoted by pointAin Fig.20,are equal to the principal stressesσ1=60 MPa andσ3=11 MPa in the rock before the tunnel was mined.The 11°inclination of the stress f i eld can be ignored in the discussion which follows.After excavation,the minor principal stress in the tunnel wall is reduced toσ3=0.The maximum principalstressonthetunnelroofandf l oorisgivenby σmax=3σv(k-1)=169 MPa.These stressesareplotted as pointBin Fig.20.

These roof and f l oor stresses fall just above the curve def i ning strain localization and well above the tensile failure initiation curve.Martin and Christiansson(2009)concluded that in the absence of in situ results,the laboratory crack initiation stress(see Fig.13)could be taken as a lower bound for the spalling strength. More recently,Nicksiar and Martin(2013)compiled the crack initiation stress for a range of rock types.The results are illustrated in Fig.21 and demonstratethe consistencyof tensile crack initiation observed in laboratory tests.Using a spalling initiation criterion based on this approach is a useful f i rst step and supported by recent experience.Diederichs et al.(2010)implemented this approach in a continuum model with good success.

Knowing that spalling may occur,the next step is to establish the severity of the failure.The depth of the notch created by spalling is dependent upon the ratio of the maximum boundary stress to the uniaxial compressive strength(peak)orσmax/σcas shown in Fig.22(Martin et al.,1999).In the case of the test tunnel under discussion here,this ratio is 169/227=0.74 and hence the notch depth is approximately 0.3-0.4 times the tunnel radius according to Fig.22.

Experience with the application of the trend line in Fig.22 indicates that the uniaxial compressive strength should be the mean uniaxial compressive strength value(Rojat et al.,2009).Determining the mean uniaxial compressive strength may appear straightforward.The scatter in the values for 13 samples of Lac du Bonnet granite is shown in Fig.23.Notice that the mean value of 211 MPa is less than theσcvalue of 227 MPa given in Table 2 using the Hoek-Brown equations.This is a typical f i nding and in this case ref l ects the effect of the microcracks common in Lac du Bonnetgranite.Despite the suggestions in the ISRM Suggested Methods, conducting uniaxial tests requires signif i cant care in order to reduce the effect of uneven and/or misaligned sample ends.Simply conducting a large number of tests is no substitute for properly preparing the samples,and in many cases can be misleading as the mean value often decreases as the number of samples increases, due to poor quality control with sample preparation.

Fig.18.Layout of the Mine-by experiment at the 420 m level of the Underground Research Laboratory.Modif i ed from Martin and Read(1996).

Fig.19.Spalling in the roof and f l oor of a circular test tunnel in the Underground Research Laboratory at Pinawa in Manitoba,Canada.Photo courtesy of AECL.

Fig.20.Def i nition of the zone of potential spalling in massive Lac du Bonnet granite, from Fig.13.The changes in the stresses in the rock surrounding the tunnel are also shown as pointsAandBin this plot.

Figs.24 and 25 show examples of mild spalling and severe rockbursting in underground excavations,representing the extremes of the process under discussion here.Practical experience suggests that shallow spalls are generally associated with pure tensile failure which causes thin slivers or plates of rock to peel off the tunnel surface.These occur with little“popping”and,once the maximum depth of the spall has been achieved,they remain stable provided that there are no changes in the surrounding stress f i eld due,for example,to excavation of adjacent openings.

Deeper spalls,such as that in the Mine-by tunnel described above,are somewhat more complicated in that shear failure probably becomes involved as the notch tip moves away from the excavation boundary.Numerical analyses of this failure process have proved to be extremely challenging and it has to be said that much work remains to be done before the complex interaction of tensile and shear processes associated with deep spall notches can be predicted with any degree of conf i dence.

Rockbursts,such as that illustrated in Fig.25,are probably associated with conditions in which the maximum induced boundary stress approaches the uniaxial compressive strength of the surrounding massive rock.These events involve implosion of the rock into the tunnel with the release of signif i cant amounts ofenergy.The authors are not aware of any currently available numerical tools that offer any credible means of explaining or predicting the rockburst process.

Fig.21.Tensile crack initiation in various rocks. Modif i ed from Nicksiar and Martin(2013).

Fig.22.Observed spalling notch depths plotted against the ratio of maximum boundary stress to uniaxial compressive strength(Martin et al.,1999).

Fig.23.Example of the distribution of uniaxial compressive strength for 13 samples of Lac du Bonnet granite.

Fig.25.Severe rockbursting in an access tunnel in a deep level gold mine in South Africa.

4.2.Numerical simulation of spalling

The approach described above to estimate the onset and depth of spalling is a reasonable f i rst step.But to make progress in the support interaction needed for tunnel design,proper numerical approaches are needed.While this is still an on-going research topic,one approach that goes from the laboratory calibration to spall prediction is described brief l y below.

The nuclear industry in Finland and Sweden is preparing for the construction of a geological repository for used nuclear fuel at a depth of about 450 m.Their concept requires excavation of 1.75-m-diameter 8-m-deep boreholes and spalling is a design issue that must be addressed.Andersson et al.(2009)described and reported the results of a full-scale experiment(APSE)that examined the development of spalling around two of the large diameter boreholes.The APSE experiment was carried out at the 450-m level of the Äspö Hard Rock Laboratory in southern Sweden.Lan et al.(2013)described how the UDEC modeling work originally described by Lan et al.(2010)was used to model the spalling process.Fig.26 shows the model conf i guration and the grain-scale geometry.The approach and the properties of the grains and the contacts were exactly the same as that given in Lan et al.(2010).

The APSE experiment was unique because the magnitude of the stresses on the boundary of the large boreholes was controlled by excavation-induced and thermally induced stresses.The experiment demonstrated that in situ experiments could follow the same loading conditions and control that are normally associated with laboratory tests.

The conf i guration of the experiment allowed the boundary stresses to be applied gradually.This facilitated observing the spalling process at different stages.Fig.27 provides comparison of the results from the UDEC model with the visual observations at two loading stages.An important conclusion from the APSE work is that the f i ndings related to fracture initiation and propagation that were observed in the Mine-by test tunnel in massive un-fractured granite were applicable to the fractured water-bearing rock mass of the APSE experiment.

The approach described by Lan et al.(2010,2013)demonstrated that the properties of the laboratory tests can be used to evaluate the in situ spalling process when coupled with numerical approaches that capture all stages of brittle failure,i.e.from fracture initiation through to fracture propagation.While this approach holds much promise,it is still limited to two dimensions,and much work needs to be done before this approach becomes state of practice.

5.Conclusions

Our understanding of initiation and propagation of fracturing in intact rock has resulted from detailed analysis of the stress-strain data from laboratory-scale samples with dimensions in the range of 50 mm diameter.At low conf i ning pressures,tensile fracturing initiates in these samples at 40%-60%of the uniaxial compressive strength and as loading continues,these tensile fractures increase in densityand ultimatelycoalesce,leading to strain localization and macro-scale shear failure of the sample.The Griff i th theory of brittle failure provides a simplif i ed model assuming that allfractures initiate from the tips of inclined f l aws,namely grain boundaries in the sliding-crack model.The Hoek-Brown failure envelope is used to capture the collapse load associated with this localized macro-scale shear fracture.However,it has been necessary to add a tension cutoff,based on a generalized fracture theory proposed by Fairhurst(1964)in order to accommodate the tensile failure observed in detailed laboratory tests.

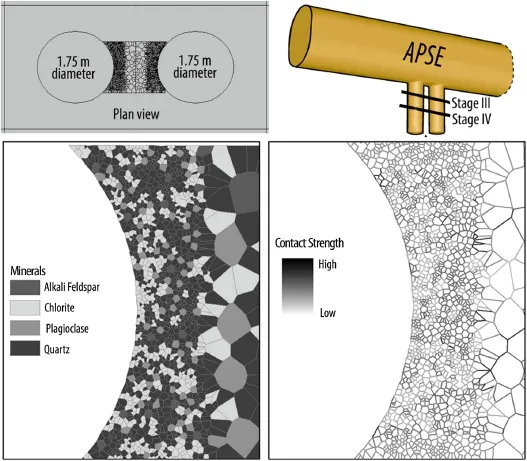
Fig.26.Grain-based UDEC model developed by Lan et al.(2010)and used to simulate the spalling process observed by Andersson et al.(2009). Modif i ed from Lan et al.(2013).

Fracture initiation while tensile in nature is more diff i cult to be modeled.With the improvements in computing power,the discrete element codes have shown that the force-chain crack model is a viable alternative to explain the tensile fracture initiation coalition of tensile cracks and the f i nal shearing of the specimens at higher conf i ning stresses.Grain-based numerical models,based on the discrete element formulation,in which the grain size distributions as well as the physical properties of the component grains of the rock are incorporated,have proved to be very useful in studying these complex processes.They have also demonstrated that the approach based on laboratory processes is useful for capturing spalling,the in situ process of fracture initiation and coalescence. While this approach holds much promise,the current grain-based models are still limited to two dimensions,and much research needs to be carried out before this approach becomes state of practice.

Fig.27.Modeled damage at stages III and IV compared with observation.Modeling result shows the distribution of tensile cracking and shear cracking at different damage stages.The photograph and illustration are modif i ed from Lan et al.(2013).

Conf l ict of interest

The authors wish to conf i rm that there are no known conf l icts of interest associated with this publication and there has been no signif i cant f i nancial support for this work that could have inf l uenced its outcome.

Acknowledgments

The contribution of Dr.Connor Langford in deriving the solution to the generalized fracture criterion proposed by Fairhurst(1964)is gratefully acknowledged.This derivation is presented in the Appendix.

Professor Ted Brown reviewed the f i nal manuscript and offered a number of valuable comments,which are also acknowledged.

Appendix

According to the generalized Fairhurst criterion:

(1)Ifw(w-2)σ3+σ1≤0,failure occurs whenσ3=σt;

(2)Ifw(w-2)σ3+σ1≤0,failure occurs when

σ1can be written by

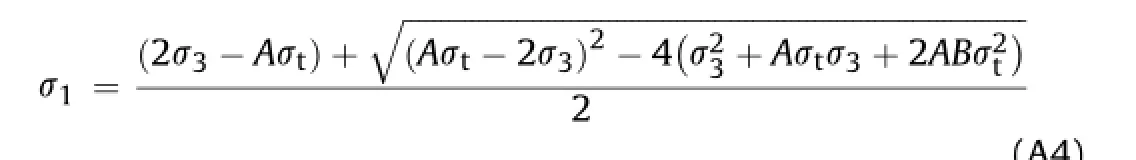
Åkesson U.Characterization of micro cracks using core disking.SKB Report P-08-103.Stockholm:Swedish Nuclear Fuel and Waste Manage Co.;2008.p.43.

Andersson J,Martin CD,Stille H.The Äspö pillar stability experiment:Part II-rock mass response to coupled excavation-induced and thermal-induced stresses. International Journal of Rock Mechanics&Mining Sciences 2009;46(5):879-95.

Andriev GE.Brittle failure of rock materials.Rotterdam:A.A.Balkema;1995.

Ashby MF,Hallam D.The failure of brittle solids containing small cracks under compressive stress.Acta Metallurgica 1986;34(3):497-510.

Bobich JK.Experimental analysis of the extension to shear fracture transition in Berea sandstone.MS Thesis.Texas,USA:Texas A&M University;2005.

Brace WF.Brittle fracture of rocks.In:Judd WR,editor.State of stress in the earth’s crust.New York:American Elsevier;1964.pp.111-80.

Cai M,Kaiser PK,Martin CD.A tensile model for the interpretation of microseismic events near underground openings.Pure and Applied Geophysics 1998;153: 67-92.

Cho N,Martin CD,Sego DS.A clumped particle model for rock.International Journal of Rock Mechanics and Mining Sciences 2007;44(7):997-1010.

Cundall PA,Strack O.A discrete numerical model for granular assemblies.Geotechnique 1979;29(1):47-65.

Cundall PA,Pierce ME,Mas Ivars D.Quantifying the size effect of rock mass strength.In:Potvin Y,Carter J,Dyskin A,Jeffrey R,editors.Proceedings of the1st southern hemisphere international rock mechanics symposium.Nedlands, Western Australia:Australian Centre for Geomechanics;2008.pp.3-15.

Diederichs MS,Carter T,Martin CD.Practical rock spall prediction in tunnels.In: Proceedings of ITA World Tunnel Congress;2010.pp.1-8.Vancouver,(CDROM).

Diederichs MS.Instability of hard rockmasses:the role of tensile damage and relaxation.PhD Thesis.Waterloo,Canada:University of Waterloo;1999.

Diederichs MS.Rock fracture and collapse under low conf i nement conditions.Rock Mechanics and Rock Engineering 2003;36(5):339-81.

Fairhurst C.On the validity of the“Brazilian”test for brittle materials.International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts 1964;1(4):535-46.

Fairhurst C.Fundamental considerations relating to the strength of rock.In:Colloquium on rock fracture.Bochum,Germany:Ruhr Universitat;1972.Updated in 2004 and available from http://www.itascacg.com.

Germanovich JN,Dyskin AV.A model of brittle failure for material with cracks in uniaxial loading.Mechanics of Solids 1988;23(2):111-23.

Griff i th AA.The phenomena of rupture and f l ow in solids.The Philosophical Transactions of the Royal Society London(Series A)1921;221:163-98.

Griff i th AA.Theory of rupture.In:Proceedings of the 1st international Congress of applied mechanics.Delft:Tech.Boekhandel en Drukkerij J Walter Jr;1924. pp.55-63.

Hoek E.Rock fracture under static stress conditions.Pretoria,South Africa:Council for Scientif i c and Industrial Research Report MEG 383;1965.

Hoek E,Bieniawski ZT.Brittle fracture propagation in rock under compression. International Journal Fracture Mechanics 1965;1(3):137-55.

Hoek E,Brown ET.Empirical strength criterion for rock masses.Journal of the Geotechnical Engineering Division,ASCE 1980;106(9):1013-35.

Hoek E.The strength of jointed rock masses.Geotechnique 1983;33(3):187-223.

Itasca.UDEC 5.00 software reference manual.Minneapolis:Itasca;2013.

Kemeny JM,Cook NGW.Crack models for the failure of rock under compression.In: Desai CS,Krempl E,Kiousis PD,Kundu T,editors.Proceedings of the 2nd international conference constitutive laws for engineering materials,theory and applications,vol.1.London:Elsevier Science Publishing Co;1987.pp.879-87.

Lampinen H.Äspö Pillar Stability Experiment.Detailed geological mapping of pillar blocks.SKB Report IPR-05-24.Stockholm,Sweden:Swedish Nuclear Fuel and Waste Manage,Co.;2006.p.67.

Lan H,Martin CD,Andersson JC.Evolution of in situ rock mass damage induced by mechanical-thermalloading.RockMechanicsandRockEngineering 2013;46(1):153-68.

Lan H,Martin CD,Hu B.Effect of heterogeneity of brittle rock on micromechanical extensile behavior during compression loading.Journal of Geophysical Research 2010;115:B01202.http://dx.doi.org/10.1029/2009JB006496.

Lau JSO,Gorski B.Uniaxial and triaxial compression tests on URL rock samples from boreholes 207-045-GC3 and 209-069-PH3.CANMET Divisional Report MRL 92 -025(TR);1992.p.46.

Lorig LJ.Using numbers from geology.In:Proceedings of the 11th Congress of the international society for rock mechanics.London:Taylor and Francis;2007. pp.1369-77.

Martin CD,Chandler NA.The progressive fracture of Lac du Bonnet granite.International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts 1994;31(6):643-59.

Martin CD,Read RS.AECL’s Mine-by experiment:a test tunnel in brittle rock.In: Aubertin M,Hassani F,Mitri H,editors.Proceedings of the 2nd North American rock mechanics symposium,vol.1.Rotterdam:A.A.Balkema;1996.pp.13-24.

Martin CD,Read RS,Martino JB.Observations of brittle failure around a circular test tunnel.InternationalJournalofRockMechanicsandMiningSciences 1997;34(7):1065-73.

Martin CD.The effect of cohesion loss and stress path on brittle rock strength. Canadian Geotechnical Journal 1997;34(5):698-725.

Martin CD,Kaiser PK,McCreath DR.Hoek-Brown parameters for predicting the depthofbrittlefailurearoundtunnels.CanadianGeotechnicalJournal 1999;36(1):136-51.

Martin CD,Christiansson R.Estimating the potential for spalling around a deep nuclear waste repository in crystalline rock.International Journal of Rock Mechanics and Mining Sciences 2009;46(2):219-28.

McClintock FA,Walsh JB.Friction on Griff i th cracks in rock under pressure.In: Proceedings of the 4th US national Congress on applied mechanics,vol.2.New York:Am.Soc.Mech.Eng.;1962.pp.1015-21.

Murrell SAF.The strength of coal under tri-axial compression.In:Walton WH, editor.Mechanical properties of non-metallic brittle materials.London:Butterworth Scientif i c Publications;1958.pp.123-45.

Nicksiar M,Martin CD.Crack initiation stress in low porosity crystalline and sedimentary rocks.Engineering Geology 2013;154:64-76.

Paterson MS,Wong TF.Experimental rock deformation-the brittle f i eld.2nd ed. New York:Springer-Verlag;2005.

Pierce M,Mas Ivars D,Cundall P,Potyondy D.A synthetic rock mass model for jointed rock.In:Eberhardt E,Stead D,Morrison T,editors.Proceedings of Canada-U.S.rock mechanics symposium,vol.1.London:Taylor&Francis Group; 2007.pp.341-9.

Potyondy DO,Cundall PA.A bonded particle model for rock.International Journal of Rock Mechanics and Mining Sciences 2004;41(8):1329-64.

Potyondy DO.The bonded-particle model as a tool for rock mechanics research and application:current trends and future directions.In:Proceedings of the 7th Asian rock mechanics symposium,ARMS7.Seoul:ARMS;2012.pp.1-33.

Ramsey J,Chester F.Hybrid fracture and the transition from extension fracture to shear fracture.Nature 2004;428:63-6.

Read RS,Martin CD.The underground research laboratory Mine-by experiment-a research perspective on tunnel design.Canadian Tunnelling 1991:75-88.

Rojat F,Labiouse V,Kaiser PK,Descoeudres F.Brittle rock failure in the Steg Lateral Adit of the Lötschberg base tunnel.Rock Mechanics and Rock Engineering 2009;42(2):341-59.

Scholtès L,Donzé FV.A DEM model for soft and hard rocks role of grain interlocking on strength.Journal of the Mechanics and Physics of Solids 2013;61(2):352-69.

Staub I,Andersson JC.Äspö pillar stability experiment geology and mechanical properties of the rock in TASQ.SKB Report R-04-0.Stockholm:SvenskaKärnbränslehantering AB;2004.

Zuo JP,Li HT,Xie HP,Ju Y,Peng SP.A nonlinear strength criterion for rock-like materials based on fracture mechanics.International Journal of Rock Mechanics and Mining Sciences 2008;45(4):594-9.

Evert Hoekgraduated with a BSc and MSc in mechanical engineering from the University of Cape Town(1955 and 1958)and became involved in the young science of rock mechanics in 1958 when he started working in research on the problems of brittle fracture associated with rockbursts in very deep mines in South Africa.His degrees include a PhD from the University of Cape Town,a DSc (Eng.)from the University of London and honorary doctorates from the Universities of Waterloo and Toronto in Canada.He has been elected as a Fellow of the Royal Academy of Engineering(UK),a Foreign Associate of the US National Academy of Engineering and a Fellow of the Canadian Academy of Engineering.He was Reader and then Professor of Rock Mechanics at the Imperial College of Science and Technology in London(1966-1975),a Principal of Golder Associates in Vancouver(1975-1987),Industrial Research Professor of Rock Engineering at the University of Toronto in Canada(1987-1993)and an independent consulting engineer based in Vancouver,Canada(1993-2013).He retired in 2013.His consulting work included major civil and mining projects in 35 countries around the world and has involved rock slopes,dam foundations,hydroelectric projects,underground caverns and tunnels excavated conventionally and by TBM.

*Corresponding author.

E-mailaddresses:ehoek@xsmail.com(E.Hoek),derek.martin@ualberta.ca (C.D.Martin).

Peer review under responsibility of Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.