机器人运动学逆解及奇异和多解的处理

叶上高，刘电霆

(桂林理工大学机械与控制工程学院，广西桂林541004)

机器人运动学逆解，即根据工具坐标系相对于基坐标系的目标位姿，求解机器人各关节角。逆运动学在机器人学中占有非常重要的地位，是机器人轨迹规划和运动控制的基础，直接影响着控制的快速性与准确性［1］。一般机器人运动学逆解算法可分为以下几种［2］:解析法(又称反变换法)、几何法和数值解法。由PAUL 等提出的反变换法求解过程直观，因而被广泛采纳，但其求解过程中需多次进行齐次变换矩阵的逆运算和4 ×4 维矩阵的乘积运算，导致求解过程复杂耗时［3］。

大多数工业机器人的几何结构都满足Pieper 准则［4］，即3 个相邻关节轴交于一点或相互平行，其运动学逆解可以得到数量一定的若干组封闭解。对于最后3 个关节为旋转关节而且轴线相交于一点的六自由度机器人，其前3 个关节决定末端执行器的位置，后3 个关节决定末端执行器的姿态［5］。故文中以其中的典型代表——ABB 公司的IRB2600 机器人为研究对象，提出了一种有别于传统方法的位姿分离逆解算法，根据末端执行器的位置矢量计算前3 个关节变量，利用末端执行器的旋转矩阵计算后3 个关节角。此算法逆解过程完全避免了矩阵求逆和4 ×4 维矩阵相乘的运算，过程直观，因此，比一般的解析算法更加简单高效，便于实时控制。此外，文中对逆解所涉及的奇异和多解问题的处理也进行了详细分析。最后，用ADAMS 对该逆解算法的正确性进行了仿真验证。

1 运动学正解

IRB2600 为6R 机构，采用D-H 方法［6］，建立连杆坐标系如图1所示。

图1 IRB2600 机器人的连杆坐标系

IRB2600 机器人的D-H 参数如表1所示。

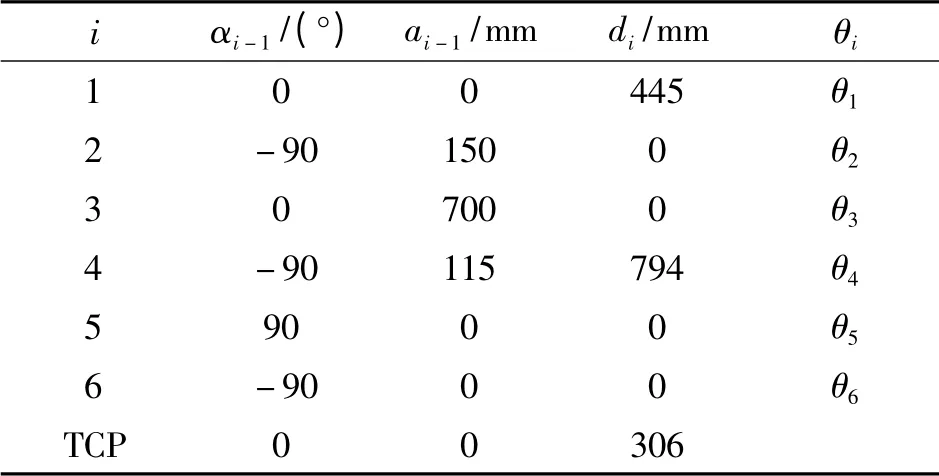
表1 IRB2600 机器人的D-H 参数

由此求得各连杆变换矩阵后连乘得机器人腕点的齐次变换矩阵

2 运动学逆解算法

2.1 前3 个关节角

求θ1。因a1+a3c23－d4s23+a2c2正负未定，故由式(2)、(3)求得θ1有两个可能解

θ1A=arctan2(wy，wx)，θ1B=arctan2(－wy，－wx)

求θ2。若c1≠0，由式(2)、(4)整理得

将式(6)和(7)等号两边平方后取和，整理得

若c1=0，为避免分母为0，则改用式(3)、(4)用同样的方法求解。

求θ3。若c1≠0，因θ1和θ2已求得，则由式(2)、(4)整理所得的式(6)、(7)两式等号左边已知，即式(6)和(7)构成二元一次方程组，可解得未知数为

其中:l1=k1－a2c2，l3=k3+a2s2

故θ3=Atan2(s23，c23)－θ2。若c1=0，为避免分母为0，则改用式(3)、(4)用同样方法求解。

2.2 后3 个关节角

因前3 个角和式(5)已求得，故上式等号左边已知。

求θ5。由c5=r'23得

求θ4。由－c4s5=r'13及s4s5=r'33，得

求θ6。由c6s5= r'21及－ s5s6= r'22，用与θ4相同的方法求取。

3 奇异点

若式(1)中wx和wy都为0，则θ1的变化不影响腕点的位置，故为奇异点。若式(8)算出的θ2的两个可能解相等，则连杆坐标系原点连线O2O3与O3O4共线，故为奇异点。若式(9)解得θ5为零，则关节4 和6 的转轴共线，故为奇异点［7］。

4 逆解中多解问题的处理步骤

逆解可能存在多解，而机器人的控制需要唯一的确切解。若不考虑避障要求，可按如下步骤获取唯一最优解。首先，若关节角的求解表达式的值域不能完全包含该关节运动范围，则在必要情况下，需将求得的关节角可能解加减360°，补出关节运动范围内的其他可能解［8］;其次，剔除关节运动范围以外的可能解;最后，由运动连续性［9］，选取与该关节角上一时刻的值距离最近的可能解为唯一最优解。各关节角的求解顺序为:先确定θ1的唯一最优解，再利用θ1的最优解按前述逆解方法和多解处理步骤求取θ2的最优解。其余关节角的求取顺序依此类推。最后所得的这组唯一的最优关节角即可作为实现机器人目标位姿的控制依据。

表2 IRB2600 机器人的关节活动范围

5 算法仿真验证

在ADAMS 中建立IRB2600 机器人模型进行逆解算法的仿真验证。保持不变，使TCP 在t∈［0，40］沿螺旋线x =944 +400cost，y=－400sint，z=1 354－20t 运动，在t∈(40，50］从该螺旋线终点沿直线回到螺旋线起点。t =0 时刻关节角初始值为θ1=0，θ2=－0.988 6 rad，θ3=－1.178 rad，θ4=0，θ5=1.381 1 rad，θ6=0 rad。ADAMS 仿真过程中关节角的测量结果为图2 中的实线，用文中方法逆解所得关节角变化曲线在图2 中用叉号表示。由图2 可见逆解结果与仿真结果完全重合，证明该算法正确有效。仿真过程中t =40 s 时刻的截图见图3。

图2 逆解结果与仿真结果对照图

图3 仿真过程中t=40 s 时刻的截图

6 结论

仿真证明文中提出的逆解算法正确有效。逆解过程比一般的解析算法更加简单高效，便于实时控制，对其他机器人的逆解也具有一定参考意义。

【1】刘华山，朱世强，吴剑波，等.基于奇异摄动理论的输入有界机器人轨迹跟踪控制［J］.控制理论与应用，2009，26(12):1371－1377.

【2】王其军，杜建军.MOTOMAN 机器人逆运动学新分析［J］.哈尔滨工业大学学报，2010，42(3):451－454.

【3】PAUL R P.Robot Manipulators:Mathematics，Programming，andControl［M］.Cambridge:MIT Press，1981.

【4】PAUL R P，SHINANO B E.Kinematical Control Equations for SimpleManipulators［J］.IEEE Trans SMC，1981，11(6):449－455.

【5】GOLDENBERG A A，BENHABIB B，FENTON R G.A Complete Generalized Solution to the Inverse Kinematics of Robots［J］.IEEE Journal of Robotics and Automation，1985，1(1):14－20.

【6】JORGE Angeles.Fundamentals of Robotic Mechanical Systems［M］.New York:Spriger-Verlag，2003.

【7】杨武，蒋梁中.排爆机器人机械手运动规划［J］.机械设计与制造，2008(5):184－186.

【8】刘华山，朱世强，吴剑波，等.基于向量内积的机器人实时逆解算法［J］.农业机械学报，2009，40(6):212－216，207.

【9】胡杰，张铁.SCARA 机器人控制系统的设计与研究［J］.机械设计与制造，2012(5):162－163.