基于模糊算法的水下机器人路径规划研究

王妹婷，陆柳延，齐永锋，吕学智，蒋伟，李生权

(扬州大学能源与动力工程学院，江苏扬州225127)

水下机器人是一种工作于水下的极限作业机器人，由于水下工作环境具有复杂性和不确定性，提高自主式水下机器人智能化的关键环节——路径规划研究显得尤为重要。常用的局部路径规划算法有势场法、A*算法、栅格法及模糊算法［1－3］。考虑到水下环境的复杂性，测距声呐所得的环境信息都是近似、不完善的，并伴有一定的噪声干扰［4］，而模糊控制器的最大优点就是能够采用输入的模糊信息［5］进行控制。此外，水下机器人的动力学模型极其复杂，是一个典型的非线性系统［6］。针对这类特殊控制对象，提出了一种结合视线导航原理［7］和模糊算法的未知环境下水下机器人实时路径规划策略，应用该策略，可于障碍物环境中，自动寻找一条从起始点到目标点的无碰撞路径。

依据障碍物的不同形状大小，采用不同方式求取机器人与障碍物之间距离以及目标点、机器人与障碍物三者之间的夹角［8］。此外，在MATLAB 仿真中，根据障碍物特征，对模糊控制规则表进行修改:障碍物较小时，以路径最短最平滑为主;障碍物较大时，以严格快速避开障碍物为主。

1 工作原理

假设水下机器人匀速运动，首先，通过短基线系统，实时得到机器人与目标预定点的相对位置信息;利用测距声呐对其运动前方的±90°范围内进行实时探测，得到环境信息［9］。实时计算机器人与障碍物最近点的距离d，以及障碍物最近点、水下机器人、目标点三者间的夹角α，如图1所示。通过模糊控制器进行实时模糊推理，得到避障状态下水下机器人所需转动的偏转角，从而使得水下机器人有效地避开障碍物，安全到达设定目标点。

图1 视线导航原理图

1.1 距离d 的求取

与工作环境尺寸相比，障碍物尺寸较小的情况下，障碍物大小、形状均可忽略不计，视为一个点，距离d 为机器人与该障碍物两点之间的距离，公式为:

其中，(xr，yr)为机器人当前坐标，(xo，yo)为障碍物坐标。

反之，当障碍物尺寸较大且形状不规则时，根据障碍物的边缘坐标信息，近似变换为矩形障碍物，如图2所示，得到矩形的4 个坐标点，以方便求取水下机器人与障碍物的最小距离点。

图2 不规则图形矩形化

矩形障碍物上距离水下机器人最近点与两者相对位置有关，为求取水下机器人与矩形障碍物最近点的距离，针对机器人位于矩形障碍物的8 个区域分别讨论，如图3所示。

矩形障碍物与水下机器人之间的最近距离点可表示为:水下机器人位于1 区域，即xr≤xmin，yr≤ymin时，最近距离点d_node 坐标为(xmin，ymin);水下机器人位于2 区域，即xmin＜xr≤xmax，yr≤ymin时，d_node坐标为(xr，ymin);水下机器人位于3 区域，即xr＞xmax，yr≤ymin时，d_node 坐标为(xmax，ymin);水下机器人位于4 区域时，即xr≥xmax，ymin＜yr≤ymax时，d_node 坐标为(xmax，yr);水下机器人位于5 区域，即xr≥xmax，yr＞ymax时，d_node 坐标为(xmax，ymax);水下机器人位于6 区域，即xmin≤xr＜xmax，yr≥ymax时，d_node 坐标为(xr，ymax);水下机器人位于7 区域，即xr＜xmin，yr≥ymax时，d_node 坐标为(xmin，ymax);水下机器人位于8 区域，即xr≤xmin，ymin＜yr＜ymax时，d_node 坐标为(xmin，yr)。

水下机器人与矩形障碍物间的距离转化为水下机器人与实时得到的矩形障碍物上最近距离点两点之间的距离:

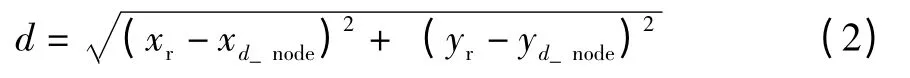
图3 水下机器人与矩形障碍物的相对位置示意图

1.2 夹角α 的求取

通过机器人当前位置、障碍物位置、目标位置三点坐标，能够得到夹角α。因机器人的避障环境为其运动前方的±90°范围内，将连接机器人与目标点的导航线作为分界线，当障碍物在导航线左侧时设α为正;反之，α 为负。故

式中:a 为机器人与实时障碍物最近点的距离;b 为机器人与目标点的距离;c 为实时障碍物最近点与目标点的距离。

2 模糊控制器研究

基于模糊算法的水下机器人避障控制系统如图4所示，其中模糊控制器由模糊量化、模糊规则、模糊推理和反模糊化接口4 部分组成［10］。由短基线系统得到目标的位置信息，由多个测距声呐实时测得的与障碍物的距离信息，经过信息融合计算后所得到的距离d，以及障碍物与机器人、目标的夹角α，同时作为模糊控制器的输入。输入量经过模糊控制器进行模糊推理，最终得到水下机器人的偏转角φ，然后水下机器人以新的方向进行运动。

图4 水下机器人避障控制系统示意图

此处采用最简单的信息融合技术，即每个方向的距离信息中，取其中较小的一个数据作为该方向的输入，然后在每个方向上提取的距离信息中取最小的作为这一时刻的距离信息。

2.1 模糊集、模糊论域及隶属函数确立

模糊控制输入为水下机器人与障碍物的最小距离d、两视线导航角的夹角α，输出为水下机器人在t时刻所需的偏转角φ。

由于测距声呐的测量距离达30 m，系统设定的障碍物影响距离d 为10 m，即d 的论域为［0，100］，用模糊语言定义的模糊集为 D ={VS，S，M，B，VB }。其中，VS 表明距离极小，VB 表明距离极大。

为了判断障碍物相对于目标的位置，设定障碍物、机器人、目标三者夹角α 的论域为［－ 90°，90°］，用模糊语言定义的模糊集为α = {NL，NS，Z，PS，PL}。其中，Z 表明障碍物在导航线上，N表示负，即设定的障碍物在导航线右侧，反之，P 表示障碍物在导航线左侧;L 表示角度大，S 则表示角度小。输出偏转角φ 设定为向左转为负，向右转为正，偏转角φ 的论域为［－45°，45°］，同样用模糊语言定义的模糊集为α= {NL，NS，Z，PS，PL}。

根据输入输出的模糊论域设定合适的模糊语言变量，在此均采用三角形隶属度函数来反应模糊集合的模糊性。

2.2 模糊控制规则库的建立与模糊推理

水下机器人在恒速运动过程中的避障原则为:在障碍物的影响距离范围内，当障碍物在航线左侧时，机器人向右侧绕行，当障碍物在航线上或者右侧时，机器人向左侧绕行;除此之外，机器人沿着导航线，向目标方向前进。

依据障碍物的不同尺寸大小，提出以下两种控制器设计要求:当障碍物大小在整个工作环境下可忽略不计时，以路径能够实现平滑最短为主，防止水下机器人频繁过大的角度偏转导致的振荡;当障碍物较大的情况下，由于水下机器人运动速度比较快，所以在测出障碍物的同时就应开始偏转，以免机器人无法安全绕行。因此，设定两套控制规则，分别如表1、表2所示，并在仿真过程中，根据障碍物的大小，调节控制器中输出偏转角的大小及障碍物影响距离，可更好地完成机器人避障要求。

表1 障碍物较小时偏转角φ 的模糊规则表

表2 障碍物较大时偏转角φ 的模糊规则表

模糊推理是是模糊控制器的核心，在此采用Mamdani 推理，用中心面积法去模糊化［11］，最终得到水下机器人所需的偏转角。

3 仿真研究

3.1 仿真实验流程

为了验证所提出的算法能否满足水下机器人的避障要求，在MATLAB 中进行了仿真实验。仿真针对的水下机器人以恒速运动，运动步长l =1 mm，分别在障碍物近似为点的情况及障碍物较大且不规则的情况下进行仿真，仿真步骤如图5所示。在仿真过程中，设计的仿真实验平台不仅能够交互式地任意设置机器人起点和终点位置，还能交互式地任意设置障碍物的数量、大小、形状和位置，可以更好地检验算法的可行性和通用性。

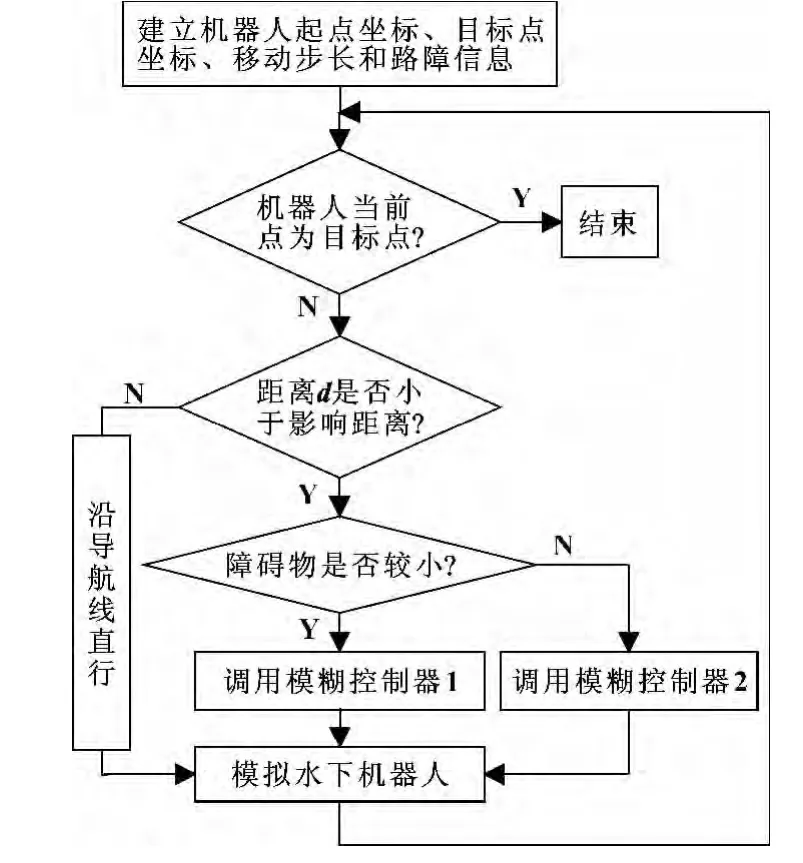
图5 基于模糊算法的机器人避障流程

3.2 仿真结果分析

通过交互式界面建立机器人起点坐标、目标点坐标、路障信息后，当该障碍物较小时，采用模糊控制器1，对应的模糊控制规则如表1所示。当障碍物对水下机器人的最小影响距离为d=100 mm，输出偏转角φ= ［－45°，45°］时，得到图6 中的路径1。由于在整个水下机器人避障设计过程中，提出在实现避障功能的同时，能够尽可能的实现路径最短且平滑。所以，在仿真过程中，设置障碍物对水下机器人的最小影响距离为d =50 mm，输出偏转角φ = ［－20°，20°］时，得出图6 中的路径2。经过比较，得知路径2 明显优于路径1，所以根据障碍物的大小，改变模糊控制器的模糊论域，能够取得更优路径。

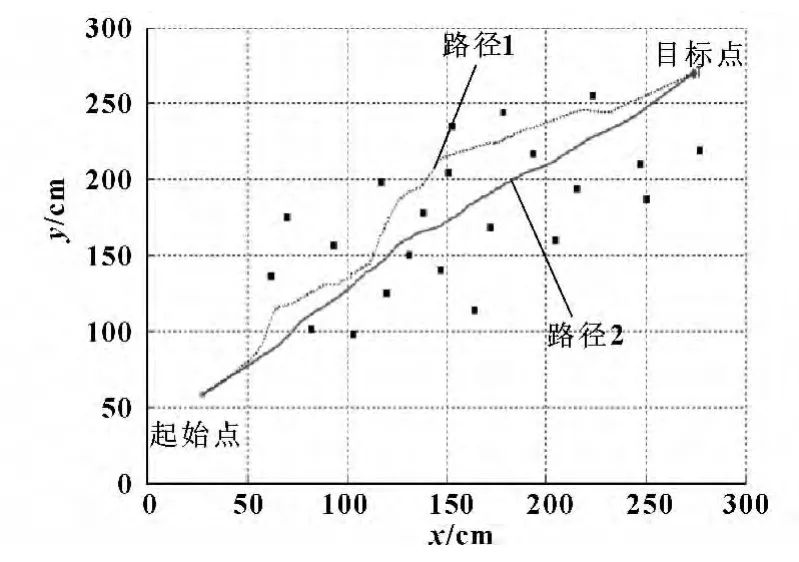
图6 多点障碍物环境中机器人路径规划仿真图

当障碍物较大时，采用模糊控制器2，对应模糊控制表如表2所示，障碍物对水下机器人的最小影响距离为d=100 mm，输入偏转角φ = ［－45°，45°］。首先通过设置多边形，如图中* 号节点连线显示，得到近似转换的矩形，再通过控制器，得到水下机器人的路径。通过设置不同路障的数量、位置、大小，机器人的初始位置、目标点位置等信息，检验了该算法的可行性，仿真结果如图7所示。

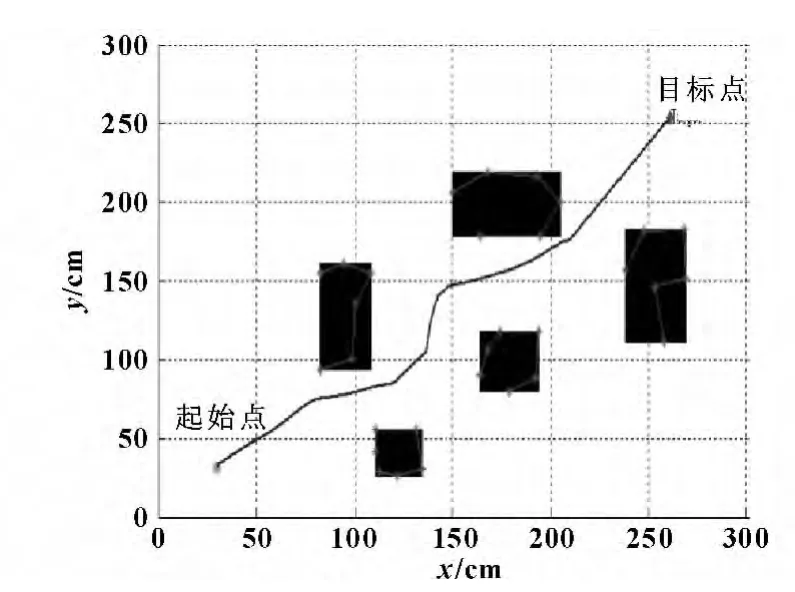
图7 多矩形障碍物环境中机器人路径规划仿真图

4 结论

由于水下机器人运动环境的复杂性、不确定性，机器人难以完全依照预先规划的路径运动。采用测距声呐、短基线系统等传感器，实时探测水下未知环境。基于视线导航原理和模糊控制器，实现了水下机器人的避障路径规划。此外，根据障碍物的不同尺寸，给出了不同的模糊控制器，可获得最优化路径。障碍物不规则时，提取边缘信息后近似转换成矩形障碍物，并讨论了机器人与矩形障碍物处于不同相对位置时相对距离的求取方式。仿真结果表明:该算法对水下机器人在未知环境中对障碍物的数量、形状、大小、位置都没有限制，均可形成一条安全稳定的可靠路径，验证了算法的有效性。

【1】郝宗波，洪炳熔.未知环境下基于传感器的移动机器人路径规划［J］.电子学报，2006，34(5):953－956.

【2】高庆吉，雷亚莉，胡丹丹，等.基于自适应感知复位算法的移动机器人定位［J］.电子学报，2007，35(11):2166－2171.

【3】HUQ R，MANN G K I，GOSINE R G.Mobile Robot Uavigation Using Motor Schema and Fuzzy Context Dependent Behavior Modulation ［J］.Applied Soft Computing，2008，8(1):422－436.

【4】崔荣鑫，徐德民，严卫生.一种自主水下航行器路径规划算法［J］.系统仿真学报，2006，18(12):3373－3376.

【5】陈卫东，朱奇光.基于模糊算法的移动机器人路径规划［J］.电子学报，2011(4):971－974.

【6】李晔，刘建成，徐玉如.带翼水下机器人运动控制的动力学建模［J］.机器人，2005，27(2):128－131.

【7】WU X P，FANG Z P，ZHU J M.Line of Sight Guidance With Intelligent Obstacle Avoidance for Autonomous Underwater Vehicles［C］.OCEANS 2006，Boston，MA，2006:1－6.

【8】李庆春，高军伟，谢广明.基于模糊控制的仿生机器鱼避障算法［J］.兵工自动化，2011，30(12):65－69.

【9】PETILLOT Y，TEMA R I，LAME D M.Underwater Vehicle Obstacle Avoidance and Path Planning Using a Multi-Beam forward Looking Sonar［J］.IEEE Journal of Oceanic Engineering，2001，26(2):240－251.

【10】WANG L X.Adaptive Fuzzy System and Control:Design and Stability Analysis［M］.Englewood Cliffs:PTR Prentice Hall，1994.

【11】谢超平，孔峰，陶金.基于模糊控制的仿生机器鱼转向控制研究［J］.机器人技术与应用，2009(4):26－27.