基于ADAMS的圆锥滚子轴承仿真分析

吕晓菲，山 鹰，王 萌

（1.哈尔滨轴承集团公司 经营发展部，黑龙江 哈尔滨 150036；2.黑龙江东方学院 机电工程学部，黑龙江 哈尔滨150086）

1 前言

圆锥滚子轴承广泛应用于各种机械中，特别是在轨道交通中的关键部位有大量应用，如高速铁路轴箱轴承采用的就是圆锥滚子轴承。圆锥滚子轴承工作载荷特点复杂，为了减少轴承疲劳破坏并优化轴承的动态性能，急需解决其动力学设计和动力学分析等问题。因此借助ADAMS强大的微分方程求解器和图形及数据前、后处理功能，不但可以大大缩短动力学分析所需时间，提高仿真效率，保证分析结果的准确性，而且还具有较高的可靠性[1]。

2 圆锥滚子轴承中的负荷分布

轴承在滚动体中心面同时承受了径向载荷和中心推力载荷，则轴承的内、外套圈将保持平行，并且在轴向和径向分别产生相对位移δa和 δr。以最大载荷滚动体为起点，在任意角度位置ψ 套圈的移动量为

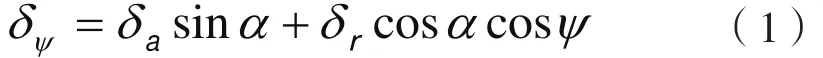
图1 径向和推力载荷联合作用下的轴承位移

图1 是径向和推力载荷联合作用下的轴承位移。当ψ=0°时位移达到最大，并由下式给出

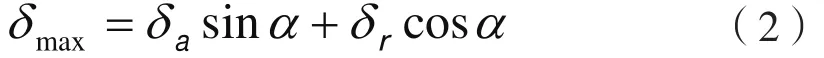
合并式（1）和式（2），得

式中，

显然还有

为了保持静力平衡，在各个方向上滚动体受力之和必须等于该方向上的作用载荷

式中，载荷角定义为

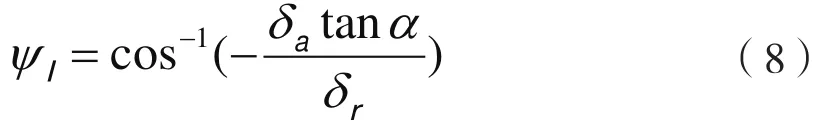
式（6）和式（7）可以分别写成径向积分和推力积分的形式：

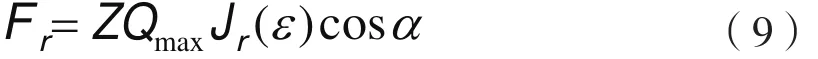
式中

式中

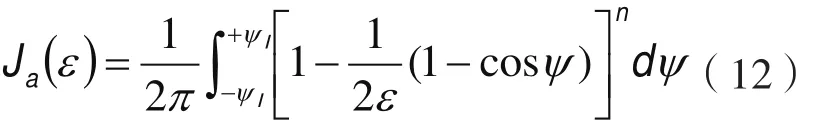
值得指出的是，对所有受力中的球或滚子接触角假定是不变的，因此积分值就是近似的。但对于大多数计算，这些积分值还是具有足够的精度。利用这些积分，得

3 模型的导入

利用三维造型软件PRO/E，对圆锥滚子轴承进行建模，将圆锥滚子轴承的PRO/E模型另存为ADAMS可以识别的格式，打开ADAMS/View将其导入。导入模型后，设置系统单位、重力加速度，然后将内圈、外圈、保持架分别命名，其余保持默认。材料定义为steel。

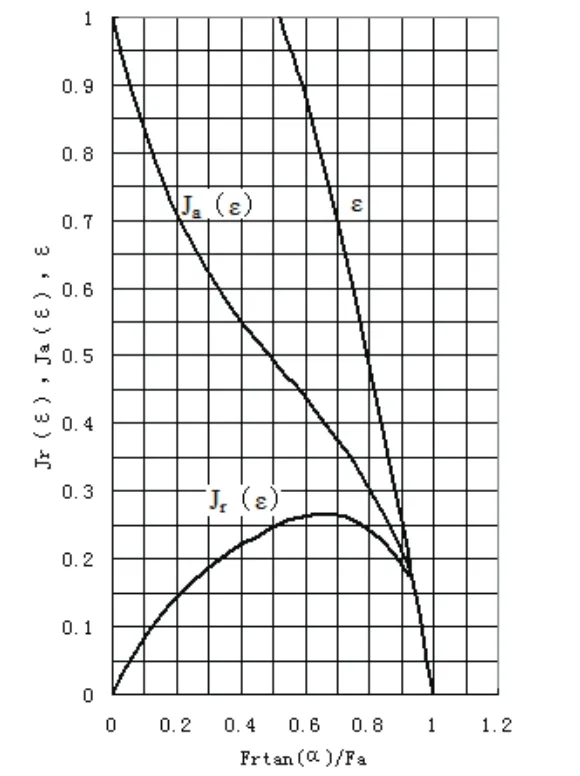
图2 线接触轴承J r、J a和ε与tanα/F a的关系

4 添加约束及载荷

一个系统通常是由多个构件组成的，各个构件之间通常存在某些约束关系，即一个构件限制另一个构件的运动。ADAMS/View中就是通过为各个构件之间添加不同的约束关系来模拟现实中的运动关系的。滚子与套圈、保持架之间添加接触约束，外圈固定，内圈旋转，轴承内圈同时施加径向载荷与轴向载荷，模拟轴承实际运作工况条件。

5 ADAMS碰撞力的定义

在ADAMS 中有两种定义碰撞力的方法：一种是补偿法（Restitution）；另一种是冲击函数法（Impact）。相对而言，前者的参数更难准确设置，所以本文选用冲击函数法来计算碰撞力。冲击函数法是根据impact 函数来计算两个构件之间的碰撞力，碰撞力由两个部分组成：一个是由于两个构件之间的相互切入而产生的弹性力；另一个是由于相对速度产生的阻尼力。

impact 函数的一般表达式为：

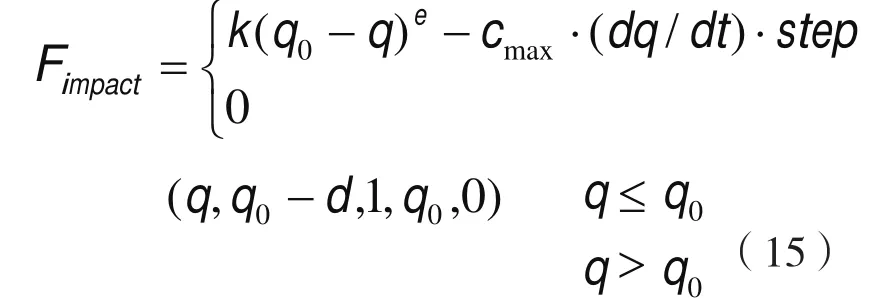
式中：qo为两个要碰撞物体的初始距离；q为两物体碰撞过程中的实际距离；dq / dt为两个物体间距离随时间的变化率，即速度；k为刚度系数；e为碰撞指数；Cmax为最大阻尼系数； d为切入深度，它决定了何时阻尼力达到最大；为了防止碰撞过程中阻尼力的不连续，式中采用了step 函数，其形式为step（χ，χ0，h0，χ1，h1），按式（16）进行计算[3]。

6 碰撞参数设置分析

从ADAMS 碰撞力定义的分析表明，碰撞接触力仿真需要确定刚度系数、碰撞指数、阻尼系数和阻尼系数达到最大所要经过的距离d 。但如果想得到比较精确的结果，就需要对这些参数进行准确的分析设置[4]。

（1）对旋转物体的碰撞，其刚度系数可近似地根据下式来确定[5]：

对于非旋转体的碰撞，刚度系数采用ADAMS默认值进行计算。

（2）由式(1)可知，碰撞指数e 反映了材料的非线性程度。其推荐值：金属与金属材料为1.5；橡胶材料为2。

（3）最大阻尼系数Cmax表征碰撞能量的损失。其值通常设为刚度系数的0.1～1%。

（4）切入深度表征最大阻尼时的侵入深度。刚碰撞时，没有阻尼力，随着侵入深度增大，阻尼力加大，直到最大阻尼力。其适合值为0.1mm。

7 仿真分析

轴承承受径向载荷Fr=60 758 N，轴向载荷Fa=30 260N，转速n=2 000 r/min。对轴承仿真模拟时间1.5 s，利用ADAMS后处理模块可以得到滚子与内圈、滚子与外圈以及滚子与保持架之间的碰撞力。图3 是圆锥滚子轴承的ADAMS动力学仿真模型。

图4 是红色滚子在不同位置与外圈的碰撞力的变化曲线，从图中同样可以看出滚子公转一周所受的载荷是不断变化的。滚子所受载荷方向与径向加载方向相同时，滚子所受载荷为最大，理论值Q理max=15652N，仿真值Q仿max=15098N，相对误差约为4%；与径向加载方向相反时，滚子所受载荷最小，理论值Q理max=13721N，仿真值 Q仿max=3485N，相对误差不超过7%。图5 是滚子不同位置载荷分布理论曲线图。可以看出仿真效果比较准确。

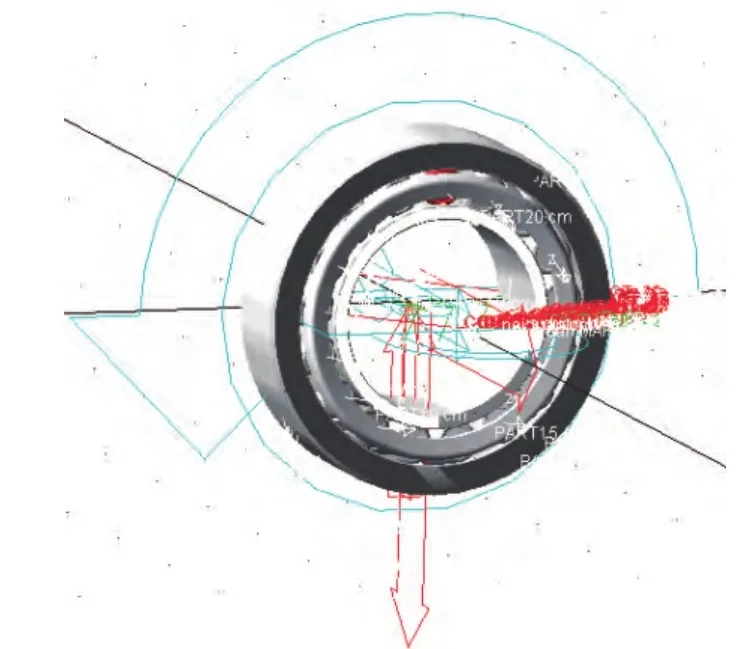
图3 圆锥滚子轴承的ADAMS动力学仿真模型

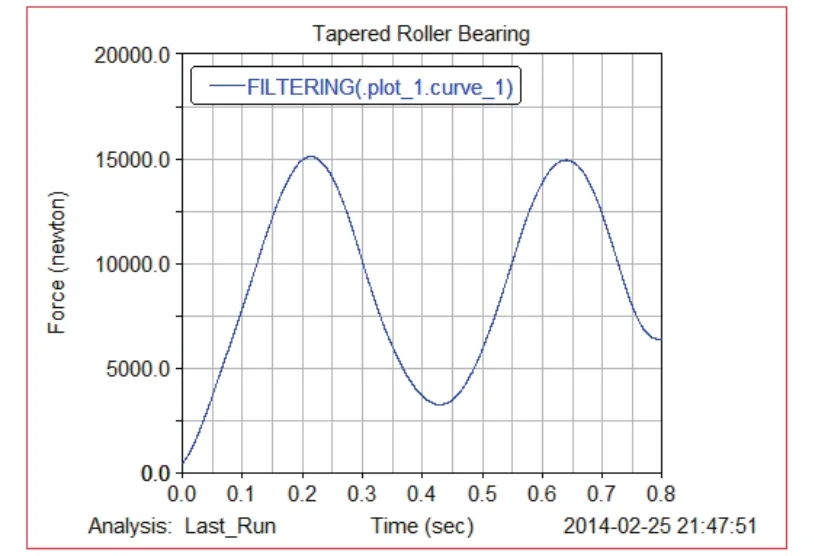
图4 滚子不同位置载荷分布图

图5 滚子不同位置载荷分布图

8 结束语

采用动力学仿真软件ADAMS对圆锥滚子轴承进行仿真分析，该方法基于碰撞模型，通过计算确定各相关参数，然后应用impact函数，求解滚子与内圈、外圈、保持架之间的碰撞力，研究圆锥滚子轴承滚子载荷分布，准确模拟了轴承动力学特性，为轴承动态设计提供理论依据，缩短产品研发周期。

[1] 谢最伟，吴新跃.基于ADAMS 的碰撞仿真分析[M].第三届中国CAE 工程分析技术年会论文集，2007.

[2] T.A.Harris.滚动轴承分析[M].北京：机械工业出版社，2010.

[3] 朱利军，谭晶，黄迪山，徐洋，傅慧燕.基于ADAMS的深沟球轴承仿真分析[J].轴承，2011, (2).

[4] 张风琴，杜辉，邓四二，杨海生，高银涛.基于ADAMS的圆柱滚子轴承仿真分析[J].河南科技大学学报：自然科学版，2009.

[5] 龙凯，程颖.齿轮啮合力仿真计算的参数选取研究[J].计算机仿真，2002，19(6)：87～88，91.

[6] 石明全.基于ADAMS 的多接触研究[J].计算机工程与应用，2004，（29）：220～222.