Responses of Longitudinal and Transversal Nonlinear Coupling Vibration of Ship Shafting

YANG Zhi-rong,ZOU Dong-lin,RAO Zhu-shi,Ta Na

(1 State Key Laboratory of Mechanical System and Vibration,Shanghai Jiao Tong University,Shanghai 200240,China;2 Marine Engineering Institute,Jimei University,Xiamen 361021,China)

1 Introduction

When ship sailing on the water,it inevitably brings non-uniform wake field in the stern.Propeller works in spatially non-uniform wake field would produce plus forces which transfer to the hull through the propulsion shaft and the thrust bearing and its base.The plus forces may cause shafting vibration that propagates through the supporting structure to the hull,and results in a high-level structure-borne noise[1-3].The vibration transmission through the propellershafting system of ships and submarines represents a critical issue that must be addressed in order to reduce the acoustic signature.Transversal centrifugal forces produced from the concentrated mass and the coupler due to shaft rotation,which are another transversal vibration excitation sources.The amplitude of the generated vibration response is small if the amplitude of the excitation force is small and the coupling effect between longitudinal and transversal vibrations is weak,therefore the vibrations of the whole shafting system are linear.The linear shafting vibration calculation methods can be used such as:analytical method,Holzer method,Tolle law,Tepckux law,energy law,amplification factor method and transfer matrix method etc.In addition,some researchers[4-5]analyzed,corrected,improved the linear shafting vibration calculation methods,and proposed a variety of new algorithms.

The doubly coupled transversal-torsional vibrations of monosymmetric beams and the doubly coupled longitudinal-torsional vibrations of monosymmetric beams have been investigated by several authors.Li[6]analyzed the coupled transversal and torsional vibration of axially loaded Bernoulli-Euler beams taking into account the effect of warping stiffness and gave allowance to the presence of axial force.Vörös[7]presented a numerical method to analyze the effect of steady state lateral loads on the coupled transversal-torsional vibrations and mode shapes of Bernoulli-Vlasov beams.He found that the initial bending moment had a significant effect on the mode shapes which proved the need of second order dynamics in structural analysis.Klausbruckner[8]studied on coupled vibration of thin-walled channel beams with different cross-sectional areas and lengths,which were conducted using theoretical and experimental approaches.The theoretical approach was based on analytical and finite element methods and the experimental approach utilized the methods of laser hologram interferometer.Al-Bedoor[9]developed a model for the coupled torsional and transversal vibrations of unbalanced rotors,which treated the rotor torsional deformation angle as an individual degree of freedom.Simulation results showed energetic interaction between the rotor transversal and torsional vibrations.Chen[10]investigated the coupled axial-torsional vibration of thin-walled Z-section beam induced by boundary conditions,otherwise the effect of boundary conditions and the value of warping function at centroid on the coupled axial and torsional natural frequency of Z-section beam was also studied.However,the doubly coupled transversal-longitudinal vibrations of monosymmetric beams or shafts with multi-elastic supports have been little reported in the recent literature.

The relatively large deflection deformation of the shafting is produced if the excitation force is large,thus its elastic coupling effect of longitude and transverse becomes notable and affects the shafting vibration.It is necessary to study the responses of longitudinal and transversal coupling nonlinear vibrations of ship shafting.Such solving methods of the nonlinear problem are usually as:Galerkin/Newton-Raphson method(N/R),the harmonic balance method,the perturbation method,the incremental harmonic balance method and numerical integration method.Incremental harmonic balance method(IHB)[11]firstly spreads the differential equations of motion by NR method,then solves incremental differential equations in the frequency domain.Analytical solutions of simple structures with simple boundary conditions can be well obtained and have certain guiding significance to the engineering practice application.However,the propulsion shaft which has multi-elastic supports and lumped mass,it has some difficulty in seeking the solutions of the equations just utilizing the analytical method such as the Incremental Harmonic Balance method.The FEM has advantages in modeling simply and good processing in the complex structures with complex boundary conditions.Therefore,it gradually becomes the main method for calculating practical engineering problems.Hu[12]utilized the FEM to derive the longitudinal and transversal coupled nonlinear beam element stiffness matrix and proposed using iterative method to solve the nonlinear problems.However,the investigated structure is relatively simple and the results can not reveal some important characteristics of the actual structure.In this paper,the ship shafting with multi-elastic supports and lumped mass is studied.The FEM is used to establish the dynamic model of the longitudinal and transversal coupling vibration.The responses of linear vibration and nonlinear coupling vibration of propulsion shaft are calculated and the results are analyzed.The results have certain guidance significance to the practical engineering research for ship shafting.

2 The governing differential equations of coupling vibration

The beam structure model is used to simplify the propulsion shaft shown in Fig.1.It suffers the longitudinal and transversal harmonic loads.Here the shear,the moment of inertia,and the fluctuation effect of propulsion shaft are neglected.Considering u to o),the partial differential equations of coupling vibration for shaft can be written as follows[13]:

Fig.1 The model of beam structure

The ship shafting mainly consists of the propeller,propeller shaft,intermediate shaft,flange,thrust shaft,thrust bearing and its base.Here the propeller and its attached waterare simplified as lumped mass M,furthermore the propulsion shaft is equivalent to a distributed mass and flexibility homogeneous shaft.Radial stiffness of stern bearing and intermediate bearing is equivalent to linear spring stiffness.Radial and longitudinal stiffness of thrust bearing and its base is also equivalent to linear spring stiffness.It usually can be simplified as shown in Fig.2.

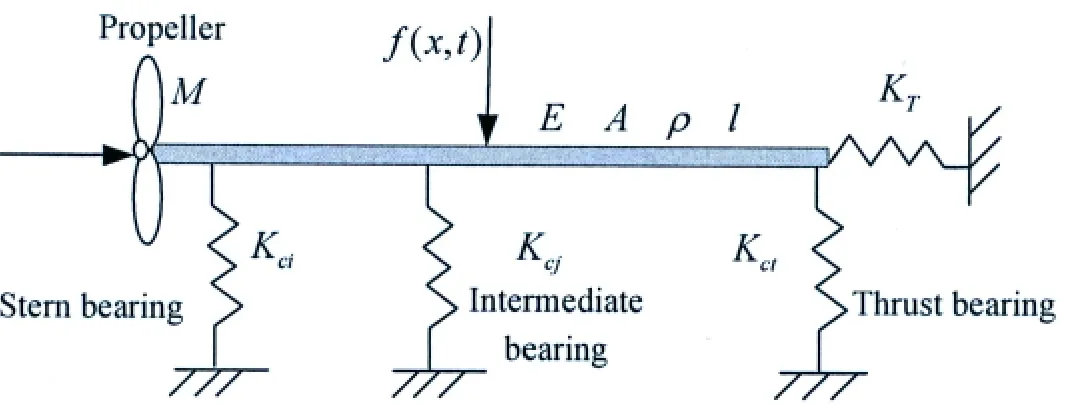
Fig.2 The ship shafting with multi-elastic supports and lumped mass

3 Finite element modeling of nonlinear coupling vibration of ship shafting

3.1 The stiffness and mass matrix of the beam element

The plane beam element is used to simulate the longitudinal vibration and the transversal vibration of ship shafting.A two-node beam element is shown in Fig.3.The length of the beam element is L.Each node has three degrees of freedom,which are the displacements of longitudinal,transversal and rotation,respectively.The node vector of the element can be written as[14]:

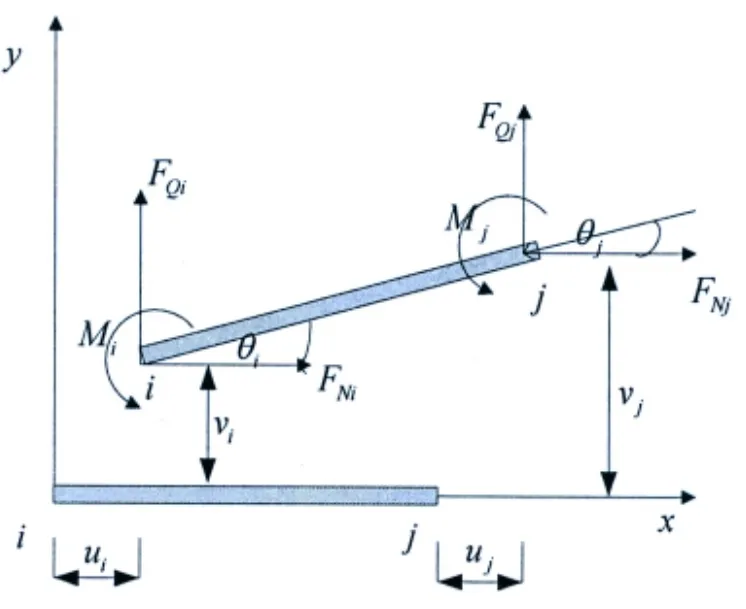
Fig.3 The beam element

A linear interpolation function is used to denote the longitudinal displacement of the element and the cubic polynomial function is used to denote the transversal displacement of the element as follows:

Considering the coupling interaction,the potential energy and kinetic energy of the beam element can be expressed as:

Substituting the expression(3)into the Eq.(8),the stiffness matrix of the beam element is composed of the following three parts[12]:

Substituting the expression(3)into the Eq.(8),the mass matrix of the beam element can be obtained as:

3.2 The stiffness and mass matrix of the beam element with multi-elastic supports and lumped mass

If the beam element has radial elastic supports Kciand Kcjat the left and right nodes respectively,furthermore has a longitudinal elastic support KTat the right node as shown in Fig.4,its linear stiffness matrix can be written as[15]:

Fig.4 The beam element with-elastic supports and lumped mass

If there is lumped mass Miat the left node i and lumped mass Mjat the right node j,the mass matrix of the element is:

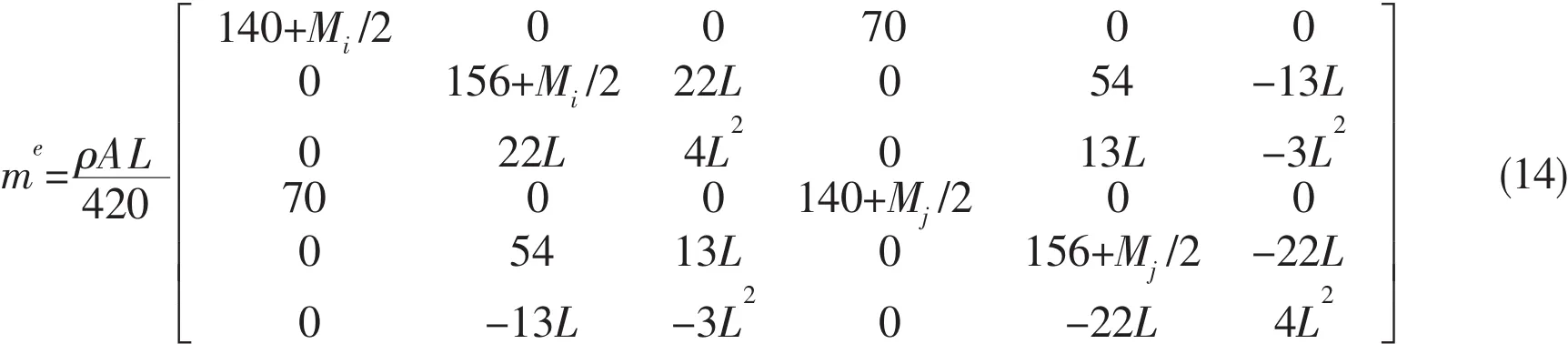
If there is a static force acting on the element,the additional element stiffness matrix generated by the axial force is:

4 Example and results

The length of propulsion shaft is 14.46 m.It has an outside diameter of 280 mm and an inside diameter of 165 mm,respectively.The mass of the propeller and added water is 6 875 kg,and the mass of couplings follower end is 1 300 kg.The shafting system has Young’s modulus of 214 GPa and density of 7 850 kg/m3,respectively.The radial stiffness of stern bearing is 3.05×108N/m and the radial stiffness of intermediate bearing is 1.06×108N/m.The radial stiffness of thrust bearing is 2.66×108N/m and the longitudinal stiffness of thrust bearing is 1.342 5×1010N/m.The shafting system suffers a static axial force,which is P=19 600 N.It is in a static equilibrium state in initial time.Apply the left end of shaft with longitudinal harmonic excitation force,its amplitude is FL=5.86×105N and its frequency is fL=23.3 Hz.Apply the middle position of shaft with transversal harmonic excitation force,its amplitude is FT=3×105N and its frequency is fT=20 Hz.Considering the influence of damping,we set ξ=0.01.The nonlinear vibration responses of the propulsion shaft are calculated by using the combination of the Newmark method and the Newton-Raphson method.

4.1 The natural frequencies of ship shafting affected by the axial force

When the propulsion shaft works under the sea water,the axial force can be produced from static thrust.The natural frequencies of ship shafting are affected by the axial force as well as the structure dimension parameters of ship shafting.Tab.1 shows the impact of the natural frequencies of ship shafting affected by different axial forces.

Tab.1 The natural frequencies of ship shafting affected by different axial forces

Seen from Tab.1,the natural frequency of ship shafting in each order is slightly reduced as the axial force increasing.This can be explained by the formula(15),in which the stiffness of the element is slightly reduced as the axial force increasing.Thus,the natural frequencies of ship shafting are also slightly reduced,however the impact is little.

4.2 The responses of nonlinear coupling vibration of ship shafting

Fig.5 shows the displacement curves of longitudinal vibration of ship shafting in time and frequency domains considering the coupling vibration effect.The figure shows the maximum displacement amplitude of the longitudinal vibration is approximately 1.04 mm.When the longitudinal and transversal coupling vibration effect is taken into account,one peak response frequency is corresponding to the excitation frequency of the linear longitudinal vibration at 23.3 Hz.In addition,the frequency in the low fre-quency region,the frequencies 40 Hz in the inter-mediate frequency region,and the frequency 80 Hz(4fT)also have peak responses due to the coupling effect.Fig.6 shows the displacement curves of transversal vibration of ship shafting in time and frequency domains considering the coupling vibration effect.The figure shows the maximum displacement amplitude of the transversal vibration is approximately 11 mm.When the longitudinal and transversal coupling vibration effect is taken into account,one peak response frequency is corresponding to the excitation frequency of the linear transversal vibration at 20 Hz.In addition,the frequencies 3.3and 60 Hz(3fT)also have peak responses due to the coupling effect.

Fig.5 The displacement time-history and amplitudefrequency curves of nonlinear coupling longitudinal vibration of ship shafting

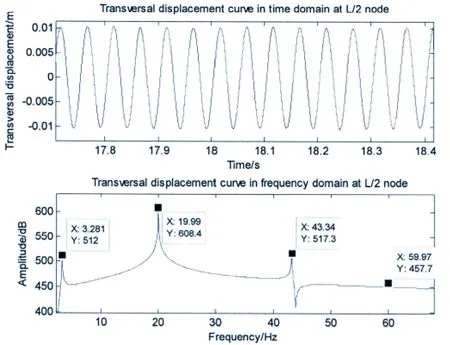
Fig.6 The displacement time-history and amplitude-frequency curves of nonlinear coupling transversal vibration of ship shafting

Fig.7 Comparison of time-history responses between linear and nonlinear longitudinal vibrations

Figs.7-8 are the comparison of linear and nonlinear longitudinal vibration responses in time and frequency domains.We can see from Fig.7 that the displacement responses of nonlinear longitudinal vibration with coupling effect are larger than the responses of linear longitudinal vibration.The results are due to coupling excitation items.Seen from Fig.8,the longitudinal vibration responses with and without coupling effect have a common excitation frequency component at 23.3 Hz.In addition,the coupling vibration responses have frequency components with transversal excitation frequency doubling and excitation frequenciesof addition or subtraction and other linear combinations.

Fig.8 Comparison of amplitude-frequency responses between linear and nonlinear longitudinal vibrations

Figs.9-10 are the comparison of linear and nonlinear transversal vibration responses in time and frequency domains.We can see from Fig.9,the displacement responses of transversal vibration with and without coupling effect are basically the same.This may because the coupling excitation effect is not obvious,so the response amplitude of coupling vibration is small and almost the same to the response amplitude of linear vibration.However,seen from Fig.10,the coupling vibration responseshave frequency components with excitation frequencies of addition or subtraction linear combinations as well as the common excitation frequency component of the transversal vibration.

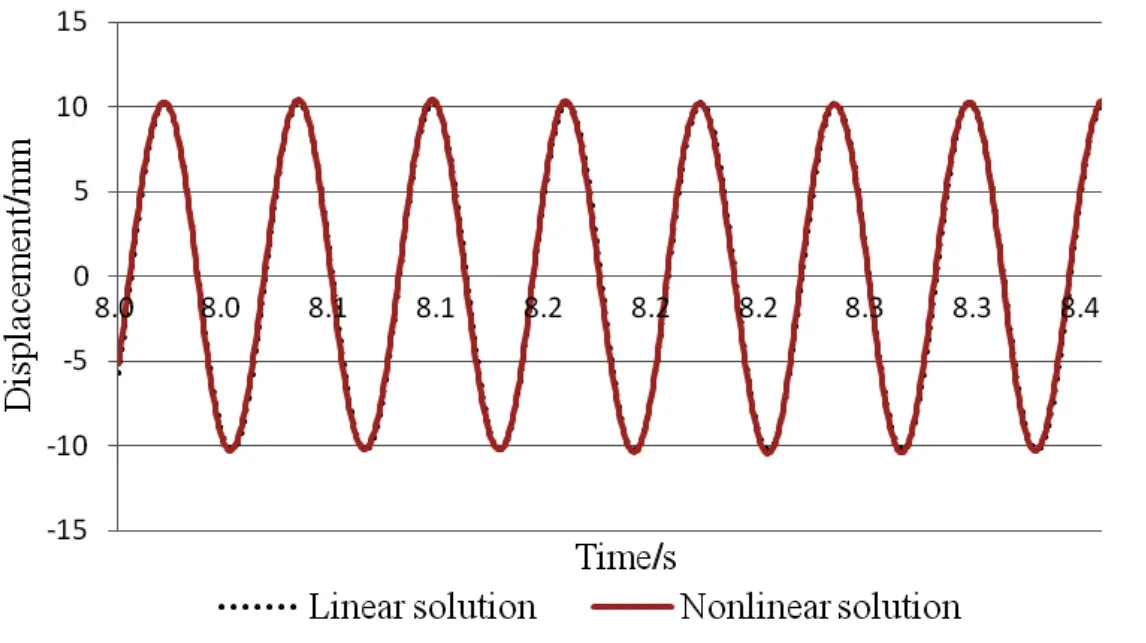
Fig.9 Comparison of time-history responses between linear and nonlinear transversal vibrations

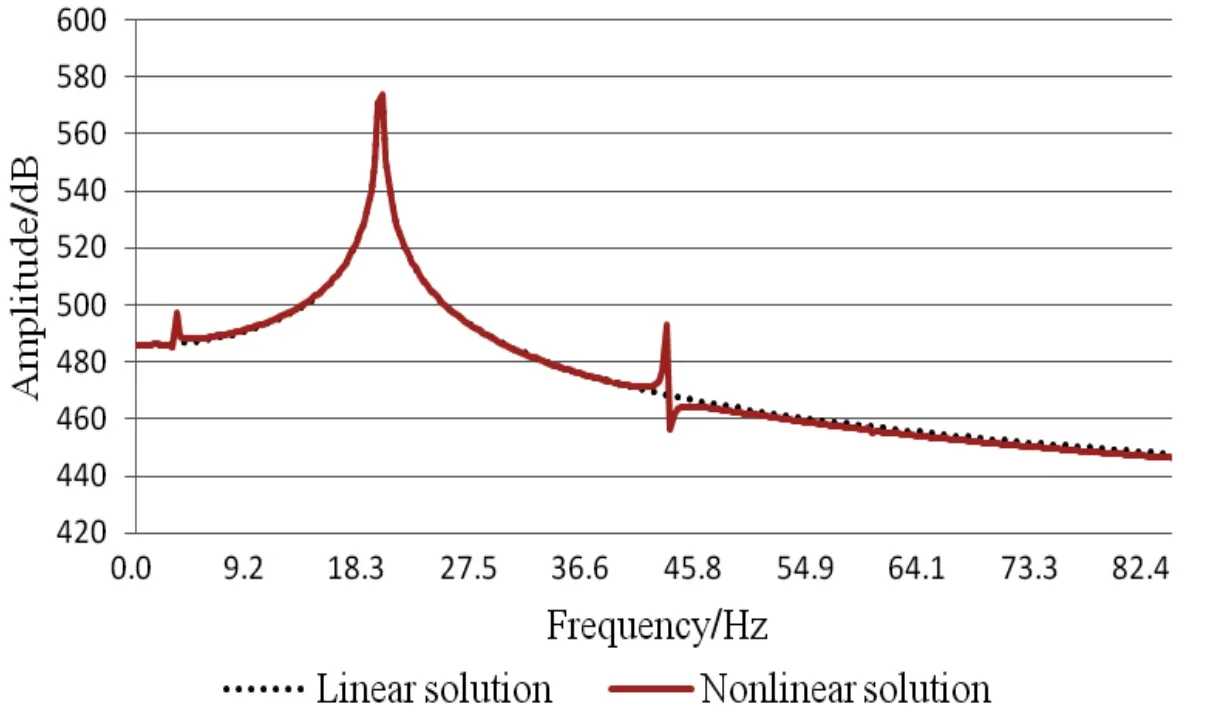
Fig.10 Comparison of amplitude-frequency responses between linear and nonlinear transversal vibrations

In general,the time-history responses of coupling vibration are larger than linear vibration responses,especially in the longitudinal vibration.Furthermore,there are many frequency components in the frequency domain.Therefore,if there is coupling effect in the system,the natural frequencies of design system not only should avoid the excitation frequencies but also should avoid the combined excitation frequencies.

5 The law of the responses of nonlinear coupling vibration with different excitation force amplitudes

In order to investigate the impact of different excitation force amplitudes effect on the responses of nonlinear coupling vibration,different amplitude combinations of longitudinal and transversal excitation forces applied to the shaft are divided into three groups as follows:A.FL=8×103N,FT=5×102N;B.FL=8×103N,FT=5×104N;C.FL=8×104N,FT=5×102N.The frequencies of longitudinal and transversal excitation forces remain fL=23.3 Hz and fT=20 Hz unchanged.Other parameters and conditions are the same as mentioned above in the example.The displacement time-history and amplitude-frequency curves of nonlinear coupling vibration of ship shafting while applying with different excitation force amplitudes are shown in the Figs.11-13.

Fig.11 The displacement time-history and amplitude-frequency curves of nonlinear coupling vibration of ship shafting(while FL=8×103N,FT=5×102N)

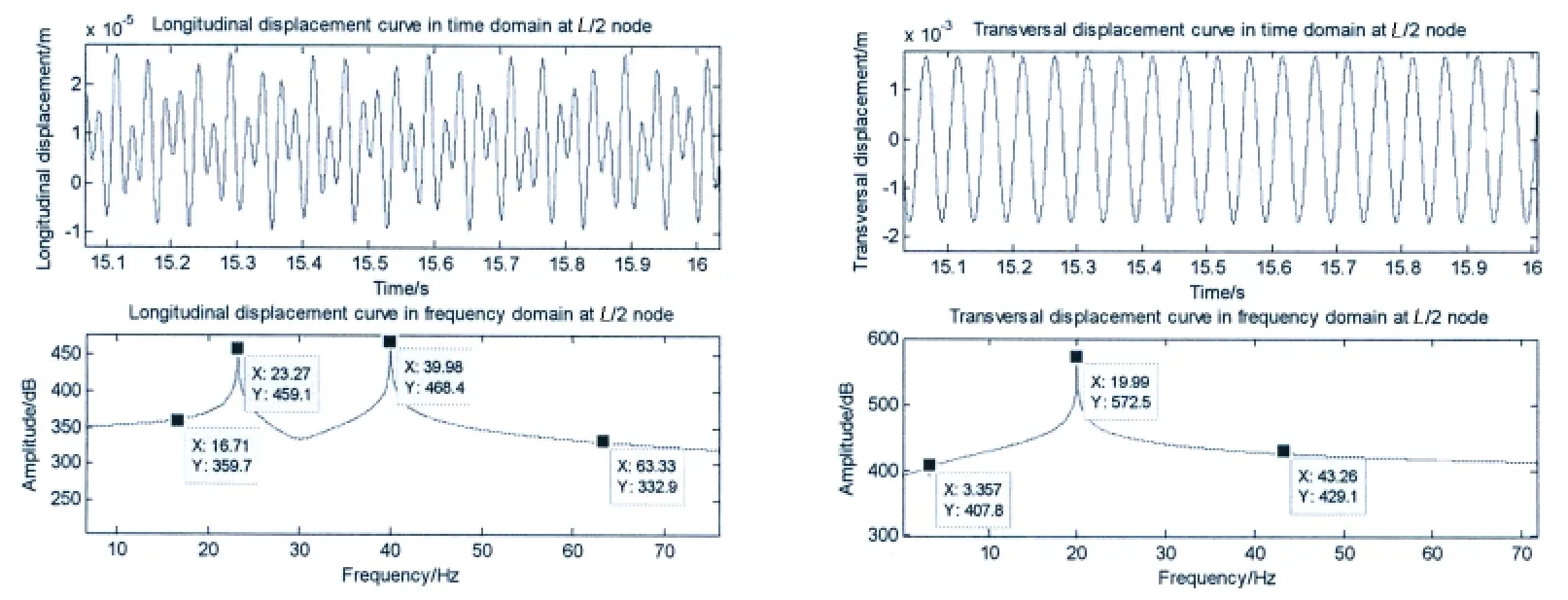
Fig.12 The displacement time-history and amplitude-frequency curves of nonlinear coupling vibration of ship shafting(while FL=8×103N,FT=5×104N)

By comparing Fig.11 and Fig.12,which the system is applied with the excitation loads of group A and group B respectively,we can see that the longitudinal vibration nonlinear effect is significantly enhanced as the transversal excitation force amplitudes increasing.

By comparing Fig.11 and Fig.13,which the system is applied with the excitation loads of group A and group C respectively,we can see that there is a certain increase in the responses of transversal nonlinear vibration as the longitudinal excitation force amplitudes increasing.The Fig.13 shows that the longitudinal vibration nonlinear effect is little because the transversal excitation force amplitude is small.Comparing Fig.12 and Fig.13,we can see that the transversal force impacts on the nonlinear coupling effect of longitudinal vibration is more significant than the longitudinal force impacts on the nonlinear coupling effect of transversal vibration.

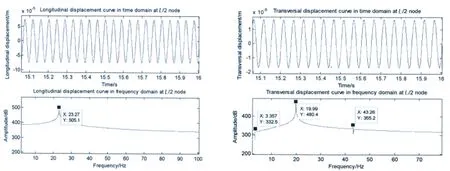
Fig.13 The displacement time-history and amplitude-frequency curves of nonlinear coupling vibration of ship shafting(while FL=8×104N,FT=5×102N)

6 The law of the responses of nonlinear coupling vibration under different excitation frequencies

In order to investigate the impact of different excitation frequencies effect on the responses of nonlinear coupling vibration,different excitation frequency combinations are divided into two groups based on the closeness between fLand fTas follows:D.fL=23.3 Hz,fT=3.3 Hz;E.fL=23.3 Hz,fT=20 Hz.The amplitudes of longitudinal and transversal excitation forces remain FL=8×103N and FT=5×103N unchanged.Other parameters and conditions are also the same as mentioned above in the example.The displacement time-history and amplitude-frequency curves of nonlinear coupling vibration of ship shafting while applying with different excitation frequencies are shown in the Figs.14-15.

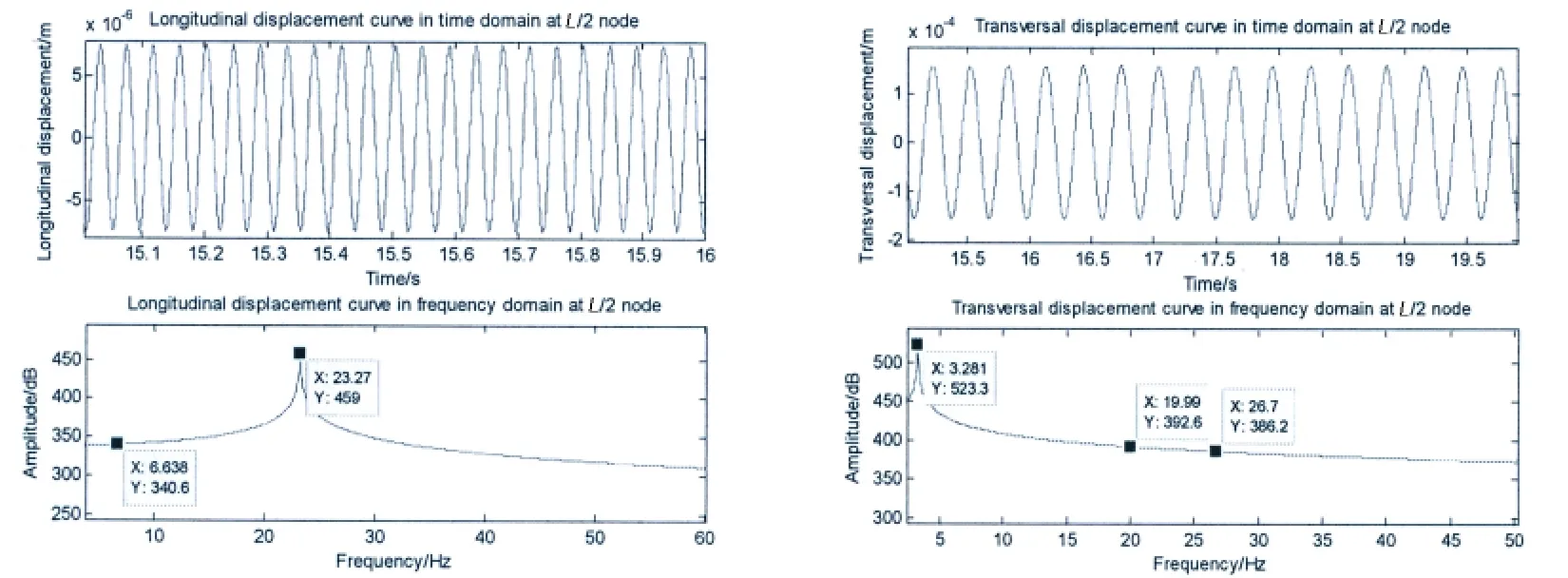
Fig.14 The displacement time-history and amplitude-frequency curves of nonlinear coupling vibration of ship shafting(while fL=23.3 Hz,fT=3.3 Hz)

By comparing Fig.14 and Fig.15,which the system is applied with the excitation frequen-cies of group D and group E respectively,we can see that the closer between fLand fTthe more significant of nonlinear coupling effect between longitudinal and transversal vibrations.

Fig.15 The displacement time-history and amplitude-frequency curves of nonlinear coupling longitudinal vibration of ship shafting(while fL=23.3 Hz,fT=20 Hz)

7 Conclusions and discussion

Ship shafting with multi-elastic supports and lumped mass is studied in this paper by the FEM based on the nonlinear stiffness and mass matrix of the beam element.Responses of longitudinal and transversal coupling vibration are calculated with different excitation force amplitudes and different excitation frequencies,furthermore the results are analyzed.Based on the results obtained in this study,the following conclusions can be drawn:

(1)When the amplitude of shaft vibration is relatively large,the phenomenon of combined harmonic peak responses of the system is easily produced due to longitudinal and transverse nonlinear coupling effect.The system has many peak frequencies in responses.

(2)Extensive analysis results show that the combined harmonic response components mainly distributeor 2fTin longitudinal vibration andin transversal vibration due to the longitudinal and transverse nonlinear coupling forced vibration.

(3)The larger amplitudes of excitation forces,the stronger of coupling effect in the nonlinear vibration.In addition,the transversal force impacts on the nonlinear coupling effect of longitudinal vibration is more significant than the longitudinal force impacts on the nonlinear coupling effect of transversal vibration.

(4)The closer between fLand fTin the excitation frequencies,the more significant nonlinear coupling effect between longitudinal and transversal vibrations.

(5)If there is a peak frequency component in the responses of the system,maybe caused by the same frequency of the excitation source,also maybe the combined frequency of different excitation sources which is equal to the peak frequency.Therefore appropriate measures should be taken to against the relevant excitation sources for effective control.They will be helpful to completely eliminate the peak response components or to reduce the response amplitudes.By the way,increasing the damping of shafting system is also helpful for reducing the responses of nonlinear coupling vibration in longitudinal and transversal direction,respectively.

[1]Dylejko P,Kessissoglou N,Tso Y,et al.Optimisation of a resonance changer to minimise the vibration transmission in marine vessels[J].Journal of Sound and Vibration,2007,300(1-2),101-116.

[2]Pan X,Tso Y,Juniper R.Active control of radiated pressure of a submarine hull[J].Journal of Sound and Vibration 2008,311(1-2):224-242.

[3]Xie J R,S S,Wu Y S.Research status on noise radiation from vibrating hull induced by propeller and reduction measures[J].Shipbuilding of China,2010,51(004):234-241.

[4]Chen X.Ship shafting torsional vibration calculation and analysis of test cases[J].Ship Engineering,2002,(001):22-26.

[5]Wang Z.Improved transfer matrix method for torsional vibration analysis[J].Journal of North China Electric Power University,2001,28(003):17-27.

[6]Jun L,Rongying S,Hongxing H,et al.Coupled bending and torsional vibration of axially loaded Bernoulli-Euler beams including warping effects[J].Applied Acoustics,2004,65(2):153-170.

[7]Vörös G M.On coupled bending-torsional vibrations of beams with initial loads[J].Mechanics Research Communications,2009,36(5):603-611.

[8]Klausbruckner M,Pryputniewicz R.Theoretical and experimental study of coupled vibrations of channel beams[J].Journal of Sound and Vibration,1995,183(2):239-252.

[9]Al-Bedoor B.Modeling the coupled torsional and lateral vibrations of unbalanced rotors[J].Computer Methods in Applied Mechanics and Engineering,2001,190(45):5999-6008.

[10]Chen H H,Hsiao K M.Coupled axial-torsional vibration of thin-walled Z-section beam induced by boundary conditions[J].Thin-walled Structures,2007,45(6):573-583.

[11]Xia P.Harmonic responses of beams with longitudinal and transversal coupling[J].Journal of Vibration Engineering,1995,8(001):67-72.

[12]Hu Yi,Y J.Studies on the longitudinal and lateral coupled vibration of beam[J].Journal of Wuhan University of Technology:Transportation Science&Engineering,2010,34(003):537-541.

[13]Nayfeh A H,Mook D T.Nonlinear oscillations[M].Wiley-VCH,2008.

[14]Xu R.Structural analysis of the finite element method and MATLAB programming design[M].Beijing:China Communications Press,2006.

[15]Zhang Z.Numerical calculation of power equipment vibration[M].Harbin:Harbin Engineering University Press,2007.