Weakly Compressible Moving Particle Semi-Implicit Method(WC-MPS)with Large-Eddy Simulation(LES)Turbulence Model for Numerical Simulation of Dam-break Flows

LIU Yong-tao,MA Ning,ZHU Ren-qing,GU Xie-chong

(1 School of Naval Architect,Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;2 School of Naval Architect and Ocean Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003,China)

1 Introduction

Moving Particle Semi-implicit(MPS)method was firstly presented by Koshizuka[1-2]and then increasingly became a powerful approach for the numerical simulation of the fluid flow with violent free surface profiles,such as dam-break[3-5],wave breaking[6-7],wave-body interaction[8],green water[9-10],and tank sloshing[11-12].Up to now,many researchers have carried out series of useful studies to improve this method.For example,Yoon et al[13]proposed an Eulerian-Lagrangian hybrid MPS method named MPS-MAFL(Meshless Advection using Flow directional Local grid)to model the convection terms in the momentum equations.Gotoh et al[14]implemented MPS method with the sub-particle-scale(SPS)turbulence model for fluid flow with high Reynolds number.Because the phenomenon of unphysical pressure fluctuation is a major disadvantage of the MPS method,so it has been improved by modifying the calculation scheme of the pressure-gradient terms by Khayyer and Gotoh[15]by proposing a new incompressible condition,and Shakibaeinia and Jin[3]by representing a weakly compressible MPS method(WC-MPS)to compute the fluid pressure by the equation of the state of the fluid,and so on.In this paper,a weakly compressible MPS method implemented with a Large-Eddy Simulation(LES)turbulence model is introduced and used to study two 2-D dam-break problems involving violent free surface flows.

2 Governing equations for fluid flow problem

2.1 Governing equations

For weakly compressible and viscous fluid flow problem,governing equations are as follows:

where,t is time,ulis fluid velocity,ρ is fluid density,p is fluid pressure,Fblis body force,ν0is laminar kinematic viscosity of the viscous fluid,νtis turbulence eddy viscosity of the viscous fluid,Slmis angular deformation rate,l and m are the number of the direction.

2.2 Turbulence model

To effectively simulate the violent viscous flow,the Large Eddy Simulation(LES)Smagorinsky turbulence model[14]is applied to compute the sub-particle-scale(SPS)turbulent terms.In Eq.(2),the turbulence eddy viscosity νtis obtained by:

where,l0is particle distance,Csis the Smagorinsky constant which is within 0.1～0.2,andis local strain rate can be determined as follows:

3 WC-MPS method

3.1 Kernel function

For the WC-MPS method,the flow field is represented by a large quantities of the fluid particles possessing physical quantities such as velocity and pressure.With the numerical simulation continuing,these fluid particles will move round and interact with their neighbors,re-sulting in exchanging of their physical quantities.In order to describe the interacting discipline between these particles,the kernel function w(r)is defined and limited to the region called effective radius.And here,a kernel function is used as follows[3]:

where,reis effective radius,and re=3.2l0,l0being particle distance.

3.2 Particle number density

To describe the changes of the fluid density caused by the particle motion,the particle number density niis introduced to define the intensity of the fluid particles within effective radius of particle i.Therefore,for particle i located at ri,particle number density niwill be as follows:

where,rjis the real time position of the particle j,and symbol〈〉 is kernel smooth operator.

3.3 WC-MPS Gradient model

The gradient terms in the governing equations are obtained by the weighted averaging of the gradient vector.Here we consider a scalar quantity φ,its gradient vector at the particle i can be calculated by its neighbors j within the effective radius as follows:

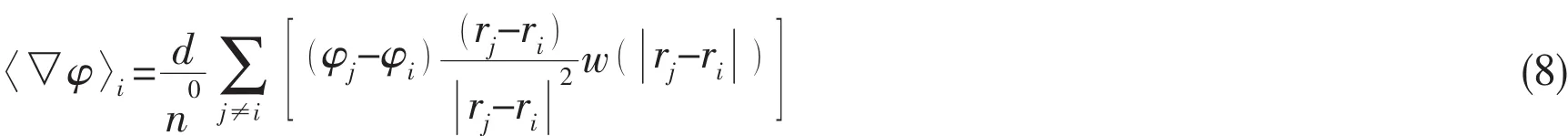
where d is the space dimensions of the fluid domain,and n0is initial particle number density.

3.4 WC-MPS Laplacian model

For Laplacian terms in the momentum equation,the applied model is based on the following formula[1]:

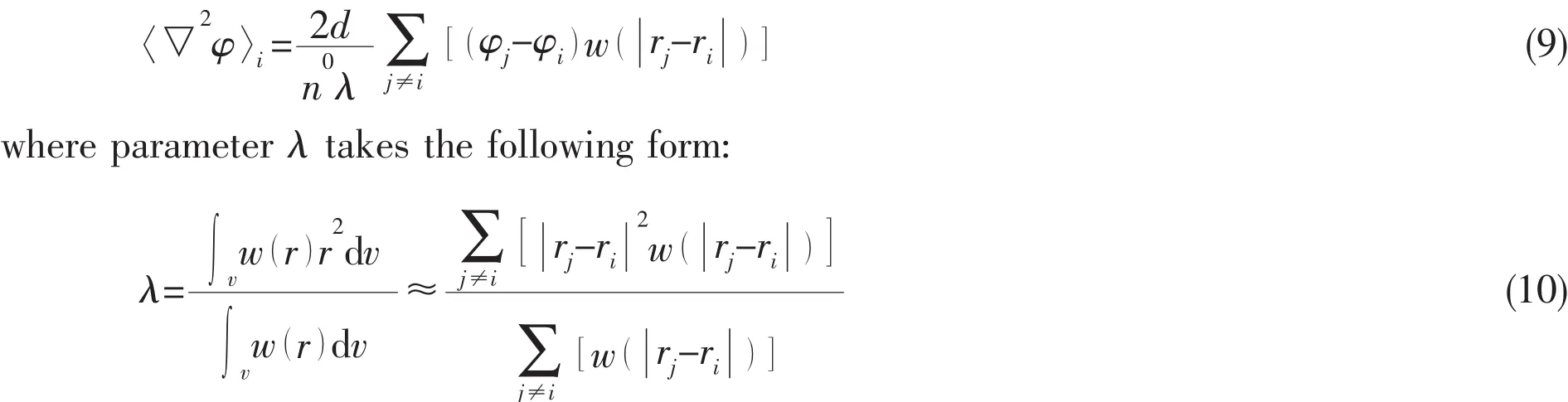
3.5 Solution algorithm for governing equations

To solve the momentum equation,a fractional step scheme is applied in each time step△t.

(1)Predicting the temporal variablesat the particle i explicitly considering the viscous terms and the body force terms.

(2)Computing the temporal particle number density n*at the temporal locationSince n*unequals n0commonly,so n*needs to be modified to n0to satisfy the incompressible conditions.This procedure is shown as follows:

(3)Obtaining the field pressure pn+1by solving the Tait’s equation of state.

For the WC-MPS method[3],the fluid pressure is directly determined by the Tait’s equation of state of the fluid:

where,γ=7 and the numerical sound speed c0in the reference fluid is determined as ten times as the maximum velocityto satisfy the weakly compressible assumption of the density variation within 1%of the reference fluid[3].Theis obtained by the Courant-Friedrichs-Lewy conditionin which △t and △l are time step and particle distance,and ccflis courant number within 0.0～1.0 and is selected as 0.25 in this study.Using this explicit formulation,the fluid pressure is directly computed with high efficiency compared with solving Poisson’s equation by traditional MPS.

(4)Updating the final particle velocityand positionby the pressure gradient terms.

3.6 Free surface

For the particles near the free surface,their particle number densities decrease compared with initial particle number density n0.Therefore,the particle can be recognized as a surface particle if the temporal particle number densitysatisfies the conditionand the pressure is treated as air pressure.Here the value of β is used as 0.97[1].

3.7 Solid boundaries

Near the solid boundaries,the fluid particle number density decreases and the corresponding particle is falsely recognized as a surface particle.To avoid this error,the ghost particles[2]are introduced and placed in layers beyond the solid boundaries.The layer number is selected as three according to effective radiusbeing the particle distance.Also these ghost particles are only involved in the calculation of the particle number density,instead of the field pressure and fluid velocities.In Fig.1,a typical layout of the ghost particles is shown.

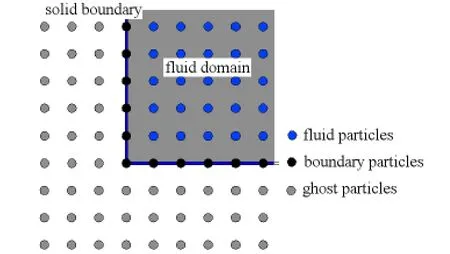
Fig.1 A schematic view of the solid boundaries

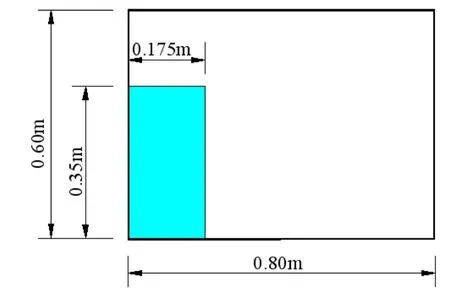
Fig.2 Geometry of the flow domain

4 Numerical results

4.1 Dam-break case1

The present dam-break case is based on Hu’s experiments[16].The geometry of the flow domain is shown in Fig.2.Here the factors of both particle distance l0and turbulence Smagorinsky constant Csare specially studied to find their influence on numerical results.Therefore,the factor of the particle distance l0is firstly investigated and selected as 0.008 m,0.006 m and 0.004 m respectively,to find the discipline of their influence on the simulation results and a better choice of the particle distance.Based on this better particle distance,three different values of the turbulence Smagorinsky constant Csare considered and compared with their simulation results,to determine a suitable constant value.And here Csconstants are determined as 0.12,0.15 and 0.18.

In this case,the initial water column is restricted in the left part of the tank by a gate.When the gate is open with a quick speed,the water will flow rightwards under the gravity and experience the evolution of free surfaces.Here the total simulation time lasts for 0.99 s,so the water column will firstly travel along the tank bottom,and then hit the right tank wall and climb along it until approaching the tank top,and finally fall down.During this process,the evolution of free surface considering l0=0.004 m and Cs=0.18 is shown at four typical instants in Fig.3.Comparing with experimental snapshots[16],we can see that they have good agreements with each other.Also,for three numerical cases under different particle distances without turbulence model,their WC-MPS simulation results are presented in Fig.4,which shows the dimensionless positions of the water front along the tank bottom against the dimensionless time.By comparison,it can be concluded that the simulation results tend to be stable with the decreasing of the particle distance.Therefore,the influence of three different Csconstants is studied for l0=0.004 m.The corresponding numerical results and the experimental data provided by Hu[16]and Martin[17]are revealed in Fig.5.Generally speaking,the numerical results for Csequaling 0.12,0.15 and 0.18 all resemble experimental data closely especially when dimensionless time is within 2.0.But having a detailed study,it can be observed that the simulation re-sults have a better agreement with the experimental data with the increasing of the constant Csespecially when dimensionless time is beyond 2.0.The reason of this conclusion physically lies in the process of the free surface evolution.As explained before,the water column experiences smooth free surface profiles at the initial stage,and then violent and largely deformed free surface profiles occur with fast water front velocity in the later stage,resulting in a typical turbulence flow.Therefore,the turbulence model with a larger Csvalue can better reveal this kind of flow characteristics.As a result,we can see that the LES turbulence model with Cs=0.18 has the best simulation result,especially when dimensionless time is larger than 2.0.

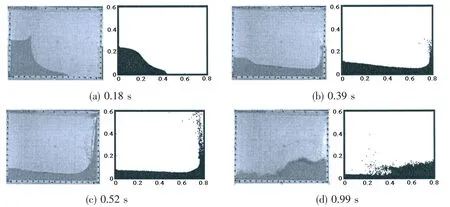
Fig.3 Comparison of free surface profiles between experimental results[16]and WC-MPS results with l0=0.004 m

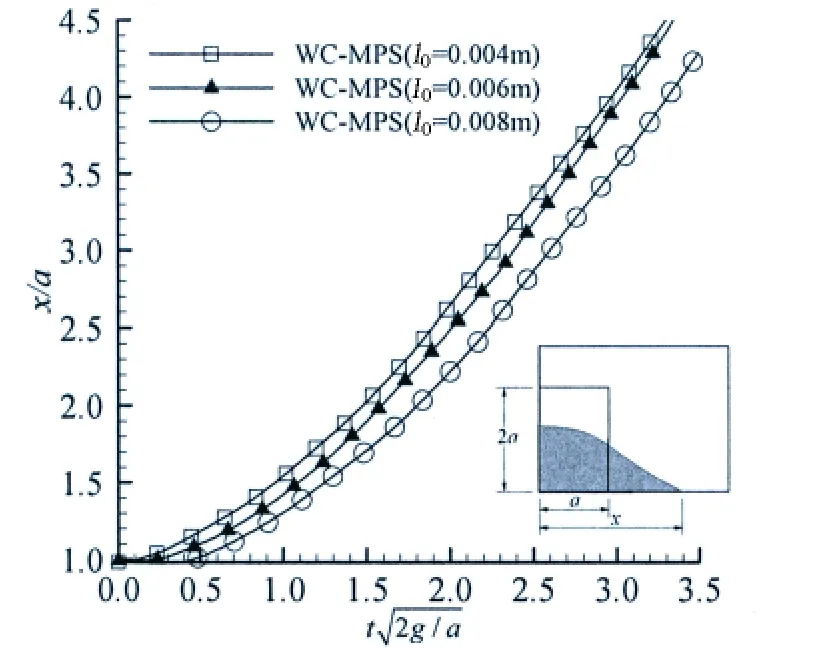
Fig.4 Numerical results of the water front positions along the tank bottom with different particle distances

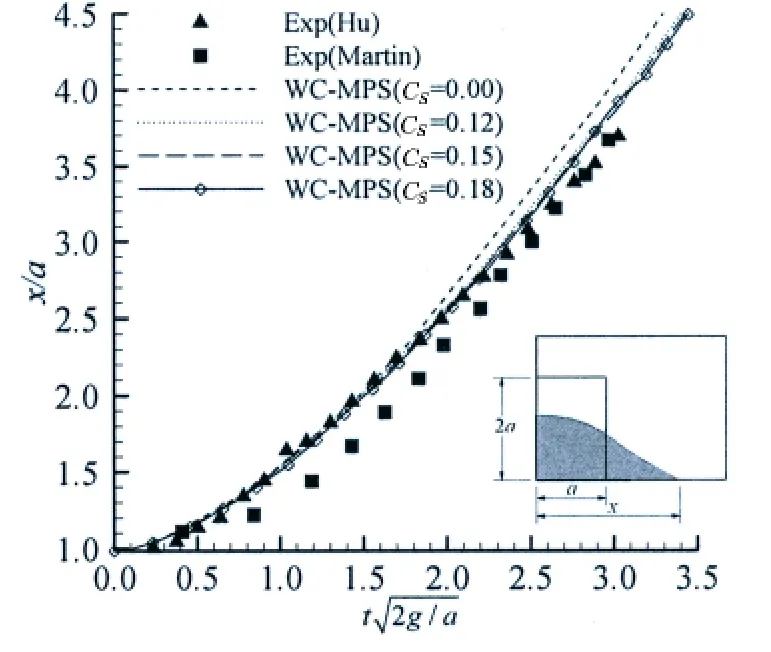
Fig.5 Experimental[16-17]and numerical results of the water front positions along the tank bottom with different Csnumbers

4.2 Dam-break case2

In this dam-break case[18],a rectangular obstacle is placed vertically in the middle of the tank bottom as shown in Fig.6.The dimensions of the whole fluid domain are 0.584 m long,and 0.438 m high.And the particle distance l0is determined as 0.002 m,so in the whole flow domain 14 782 particles are generated totally,including 10 658 fluid particles,1 022 wall par-ticles and 3 102 ghost particles.Also according to the first case,the turbulence Smagorinsky constant Csis set as 0.18.

Initially the water column remains still by the gate.With the opening of the gate quickly,the water column travels in the right direction driven by the gravity.And it hits the obstacle in the middle of the bottom wall,and jumps up quickly into the air,shaped like a tongue.Because of the inertia effect,one part of the free surface moves upper right continuously,and approaches the right wall and climbs up to the tank top.While the other part falls down and piles up on the bottom wall.During this process,some typical free surface profiles at five different instants are displayed in Fig.7.In this figure,it is clear that the WC-MPS simulation results are well consistent with experimental results[18]particularly at first four instants.

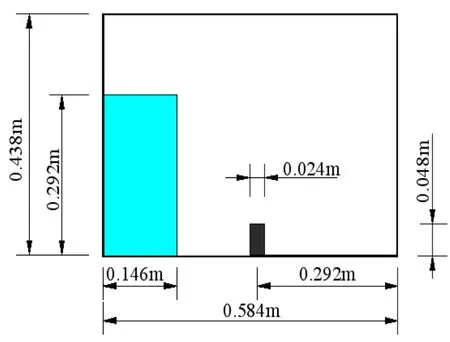
Fig.6 The sketch of the flow domain with an obstacle

Fig.7 Comparison of free surface profiles between experimental snapshots[18]and WC-MPS numerical results

5 Conclusions

In this paper,the WC-MPS method with turbulence model is applied to simulate the dam-break flow problems.For this method,the fluid pressure is directly obtained by the Tait’s equation of state of the fluid,and the turbulence terms is computed by the LES Smagorinsky model.Through the numerical studies of two dam-break cases,we can conclude as follows:

(1)The WC-MPS method has a good ability for the numerical simulation of the fluid flow with largely deformed free surface.

(2)Within the range of the computation capacity,the WC-MPS method with a smaller particle distance can better depict the fluid flow.

(3)For the violent free surface flow problems,the WC-MPS method considering the LES turbulence model with a larger Smagorinsky constant has a better numerical simulation results.

[1]Koshizuka S,Oka Y.Moving-particle semi-implicit method for fragmentation of incompressible fluid[J].Nuclear Science and Engineering,1996,123(3):421-434.

[2]Koshizuka S,Tamako H,Oka Y.A particle method for incompressible viscous flow with fluid fragmentation[J].Computational Fluid Dynamics Journal,1995,4(1):29-46.

[3]Shakibaeinia A,Jin Y C.A weakly compressible MPS method for modeling of open-boundary free-surface flow[J].International Journal for Numerical Methods in Fluids,2010,63(10):1208-1232.

[4]Xu Gang,Duan Wenyang.An investigation of MPS algorithm for free surface flow simulation[J].Journal of Harbin Engineering University,2008,29(6):539-543.

[5]Zhang Yuxin,Wan Decheng.Numerical simulation of liquid sloshing in low-filling tank by MPS[J].Chinese Journal of Hydrodynamics,2012,27(1):100-107.

[6]Koshizuka S,Nobe A,Oka Y.Numerical analysis of breaking waves using the moving particle semi-implicit method[J].International Journal for Numerical Methods in Fluids,1998,26(7):751-769.

[7]Gotoh H,Sakai T.Key issues in the particle method for computation of wave breaking[J].Coastal Engineering,2006,53(2):171-179.

[8]Shibata K,Koshizuka S,Sakai M,et al.Lagrangian simulations of ship-wave interactions in rough seas[J].Ocean Engineering,2012,42(1):13-25.

[9]Shibata K,Koshizuka S.Numerical analysis of shipping water impact on a deck using a particle method[J].Ocean Engineering,2007,34(9):585-593.

[10]Shibata K,Koshizuka S,Tanizawa K.Three-dimensional numerical analysis of shipping water onto a moving ship using a particle method[J].Journal of Marine Science and Technology,2009,14(2):214-227.

[11]Pan Xujie,Zhang Huaixin,Lu Yuntao.Numerical simulation of viscous liquid sloshing by Moving-Particle Semi-Implicit method[J].Journal of Marine Science and Application,2008,7(3):184-189.

[12]Khayyer A,Gotoh H.Enhancement of stability and accuracy of the moving particle semi-implicit method[J].Journal of Computational Physics,2011,230(8):3093-3118.

[13]Yoon H Y,Koshizuka S,Oka Y.A particle-gridless hybrid method for incompressible flows[J].International Journal for Numerical Methods in Fluids,1999,30:407-424.

[14]Gotoh H,Shibahara T,Sakai T.Sub-particle-scale turbulence model for the MPS method-Lagrangian flow model for hydraulic engineering[J].Computational Fluid Dynamics Journal,2001,9(4):339-347.

[15]Khayyer A,Gotoh H.Modified moving particle semi-implicit methods for the prediction of 2D wave impact pressure[J].Coastal Engineering,2009,56():419-440.

[16]Hu Changhong,Sueyoshi M.Numerical simulation and experiment on dam break problem[J].Journal of Marine Science and Application,2010,9(2):109-114.

[17]Martin J C,Moyce W J.An experimental study of the collapse of liquid columns on a rigid horizontal plane[J].R Soc,1952,244(882):312-324.

[18]Koshizuka S,Oka Y,Tamako H.A particle method for calculating splashing of incompressible viscous fluid[C].In:Proceedings of the International Conference,Mathematics and Computations,Reactor Physics,and Environmental Analyses,1995:1514-1521.