Numerical Solution for Ship with Forward Speed Based on Transient Green Function Method

SUN Wei,REN Hui-long,LI Hui,WANG Chuan

(College of Shipbuliding Engineering,Harbin Engineering University,Harbin 150001,China)

1 Introduction

As accurate prediction of wave-induced motions and sea loads is of crucial importance in ship design and the computer capability has rapidly advanced,using 3-D time-domain method to solve the seakeeping problem has become the essential tendency.Although this method has been studied for many decades,a robust and efficient solution is yet to develop because of the complexity of the theory and numerical solution.

For zero speed problems,the computations of transient Green function consume much more time than frequency domain Green function because of the convolution integrals.These integrals require many time steps for adequate resolution.However,for forward speed problems,the situation is reversed.The transient Green function does not change,whereas the forwardspeed Green function in frequency domain is significantly more difficult and complex with greatly increased CPU time.Therefore,at present time,active research in the area of 3-D potential flow theory for solving forward speed problem is primarily on the time domain method.

In these years,many developments have been made for numerical solution of seakeeping problems by three-dimensional time domain Green function method,such work includes Beck and Liapis(1987)[1],Korsmeyer(1988)[2]for the linearized radiation problem without forward speed,King et al(1988)[3],Magee and Beck(1988)[4],Bingham(1994)[5],Kataoka(2000)[6],Zhu et al(2009)[7]for linearized problem with constant forward speed,Lin and Yue(1990)[8],Singh and Sen(2007)[9]for body nonlinear problem with constant forward speed.These time domain solutions are formally related to the frequency domain results by Fourier transforms.

In order to develop a robust and efficient hydrodynamic solver on boundary element approach,the evaluation of transient Green function and its derivatives is one of the key points.The most commonly used numerical schemes for evaluating the memory part of the transient Green function fall in:(1)Dividing the oscillation part of the integrand into several computational domains,and part of the simulation results are obtained by linear bivariate interpolations of stored data(e.g.,Ferrant(1990)[10];Magee(1990)[11];Huang(1992)[12]);and(2)Solving the derived fourth ordinary differential equation which the transient Green function satisfied(e.g.,Clement(1998)[13];Duan and Dai(2001)[14];Shen et al(2007)[15];Tong et al(2013)[16]).

In this paper,we developed a three-dimensional time domain program based on the transient Green function method to solve the linear radiation problem with constant forward speed.The practical utility of this program was demonstrated by the accuracy of the hydrodynamic coefficients for heave and pitch.This is the focus of much of the present work.

2 Mathematical formulation

2.1 Boundary value problem

The problem is formulated in the fluid domain,which is enclosed by free surface Sf,body surface Sband infinite surface S∞,as shown in Fig.1.The earth-fixed system O-x0y0z0is chosen with the x-y plane coincident with the quiescent free surface,and z is upward;and the reference system O-xyz is moving with the ship at a constant speed U0along the positive x-axis;the two systems are coincident at t=0.

Fig.1 Fluid domain and coordinate systems

It is assumed that the fluid is incompressible,inviscid and its motion irrotational.Surface tension is not included and the water depth is infinite.In small amplitude hydrodynamic problems,the velocity potential Φ in the fluid domain can be divided into:

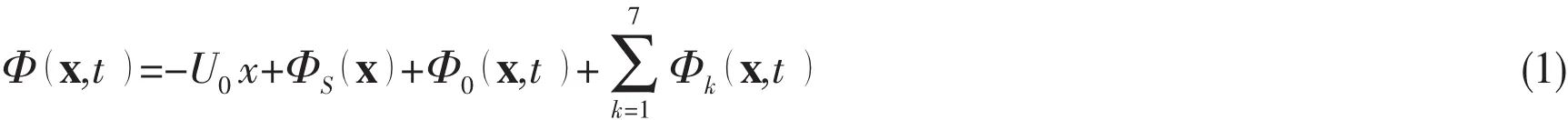
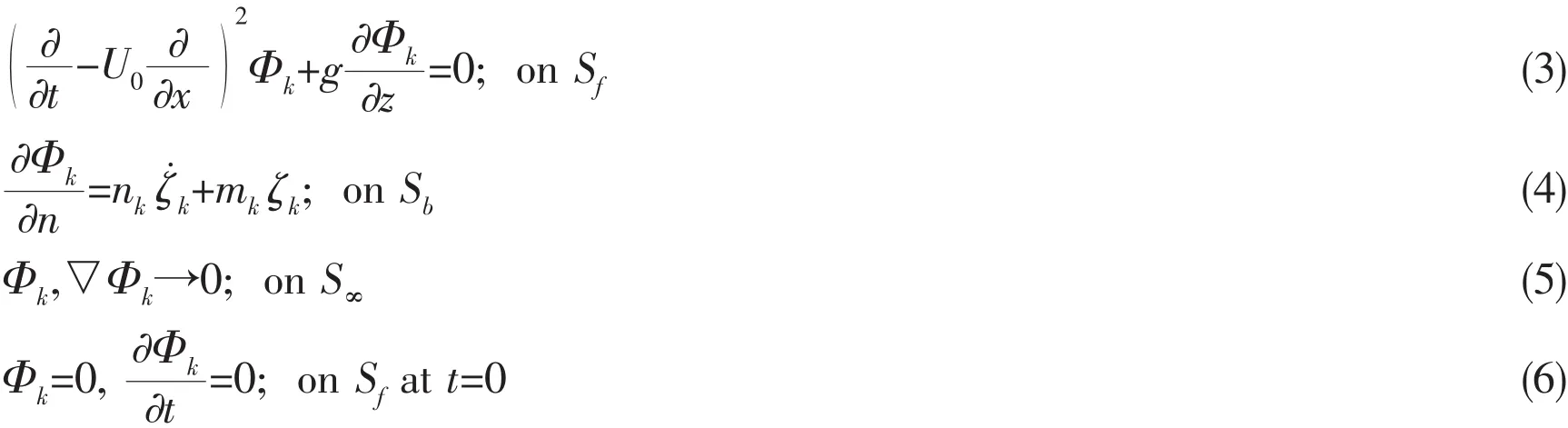
where the unite normal vector of the bodyis positive out of the fluid andis the amplitude of unsteady motion in six degrees of freedom.The steady velocities mkare defined as follows:

2.2 Boundary integral equations

By introducing the impulse response function,the radiation potential can be decomposed into impulsive part and memory part(Liapis,1986)[17]:

2.3 Hydrodynamic force

The potential for an arbitrary forced motion in k-th mode is found as the convolution ofwith the velocity of the motion after solving the above equations.The expression for the radiation force acting on the body in j-th direction due to k-th mode motion is:

根据当地常年桑树病虫害发生情况，引进抗性较强的桑树品种，并加强对引进桑苗的检疫，杜绝从外地带入桑树病虫害。如条件允许，最好使用当地的自繁苗。

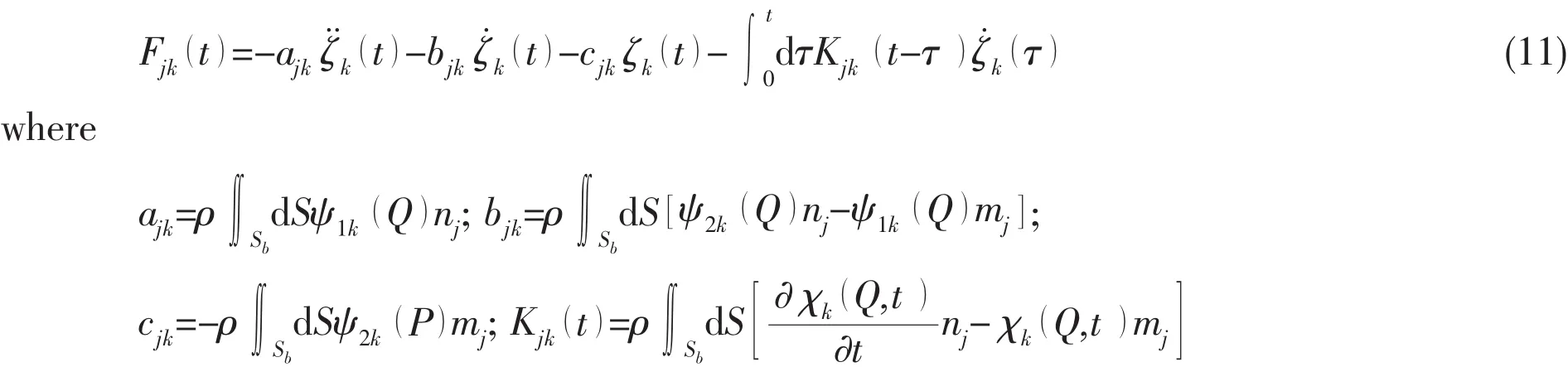
The above coefficients are related to the added mass and damping coefficients in the frequency domain by a Fourier transform(Wehausen,1971)[18]:

3 Numerical implementation

3.1 Solution of the integral equation

The Boundary Element Method is adopted to solve the formulated integral equations numerically.The solution for the velocity potential is approximated by a constant value on each element.According to the integral equations for impulse and memory potential(Eqs.(8)～(10)),they can be written to the discretized forms:

In the above expressions,i,j are the panel indices for source points and field points respectively,N is the number of panels on body surface,M△t and m△t denote the latest time and historical time,△t is the constant time step.The influence coefficients can be given by:

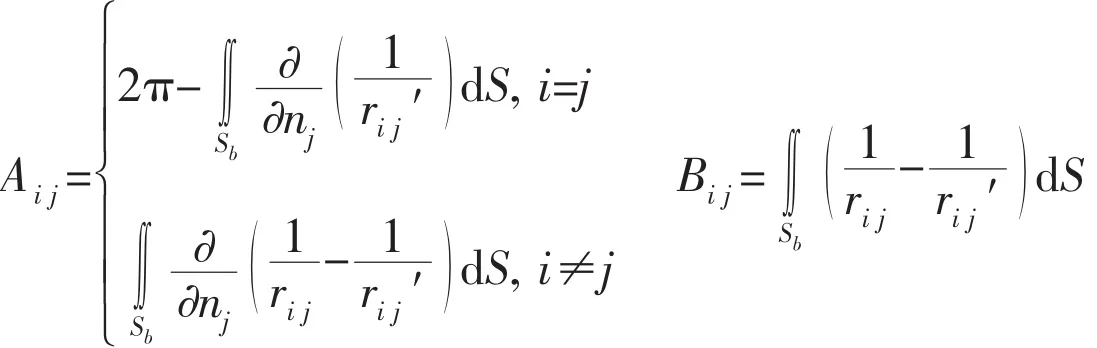
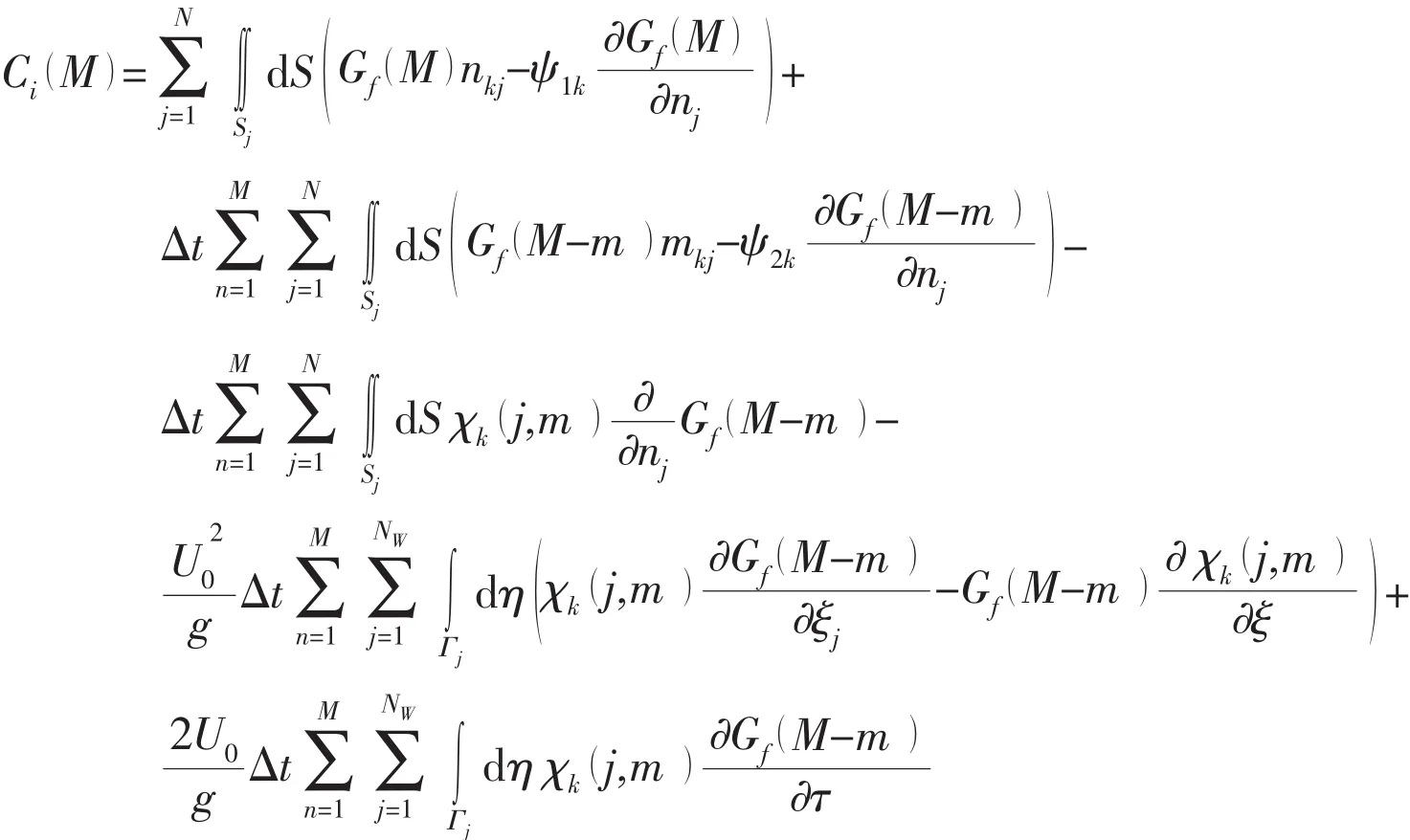
The line integral in Eq.(10)is evaluated by subdividinginto a series of straight line segments,and NWis the number of lines on waterline.By solving the above system of linear equations(Eqs.(13)～(15))at each time step,the velocity potential of each point on body surface can be obtained.

3.2 Evaluation of the transient Green function

From the influence coefficients of linear equation(Eq.(15)),we notice that the evaluation of free surface memory part of the transient Green function is one of the key points to solve the memory potentialA more convenient form offor numerical calculation is

According to Clement(1998)[13],F( μ, )β satisfies the following fourth order ordinary differential equation:

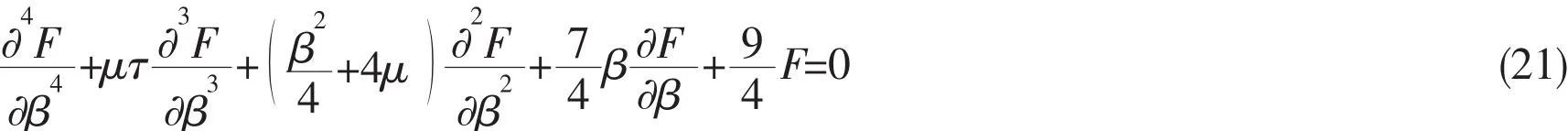
For the precise integration method,only a brief description of the general formulation is given,Eq.(17)can be organized into the following form:

The details solution process are given by Tong(2013)[16],and hence not repeated here.

4 Numerical results

Numerical computations were performed for linearized radiation problem on a Wigley hull with forward speed,and the results were compared with experimental values and reference results computed by Kataoka(2000)[6].The main dimensions and experimental data for Wigley hull forms were presented by Journée(1992)[19].The Wigley III hull form has a beam to length ratiobeam to draft ratioand volume of displacement▽=0.078 m3.The half beam is given by:

The view of panels distributed on body surface is shown in Fig.2.The panel number is N=312,which is less than N′=400 in Kataoka’s work.The line number is NW=78 in present work.The constant time step is△t=0.01,which is small enough for obtaining accurate results.

Fig.2 Panels distributed on the Wigley III hull

The non-dimensional added mass and damping coefficients of Wigley hull moving at Froude number Fn=0.2 are shown in Fig.3 and Fig.4 versus non-dimensional frequency

For the diagonal coefficients(Fig.3),the added mass terms A33and A55compare well to experimental data and reference results,while the damping coefficients B33and B55perform well for larger frequencies but show a deviation at lower frequencies.For the off-diagonal coefficients(Fig.4),the deviations of added mass terms A35and A53from experiment are primar-ily at lower frequencies.For damping coefficients B35and B53,the results in this paper and reference results are both reasonably close to experimental measurements.

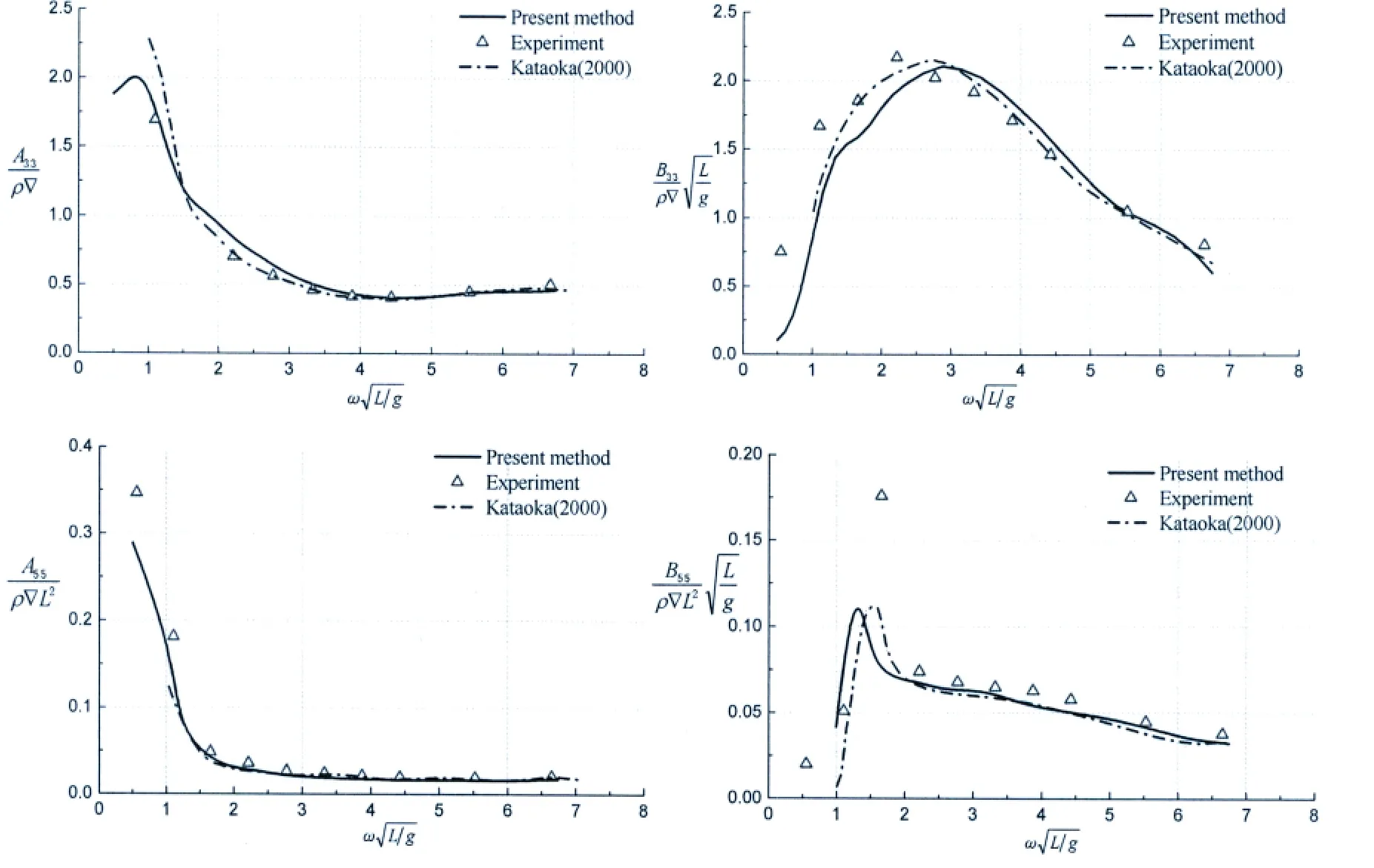
Fig.3 Added mass and damping coefficients for heave and pitch of Wigley III hull(Fn=0.2)

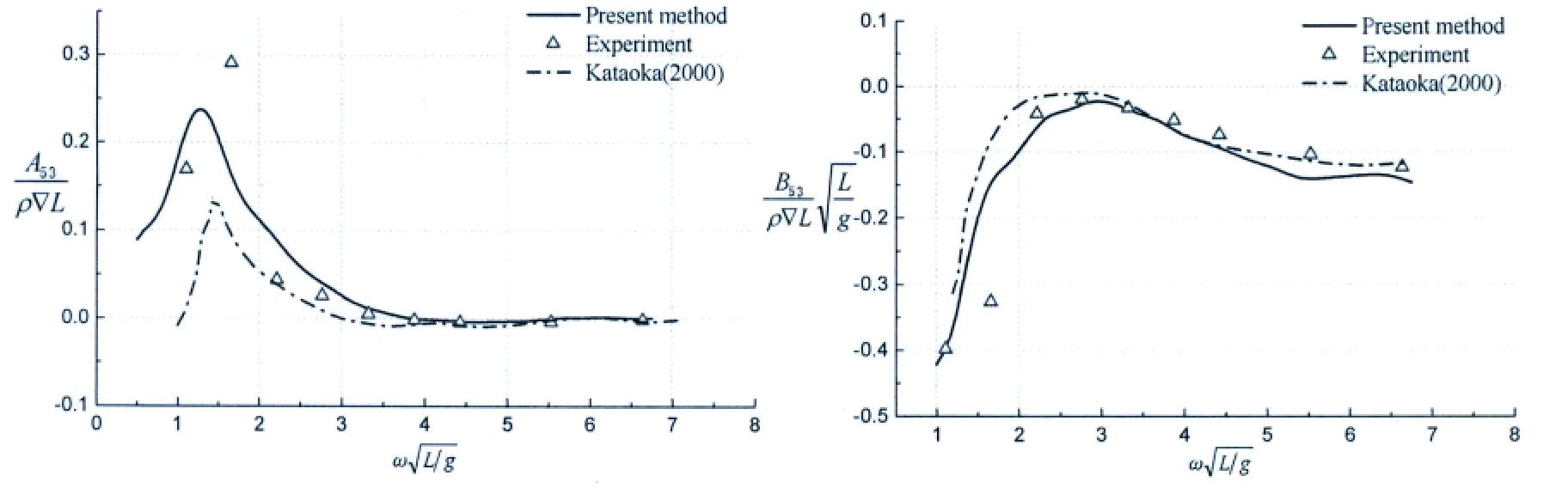
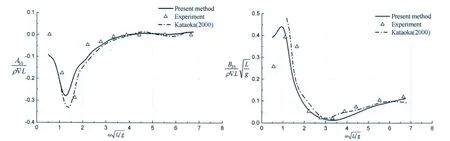
Fig.4 Coupled added mass and damping coefficients between heave and pitch of Wigley III hull(Fn=0.2)

In summary,we see that the results obtained by the 3-D time domain program based on transient Green function method for hydrodynamic coefficients are reasonably satisfactory comparing with experimental data,and are generally better than reference results at lower frequencies.

5 Conclusions

The three-dimensional time-domain Green function method for studying the behavior of ship in waves at constant forward speed has been developed,by formulating the basic hydrodynamic problem and numerically solving it through the implementation of the theoretical method.The precise integration method was employed to solve the ordinary differential equations that the transient Green function satisfied.The horizontal and vertical derivatives can be obtained directly through the deriving relationships,which can reduce the CPU time evidently.The investigation of added mass and damping coefficients for heave and pitch were performed for a Wigley hull.From the comparisons between experimental data and reference results,we can conclude that the numerical scheme is quite robust and has a good accuracy,even though some more hull forms are needed to validate here.

[1]Beck R F,Liapis S J.Transient motions of floating bodies at zero forward speed[J].Journal of Ship Research,1987,31(3):164-176.

[2]Korsmeyer F T.The first and second order transient free-surface wave radiation problems[D].Ph.D.Thesis,Dept.Ocean Eng.,MIT,Cambridge,Massachusetts,1988.

[3]King B W,Beck R F,Magee A R.Sea-keeping calculations with forward speed using time domain analysis[C]//Proc.17th Symp.Naval Hydrodynamic.The Hague,Netherlands,1988.

[4]Magee A R,Beck R F.Compendium of ship motion calculations using linear time-domain analysis[R].Dept.Naval Architects Marine Engineering,University of Michigan,Ann Arbor,Michigan,Report No.310,1988.

[5]Bingham H B.Simulating Ship Motions in the Time Domain[D].Ph.D.Thesis.Department of Ocean Engineering,MIT,Cambridge,Massachusetts,1994.

[6]Kataoka S,Sueyoshi A,Arihama K,Iwashita H,Takaki M.Seakeeping computation of ships with forward speed in waves by a time-domain Green function method[R].Transactions of the West-Japan Society of Naval Architects,Report No.101:49-61,2000.

[7]Zhu H R,Zhu R C,Miao G P.The numerical simulation on the interaction between waves and ships with forward speed based on the method of time domain Green’s function[J].Journal of Hydrodynamics,2009,Ser.A,24(5):613-621.

[8]Lin W M,Yue D K P.Numerical solutions for large amplitude ship motions in the time domain[C]//In:Proceedings of the 18th Symposium on Naval Hydrodynamics.The University of Michigan,Ann Arbor,Michigan,1990.

[9]Singh S P,Sen Debabrata.A comparative linear and nonlinear ship motion study using 3-D time domain methods[J].Journal of Ocean Engineering,2007,34:1863-1881.

[10]Ferrant P.A coupled time and frequency approach for nonlinear wave radiation[C]//Proc.18th Symposium on Naval Hydrodynamics.The University of Michigan,Ann Arbor,Michigan,1990.

[11]Magee A R.Large amplitude ship in the time domain[D].Ph.D.Thesis.Department of Naval Architecture and Marine Engineering,The University of Michigan,Ann Arbor,Michigan,1990.

[12]Huang D B.Approximation of time-domain free surface function and its spatial derivatives[J].Journal of Shipbuilding of China,1992(1):16-25.

[13]Clement A H.An ordinary differential equation for green function of time-domain free-surface hydrodynamics[J].Journal of Engineering Mathematics,1998.

[14]Duan W Y,Dai Y S.New derivation of ordinary differential equations for transient free-surface Green functions[J].China Ocean Engineering,2001,15(4):499-507.

[15]Shen L,Zhu R C,Miao G P,Liu Y Z.A practical numerical method for deep water time-domain Green function[J].Journal of Hydrodynamics,2007,Ser.A,22(3):380-386.

[16]Tong X W,Ren H L,Li H,Shan P H.Evaluation of 3D time domain green function based on the precise integration method[J].Journal of Ship Mechanics,2013,17(9):991-997.

[17]Liapis S J.Time-domain analysis of ship motions[D].Ph.D.Thesis.Department of Naval Architecture and Marine Engineering,The University of Michigan,Ann Arbor,Michigan,1986.

[18]Wehausen J V.The motion of floating bodies[J].Annual Review of Fluid Mechanics,1971,3:237-268.

[19]Journée J M J.Experiments and calculations on four Wigley hull forms[R].Faculty of Mechanical Engineering and Marine Technology,Delft University of Technology,Report 0909,1992.