Application of the Improved Collaborative Optimization on Ships’Conceptual Design

YAO Zhuang-le,CHEN Chao-he

(Naval Architecture and Ocean Engineering R&D Center of Guangdong Province,South China University of Technology,Guangzhou 510641,China)

1 Introduction

Modern ship design is a multidisciplinary,multi-field project,which involves floating,resistance,structure,stability,seakeeping and other disciplines,and there are many interaction,mutual influences among the various disciplines.However,traditional ship design process is a serial design pattern,namely,different designers targeted optimize different design disciplines of ship in a certain order.The optimization resulting in previous discipline will be one of the constraints of subsequent discipline.This optimization process cannot fully consider the relation among different disciplines,and reduces the feasibility of optimization results.It usually could not get the real system optimal solution.At the same time,as ship design issues are complicated,the serial design pattern is increasingly difficult to meet the design requirements.Hence,it is necessary to introduce a method that considers the overall coupling relationships among the various disciplines.

In aircraft design,the designers also face complex issues of multidisciplinary interaction.So in the 1980s,a group of aerospace scientists and engineers,represented by Sobieszezaoski Sobieski and IlanKroo,have proposed the optimization methods for the complex systems de-sign[1].With the perfection of these idea,they gradually form the present multidisciplinary design optimization method(MDO).Through research,the method can also solve the above problems in ship design,and it must have wide development space and realistic significance in the field of ship design.

Currently,the main MDO algorithms are:multidisciplinary feasible method(MDF),individual disciplinary feasible method(IDF),concurrent subspace optimization(CSSO),collaborative optimization(CO)and Bi-Level integrated system synthesis(BLISS),etc.These several algorithms above have different source,purpose,optimization of process,advantages and disadvantages and application.According to the specific condition of ship design problem,most academics agree that the CO algorithm based on approximate model and BLISS 2000 algorithm are more suitable multidisciplinary optimization algorithm in ship design[2].Here,this paper focuses on collaborative optimization and its improvement methods,and introduces the examples of its application in ship design.

2 Collaborative optimization and its improvement

2.1 Algorithm introduction

In the 1990s,a new type of MDO algorithms—the CO algorithm was proposed by professor Kroo et al[3]at Stanford University,and it used consistency constraints to process the system decomposition and coordination problems.Its basic design idea is:system level distributes system level target variable to all sub-discipline level.The sub-discipline level attempts to satisfy the constraint conditions in respective discipline,and its target makes the difference between discipline coupled variable and system level target value minimum.After sub-discipline level is optimized,the coupled variable passes back to system level,and constitutes consistency constraint information of system level,which settles the inconsistency of coupled variable between sub-disciplines.When system level finishes the optimization,it will distribute new target to all sub-discipline.After many iterations,the algorithm will end up with a optimal scheme which has the best consistency between each sub-discipline[4].The structure of algorithm is shown in Fig.1.

CO algorithm can analyze each sub-discipline in parallel,and eliminate complex system analysis process,but the original CO algorithm is imperfect.In system level of original CO algorithm,the constraint condition isonly when all sub-discipline optimization results returning to the system are equal,it can satisfy the constraints.So the condition of system level meeting all equality constraint at the same time is:all sub-discipline optimization objective functions values are zero.This is an ideal state,and in general,the feasible region of system level optimization problem may not exist.At the same time,due to the discrete of Jacobian matrix of consistency constraint at the optimum solution,or the absent of the Lagrange multiplier of Kuhn-Tucker conditions,result in system level optimized problem cannot satisfy Kuhn-Tucker conditions[5].Because of the above disadvantages,it will face a serious calculation problem in CO algorithm,so it requires improvement.

Fig.1 The structure of the collaborative optimization

2.2 Algorithm improvements

At present,there are academics study the improvement of CO algorithm,and they put forward some improving measures.Braun et al[6]put forward improving measures of penalty function of sub-discipline and the relaxation factor method.Sobieski,Kroo et al[7]used response surface techniques to improve CO algorithm.Han et al[8]presented measures of improved subsystem consistency constraint and system-level penalty function.Li et al[9]proposed adaptive penalty function for CO algorithm as improving measures.Based on the analysis above and combining previous improving program,this paper uses the dynamic penalty function method to rebuild system level optimization problem,and transforms it into an unconstrained optimization problems.According to the requirements of different sub-discipline constraint weight,it distributes different penalty factors to different sub-disciplines.

In order to eliminate the consistency equality constraint among sub-disciplines,all equality constraints in system level shall be a penalty term,and add to the objective function of the system level.Hence,the objective function in system level needs to be transformed into the following formula.

In the process of system level optimization,the existence of the penalty term will force the optimization results of objective function to approach consistency information among disciplines.It makes the next system level target meet interdisciplinary constraint better,and finally gets an optimal solution.The optimization solution not only satisfies the requirement of consistency information among disciplines,but also achieves the optimum objective function.

The key to deal with constraint problem in the form of penalty function is the selection of penalty factor γi.But the fixed value γiis not conducive to optimal,so dynamic penalty factors need to be taken.In addition,the influence of different disciplines consistent constraint on the system is different,so it can assign different penalty factor to different disciplines constraint information in specific situation.It can increase the weight of individual discipline constraint information.

Using inconsistent information among disciplines to build up the dynamic penalty factor,we get the following formula:

where:b,m and a are constants,k is the inconsistent information among disciplines.

When selecting the initial value of b,we at first keep it with the final system objective function values in the same magnitude,and then adjust its value according to the result of optimization.The m and a,are associated with the accuracy requirement of consistent information among disciplines,and a usually is positive integer,a=1;when value of a is fixed,the bigger the value of m,the higher the requirement of consistent information among disciplines will be.Inconsistent information among disciplines are defined as follows:

where:J1,J2,…,Jnrepresent the optimization objective function value of each sub-discipline;X1,X2,…,Xnrepresent the optimization results of each discipline;z1,z2,…,znrepresent the target expectation that system level assign to each discipline.

3 Examples of application

This paper shows a conceptual design example of 300 t small waterplane area twin-hulls(SWATH)ship[10](see Fig.2).According to the simplified optimization model,we apply the above methods to optimize the two disciplines of resistance and structure.The main parameters of SWATH show in Tab.1.

The design of this example uses multidisciplinary design optimization method to optimize the SWATH under the condition of invariable displacement,and achieves the minimum fuel consumption.Fuel consumption is related to the speed,the hull weight,the resistance,the engine efficiency,and so on.The speed is a uncertain value according to different purposes,and the engine efficiency in-volves the selection of the engine.Therefore,we mainly select the hull weight and resistance primary as the factors in the design process.The entire system can be divided into the structure sub-discipline and the resistance sub-discipline.The design variables and its variable ranges are shown in Tab.2.

Fig.2 A 300 t small water-plane area twin hulls

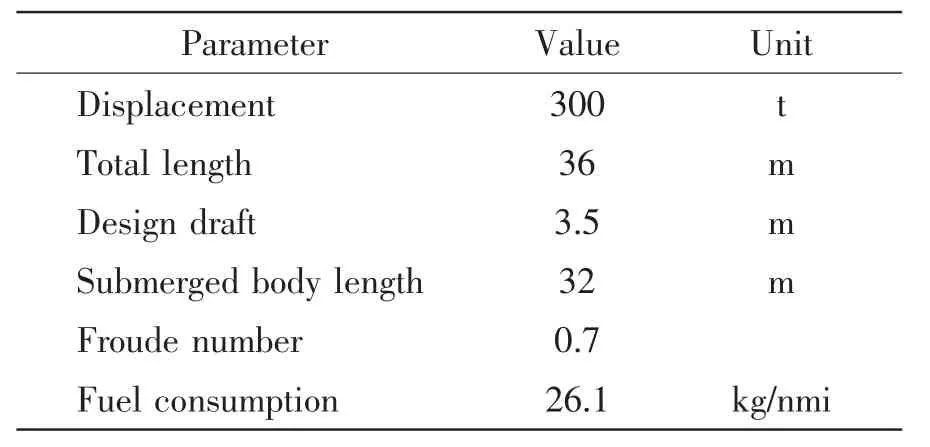
Tab.1 The main parameters of SWATH

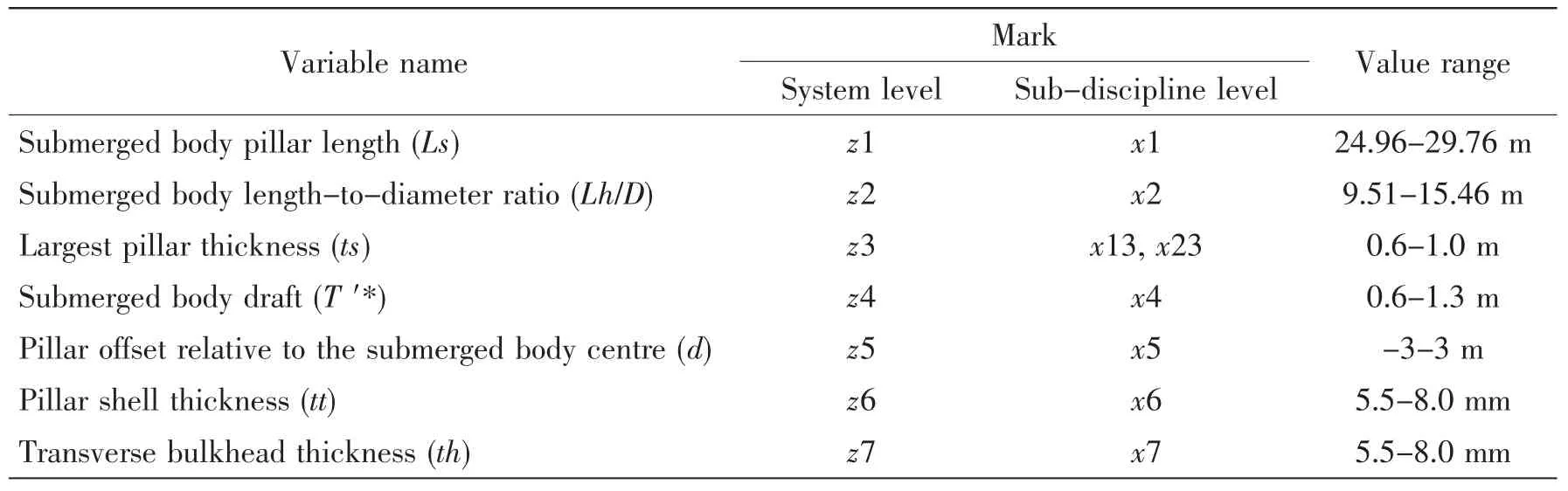
Tab.2 The system design variables and variable ranges

In order to save computational cost and improve the computational efficiency,Kriging surrogate model in the calculation of two sub-disciplines of structure and resistance are applied,which can solve their corresponding response values.

According to surrogate model-based CO framework,the multidisciplinary design optimization problem of SWATH will decompose into a system level,a resistance optimization sub-discipline and a structure optimization sub-discipline.Based on the overall target and consistency constraints,the mathematical model of the overall framework have been established.

Export:W0,S

where:C represents fuel consumption;Cvrepresents viscous resistance coefficient;Cwrepresents wave-making resistance coefficient;W0represents total weight of the ship;S represents the maximum structural stress,and limits to 255 MPa.

Particle swarm optimization algorithm as solving algorithm is used to solve the optimization problem.The results as shown in Tab.3,and the initial and optimal values of design variables as shown in Tab.4.

Tab.3 Results comparing

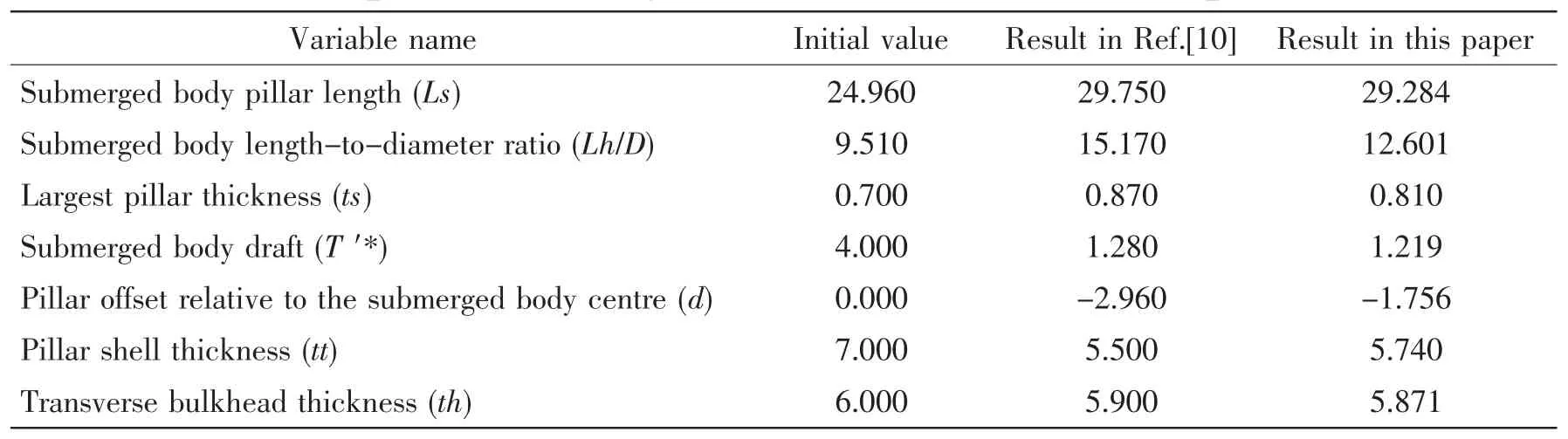
Tab.4 Comparison of design variable before and after optimization

From the two forms above,compared to the initial solution,each parameter of the optimal solution in this paper is improved:the wave-making resistance coefficient Cwhas a clear decrease;the maximum structure stress S is less than 255 MPa,which meets the design requirements.Eventually,the fuel consumption C is decreased by 10.767%.Compared to the optimal solution in the Ref.[10],it also has a better improvement(about 2.143%),and the value of each variable satisfies various constraints.It proves that the application of improved collaborative optimization in ships’conceptual design is feasible and effective.

4 Conclusions

This paper expounds the broad application prospect of multidisciplinary design optimization in ship design,and specially describes the collaborative optimization,and its problems are improved.Inter-disciplinary inconsistency information is used to construct dynamic penalty factor in system level objective function,and a new form of objective function is proposed.Meanwhile,according to different constraint conditions in sub-discipline,different penalty weights are chosen as its dynamic penalty factor.Dynamic penalty function eliminates the existing consistency equality constraints,and greatly improves the calculation accuracy.At last,this algorithm is used to solve the resistance and structure optimization problems of a SWATH,and the final results show that it has a clear decrease in the fuel consumption.It proves that the algorithm has a better application effect in ship conceptual design.

[1]AIAA Multidisciplinary Design Optimization Technical Committee.Current state of the art on multidisciplinary design optimization(MDO)[C].An AIAA White Paper,September,1991.

[2]Jiang Zhe,Cui Weicheng.A comparison of multidisciplinary design optimization algorithms and their application to the design of ships and offshore platforms[J].Journal of Ship Mechanics,2009,13(1):150-159.

[3]Kroo I M,Altus S,Braun R D,Gage P,et al.Multidisciplinary optimization methods for aircraft preliminary design[C]//AIAA-94-4325-CP,the 5th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization.Panama City Beach,Florida,Sept.7-9,1994:697-707.

[4]Wang Xiaoqing,Wang Xiaojun.Algorithm of multidiscipline optimization design[J].Missile and Space Vehicle,2007,1:23-26.

[5]Li Haiyan,Jing Yuanwei,et al.Collaborative optimization algorithm based on dynamic penalty function method[J].Control and Decision,2009,24(6):911-915.

[6]Braun R D,Gage P,Kroo I.Implementation and performance issues in collaborative optimization[R].AIAA-96-4017,1996.

[7]Sobiesxil P,Kroo I.Collaborative optimization using response surface estimation[R].AIAA-98-0915,1998.

[8]Han Minghong,Deng Jiati.Improvement of collaborative optimization[J].Chinese Journal of Mechanical Engineering,2006,42(11):34-38.

[9]Li Haiyan,Ma Mingxu,et al.New adaptive penalty scheme for collaborative optimization[J].Journal of System Simulation,2009,21(19):6178-6182.

[10]Xu Jie.The research and application on a multidisciplinary design optimization approach to SWATH[D].Huazhong University of Science and Technology,2009.