基于数学建模过程系统化的高职数学课程开发

贺楚雄

(江西工业工程职业技术学院基础部，江西萍乡 337000)

基于数学建模过程系统化的高职数学课程开发

贺楚雄

(江西工业工程职业技术学院基础部，江西萍乡 337000)

本文以高职矿山机电专业应用数学课程为例，采用基于工作过程系统化的课程开发理论和方法，对高职数学课程开发进行探讨。从体现课程定位的开发理念、基于数学建模过程系统化的开发思路、基于数学建模过程的教学基本程序、基于行动导向的教学方法和基于整体思考的评价方式等方面对基于数学建模过程系统化的高职数学课程开发进行论述。

高职数学；数学建模过程；工作过程系统化；课程开发

高职数学课程是高等职业教育各专业的一门必修课程，其传统的课程定位来源于学科体系的数学课程，强调基础性和工具性，强调学科知识的系统性，已不能体现高职教育的特点和规律。高职数学课程的定位应向“人文素质课、数学工具课、发展基础课和职业核心能力课”四位一体的课程定位转变[1]，高职数学课程要追求基于工作过程的系统化而不是学科结构的系统化。

一、对数学建模过程的认识

数学建模过程可分为模型准备、模型假设、模型建立、模型求解、模型分析、模型检验和模型应用等7个步骤。它以应用数学知识解决实际问题为工作任务，以建立解决实际问题的数学模型为工作成果。在整个数学建模的过程中，需要综合运用专业能力、方法能力和社会能力，它的对象、内容、手段、组织、产品和环境时刻处于运动状态，始终遵循着资讯、决策、计划、实施、检查和评价等几个相对固定的环节。

基于工作过程的课程观和基于学习情境的建设观是职业教育的两个重要类型特征，因此，职业教育应按工作过程的顺序开发课程，职业教育的教学应以情境教学为主[2]。高职数学课程应在应用数学知识解决实际问题的情境中开展教学，应以应用数学知识解决实际问题为基本工作任务。它们的工作过程实际上就是数学建模过程，因此，可以采用基于工作过程系统化的课程开发方法[3]，开发基于数学建模过程系统化的高职数学课程。

二、基于数学建模过程系统化的高职数学课程开发

矿山机电专业是江西工业工程职业技术学院（以下简称“我院”）省级示范高职院校建设项目中的重点建设专业之一，也是江西省特色专业。我院按照工作过程系统化的思想，将矿山机电专业技术领域岗位（群）的典型工作任务，归纳成职业行动领域，并转换成学习领域，形成课程体系。矿山机电专业学习领域课程分为职业核心能力学习领域课程、专业基本技能学习领域课程、专业核心技能学习领域课程、职业能力拓展学习领域课程和其他素质拓展学习领域课程五类，而应用数学是该专业一门必修的职业核心能力学习领域课程。在矿山机电专业应用数学课程开发建设的过程中，要始终坚持“立足素质，服务专业，强调应用，发展能力”的基本理念。

1.通过“立足素质”，实现数学课程的文化价值，体现人文素质课的目标定位

现代动态的教育观认为，目标外显的以就业为导向的职业教育绝不是一种等同于一般职业培训的纯功利性的教育活动，而是教育的一种类型，同样要做到既满足社会发展需求，又满足个性发展的需要。职业教育依然要高举以人为本、促进人的全面发展的大旗[2]。数学是人类文明发展史上理性智慧的精华，数学文化即数学的思想、精神、方法、观点、语言以及它们的形成和发展，是人类文化的重要组成部分，是人类进步所必需的文化素质和修养，在形成人类理性思维和促进个人智力发展的过程中发挥着独特的、不可替代的作用[4]。矿山机电专业应用数学课程应实现数学的人文素质教育功能。

2.通过“服务专业”，精选教学内容，体现发展基础课的目标定位

数学科学既是自然科学、技术科学等科学的基础，又是学生进一步进行专业学习、深造和终身发展的基础。矿山机电专业应用数学课程必须为专业后续课程服务，为学生学习后继课程提供必要的数学基础知识和基本技能，使学生能可持续发展。

3.通过“强调应用”，培养学生应用数学的意识，体现数学工具课的目标定位

数学是刻画自然规律和社会规律的科学语言和有效工具，数学的语言、符号、图像、计算、估计、推理已经渗透到日常生活与公众之中，是分析问题、解决问题的有力工具。矿山机电专业的应用数学课程必须为学生解决生产实际问题提供分析和计算的工具，让学生熟练掌握应用数学解决实际问题的过程，培养学生应用数学知识解决实际问题的能力[1]。

4.通过“发展能力”，注重学生职业能力的全面协调发展，体现职业核心能力课的目标定位

以人为本、全面发展的职业教育强调获得专业能力，更要强调获得方法能力，尤其要强调获得社会能力[2]。矿山机电专业应用数学课程在培养学生的职业核心能力上有自己的优势，应在此方面发挥应有的作用。

坚持“立足素质，服务专业，强调应用，发展能力”的基本理念，以基于工作过程系统化的课程开发理论和方法为指导，以矿山机电专业学生所需数学知识为出发点，结合学生人文素质培养的需要，合理选择教学内容。以相关数学知识的应用为基本工作任务，针对每个工作任务设计一个数学应用的实际问题，再以基本工作任务和实际问题为载体，并遵循人类认知规律，设计学习情境和教学项目。

按数学建模过程的行动体系将每个学习情境的内容进行序化，将数学的陈述性知识与数学应用的实际经验、策略等过程性知识相整合，将理论知识与实践知识相整合。

通过调研，矿山机电专业的应用数学课程应包括数学建模知识、极限、导数、微分、最优化方法、不定积分和定积分等7类数学知识。该课程应以这些数学知识的应用为基本工作任务，针对它们设计一些数学应用的实际问题，再以这些实际问题为载体，设计成7个学习情境，分别是“节约装修材料问题”、“质量非均匀物体的密度计算”、“比萨斜塔实验中铅球瞬时速度的计算”、“钢球镀铬层体积的近似计算”、“易拉罐的设计”、“运动路程的计算”和“不规则面积的计算”。每一个学习情境都是一个完整的数学建模过程，每一个学习情境都是同一范畴的数学应用实际问题，并按知识内在的逻辑联系，从简单到复杂排序，这些学习情境呈平行、递进或包容的关系[1]。如图1所示。

图1 课程内容与结构

通过7个结构化、系统化的数学建模过程的设计，能逐步使学生获得资讯、决策、计划、实施、检查、评价这样完整的思维过程训练，使得学生通过同一个范畴的具体的学习情境的比较和鉴别，形成应用数学的能力，使其在面对超出这七个学习情境之外的新的实际工作情境时，能够从容应对，使得其能力逐步从经验层面上升到策略层面[1]。

每个学习情境都是一个数学建模项目，按照数学建模过程组织教学。教学过程分为如下环节或步骤（如图2所示）。

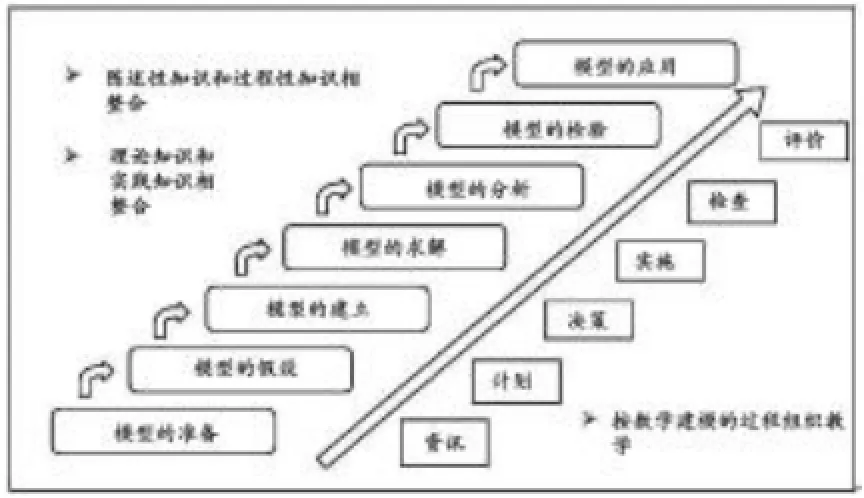
图2 教学基本程序

布置任务：该环节主要是对学生进行分组，布置工作任务。资讯：该环节主要是进行模型的准备。首先是分析所给问题的背景，提出资讯问题，再通过各种手段方式查阅、学习了解相关知识。计划与决策：该环节主要是进行模型的假设与变量说明。首先是小组成员对问题的解决进行初步分析，根据实际问题的特性和建模的目的，提出模型的假设，对涉及的变量进行说明，再在组长的主持下，完成小组的模型的假设和变量说明。实施：该环节主要是进行模型的建立和求解。首先是小组成员对问题的解决进一步进行分析，形成个人建立模型的思路，选择适当的数学工具建立相应的数学模型，并利用相关的数学工具对数学模型进行求解，再在组长的主持下，建立小组的数学模型并求解。检查：该环节主要是进行模型的分析与检验。首先是小组成员对建立的数学模型进行分析与检验，再在组长的主持下，对小组的数学模型进行分析与检验。评价与反馈：该环节主要是对整个学习情境进行评价、反思。先是个人自评，再是小组互评，然后教师评价，最后师生共同对整个学习情境进行教学反馈、总结。

这种教学具有如下特点：学生是学习过程的中心，教师是学习过程的组织者与协调者，学生在自己动手的实践中掌握技能，习得知识，从而构建属于自己的经验和知识体系。

在职业教育教学的具体实施中，根据开发的“学习领域”和构建的“学习情境”，只有采用行动导向的教学才能达到最佳的效果，并且对提高教学效果，形成新型师生关系发挥重要作用[5]。

基于数学建模过程系统化的高职数学课程的教学方法，应以项目教学法、案例教学法、头脑风暴法、引导文教学法等行动导向的教学方法为主。师生在共同实施一个完整的“项目”中完成教学活动，同时，在教学的各个环节辅以其它教学方法，例如，在布置任务环节中，通常采用引导文教学法和讲授法；在资讯环节中，通常采用引导文教学法、问题探究法、头脑风暴法、讨论法和讲授法；在计划与决策环节中，通常采用引导文教学法、头脑风暴法、讨论法和讲授法；在实施环节中，通常采用引导文教学法、头脑风暴法、讲授法和练习法；在检查环节中，通常采用引导文教学法、头脑风暴法、讨论法和讲授法；在评价与反馈环节中，通常采用引导文教学法、讨论法和思维导图教学法。充分发挥行动导向教学方法和传统教学方法的优势。

在每个学习情境的教学中设计任务单、分组单、信息单、资讯单、计划决策单、实施单、检查单、评价单和教学反馈单等教学表单，以便于具体实施教学。

基于科学发展观的评价观应该是以人为本的整体性评价观。符合现代职业教育理念的整体性评价方案有6个显著的整体思辨的特点：一是实践与理论结合；二是仿真与现场结合；三是结果与过程结合；四是动态与静态结合；五是专业成绩与能力评估结合；六是针对教育结构的考试与针对就业结构的考试结合[2]。

矿山机电专业应用数学课程应以整体性评价观为指导，建立合理、科学的整体性评价体系。评价既要关注学生数学学习的结果，也要关注他们数学学习的过程；既要关注学生数学学习的水平，也要关注他们在数学活动中所表现出来的情感态度的变化。在数学教育中，评价应建立多元化的目标，关注学生个性与潜能的发展。例如，过程性评价应关注对学生理解数学概念、数学思想等过程的评价，关注对学生数学地提出、分析、解决问题等过程的评价，以及在过程中表现出来的与人合作的态度、表达与交流的意识和探索的精神。要建立相应的过程评价内容和方法。

基于整体思考的应用数学课程评价方式由平时学习过程考核、期末卷面考试和综合任务考核三部分组成，遵循过程考核与终结考核相结合，理论考核和实践考核相结合的原则。学习过程考核占40%，期末卷面考核占30%，综合任务考核占30%。

学习过程考核主要是针对学生的出勤、作业、课堂提问情况以及小组讨论情况进行考核。可以采取教师、学生共同评价的方式，让学生参与到评价中来，体现公开、公平的原则，培养自我管理、自我调控的能力。

理论知识的考核采用过程考核中的平时作业和期末卷面考试的形式进行，主要考查学生对数学的基本知识和基本方法的掌握情况。

实践考核以综合任务考核的形式进行，主要针对学生完成数学建模任务的情况。实践考核指标应包括小组分工明确、有项目计划方案、小组活动记录、任务完成报告等。在考核时，以小组为单位进行报告或答辩，采取教师、学生共同评价的方式，让学生参与到评价中来，分享、学习他人的思想与创意。

三、结语

通过基于数学建模过程系统化的课程改革，高职数学课程实现了“学科体系”到“行动体系”的转变；从“内容中心”到“情境中心”的转变；从“传授知识”到“培养能力”的转变；从“传统教学”到“行动导向教学”的转变，这能使高职数学课程体现高职教育的类型特征，极大地提高了其教学效果。

基于数学建模过程系统化对高职数学课程进行改革，还是一个全新的尝试，困难和问题还很多。比如，教师的教学理念和教学能力还不能适应高职数学课程的这种转变；教学设施和条件也不能适应高职数学课程的这种转变；由于学时和学生基础的限制，每个学习情境中实际问题的选择还不能与专业深度融合，只能选择一些来源于日常生活且比较通俗易懂的问题等等。这些都需要进一步的深入思考和解决。

［1］贺楚雄.对高职数学课程定位与作用的重新认识［J］.武汉工程职业技术学院学报，2013（3）：87-89.

［2］姜大源.职业教育学研究新论［M］.北京：教育科学出版社，2007：23.

［3］姜大源.世界职教课程改革的基本走势及启示［J］.职业技术，2008（11）：4-10.

［4］涂荣豹，王光明，宁连华.新编数学教学论［M］.上海：华东师范大学出版社，2006.

［5］严中华.职业教育课程开发与实施［M］.北京：清华大学出版社，2009：188.

（责任编校：马余平）

The Course Development of Higher Vocational App lied M athem atics Based on the Systematized M athematical M odeling Process

HE Chu-xiong

（DepartmentofBasic Courses,JiangxiPolytechnic Collegeof Industryand Engineering,Pingxiang,Jiangxi337000）

According to the type characteristics of vocational education,This paper took the example of the course"Applied Mathematics of Mine Mechanical and Electrical Professional in Vocational Colleges"to study the developmentof higher vocationalmathematics course,which used the course development theory andmethod based on the systematized working process.This paper discussed the development of higher vocational mathematics course based on the systematized mathematical modeling process from several aspects,such as course development paradigm,course development ideas,teaching basic program,teaching method and course evaluation.

higher vocationalmathematics;mathematicalmodeling process;systematized working process; course development

G 712

A

1672-738X（2014）05-0066-04

2014-07-22

江西省高等学校教学改革研究省级一般课题“基于数学建模过程系统化的高职数学课程开发研究与实践”（JXJG-10-35-6）

贺楚雄(1972—)，男，江西萍乡人，数学副教授，工程硕士。主要研究方向：高职数学教育、应用数学。