地震作用下大跨度弦支穹顶结构的动力稳定分析

桂国庆，曾凡球，王玉娥

地震作用下大跨度弦支穹顶结构的动力稳定分析

*桂国庆1,2，曾凡球2，王玉娥1,3

(1.井冈山大学建筑工程学院，江西，吉安 343009；2.南昌大学建筑工程学院，江西，南昌 330031；3.江门市地震局，广东，江门 529000 )

根据B-R准则，结合结构时程响应曲线，判定弦支穹顶结构的动力稳定性，以跨度为120m的K8型弦支穹顶结构为研究对象，考虑不同矢跨比、不同预应力大小和不同地震波输入等参数的影响，对比分析其在水平、竖向和三向地震作用下极限承载力的不同及其变化规律。分析结果表明：大跨度弦支穹顶结构为了控制结构位移的需要，需施加较大的预应力，拉索引入较大预应力会增大与其相连的上部环向杆件的应力，使环向杆件在三维地震作用下更容易进入塑性；随着矢跨比增大，结构临界荷载增大但幅度很小。

大跨度；弦支穹顶；动力稳定；地震作用；矢跨比

弦支穹顶(suspend-dome)是由日本学者川口卫提出的一种新型复合空间结构体系，它运用整体张拉思想，将单层网壳和预应力拉索巧妙地结合起来，具有结构美观、省材、质量轻、刚度大、抗震性能好、造价低等优势[1]。一经提出，该结构很快就付诸工程应用，相关的研究工作也相继开展，然而大部分研究是集中在静力分析、稳定分析和结构形态分析等方面[2-4]，在其动力性能方面的研究较少。文献[5]对大跨弦支穹顶结构的自振特性进行了计算分析，考虑了不同参数对结构频率分布及振型特征的影响；陈志华等[6]利用环境激励法和锤击激励法对一联方型弦支穹顶结构进行了动力试验；邓华等[7]对罕遇地震下弦支穹顶的弹塑性动力响应进行了分析。由于弦支穹顶结构属于柔性支承体系，具有质量轻、柔性大、阻尼小的特点，在地震荷载作用下易产生较大的变形和振动，尤其随着结构的跨度不断增大，结构的动力稳定性问题也越来越突出。此外，以往对地震作用下弦支穹顶结构的动力稳定性分析大多限于较小跨度的情况[8]。因此，有必要深入系统地对大跨度弦支穹顶结构的抗震性能进行研究。

本文在以往研究的基础上，以跨度为120 m的K8型弦支穹顶结构为研究对象，采用通用有限元分析软件ANSYS，根据B-R准则[9-10]，结合时程响应分析，系统分析了多种因素对弦支穹顶结构动力稳定性的影响，其中包括不同矢跨比、不同预应力、不同地震波输入以及多维地震等，在此基础上探讨弦支穹顶结构的抗震问题，为将来工程实践提供理论依据。

1 模型建立及分析方法

1.1 计算模型及参数选取

分析模型为120 m大跨度K8型的弦支穹顶，结构模型如图1-图3所示[8]，上部单层网壳结构杆件之间的连接简化为刚接，采用BEAM188单元模拟；撑杆与上部单层网壳之间的连接简化为铰接，采用LINK8单元模拟，环索具有只拉不压的特性，采用LINK10单元模拟。弦支穹顶使用的基本材料有建筑型钢和索材两种，具体使用的材料参数见表1。

表1 弦支穹顶材料参数表

图1 上部网壳部分

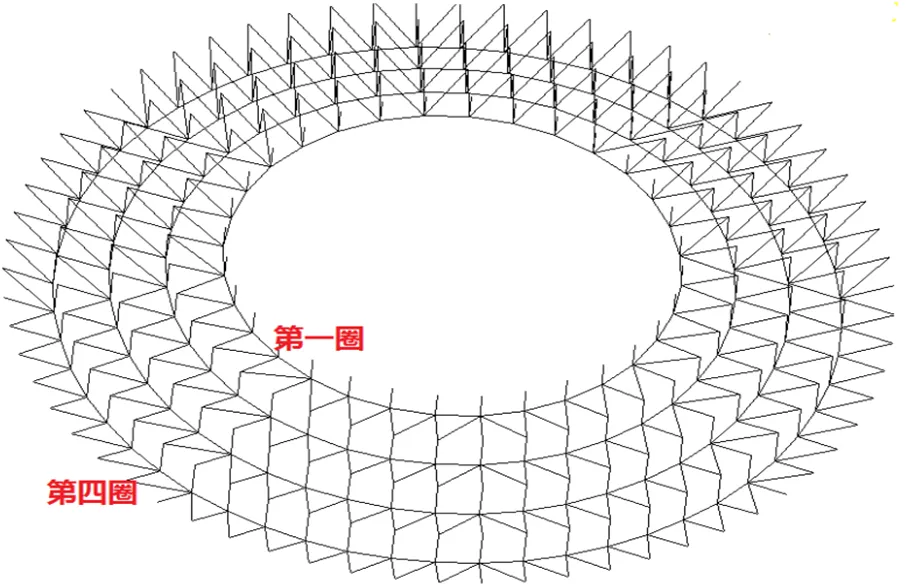
图2 张拉部分

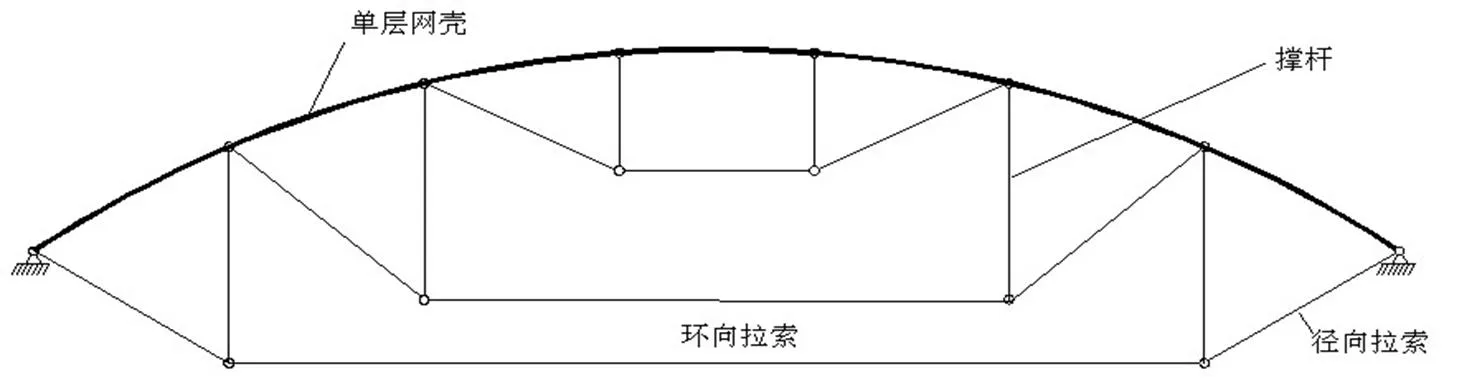
图3 弦支穹顶结构简图

下部预应力拉索由内到外隔圈布置，共布置4圈拉索，中心不布索。上部网壳采用P220×10的空心钢管；撑杆采用P219×7的钢管，截面面积为4662×10-6m2。具体拉索的尺寸见表2。

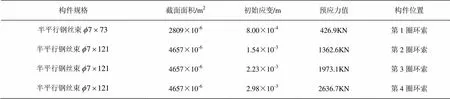
表2 拉索构件的几何参数

为了考察不同矢跨比和不同拉索预应力值对结构动力临界荷载的影响，将弦支穹顶结构的四道拉索预应力值分别乘以0.6和1.0的倍数（见表3），针对不同矢跨比和不同拉索预应力值研究结构的失稳过程及动力稳定性。表中，F/L和P分别表示结构矢跨比和预应力。

表3 工况变化与拉索预应力值

1.2 分析方法和分析步骤

分析结构地震反应时，采用的是一致地震输入法输入地震波，输入的地震波为三向等比例调幅的洛杉矶天然波和人工合成的地震波，输入持时为20s。阻尼假定为Rayleigh阻尼，阻尼比取0.02。计算过程中，采用通用有限元分析软件ANSYS，考虑材料和几何双重非线性。根据B-R准则，本文采用了如下判定弦支穹顶结构的动力失稳的方法：分别计算不同荷载峰值作用下的结构动力响应，并且绘制与荷载峰值相对应的位移曲线，在外荷载作用下，假设某非常小的荷载增量使得结构响应发生明显增大，此时曲线出现拐点，从而把此荷载峰值作为结构失稳的临界荷载点，并将此点的位移时程曲线作为判定结构动力稳定性的校核准则。

整个分析过程采用ANSYS自带的编程语言APDL和UIDL编程实现[8]，分析步骤如下：建立结构有限元模型并约束支座→读入地震波并进行求解→进入后处理。通过时程响应分析，记录结构的最大位移和其对应的最大地震加速度，将每次计算得到的加速度峰值和其对应的最大位移绘制成加速度幅值和位移响应曲线，当某非常小的荷载增量使得结构响应发生明显增大，此时曲线出现拐点，然后把此荷载峰值作为结构失稳的临界荷载。

2 地震作用下结构弹塑性动力稳定性分析

2.1 天然地震波作用下120m大跨度弦支穹顶结构的动力稳定性

通过分析，得到竖向地震作用下预应力值分别为0.6 P和1.0 P，矢跨比为0.125的弦支穹顶在不同的加速度峰值时对应的位移幅值，如图4示。根据判别方法，从图4中可看出0.6P的弦支穹顶的动力临界荷载为500 gal，1.0P的弦支穹顶的临界荷载为600 gal。竖向地震作用下矢跨比为0.166，预应力值分别为0.6 P和1.0 P的弦支穹顶在不同加速度峰值时对应的位移幅值见图5，同理可知0.6 P的弦支穹顶的动力临界荷载为800 gal，1.0 P的弦支穹顶的临界荷载为800 gal。

图6（a）、（b）分别是竖向地震作用下预应力值分别为0.6 P和1.0 P，矢跨比为0.125的弦支穹顶在不同的加速度峰值时对应的结构应力图。从图5中可以看出，结构在靠近中心第一圈的节点上失稳，这时杆件的最大应力是223 MPa和283 MPa，表明在失稳时没有杆件进入塑性，失稳由几何非线性控制。

图7（a）是竖向地震作用下预应力为0.6 P，矢跨比F/L=0.166的弦支穹顶在不同的加速度峰值时对应的结构应力图。从图7（a）可知，在失稳前，最大应力仅是143 MPa，杆件整体处于较低的应力水平，在失稳后，少数靠近支座的环向杆件，达到屈服状态。图7（b）是竖向地震作用下预应力为1.0 P，矢跨比为0.166的弦支穹顶在不同的加速度峰值时对应的结构应力图，在失稳前，杆件整体处于较低的应力水平；在失稳后，少数靠近支座的环向杆件，最大应力仅是263 MPa，应力较大但没有达到屈服应力。

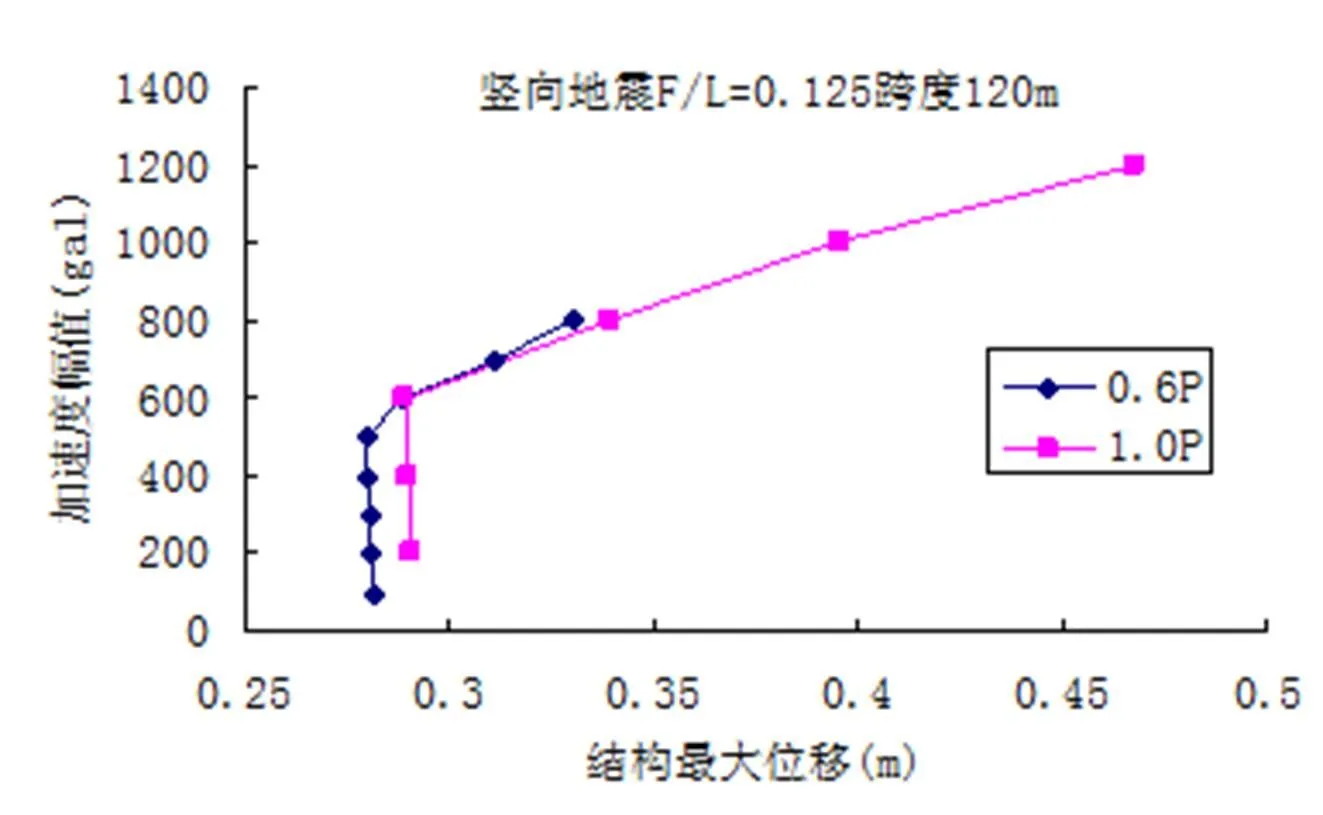
图4 竖向地震F/L=0.125结构加速度幅值-位移响应曲线

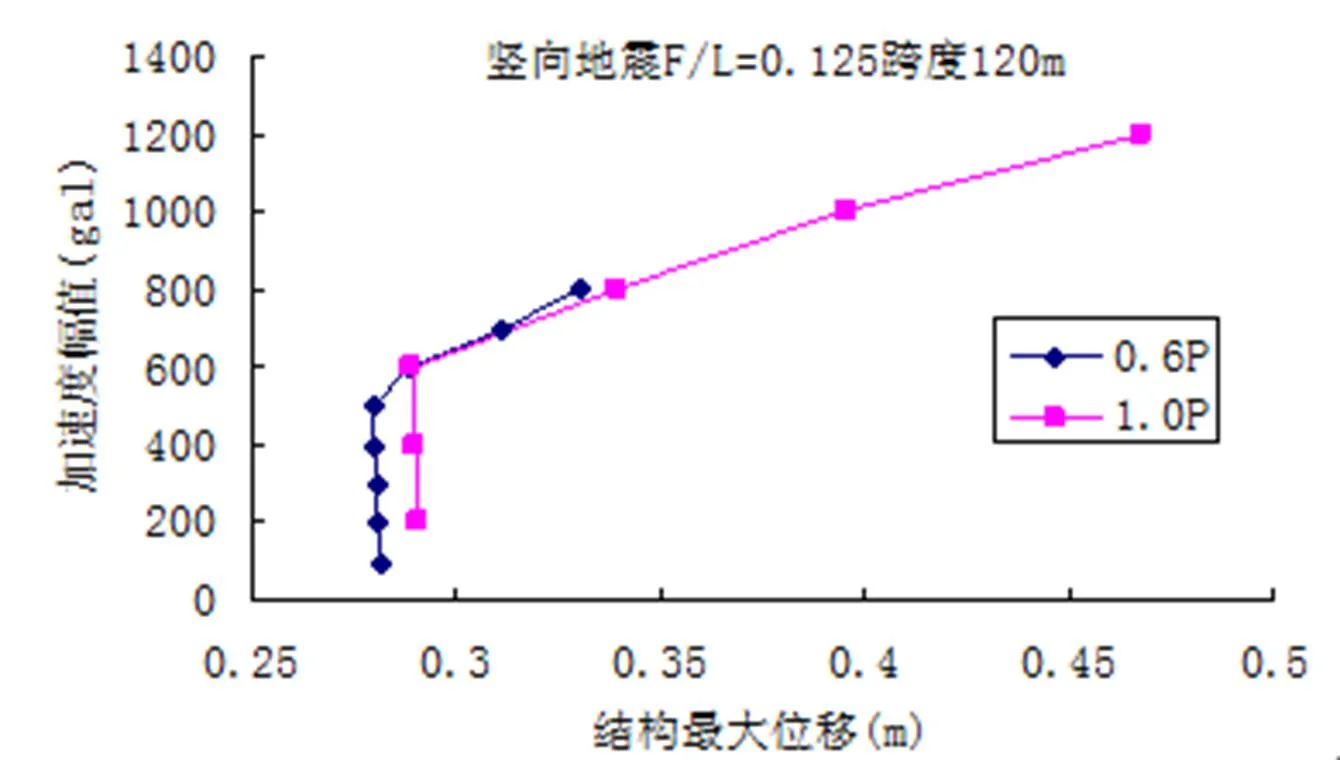
图5 竖向地震F/L=0.166结构加速度幅值-位移响应曲线

图6 竖向地震F/L=0.125不同的加速度峰值时对应的结构应力图

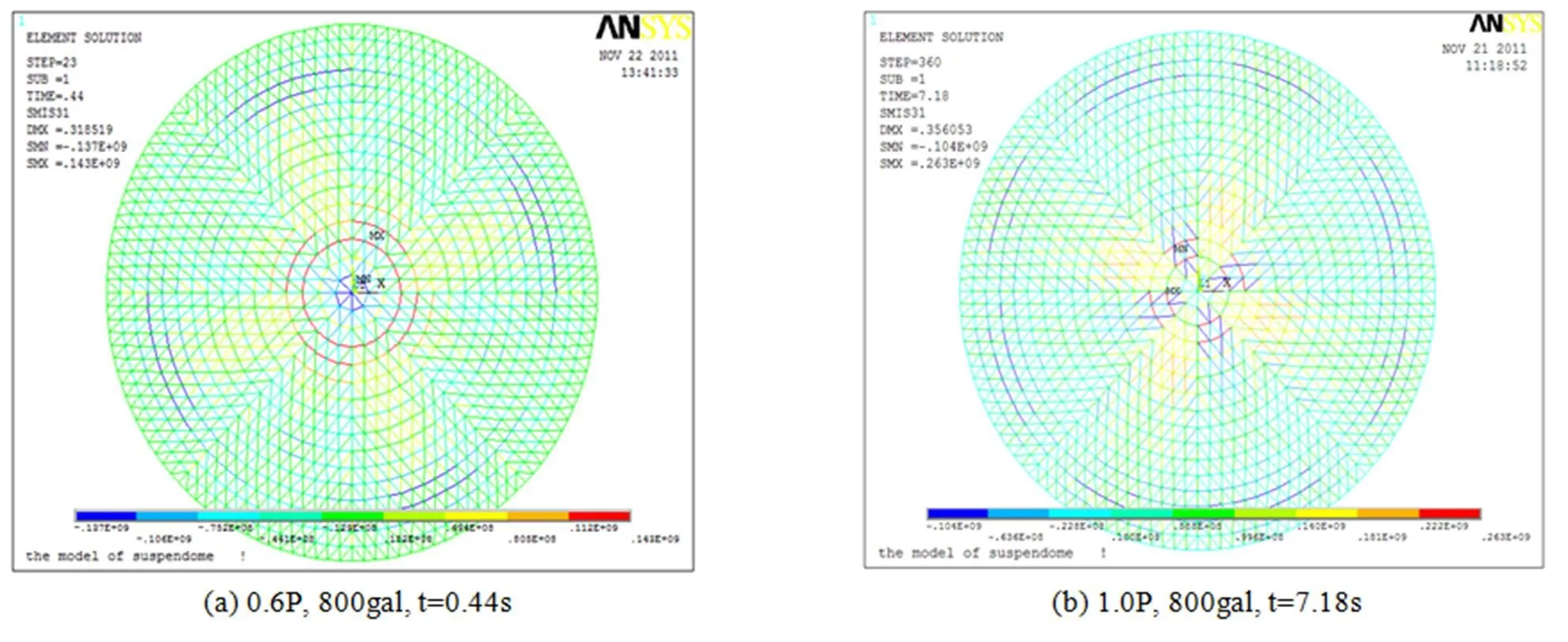
图7 竖向地震F/L=0.166不同的加速度峰值时对应的结构应力图

图8是水平地震作用下预应力值分别为0.6 P和1.0 P，矢跨比为0.125的弦支穹顶在不同加速度峰值时对应的位移幅值。根据判别方法，可知预应力值为0.6 P时弦支穹顶的动力临界荷载为400 gal，1.0 P时为500 gal。图9是水平地震作用下预应力值分别为0.6 P和1.0 P，矢跨比为0.166的弦支穹顶在不同加速度峰值时对应的位移幅值，同理可知预应力值为0.6 P时弦支穹顶的动力临界荷载为600 gal，1.0 P时为600 gal。图10（a）、（b）分别是水平地震作用下预应力值为0.6 P和1.0 P，矢跨比为0.125的弦支穹顶在不同加速度峰值时对应的结构应力图，从中可知结构的失稳点偏离了中心点，但没有超出中心未布置拉索的区域，在失稳前后，最大应力仅分别是117 MPa和189 MPa，杆件整体处于较低的应力水平。图11（a）、（b）分别是水平地震作用下预应力值为0.6 P和1.0 P，矢跨比为0.166的弦支穹顶在不同加速度峰值时对应的结构应力图，从中可知在失稳前后，最大应力仅分别是140 MPa和143 MPa，杆件整体处于较低的应力水平，其中靠近支座的几圈环向杆应力最大，这和靠近支座处结构下部布置的高强度拉索有关。

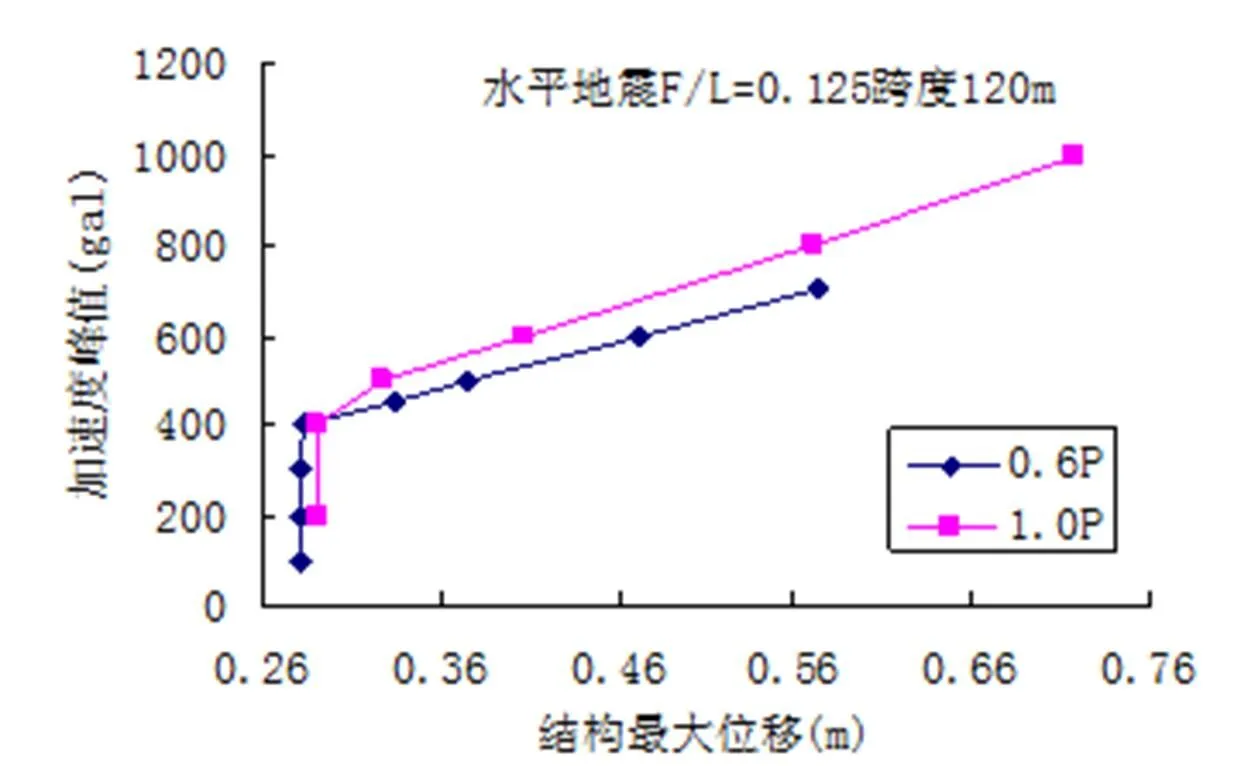
图8 水平地震F/L=0.125结构加速度幅值-位移响应曲线

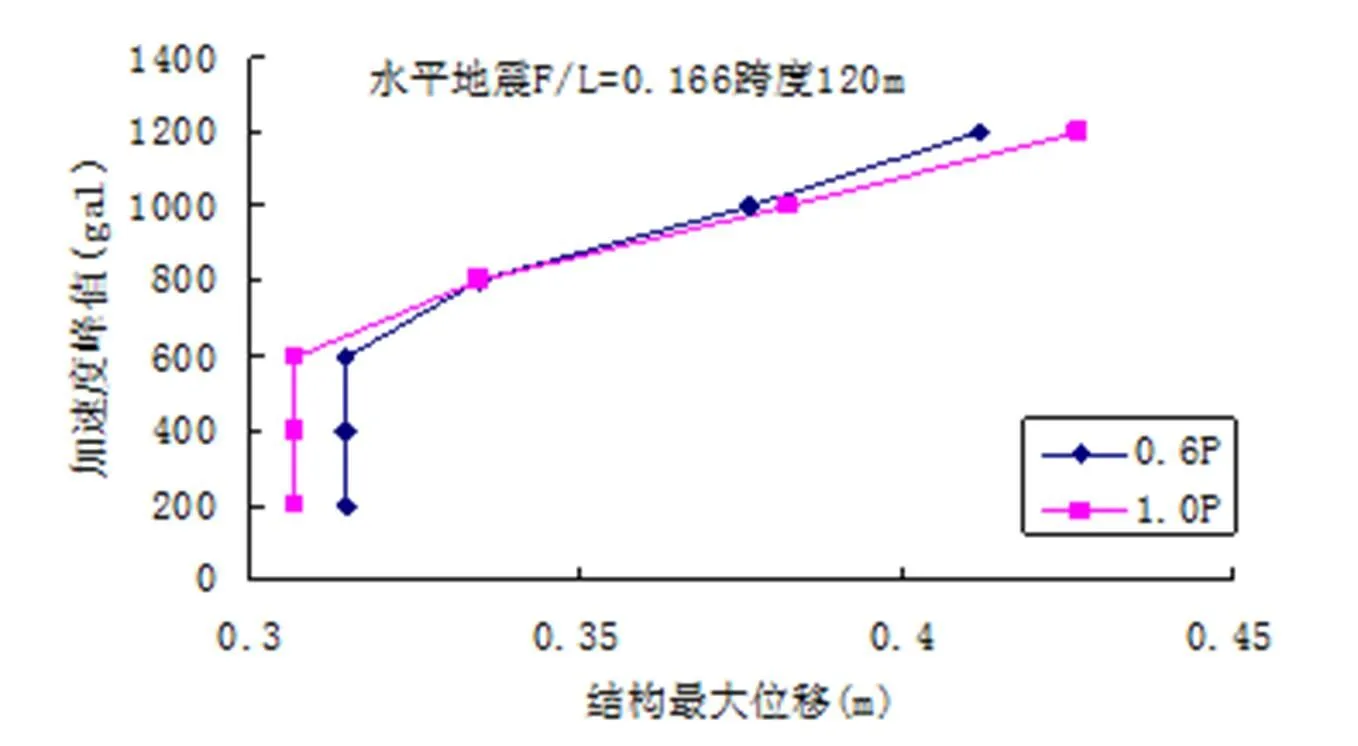
图9 水平地震F/L=0.166结构加速度幅值-位移响应曲线

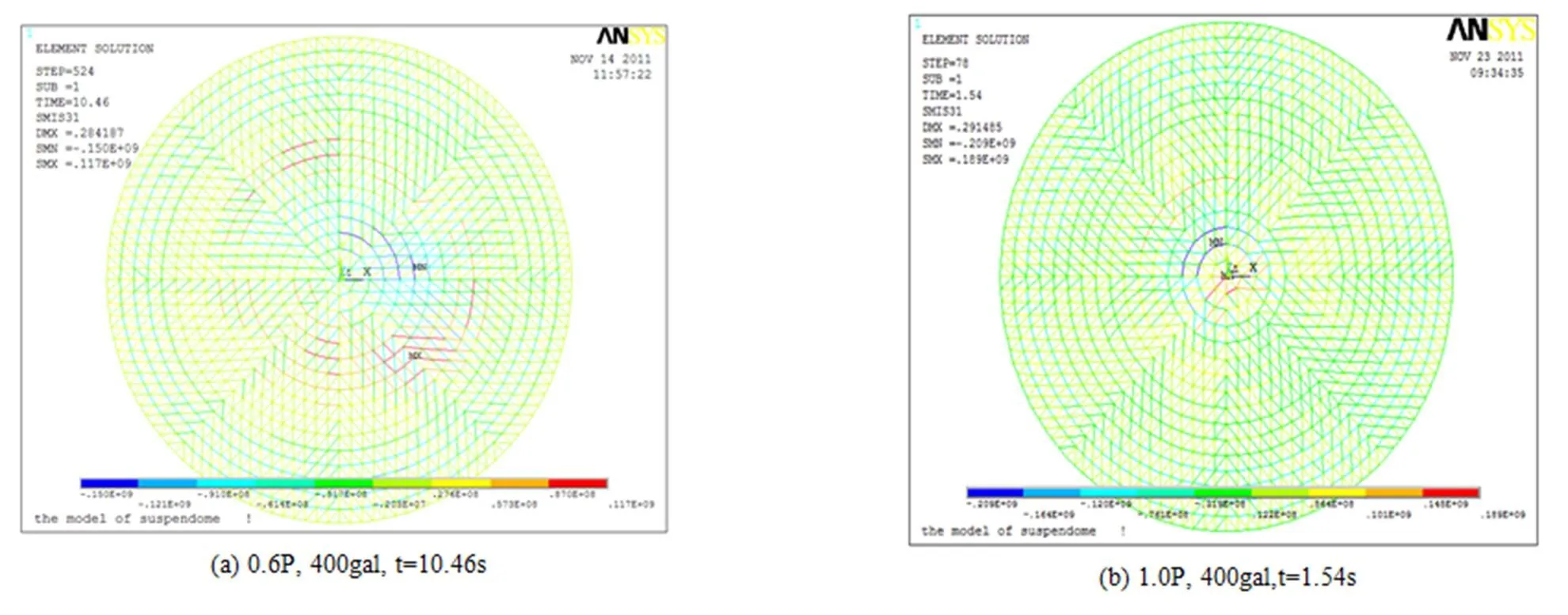
图10 水平地震F/L=0.125不同的加速度峰值时对应的结构应力图

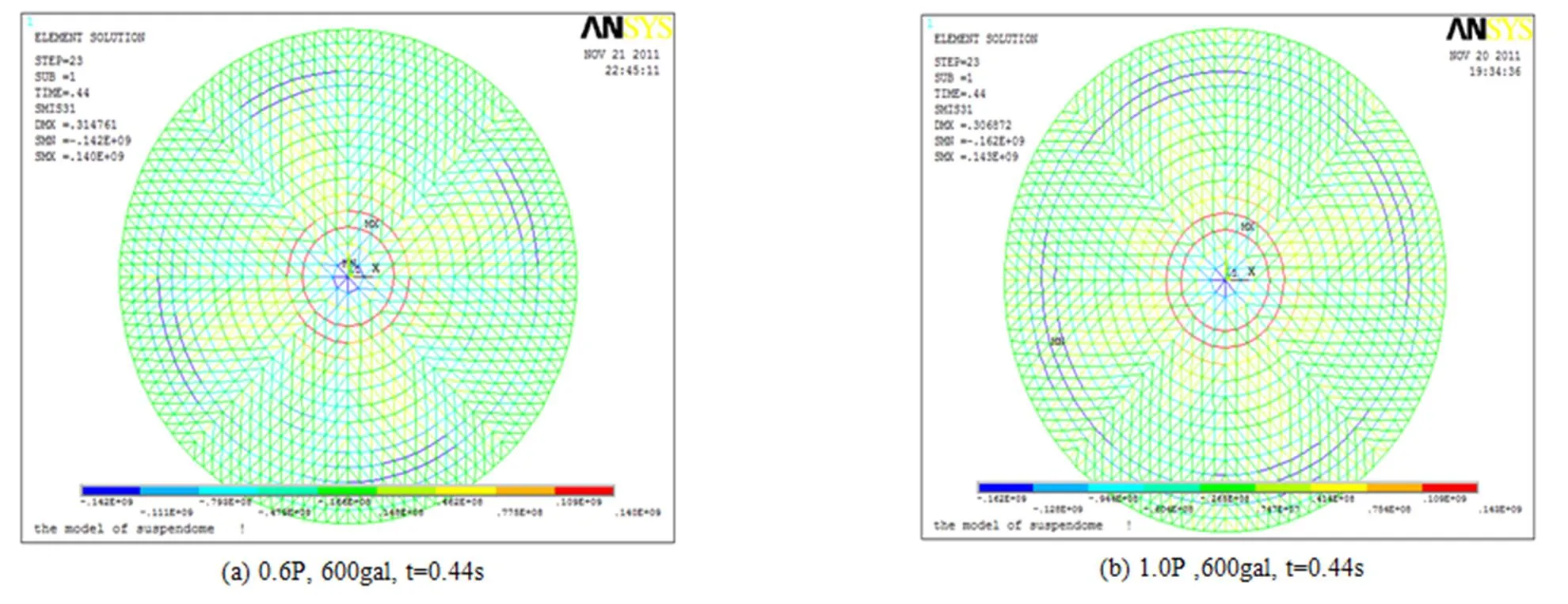
图11 水平地震F/L=0.166不同的加速度峰值时对应的结构应力图

图12是三向地震作用下预应力值分别为0.6 P和1.0 P，矢跨比为0.125的弦支穹顶在不同加速度峰值时对应的位移幅值。根据判别方法，可知预应力值为0.6 P时弦支穹顶的动力临界荷载为400gal，1.0 P时为400 gal。图13是三向地震作用下预应力值分别为0.6 P和1.0 P，矢跨比为0.166的弦支穹顶在不同加速度峰值时对应的位移幅值，同理可知预应力值为0.6 P时弦支穹顶的动力临界荷载为600 gal，1.0 P时为600 gal。图14（a）、（b）分别是三向地震作用下预应力值为0.6 P和1.0 P，矢跨比为0.125的弦支穹顶在不同加速度峰值时对应的结构应力图，从中可知在失稳前后，杆件整体处于较低的应力水平。图15（a）、（b）分别是三向地震作用下预应力值为0.6 P和1.0 P，矢跨比为0.166的弦支穹顶在不同的加速度峰值时对应的结构应力图，从中可知结构的失稳点偏离结构的正中心，但依然在未布置拉索的中心区域内，在失稳前后，杆件整体处于较低的应力水平，其中靠近支座的几圈环向杆应力最大，这和靠近支座处结构下部布置的高强度拉索有关。

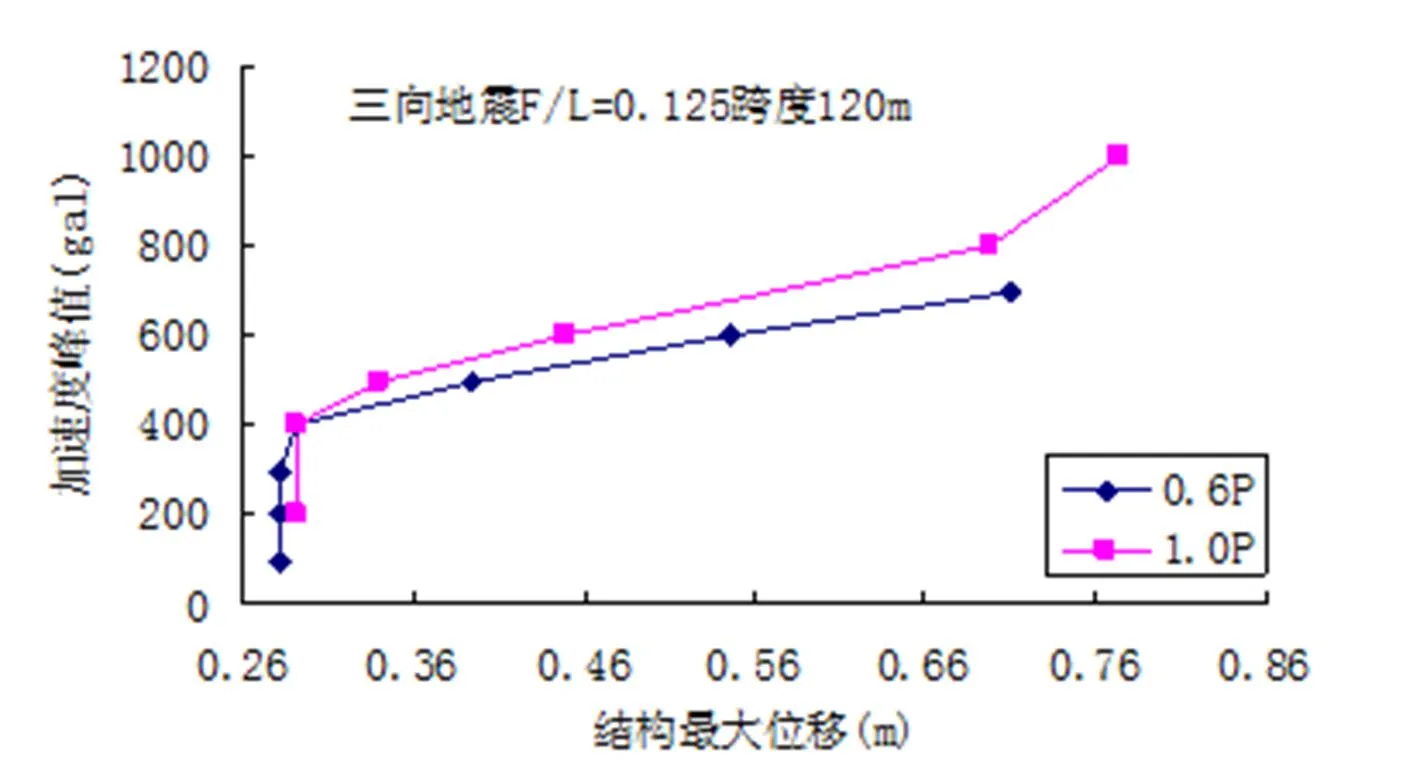
图12 三向地震F/L=0.125结构加速度幅值-位移响应曲线

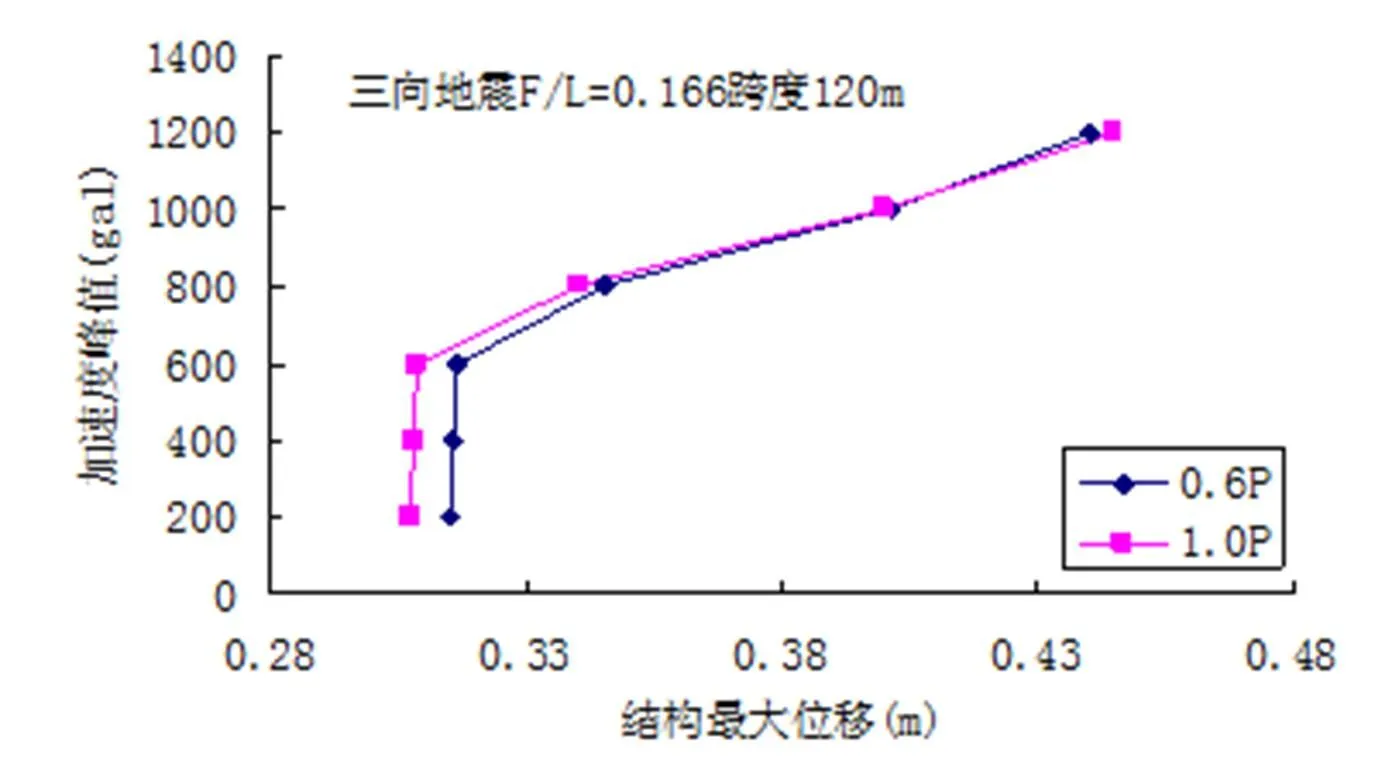
图13 三向地震F/L=0.166结构加速度幅值-位移响应曲线

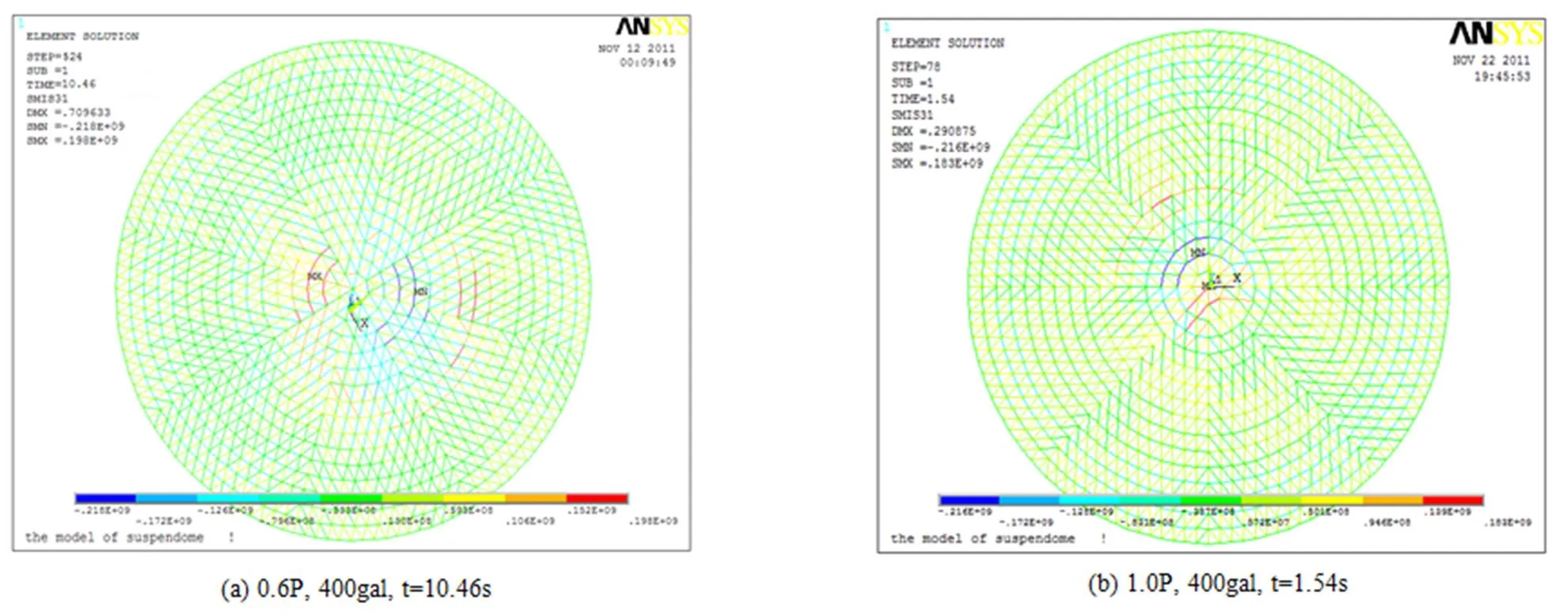
图14 三向地震F/L=0.125不同的加速度峰值时对应的结构应力图

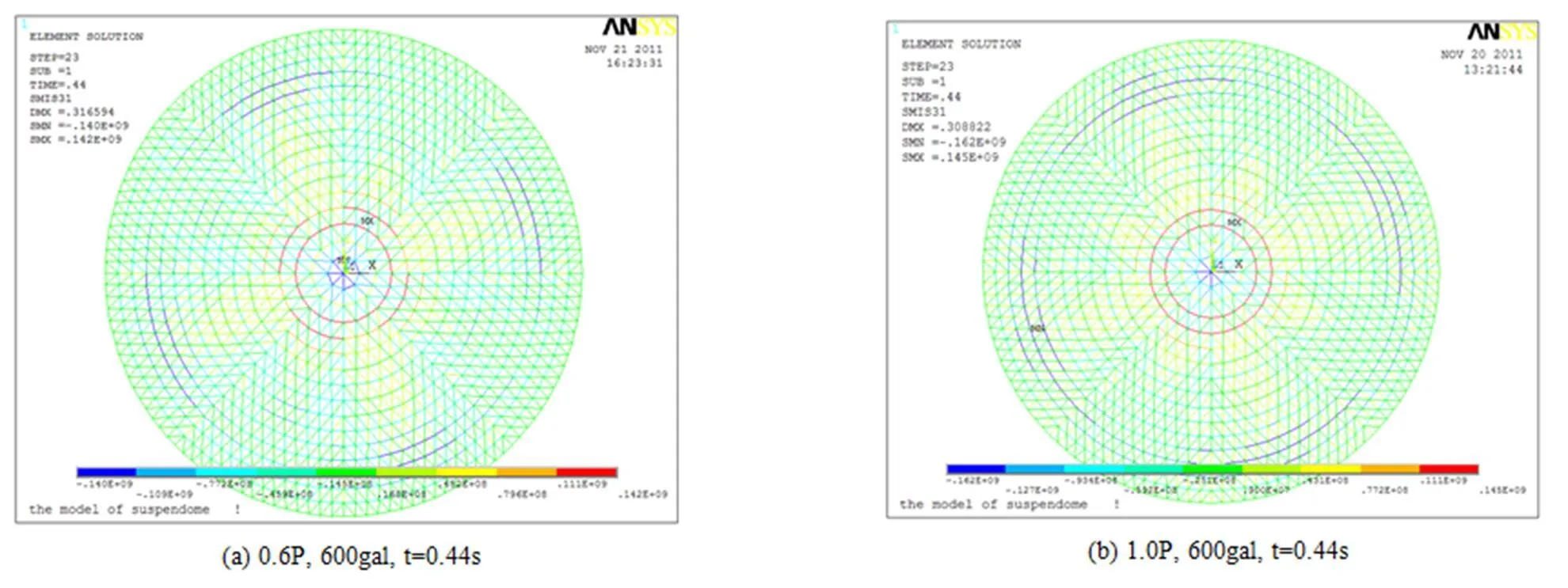
图15 三向地震F/L=0.166不同的加速度峰值时对应的结构应力图

2.2 人工地震波作用下120m大跨度弦支穹顶结构的动力稳定性

根据上述2.1的研究结果分析，由于其动力稳定性具有相似性，故仅以跨度为120 m，矢跨比为0.125，预应力值为0.6 P的弦支穹顶为例，分析其在水平、竖向、三向人工地震波作用下的动力稳定性。图16给出了其在不同加速度峰值时对应的位移幅值。根据判别方法，可知竖向地震作用下的弦支穹顶的动力临界荷载为500 gal，水平地震作用下的弦支穹顶的临界荷载为400 gal，三向地震作用下的弦支穹顶的临界荷载为400 gal。

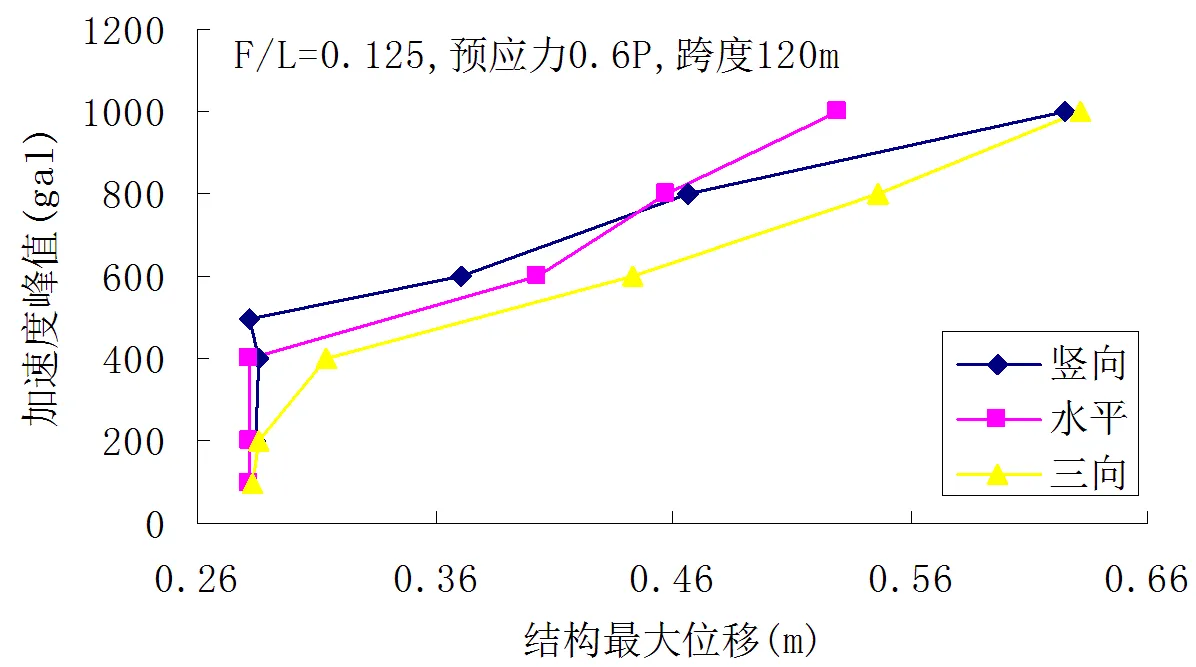
图16 多维人工地震波下结构加速度幅值-位移响应曲线

通过以上的分析计算，将跨度为120 m的弦支穹顶结构在不同地震波、不同矢跨比、不同预应力值的动力稳定临界荷载列入表4，从中可看出，无论是在人工波还是天然地震波作用下，120 m大跨度弦支穹顶在三向地震作用下结构的极限承载力普遍低于水平和竖向地震作用下结构的极限承载力，这说明地震作用是复杂多维的荷载作用，仅考虑单向单维是不够的；此外，结构的极限承载力随矢跨比的增加而增加，弦支穹顶结构的极限承载力在低矢跨比（0.125）时受预应力的影响明显，在高矢跨比时受预应力影响微弱。

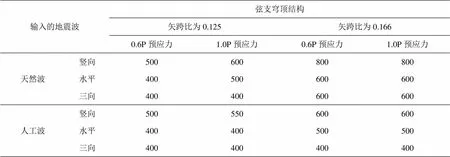
表4 弦支穹顶结构在不同地震波作用下稳定极限承载力的比较

3 结论

通过对120 m大跨度弦支穹顶结构分别在竖向、水平和三向地震作用下的动力稳定性能进行了一定规模的参数分析，得到以下结论：

1．无论施加的预应力值如何不同，结构的失稳只会发生在中心的“单层网壳”上。在竖向地震作用下，弦支穹顶在“单层网壳”正中心失稳；而在水平和三向地震作用中，弦支穹顶的失稳点会偏离正中心，但不会超过未布置拉索的中心区域。

2．弦支穹顶失稳时杆件的整体应力大于单层球面网壳的应力，拉索引入较大预应力会增大与其相连的上部环向杆件的应力，使环向杆件在三维地震作用下更容易进入塑性，在实际工程中，对于上述的应力较大处应格外重视。

3．预应力能够增加结构的极限承载能力，不同的预应力使极限承载力提高程度不呈线性关系，预应力值并不是越大越好。

4．随着矢跨比的增大，临界荷载增大，结构稳定性能提升，但矢跨比小的弦支穹顶的极限承载力提升幅度更大，更能发挥下部拉索的作用，并且不同的预应力作用下，增大的幅度也不同。

[1] 姚姝. 弦支穹顶结构的静力性能研究[D]. 哈尔滨：哈尔滨工业大学, 2006.

[2] 王泽强,秦杰,李国立,等.椭圆平面弦支穹顶静力性能研究[J]. 建筑结构, 2008, 38(2), 39-42.

[3] 葛家琪, 张国军, 王树,等. 2008奥运会羽毛球馆弦支穹顶结构整体稳定性能分析研究[J]. 建筑结构学报,2007, 28(6): 22-30.

[4] 陈志华, 李阳, 康文江. 联方型弦支穹顶研究[J]. 土木工程学报, 2005, 38(5): 34-40.

[5] 桂国庆, 周海峰. Kiewitt型弦支穹顶结构的自振特性研究[J].井冈山大学学报:自然科学版,2012,33(3): 78-82.

[6] 陈志华, 张立平, 李阳. 弦支穹顶结构实物动力特性研究[J].工程力学，2007,24 (3): 131-137.

[7] 王琼,邓华.罕遇地震下弦支穹顶的弹塑性动力响应分析[J]. 浙江大学学报:工学版, 2013, 47 (5): 1-7.

[8] 曾凡球. 大跨度弦支穹顶结构的静力及动力稳定性分析[D]. 南昌: 南昌大学, 2011.

[9] 郭海山,沈士钊.单层网壳结构动力稳定性分析方法[J].建筑结构学报, 2003, 24(3): 1-9.

[10] 沈世钊,支旭东.球面网壳结构在强震下的失效机理[J].土木工程学报,2005, 38(1): 11-20.

DYNAMIC STABILITY OF LARGE SPAN SUSPEND DOME UNDER SEISMIC EXCITATION

*GUI Guo-qing1,2，ZENG Fan-qiu2，WANG Yu-e1,3

(1. School of Architecture and Civil Engineering, Jinggangshan University, Ji’an, Jiangxi 343009, China;2. School of Architecture and Civil Engineering, Nanchang University, Nanchang , Jiangxi 330031, China；3. Seismological Bureau of Jiangmen City, Jiangmen, Guangdong 529000, China)

Based on B-R criteria combined the method and time history response curves, the dynamic stability of suspend domes was judged. The dynamic stabilities of suspend dome of 120m span under vertical, horizontal and three-dimensional seismic excitation were calculated respectively taken into account the different pre-stress values and the different rise-span ratios. The results show that the large span suspend dome structure needs to exert greater pre-stress to control displacement and the introduction of high intensity cables increase the stress of circumferential bars which make circumferential bars more easily reach plasticity, and the critical dynamic load of the structure increases with the increase of the ratio of rise to span while the increasing magnitude is small.

large span; suspend dome; dynamic stability; seismic excitation; ratio of rise to span

1674-8085(2014)01-0076-08

TU311.3, TU393.3

A

10.3969/j.issn.1674-8085.2014.01.016

2013-11-26；

2013-12-16

江西省自然科学基金项目（20132BAB202006），江西省教育厅科学技术研究重点项目（GJJ10025）

*桂国庆(1966-)，男，江西东乡人，教授，博士，主要从事结构工程、计算力学及振动理论研究(E-mail:gqgui2011@163.com);

曾凡球(1987-)，男，江西南昌人，硕士，主要从事结构工程、结构抗震方面的研究(E-mail: ballzeng1987@126.com);

王玉娥(1982-)，女，江西临川人，讲师，硕士，主要从事结构工程、结构抗震方面的研究(E-mail: wangyue6202@sohu.com).