基于SSOR预条件技术的快速相位解缠算法

刘志伟，张月园，张晓燕，何 姗，刘颖婷



基于SSOR预条件技术的快速相位解缠算法

*刘志伟1,2，张月园1，张晓燕1,2，何 姗1，刘颖婷1

(1. 华东交通大学信息工程学院，江西，南昌 330013；2. 毫米波国家重点实验室，江苏，南京 210096）

相位解缠是合成孔径雷达干涉测量中的一个关键步骤和研究热点。在众多的解缠算法中，最小二乘相位解缠算法以其优良的稳定性受到人们的关注。该方法的核心思想是将相位解缠问题转化为通过迭代方法求解大型线性方程组。然而，传统的迭代方法存在收敛缓慢，耗时过长的缺点。针对这一问题，本文提出了一种利用对称超松弛预条件技术加速相位解缠的新方法。数值仿真实验表明，与传统方法相比，该方法可以在精确恢复真实相位的前提下，大大提高相位解缠的效率。

相位解缠；干涉合成孔径雷达；广义最小余量法；对称超松弛预条件

干涉合成孔径雷达(Interferometric Synthetic Aperture Radar, InSAR)是利用合成孔径雷达复图像的相位数据来获取地面目标三维空间信息和变化信息的一项技术[1]。InSAR通过两副天线同时观测(双天线模式)或两次近平行的观测(重复轨道模式)获取地面同一场景的信息，并利用合成孔径雷达成像技术获取相应的两幅复图像[2]。由于目标与两天线位置的几何关系不同，使得在两幅复图像之间存在相位差。于是，我们便可以从两幅复图像共轭相乘后获得的干涉纹图出发，反演出场景中的高程信息。

在利用InSAR测高的实现过程中，由于受到三角函数主值的影响，使得干涉图中的相位不再是真实的相位差，而是被周期折叠后位于[-π, π]之间的相位主值[3]，它与真实的相位差之间存在着2kπ差别，为整数。为了能够精确恢复场景的高程，必须由干涉图中的相位主值恢复出真实相位差，这一过程便被称为相位解缠[4]。相位解缠是InSAR处理中的关键步骤，其准确程度将直接决定数字高程图(DEM)和地表形变探测的精度。

当前，相位解缠的方法主要分为两大类: 路径追踪法和最小二乘法[5]。其中，基于最小二乘的相位解缠算法是一种具备良好稳定性的全局最优方法，它将相位解缠问题转化为通过求解离散的泊松方程，寻找缠绕相位的离散偏导数与解缠相位的偏导数整体偏差最小的解。针对这类大型稀疏矩阵方程，通常采用迭代算法加以求解，如Gauss-Seidel，GMRES迭代法等[6]。然而，由于传统的迭代方法存在不稳定和收敛速度慢等缺点，使得相位解缠的求解时间往往过长，求解精度也难以保证。为了解决这一难题，本文将预条件思想[7-8]引入到基于最小二乘法的相位解缠过程中。通过理论分析及数值仿真实验验证，预条件方法可以在不增加额外计算量的基础上，加速迭代算法的收敛，从而显著提高相位解缠的效率，减少计算时间。

1 最小二乘相位解缠绕

基于理想情况下解缠相位梯度等于缠绕相位梯度的假设，相位解缠可以看成是一个优化问题。最小二乘法是一种广泛使用的优化方法。它的主要思想是基于解缠相位和缠绕相位之差的平方和最小准则，其目标函数为：

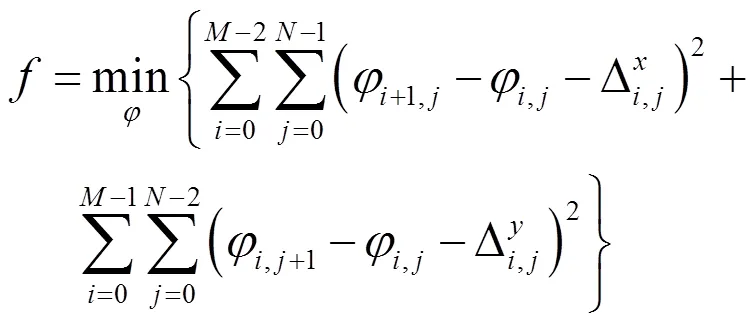
其中，φ,j为解缠后相位的估值，且

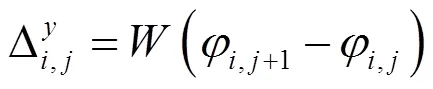
代表缠绕操作，目的是对缠绕相位差分进行加或减2π, 从而确保Δ,j和Δ,j位于[-,]之间。

对每一个像素(,)，方程(1)可改为如下的离散泊松方程

(φ+1,j- 2φ,j+φ-1,j) + (φ,j+1- 2φ,j+φ,j-1) =ρ,j(2)

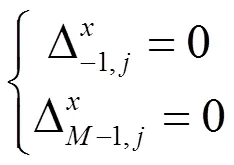
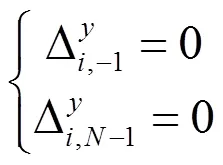
由上面的分析可以看出，最小二乘的相位解缠算法等效于求解纽曼边界下的泊松方程，它可以表示为一个未知量为(=×) 的稀疏线性方程组：

Aφ = ρ (3)

其中，A是一个稀疏矩阵，φ和ρ分别代表φ,j及ρ,j的一维列向量。

2 基于预条件技术的相位解缠绕算法

最小二乘算法将相位解缠转化为等价的泊松方程之后，由于生成的大型稀疏线性方程组阶数通常很高，使得直接求解需要大量的计算资源和存储空间。因此，通常需要采用迭代方法对(3)式进行求解。求解稀疏线性方程组的迭代法[6]通常采用超松弛(SOR)和Krylov子空间方法等。前者一般称为静态迭代方法，而后者称为非静态迭代方法，采用何种方法求解，视具体情况而定。

对于静态迭代方法，以Gauss-Seidel迭代为例，首先将(3)式中的阵列φ,j初始化为0，然后采用(4)式的迭代形式进行计算，直至收敛。

φ,j= 0.25 × (φ+1,j+φ-1,j+φ,j+1+φ,j-1-ρ,j) (4)

实践证明，静态迭代方法尽管数学形式比较优美，但对低频误差分量的消除能力却很弱，从而导致了很低的收敛速度。对于求解性态较差的线性系统，往往采用Krylov子空间方法，其中最典型的代表是采用广义最小余量法(GMRES)求解线性系统。该方法于1986年由Saad和Schultz提出[6]，只需要直接的矩阵矢量乘(Matrix Vector Product: MVP)的信息就可以顺利进行迭代，获得满足收敛精度的解，同时还具有稳定的收敛速度，因此可应用于一般的非Hermitian矩阵方程的求解。

假定待求解的矩阵方程为Aφ = ρ，对于任意给定的一个初始近似解φ0，其相应的余量为r0= ρ – Aφ0。GMRES的迭代过程通过构造Krylov子空间span{r0, Ar0, …, A-1r0}的一组正交规范基，并在此空间内获得对精确解的逼近，代表Krylov子空间的维数。GMRES算法具有稳定性好，操作简单的特点，然而，对于条件数大，即性态很差的系数矩阵，GMRES迭代算法也会出现收敛十分缓慢的现象。这是因为从本质上来说，迭代算法的收敛特性是由待求解系数矩阵的性态，即系数矩阵的条件数决定的，条件数较小时矩阵方程收敛较快，反之亦然。由此，我们不难想到，如果在迭代开始之前，利用另一个非奇异矩阵M对系数矩阵A进行预处理，使得预处理后的矩阵M-1A的特征值分布在几个相对集中的区域，那么便可使预条件后的矩阵方程相比原方程具有更加良好的性态，即其特征谱是聚集的，从而有利于加速迭代算法的求解。

因此，采用预条件技术后，对方程Aφ = ρ的求解转化为求解方程

M-1Aφ = M-1ρ (5)

从这里可以看出，预处理后的线性系统是否比原系统更易于求解，取决于是否构造一个高效的预条件算子。预条件算子的构造一般需要遵循以下基本原则[6,8]

1) M应该是A或者A-1在某种意义下的一个良好的近似；

2) 构造预条件矩阵M本身的计算复杂度和内存消耗要小；

3) 预条件操作的施加，即对任意一个矢量x，M-1x或Mx的计算量要小。

本文采用的对称超松弛预条件(SSOR)来加速线性系统的求解，它完全满足三条基本原则，相应预条件矩阵定义为[7]：

M = (D +E)D-1(D +F) (6)

其中，D、E、F分别表示系数矩阵A的对角阵、严格下三角阵以及严格上三角阵，为松弛因子，通常取值范围为[0, 2]。我们注意到，由于SSOR预条件算子的分解因子是直接从系数矩阵A中抽取的，因此构造代价极小，同时还可以有效避免预条件算子构造过程中的不稳定现象[6]。

3 数值算例

为了验证结合预条件技术的迭代方法在相位解缠中的效果，针对典型的高斯山相位，我们进行了相应的数值仿真实验。图1和图4分别为单个和两个相邻的高斯山相位，图2和图5为缠绕后的单个和两个相邻的高斯山相位，即缠绕相位。由图2和图5可以看出，缠绕相位为真实相位的主值，限于[-,]范围之内。

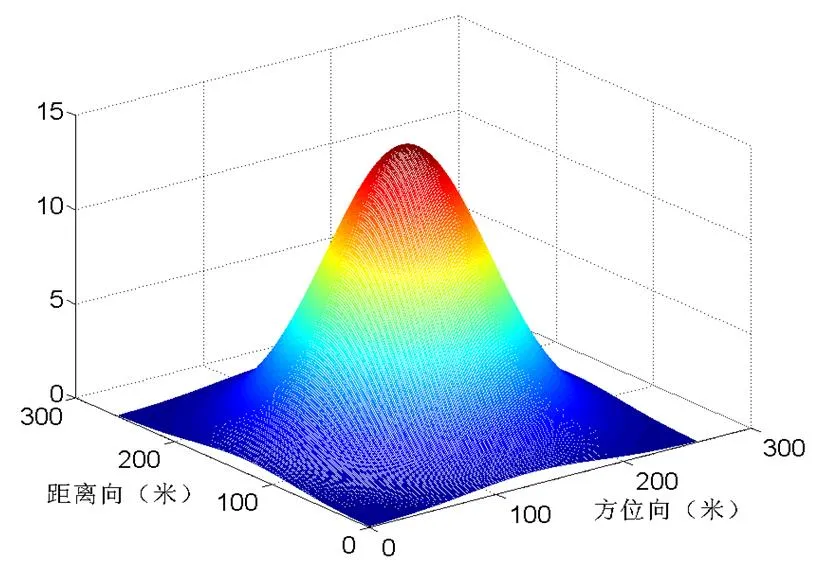
图1 真实的单个高斯山相位

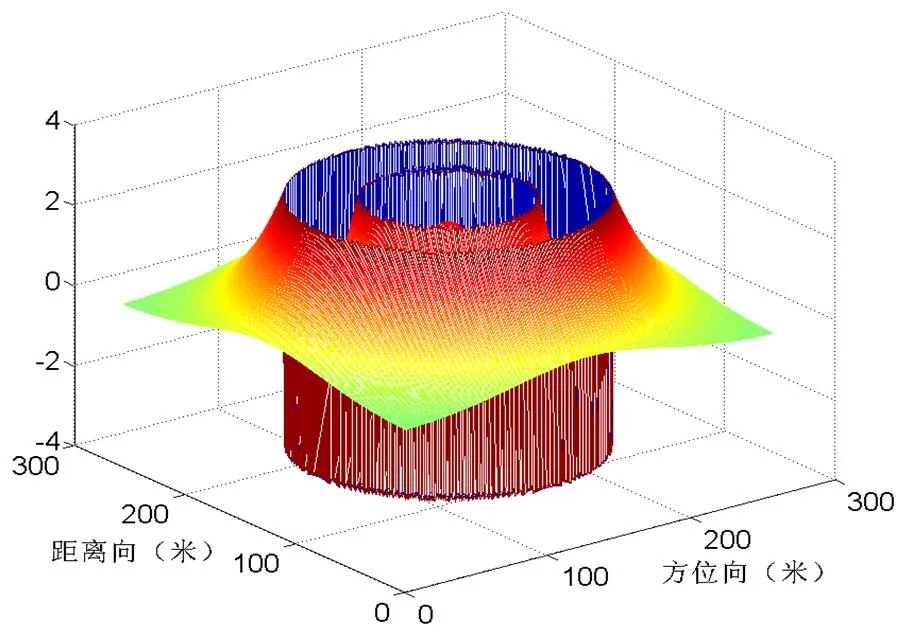
图2 单个高斯山缠绕相位

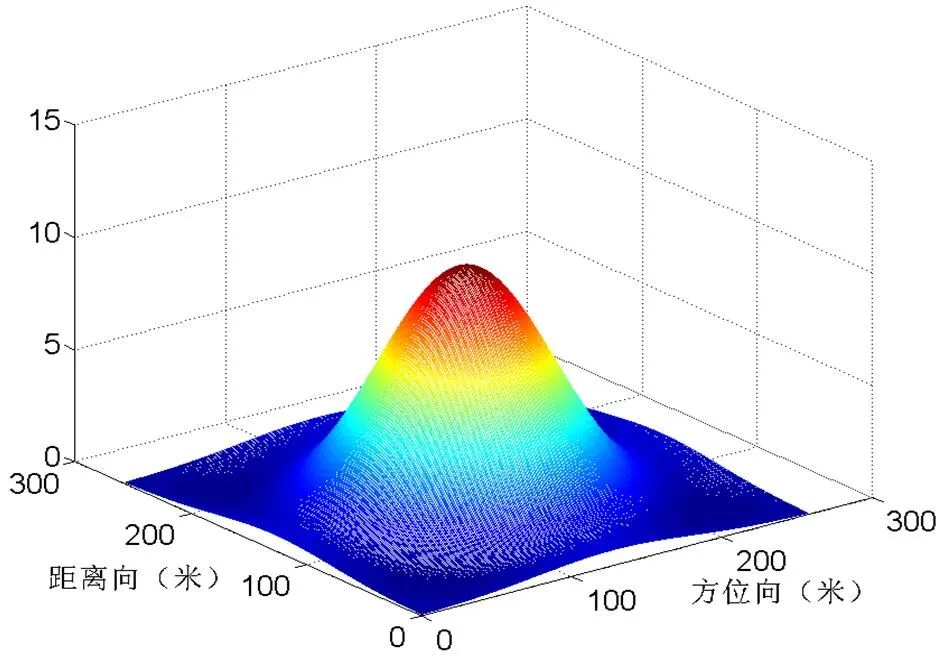
图3 单个高斯山解缠后的相位

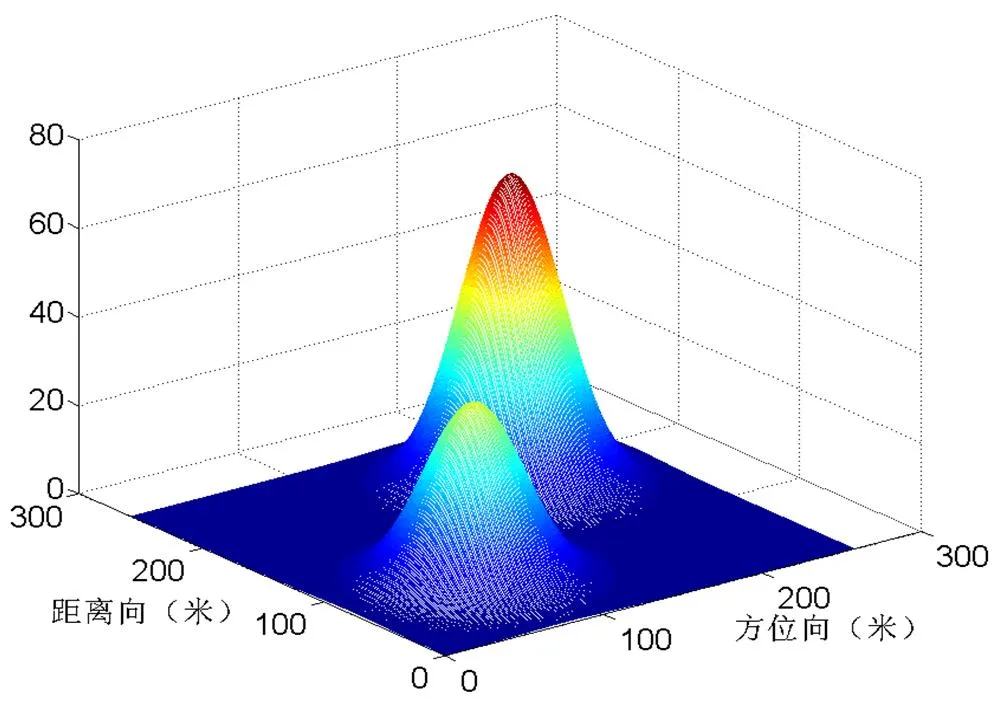
图4 两个相邻的高斯山相位

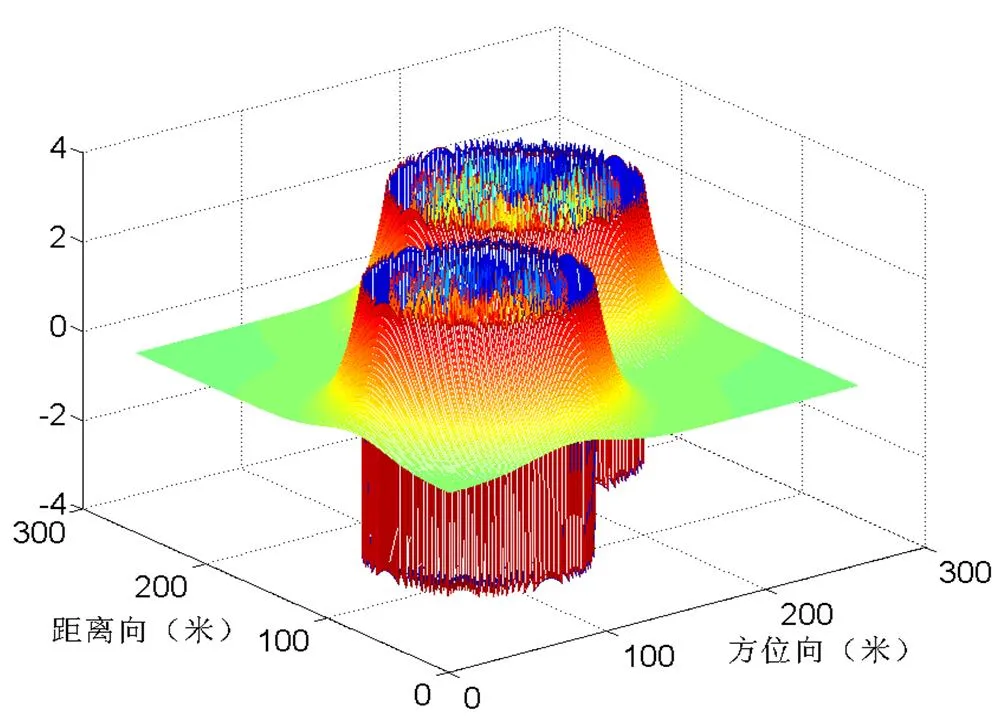
图5 两个相邻高斯山的缠绕相位

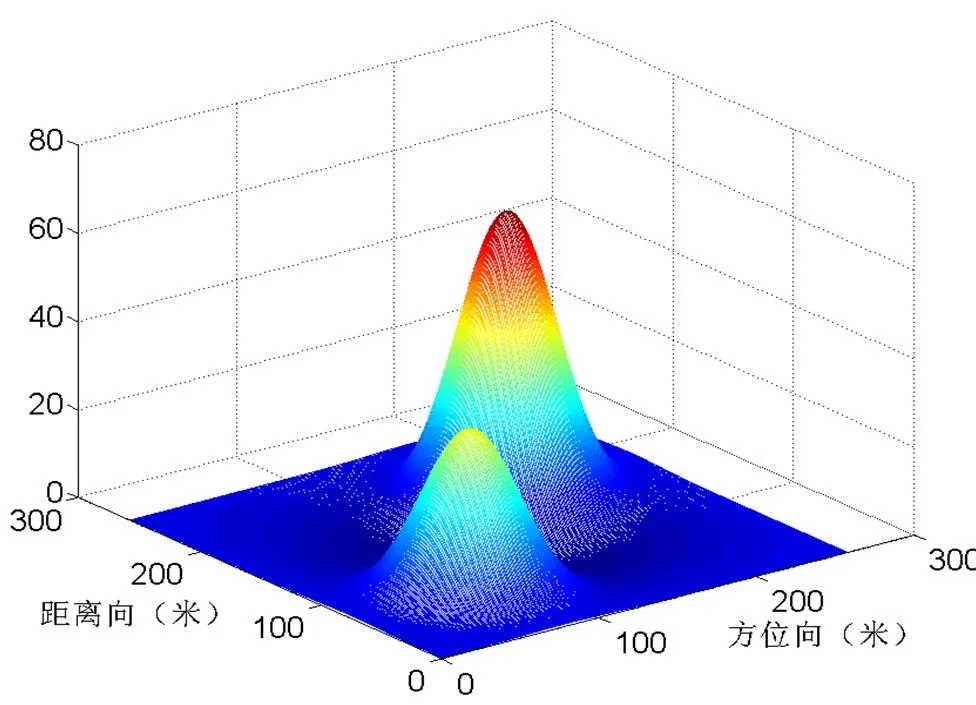
图6 两个相邻高斯山解缠后的相位

图3和图6则分别反映了采用SSOR预条件技术之后，GMRES迭代方法进行相位解缠后的输出结果。通过将图3与图1，图6与图4分别进行比较后不难看出，SSOR-GMRES算法可以准确的由缠绕相位恢复出真实相位，精确完成相位解缠的操作。

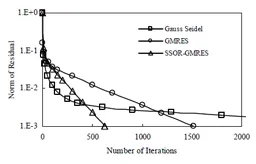
图7 单个高斯山两种解缠算法的迭代步数比较

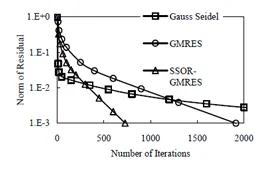
图8 两个相邻高斯山两种解缠算法的迭代步数比较

为了进一步说明SSOR-GMRES算法在处理相位解缠问题上的有效性，我们分别采用SSOR-GMRES算法和传统的Gauss-Seidel迭代法对图2和图4所示的缠绕高斯山相位进行相位解缠，并在统一的收敛精度(10-3)的前提下，将不同算法的迭代求解步数进行了比较，如图7、图8和表1所示。由图表可以看出，SSOR-GMRES算法所需的收敛步数远远小于传统的Gauss-Seidel迭代法，从而证明了预条件技术可用来加速干涉SAR中的相位解缠，具有较大的实用价值和现实意义。

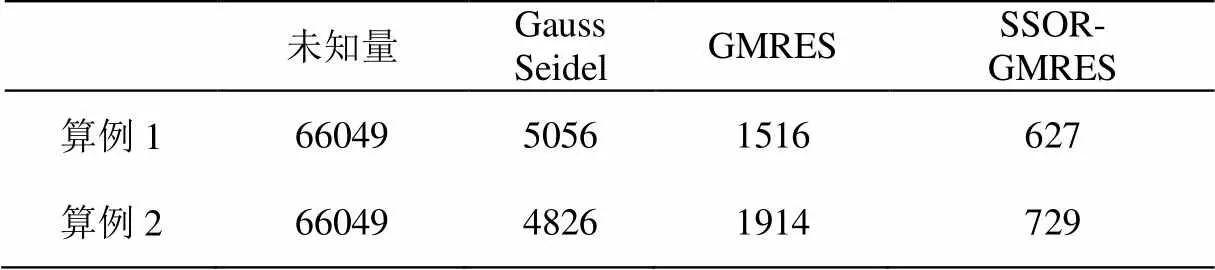
表1 两种解缠算法的迭代步数比较(迭代精度10-3)

4 结论

相位解缠是InSAR数据处理流程中的一个关键步骤，同时也是一个难点，因此，对解缠算法的研究具有重要意义。本文提出了一种将预条件技术与迭代法相结合，快速求解相位解缠问题的新方法，并就该方法的数学原理及实现手段进行了详细阐述。理论分析及数值算例结果表明，预条件技术是一种加速迭代收敛的有效方法, 在求解相位解缠问题时具有收敛速度快、计算效率高、解缠精度高等优点，具有较大的实用价值和广泛的应用前景。

[1] 保铮. 雷达成像技术[M]. 北京:电子工业出版社,2005.

[2] 王磊. 干涉合成孔径雷达信号处理的研究[D]. 北京: 中国科学院电子学研究所, 2001.

[3] Loffeld O, Nies H, Knedlik S, et al. Phase Unwrapping for SAR Interferometry - A data fusion approach by Kalman Filtering[J]. IEEE Trans. Geosicence and Remote Sensing, 2008, 46(1): 47-58.

[4] Goldstein R M, Zebker H A , Werner C. Satellite radar interferometry: Two-dimension phase unwrapping[J]. Radio Science, 1998, 23(4): 713-720.

[5] Bao M, Kwoh L K, Singh K. A improved least-squares method for INSAR phase unwrapping[C]. IEEE International symposium on Geoscience and remote sensing, 1998: 62-64.

[6] Yousef Saad. Iterative methods for sparse linear systems[M]. PWS Publishing Company, 1996

[7] Chen R S, Edward K N, Yung C H, et al. Application of SSOR preconditioned conjugate gradient algorithm to edge-FEM for 3-dimensional full wave Electromagnetic boundary value problems[J]. IEEE Trans. Microwave Theory and Techniques, 2002, 50(4):1165 -1172.

[8] 芮平亮. 电磁散射分析中的快速迭代求解技术[D]. 南京：南京理工大学, 2007.

PHASE UNWRAPPING BY MEANS OF PRECONDITIONING TECHNIQUE FOR INTERFEROMETRIC SAR BASED ON SSOR PRECONDITIONER Preconditioning technique for Interferometric SAR

*LIU Zhi-wei, ZHANG Yue-yuan, ZHANG Xiao-yan, HE Shan, LIU Ying-ting

(1. School of Information Engineering, East China Jiaotong University, Nanchang, Jiangxi 330013, China;2. State Key Laboratory of Millimeter Wave, Southeast University, Nanjing, Jiangsu 210096, China)

To solve the two-dimensional phase unwrapping problem, least square phase unwrapping is a robust approach, which is equivalent to the solution of a large sparse linear equation based on the iterative method. However, the convergence rate of the iterative method is usually very slow. To efficiently solve these linear systems arising from phase unwrapping problems, we propose the preconditioning technique. Numerical results demonstrate that the present method can reduce the number of iterations significantly, when no additional computing time is required to construct the preconditioning matrix.

phase unwrapping; interferometric synthetic aperture radar (InSAR); general minimal residual method (GMRES); SSOR preconditioner

1674-8085(2014)01-0046-05

O175.2

A

10.3969/j.issn.1674-8085.2014.01.010

2013-09-10；

2013-10-12

国家自然科学基金项目(61261005)；毫米波国家重点实验室开放课题(K201326)；江西省科技厅青年基金项目 (20122BAB211018)；华东交通大学校立科研课题 (11XX01)

*刘志伟(1982-)，男，江西南昌人，讲师，博士，主要从事计算电磁学研究(E-mail: zwliu1982@hotmail.com);

张月园(1981-)，女，浙江金华人，讲师，硕士，主要从事计算机应用技术研究(E-mail: aney0360_cn@sina.com);

张晓燕(1979-)，女，云南楚雄人，副教授，博士，主要从事计算电磁学研究(E-mail: xy_zhang3129@sina.com);

何 姗(1989-)，女，安徽安庆人，硕士生，主要从事计算电磁学研究(E-mail: lucky-shan@163.com);

刘颖婷(1988-)，女，湖南冷水江人，硕士生，主要从事计算电磁学研究(E-mail: yingtingmm@163.com).